基于分形理论的通信个体电台细微特征提取技术研究*

谭 薇，严丽娜，姚 晖，刘锐鹏

（1.国防科技大学信息通信学院试验训练基地，陕西 西安 710106；2.西安工业大学，陕西 西安 710021）

0 引 言

通信电台技术参数的特征差异较小，所以通信电台个体识别须利用细微特征进行识别。细微特征通常称为通信电台的“指纹”，是由于电台在制造过程中的各种随机因素造成的个体差异。这些差异表现出来的特征是通信信号具有细微的差异，且表现出一定的稳定性和规律性。因此，可通过提取通信信号的指纹特征进行分析匹配，从而识别相同制式的通信电台个体。

通过分析提取电台通信信号的细微特征，不仅能实现对通信信号源的分析、识别、监测和确定干扰对象，而且可以为识别通信电台个体、其所属通信网的组成、威胁等级等提供重要的决策依据。运用电台个体识别技术，在复杂的战场电磁环境中监测敌方电台的活动的同时，能分析识别判断出敌方重要电台，进行有重点的侦收和电子干扰。同时，电台个体识别技术还可用于民用电磁频谱管理。因此，通信电台的细微特征提取分析和个体识别问题日益受到重视。

1 通信电台细微特征提取的研究现状

通信电台个体识别是通信对抗领域的难题之一。国外的研究始于20世纪末，国内的研究起步较晚。中电集团下属的几个研究所等多家单位已开始这方面的研究，研究重点从电台的暂态信号分析逐渐转移到电台稳态信号的分析，但相关研究公开资料较少。

相对于通信电台暂态信号特征分析提取，稳态信号的细微特征提取更为困难。因为在稳定工作状态下，通信信号源个体差异在信号上是合成的，很难对所有设备内部差异对信号的影响进行数学建模。通信电台发送端组成原理如图1所示。

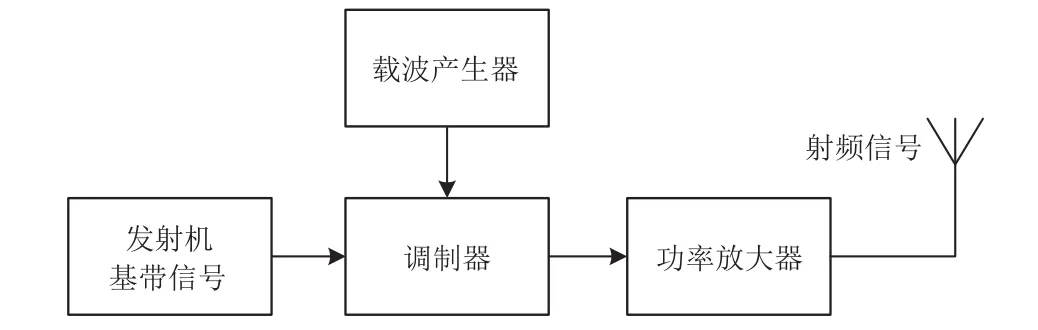
图1 通信电台信号发送端原理

（1）信号的载频偏差。同制式的两部通信电台虽然具有相同的标称频率，但基准频率和稳定度均有一定的容差。理论上，精确地测定电台个体之间的载频偏差，能作为细微特征识别电台。

（2）信号的调制参数。通信信号都是调制信号，其中调制参数的偏差是最容易考虑到的细微特征。但在非协作的情况下，电台调制识别和调制参数的估计给调制参数的偏差测量带来了困难。

（3）电台的杂散特征。电台的杂散效应主要来源于频率源和射频放大器。对于频率源，以DDS为例。杂散效应包括幅度量化误差、相位截断效应、参考时钟相位噪声和DAC非理想特性等。射频放大器的杂散效应则包括频率域的失真和时间域的失真。频率域的失真是由放大器振幅和相位特性的非线性造成的，而时间域的失真是由信号寄生相位或振幅调制造成的。

目前的研究热点主要是电台的稳态特征，尤其是电台的杂散特征提取技术[1]。射频放大器的非线性和内部噪声等产生的无意调制，以及频率源的不稳定性对信号频率的影响带来了电台杂散特征。由于信号细微特征具有非线性、非高斯性、非平稳的特点，利用高阶统计量的方法分析提取具有较大的优势。所以，目前研究包括各种形式的高阶谱特征[2-4]，特别是双谱特征[5-7]，作为通信电台的细微特征。但是，双谱特征需要二维模板匹配，造成计算复杂度高，所以针对双谱二维模板的降维处理提出积分双谱和选择双谱等方法。积分双谱如矩形积分双谱、圆周积分双谱等，虽然降低了二维模板的维数，但是会造成部分相位信息被丢失或重用，从而影响电台个体识别的准确性。选择双谱法采用Fisher测度筛选，对于类间分离度具有很多的准确度。将其作为电台个体的特征参数，能有效抑制交叉项对识别结果的影响，但选择双谱法对噪声的抑制能力较弱。

2 基于信噪比估计与分形维数的细微特征提取技术

本文主要研究通信电台的稳态特征，利用通信信号的分形特征包括盒维数、步维数及信息维数完成对信号稳态特征的分析提取[8]。由于分形特征需信号的包络进行分析提取，所以需利用希尔伯特变换提取信号的包络。信号包络与信号信噪比相关，在不同信噪比条件下分析提取的分形特征不同。尤其在信噪比较低时，分析特征有着明显的差异。所以，本文给出了信噪比-分形特征联合估计算法，在信号的信噪比估计的基础上，利用分形维数提取信号的细微特征。

2.1 信噪比估计

假设信道为加性高斯白噪声信道，接收信号的未调制模型如下：

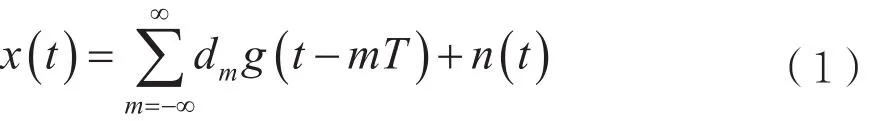
式中，E[||dm||2]=1，dm为发射符号序列；g(t)为传输函数；T为符号周期；n(t)为均值为0、方差为σn2的高斯白噪声。采样速率为fs=L/T，则式（1）可表示为：

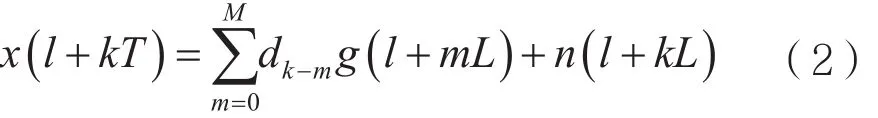
式中，l=0,1,…,L-1。

通过变换可得到信号功率、噪声功率和信噪比的估计值为：

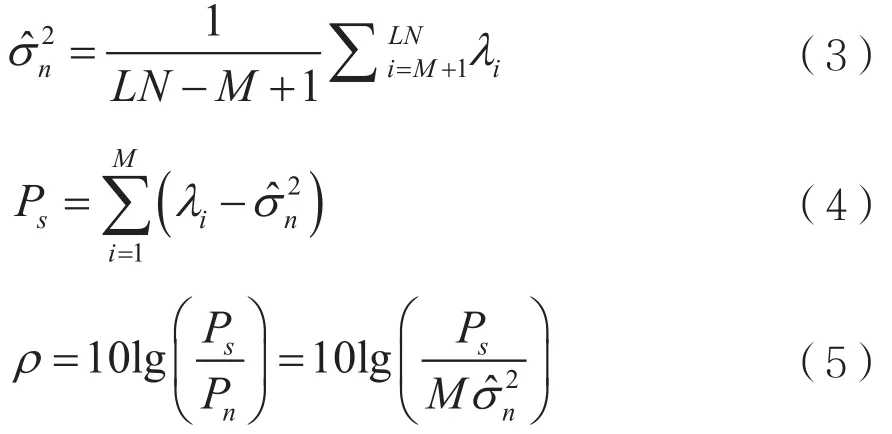
2.2 信号包络的分形维数

在信号信噪比估计的基础上，本文利用分形维数提取信号的细微特征。由于在同一信噪比时，信号的包络特征稳定，所以信号的细微特征基本相同，可建立通信电台信噪比-分形维数的特征库作为匹配模板，快速完成通信电台的个体识别。

分形理论是研究非平稳信号包络复杂度的有力工具，主要参数——分形维数可定量描述分形集的复杂性。其中，盒维数能分形集的几何尺度、步维数能反映分形集的粗视化程度；信息维数则能反映分形集的分布信息。

2.2.1 盒维数

分形理论中，盒维数可以定量描述信号包络变化的特性，反映分形集的几何尺度。设一度量空间为(X,d)，ε为非负实数，A是X中的一个非空子集，令N(A,ε)表示覆盖A的最小闭球的数目，闭球的半径为ε，即：

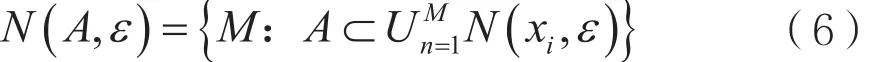
其中，x1,x2,…,xM是X的不同的点。设A是一个紧集，ε是非负实数，若存在：

则称Db是集合A的分形维数，记为Db=Db(A)，并称分形维数Db为盒维数。提取信号包络的盒维数实现如下：

（1）提取通信信号的包络s(i)，其中i=1,2,…N；

（2）令：

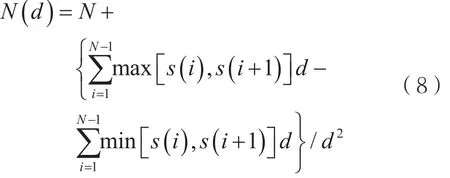
得到该信号包络的盒维数为：

2.2.2 步维数

步维数反映分形集的粗视化程度，利用相关函数来求分形维数。设在坐标X处，空间随机分布某量的密度为P(X)，则相关函数可定义为：

其中AVE{·}表示平均，r表示两点距离。当相关函数为幂型时，由于不存在特征长度，则分布为分形，此时有C(r)∝r-α。其中，α为幂指数，它与分形维数Db的关系为：

其中d是欧式空间维数。提取信号包络的盒维数实现如下：

（1）提取通信信号的包络s(i)，其中i=1,2,…N，并对其进行归一化：

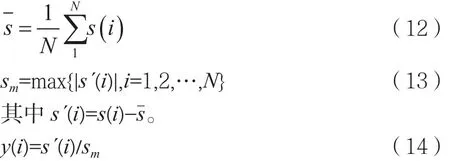
经过处理的y(i)是在[-1，1]区间的无量纲值。

（2）设步长为d，将横轴区间分成m段小区间，可波形的总长度为：

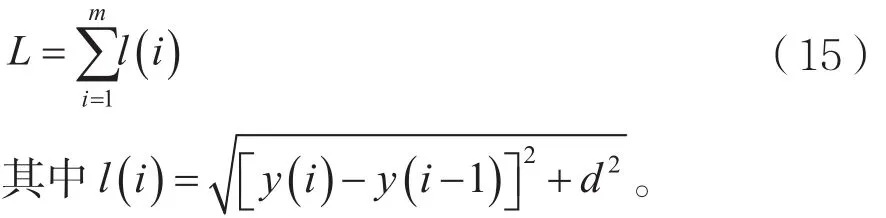
（3）根据步长d与步数N的关系，可得到波形总长度L为：

可通过不同步长d对应的总长度L估计α，得到步维数为：

2.2.3 信息维数

信息维数反映了分形集的分布情况。设X是Rn的集合，{A(i),i=1,2,…,N}是X的一个有限δ-覆盖，令Pi表示集合X的元素落在集合Ai的概率，其值为：

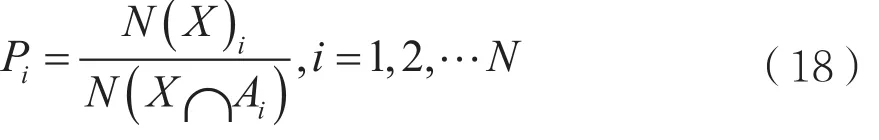
其中N(X)i与N(X∩Ai)分别表示元素的个数。令信息熵HI作为X的位形熵。

若信息熵满足关系HI～lgδDI，则X的信息维数定义为：

信号包络信息维数的计算方法如下：

（1）提取通信信号的包络s(i)，其中i=1,2,…,N；

（2）对信号包络序列进行重构：

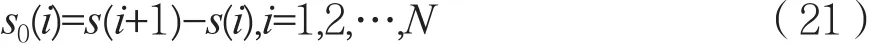
（3）计算信息维数。

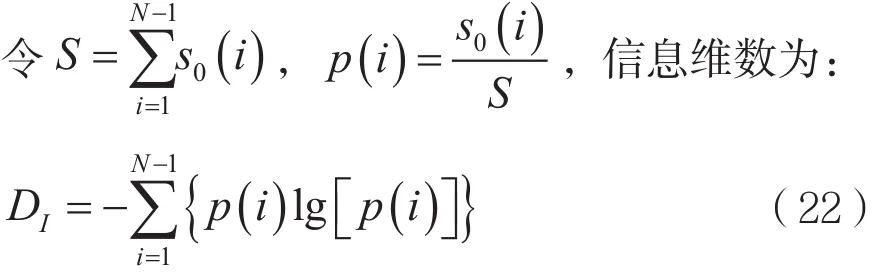
3 试验验证

3.1 细微特征提取验证

两部型号相同的短波电台，电台发射频率为28.88 MHz，调制方式为单边带调幅，采样频率为fs=2.38f。每部电台发射2组信号，分别计算每组信号的盒维数、步维数和信息维数等细微特征，如表1所示。

表1 同种型号电台不同个体之间细微特征差异

3.2 细微特征分类识别验证

采用最邻近分类法对两部电台进行识别，将每部电台数据1的提取特征作为电台的细微特征，数据2的提取特征为待识别的特征。每部电台采集实测数据1 000组，分别根据数据1的盒维数、步维数、信息维数计算正确识别个体电台的百分比，识别结果如表2所示。

表2 同种型号电台不同个体之间细微特征识别正确识别率

4 结 语

对通信电台个体而言，即使两部型号相同的电台也会存在细微差异。本文针对通信电台的稳态信号，在估计电台信号信噪比的基础上，利用分形理论分析提取信号包络的盒维数、步维数及信息维数，并将其作为通信电台的细微特征进行个体识别，取得了较好效果，为复杂电磁环境下的通信电台个体识别提供了新的思路。