一种基于堆栈自编码器的水声信道均衡算法*
刘振兴,陈 震
(1.泰州职业技术学院 信息技术学院,江苏 泰州 225300;2.南京信息工程大学 江苏省大气环境与装备技术协同创新中心,江苏 南京 210044)
0 引 言
近年来,水下无线通信在各种领域得到了广泛应用。人们越来越关注水声通信系统的研究,提出了常数模、小波和多小波等多种水声信道均衡算法[1-3]。其中,常数模算法(Constant Modulus Algorithm,CMA)因结构简单、性能稳健、运算量小而被广泛使用,但其收敛精度不高。小波和多小波算法的均衡效果与其变换的稀疏能力有关,且需事先选取小波和多小波系数,影响了算法的实际应用。均衡器完成的是一个非线性映射,可以描述为观测空间的决策区域划分问题,而神经网络可以形成比较复杂的非线性决策曲面,因此可以利用神经网络设计均衡器。文献[4]设计了基于BP神经网络的均衡器,对语音信号均衡算法进行了研究。文献[5]将RBF神经网络作为均衡器,对水声信道低阶调制信号的均衡进行了研究。文献[6]将非单点模糊化技术引入RBF网络,设计了非单点模糊径向基函数(Radial Basis Function,RBF)网络判决反馈均衡器,对均衡器的抗突发干扰能力和误码性能进行了研究。常规的神经网络一般是多输入单输出系统,数据的处理能力有限。深度学习技术的出现,为处理这类问题提供了一个很好的方向。该技术不强调数据的先验特性,通过端到端的设计搭建网络模型,注重模型的简单和通用,具有处理能力强、泛化性能好等特点。其中,降噪自编码器可以模拟人脑思维方式,提取低噪数据特征,重构无噪数据,且网络结构简单、算法复杂度低,广泛应用于机器视觉、图像处理等领域[7-8]。但是,网络的性能与其结构有关,要想获得较好的性能,浅层网络所需节点数与输入数据数目呈指数关系,而深度网络在间接性和表达能力上更具优势,所需节点数与输入数据数目呈多项式关系,特别是与自编码网络对应的堆栈自编码网络可以模拟人的大脑活动,逐层提取输入数据特征,表现更优。文献[9]对堆栈去噪自编码器的构建策略进行了研究,采用“贪婪法”逐层训练整个深度网络。实验结果表明,随着隐层层数的增加,网络性能不断进化,且预训练后的网络性能优于无预训练的网络。但是,均衡与去噪不同。均衡实现的是逆向滤波过程,目的是恢复发射信号。深度去噪自编码网络的训练方法不适于均衡器,而神经网络处理的是实数信号,通信中常见的高阶调制信号无法直接送入神经网络进行处理。
基于以上分析,本文对基于堆栈自编码器的水声信道均衡算法进行研究。该算法首先将自编码器作为均衡器,针对高阶QAM信号,采用信号变换降低信号的复杂度,通过多输入多输出变换,将串行的通信信号转换为并行信号输入均衡器进行处理,通过对比输出信号的误差值调整网络参数,直至网络稳定。在此基础上,进一步研究了基于堆栈自编码器的水声信道均衡算法。该算法将堆栈自编码器作为均衡器,采用“类贪婪法”逐层训练自编码均衡器,然后反向微调整个网络。水声信道仿真结果表明,基于自编码器的均衡算法和基于堆栈自编码器的均衡算法都具有较好的均衡性能,其中堆栈自编码器算法表现更优。
1 基于堆栈自编码器的水声信道均衡算法
1.1 自编码器
自编码器是一种自监督网络,理想状态下其输出等于输入。通过建立合理的损失项,可以实现无监督学习下隐层特征的提取。特别当输入特征彼此相关时,自编码学习算法可以提取输入数据中的相关性。进一步,以其提取的特征作为新的输入,通过参数学习可以获取对应的编码特征。三层自编码器网络结构如图1所示。
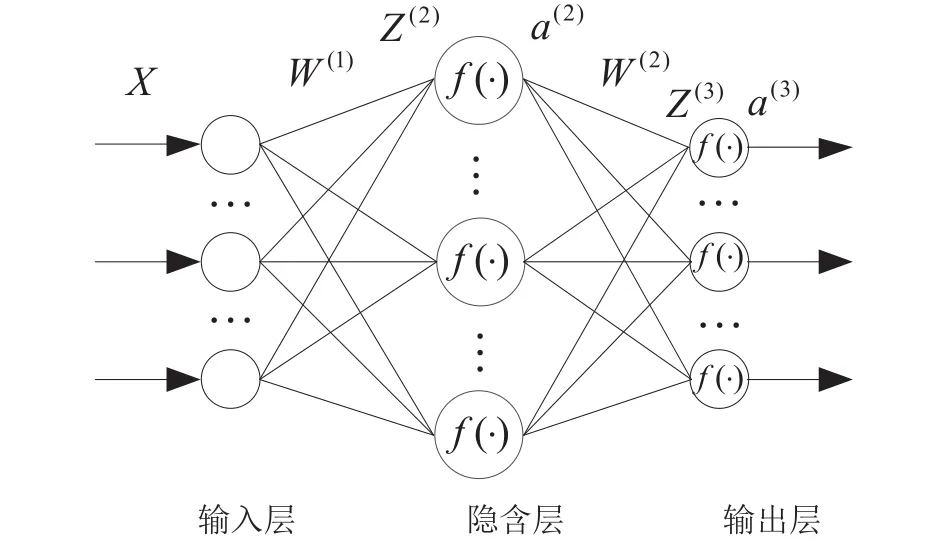
网络计算公式如下:

其中,X∈Rn表示输入数据,W(L)表示网络第L+1和L层之间的连接权值,Z(L)表示第L层的输入,a(L)表示第L层输出,b(L)表示与L+1层节点相连接的偏置,f(·)表示激活函数。
假设训练集合包含m个训练样本{(X(1),Y^(1)),…,(X(m),Y^(m))},采用批量梯度下降法对网络进行学习,单样本的代价函数定义为:
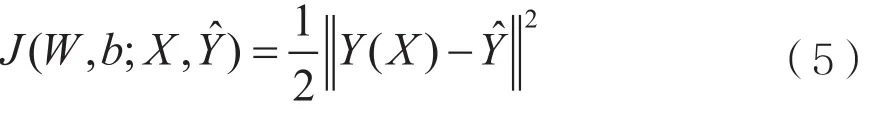
总样本代价函数定义为:
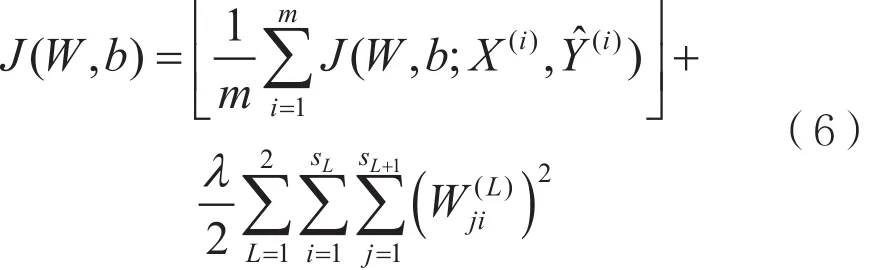
式中,第一项为均方误差项,第二项是正则项,目的是减小权重的幅度,防止过度拟合。λ为权重衰减参数,用于控制公式中两项的重要性;sL表示第L层的神经元个数。
1.2 堆栈自编码器
堆栈自编码器即将多个自编码器堆栈而成,具有3个隐含层的堆栈自编码器网络结构如图2所示。

图2 堆栈自编码器网络结构
网络计算公式如下:

堆栈自编码器通常采用逐层贪婪法进行训练[9]。本文对此进行了改进,采用“类贪婪法”逐层训练自编码均衡器,训练过程如下。
(1)用带标签的训练样本{(X(1),Y^(1)),…,(X(m),Y^(m))}训练第一个自编码均衡器,得到参数W(1,1)、W(1,2)、b(1,1)、b(1,2),其中X为均衡器输入信号,Y^为对应的均衡器期望输出。
(2)利用W(1,1)和b(1,1)得到输入X和Y^的一阶特征表示 h(1)(k)和 h(1)´(k),将 h(1)(k)和 h(1)´(k)分别作为第二个自编码均衡器的输入和期望输出进行训练,得到参数 W(2,1)、W(2,2)、b(2,1)、b(2,2)。
(3)依次类推,直至训练完整个网络。注意在训练某层自编码器时,保持其他层自编码器参数不变。
1.3 信号变换
当信道传输高阶信号时,考虑到网络特性,为了降低信号处理的复杂度,需要在均衡器的输入端做信号变换,将复数信号变换为实数信号。为了使信号不失真,在均衡器的输出端需做信号反变换,将实数信号变换为复数信号。
当发射信号为16QAM信号时,星座图如图3所示。
图3 发射信号
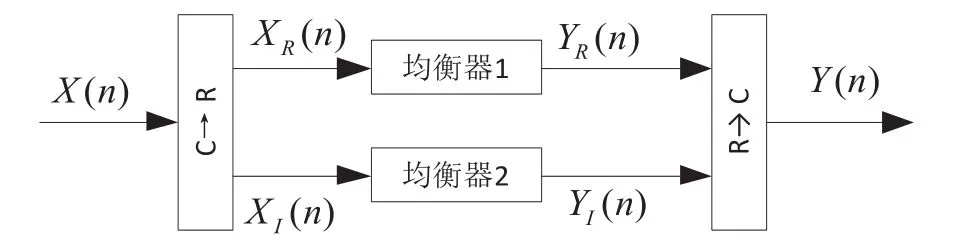
图4 信号变换原理
图 4中,X(n)=[x(n),x(n-1),…,x(n-L+1)]为均衡器输入的复数信号,其中L表示均衡器的长度,X(n)=XR(n)+jXI(n)。对X(n)进行信号变换转换为两路实数信号XR(n)和XI(n),分别送到均衡器进行处理。YR(n)和YI(n)为与之对应的两路均衡器输出信号,经过信号反变换后转换为复数数信号Y(n),Y(n)=YR(n)+jYI(n)。变换原理为:

1.4 算法描述
本文提出了基于堆栈自编码器的信道均衡算法。该算法将堆栈自编码器作为均衡器,当发射高阶信号时,先将均衡器输入信号进行复实变换转换为两路实数信号,然后分别经串并转换送入均衡器进行处理,再在均衡器的输出端作并串转换和实复变换。算法原理如图5所示。
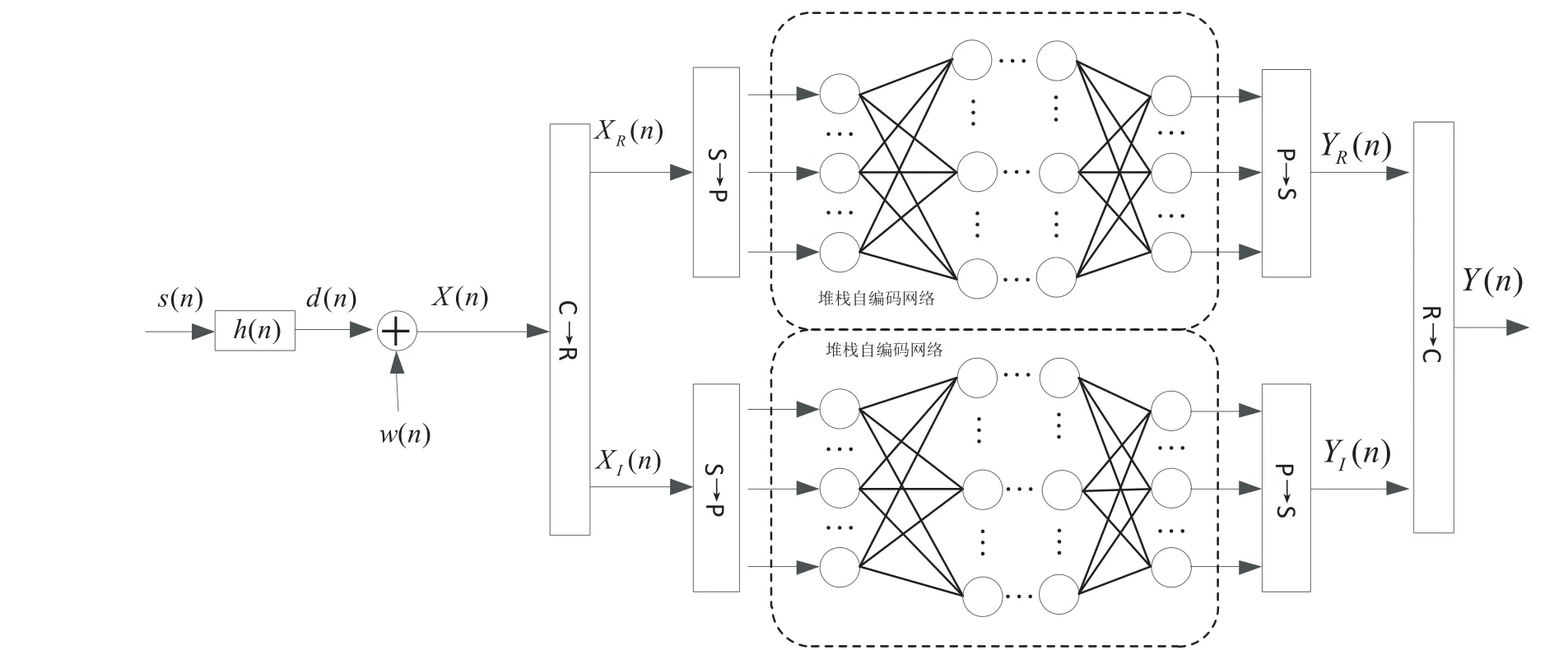
图5 基于堆栈自编码器的信道均衡算法原理
图5 中s(n)为发送的复数信号,h(n)为传输信道,d(n)为信道的输出信号,w(n)为加性高斯白噪声,x(n)为均衡器输入信号,Y(n)为均衡器输出信号。
均衡器输入为:
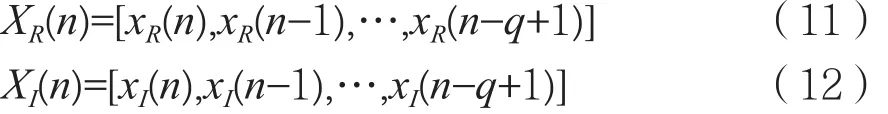
式中,q为堆栈稀疏自编码网络输入层神经元个数。

式中,p为水声信道h(n)的长度。
堆栈自编码器的训练分为两部分:
早在20世纪40年代,Queney(1948)、Scorer(1949)和Scorer and Klieforth(1959)就从线性化的大气运动方程组出发,分别建立了二维条件下单层和二层的大气背风波的理论模型及其存在条件。Lyra(1943)从流体力学角度在一定的假设条件下试图找到过山气流的解析解。叶笃正(1956)在50年代对背风波理论进行了系统的总结。巢纪平等(1964)以两层密度不同的流体模式为基础,讨论小地形对气流的影响,研究了背风面“气压跳跃”的形成过程。这些都是对背风波比较早期的研究,但其影响却是极其深远的。
(1)如前面所述,采用“类贪婪法”逐层训练自编码均衡器。考虑到信号的特性,文中激活函数选择tanh函数,即f(z)=(ez-e-z)/(ez+e-z)。
(2)微调
①根据式(7)和式(8)进行前馈计算,计算各层的激励响应。
②计算残差。
输出层:

隐含层:
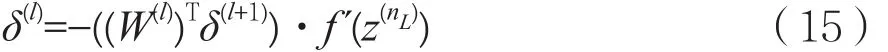
其中l=2,…,nL-1。
③计算单偏导数。
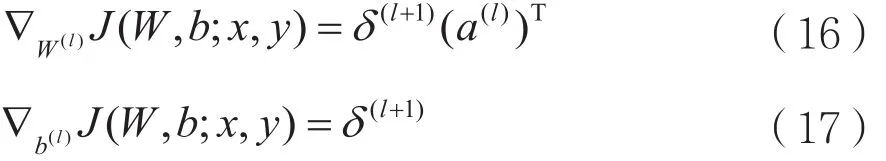
④计算总样本偏导数。
对样本i=1到m,计算:
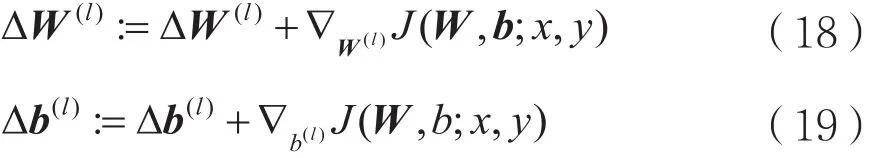
其中ΔW(l)为与W(l)相同大小的矩阵,Δb(l)为与b(l)相同大小的向量,初始值为0。
⑤更新参数。
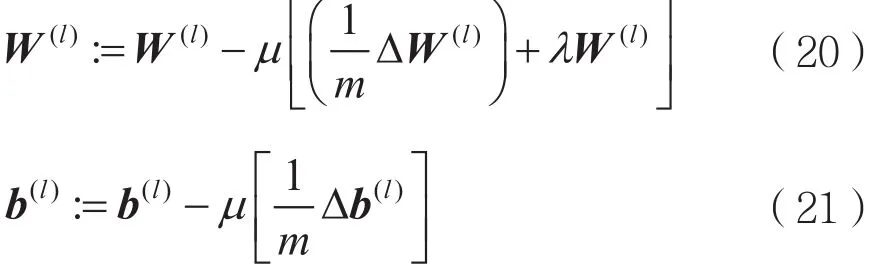
其中μ为学习速率。
基于堆栈自编码器的水声信道均衡算法主要步骤归结如下。
步骤1:根据式(9)和式(10)采用信号变换方法,将均衡器输入的复数信号变换为实数信号,并经过串并转换后送入堆栈自编码网络进行处理。
步骤2:采用“类贪婪法”逐层训练自编码均衡器。
步骤3:根据式(7)、式(8)和式(14)~式(21)微调堆栈自编码均衡器,直至网络稳定。
步骤4:计算网络稳定后的输出值。
步骤5:通过并串转换和实复转换将实数信号恢复为复数信号。
2 计算机仿真与性能分析
为了比较CMA、REA、AEA和SAEA共4种算法的性能,采用典型的混合相位水声信道进行仿真实验,对比其在不同信噪比下的均方误差值以及20 dB输入信噪比下的均衡器星座图。实验中发射信号为16-QAM,序列长度为12 000,AEA算法中采用自编码器作为均衡器,SAEA算法中采用堆栈自编码网络作为均衡器,相关实验参数如表1所示。
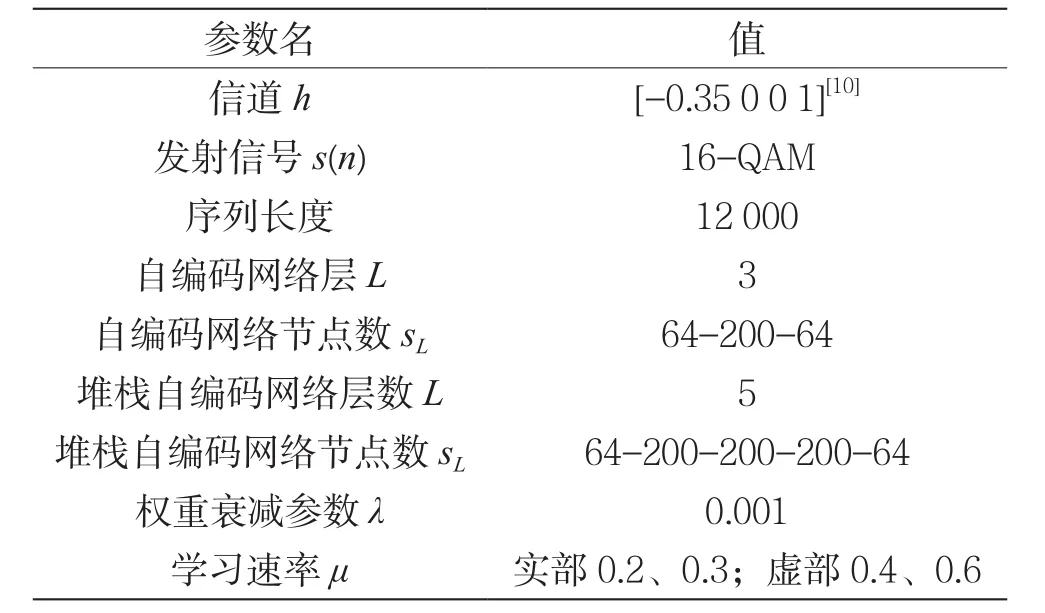
表1 实验参数设置
表2为不同输入信噪比下4种算法的均方误差。由表2可知,AEA和SAEA的均方误差小于CMA和REA均方误差。当输入信噪比较大时(15~25 dB),AEA的均方误差比CMA小4.5 dB左右,比REA小1.4 dB左右,SAEA的均方误差比AEA小0.4~1.5 dB;当输入信噪比较小时(5~10 dB),AEA的均方误差比CMA小1 dB左右,比REA小0.4 dB左右,而SAEA的均方误差显著减小,说明输入信噪比较小时,SAEA的均衡效果更突出。
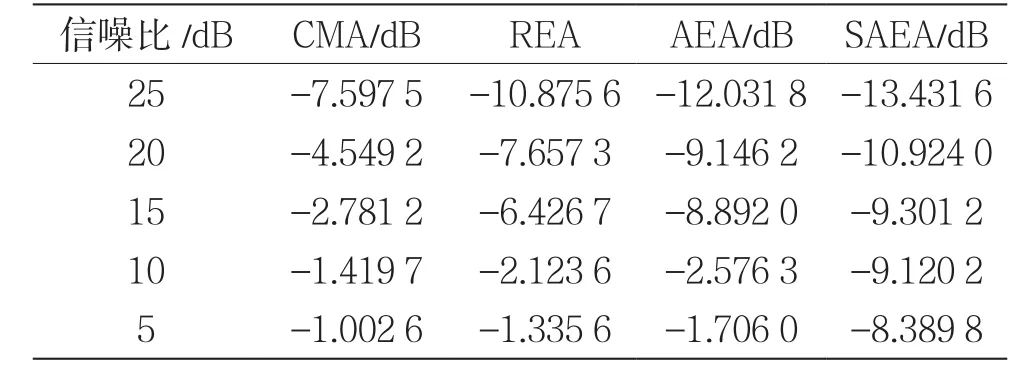
表2 不同信噪比下的均方误差
图6为20 dB输入信噪比下均衡器星座图。由图6可知,4种算法都能恢复发射信号,但CMA的星座图较松散,而REA、AEA和SAEA的星座图较紧凑,特别图6(e)所显示的星座图最集中、最清晰,说明SAEA算法的均衡性能最优,抗干扰能力最强,其次为AEA算法。

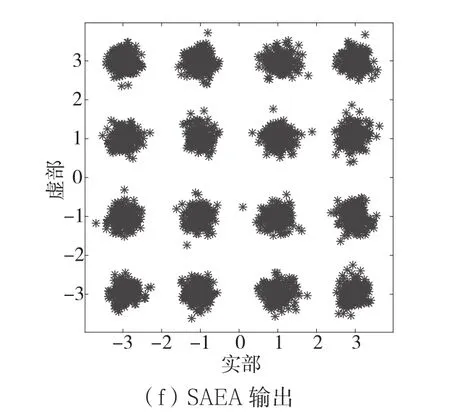
图6 星座图
3 结 语
自编码器在信道均衡中的应用类似于其在图像去噪和图像超分辨率的应用,通过对样本的学习构建网络模型,建立输入数据与期望输出之间的对应关系。本文采用堆栈自编码器作为均衡器,并提出了一种“类贪婪”法逐层训练自编码均衡器。与其他信道均衡算法相比,本文提出的算法具有更好的均衡性能和鲁棒性,且不需要知道具体的信道模型,系统可以直接从数据中学习网络参数。当使用的环境改变时,网络结构可以保持不变,只需要重新训练网络,更新参数。

