基于多阶误差曲面的纹理合成

(河南理工大学 计算机科学与技术学院，河南 焦作 454150)

纹理合成[1]是在给定小样图的纹理特征基础上，利用其已有的纹理结构特征合成一个大面积纹理图像，并保证纹理结构的相似性与连续性。纹理合成是为了避免纹理映射中产生裂缝走样亦或存在接缝等现象而提出的，将人工合成纹理图像作为目标，在样本图像中搜寻匹配点，将其复制到输出图像中来生成与样本相似的连续纹理，是计算机图形图像处理领域中的重要研究内容。纹理传输是在纹理合成的基础上发展起来的，然而它又和纹理合成技术不同，纹理合成仅需一小块样本图像就能够合成任意大小的纹理图像，而纹理传输则涉及到两个图像，把源图像的纹理特征传递到目标图像上，从而形成具有源图像纹理风格的艺术图像，纹理传输这一特性使其在许多方面都有应用价值。

Efros[2]提出的基于块拼贴的纹理合成(Image Quilting)算法，通过寻找最小误差路径来实现块之间的拼接，得到了良好的结果，使图像拼接过程过于随机导致的结构性纹理合成结果不理想的问题得到了解决；Schlömer[3]等人对Wang Tiles方法进行扩展，用于半随机纹理的合成；Zu[4]等人使用Wang Tiles方法实现了纹理合成；孙劲光、王继东[5-6]等人提出了基于Wang Tiles的改进纹理合成算法，提高了纹理合成算法结果的质量；沈哲[7]等人运用并行方式提高了纹理合成算法的效率；Wei[8]等人提出一种基于搜索的纹理合成算法，其中样本可以按任意顺序生成，但结果纹理保持相同；Wu[9]等人提出一种特征感知方法来合成自然纹理。

Image Quilting算法相比基于像素的合成算法在时间和效果上得到了改善，但仍存在缺点：合成的纹理结果会出现重复现象，如果样图较小时将会更明显；对许多结构性比较强的纹理和一些自然随机纹理如草丛、水波会造成边界不连续，合成的结果不太理想，Raad，Kuri及Lasram[10-13]等人提出了相关的改进算法。本文对Image Quilting算法进行改进，通过多阶误差曲面来计算最小误差分割路径，使得到的拼贴路径更加精确，达到更好的合成效果。同时在按照路径拼贴纹理块后引入Poisson Blending来对边界不连续区域进行平滑处理，并且将其应用到纹理传输中。

1 Image Quilting算法

Image Quilting算法的基本思想是：按照扫描线的顺序，采用一定的匹配准则，从输入纹理挑选一定大小的纹理块复制到输出纹理，直到符合输出纹理图像的尺寸要求。如图1所示，图1(a)为样本纹理，图像中的红色方块代表纹理块；图1(b)为在样图中随机选取纹理块置于合成图中；图1(c)为在合成图中把纹理块置于重叠区域；图1(d)为在纹理块之间的重叠区域找到最小边界切割作为新纹理块的边界，并按切割路径缝合纹理块边界。

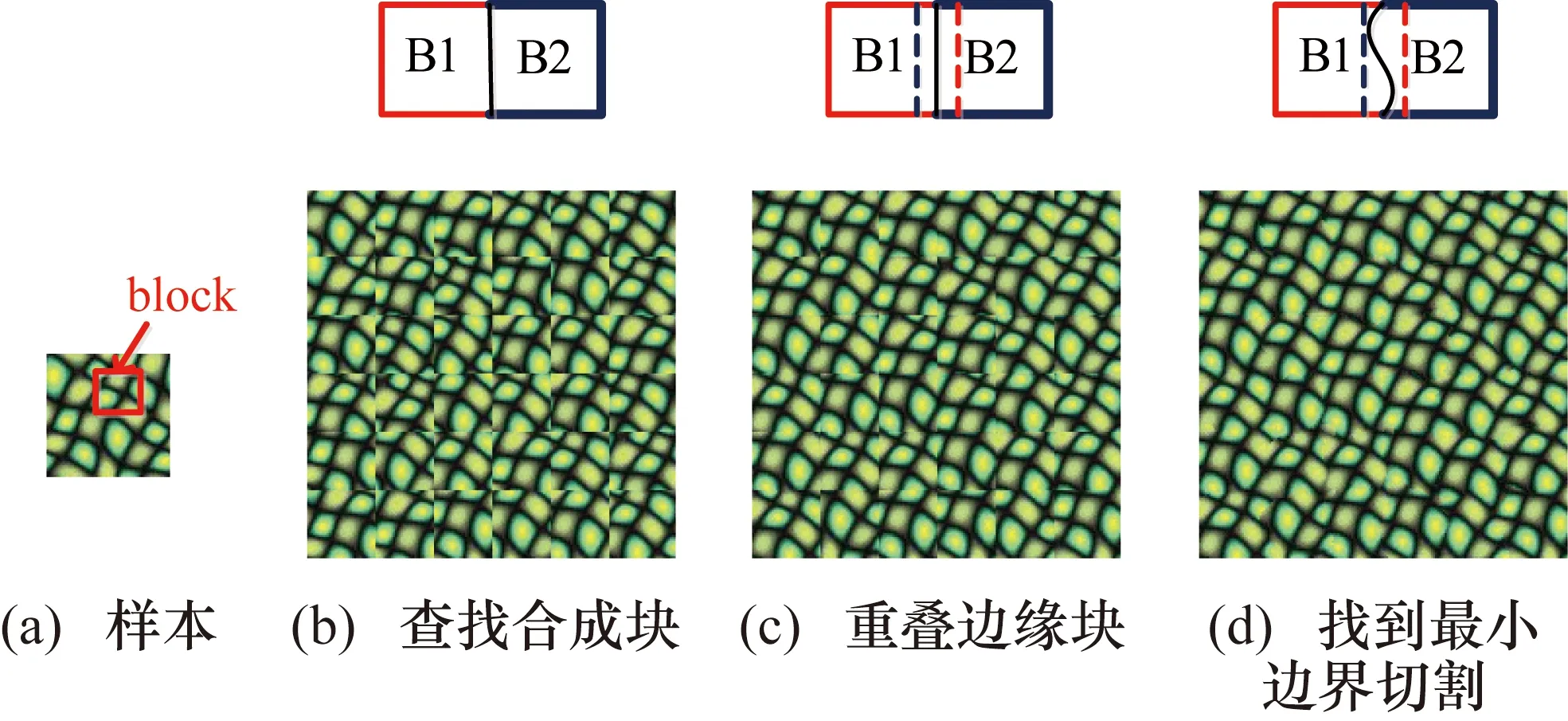
图1 重叠块间拼贴

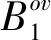
(1)

通过式(2)得到重叠区域最后一行的各点误差：

Ei,j=ei,j+min(Ei-1,j,Ei,j-1,Ei+1,j-1)

(2)

对于垂直方向的接缝，先在水平方向上逐行搜寻误差最小的点，通过误差曲面的最小垂直路径的终点即为E中最后一行的最小值，并且它回溯地从点集中找到一条路径最短的连线，所要寻找的最小误差边界切割就是这条连线。而水平的重叠区域可以采用类似的处理方式。既有垂直而且又有水平的重叠区域，最小路径则将在中间交汇，最佳切割路径被认为是重叠部分中所有最小值的连线。这样所得到的误差才能够最小，拼贴后的边界区域在视觉上也将更加光滑。

2 本文算法

2.1 多阶误差曲面

多阶误差曲面是在给出的像素值之间用N阶误差来定义误差曲面，将重叠区域的误差曲面定义为

(3)

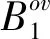
图2为N取不同值(2，4，8，16)时由样本图像所得到的合成结果，其中，图2(a)为样本图。可以看到当N取2时(图2(b))合成结果中明显有一些地方产生错误拼接，导致在边界处产生了不连续的现象，但是随着N值的增长，得到的合成结果中边界不连续现象得到明显改善。

图3为图2中各合成结果对应的误差曲面变化分析图，表1为N取2，4，8，16不同值时误差曲面值超过3000的个数统计、标准差以及计算时间表。可以看到，图3(a)为N=2的误差曲面图，经统计误差值超过3000的有47个；图3(b)为N=4的误差曲面图，误差值超过3000的有28个；图3(c)为N=8的误差曲面图，误差值超过3000的有22个；图3(d)为N=16的误差曲面图，误差值超过3000的有11个。通过分析图中误差曲面值可以得出：随着N的增长，误差曲面的值不断减小，误差曲面值越小，在两块之间的重叠区域得到的边界分割越精确。由误差曲面值的标准差(Standard Deviation，SD)比较可知，随着N值的增长，误差值的SD值越来越小，说明误差值的离散程度越来越小，同时计算时间上差别不大。

图2 不同N值的合成结果

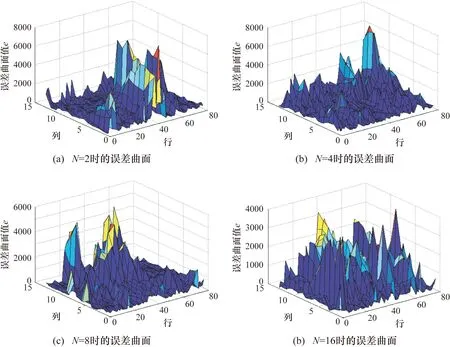
图3 误差曲面变化分析

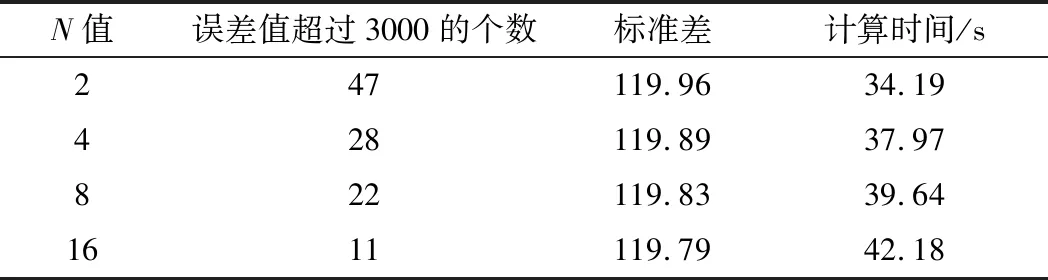
表1 N值变化时的误差值个数、标准差与计算时间

2.2 Poisson Blending

由于Image Quilting算法在拼贴块时容易产生接缝不连续的现象，这里在按照最小误差边界分割路径完成块拼贴之后，通过引入Poisson Blending来优化处理不连续区域，使其得到修复，令合成效果更好。Poisson Blending[14]是梯度域图像处理方法的一种，利用构造泊松方程求解像素最优值的方法，在保留源图像梯度信息的同时，可以很好地融合源图像与目标图像的背景。该方法根据边界条件求解泊松方程，实现了梯度域上的连续，从而达到边界处的无缝融合，这可以应用到图像修复中[15]。

引入Poisson Blending来对拼贴块接缝处进行平滑处理的原理如图4所示。

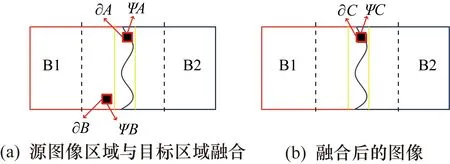
图4 Poisson Blending平滑处理

图4中，B1和B2是有重叠区域的两个纹理块，图中重叠区域切割路径(如图中曲线所示)左边为保留B1的部分像素，重叠区域切割路径右边为贴入B2的部分像素。在切割路径周围选取一定宽度的区域作为目标区域，即图中两条实线之间的区域,那么重叠区域所属B1部分除选作目标区域外的剩余区域则为源图像。如图4(a)中ΨB为将要与目标块ΨA融合的选中源图像块，∂A、∂B和∂C分别是ΨA、ΨB和ΨC的边界，如图中所示边界。该算法在尽可能多地保留ΨB梯度信息的同时调整ΨB的颜色信息，以便于即将形成的新图像块ΨC(如图4(b)所示)与图像剩余部分能很好地融合。

算法过程如下：

首先为了保证边界的等照度线可以适当地保持，令ΨC的边界像素值初始化等于ΨA的边界像素值，即

ΨC(x,y)=ΨA(x,y) ∀(x,y)∈∂B

(4)

接着限制ΨC的图像梯度与ΨB的图像梯度相同，与此同时ΨC中其余像素的RGB值(RGB代表红、绿、蓝3个通道的颜色)独立地调整为与边界像素值一致：

▽C(x,y)=▽B(x,y)∀(x,y)∈ΨC∂C

(5)

▽(x,y)表示像素(x,y)处的图像梯度。公式(5)求解时用含有i变量的线性方程通过迭代矩阵方法求解(i是ΨC(x,y)中的像素数量)，这里用Jacobi方法求解。引入Poisson Blending后得到的合成结果如图5所示。

图5 Image Quilting合成结果和引入Poisson Blending

图5(a)为原算法的合成结果，图5(c)为引入poisoon Blending的合成结果，图5(b)和5(d)分别为合成结果图中产生不连续的同一区域在改进前后的对比。

3 实验结果与分析

3.1 纹理合成

采用改进算法分别对自然纹理以及结构性纹理图像进行多组合成实验，如表2所示。将本文算法合成结果与Image Quilting算法合成结果进行比较，所有样例从左到右依次为输入样本n(n=1,2,3,4,5)、Image Quilting算法合成结果、文献[10]算法合成结果以及本文算法分别取N=4和N=8时的合成结果。本文所有实验结果都是通过Matlab程序，在2.50 GHz主频、2 GB内存的计算机上完成。

从表2中对样本1的算法合成结果可以看出：Image Quilting算法在对几行摆放的苹果进行合成时，苹果下方的隔开物品有几行产生了明显的断开，没有连续在一起，合成结果不理想；文献[10]中优化后算法的合成结果，也产生了同样的不连续现象；取N=4和N=8时的算法合成结果，可以看到不连续现象得到改善，合成结果质量提高。

对样本2的合成结果可以看到：Image Quilting算法与文献[10]算法对竹席进行合成过程中同样出现了拼接错误产生模糊和不连续的现象；而本文算法取N=4和N=8时能得到更好的合成结果。

对样本3的合成结果可以看到：Image Quilting算法和文献[10]算法合成结果中有纹理重复等边界不匹配现象，得到的结果不够自然；本文算法对样本3的合成结果避免了上述现象产生。

通过大量的实验结果可得，改进算法对结构性和自然纹理都能得到更高质量的合成结果。

3.2 纹理传输

表3为将上文中改进的纹理合成技术应用到纹理传输的结果，从左到右依次为源图像n(n=1,2)、目标图像和经过纹理传输之后的输出图像。第1行是将面包纹理作为源图像，将黑白人物照片作为目标图像，经纹理传输得到一个用面包纹理渲染出来的人物图像，该图像和目标图像人物照片是相似的，然而照片人物的纹理却变成了面包。第2行是将米饭纹理作为源样本纹理，将人物图像作为目标图像，应用纹理传输后得到一个以米饭颗粒为纹理的人物图像特效。从图中可以看出传输结果在保持源图像和目标图像的图像特征的基础上得到了比较好的效果。

4 结束语

提出了一种基于多阶误差曲面的纹理合成改进算法，通过改变误差曲面公式的阶数来得到更精确的最佳切割路径，使得拼接时结构信息保持得更好；并且在找到最佳切割路径完成纹理块的拼贴后引入Poisson Blending对纹理合成中出现接缝不连续的现象进行了优化，将这种改进的纹理合成技术应用到纹理传输中。通过实验验证了本文算法对纹理合成的结果有所改善，能够适用于结构和自然随机纹理。今后会在算法的计算性能方面做进一步的优化改进，以提高算法的效率。

表2 本文算法合成结果与Image Quilting算法及文献[10]算法合成结果对比

表3 纹理传输结果