试卷讲评课如何培养核心素养

李德俊　王建民

【摘要】本文首先介绍了试卷讲评课的现状与问题、相关概念，然后以2018年北京市朝阳区高三数学理科二模试卷的第18题为例从三个方面重点论述了在试卷讲评课中如何培养数学核心素养，主要从不同的解法，不同的设问，不同的思维方式和引导方式来提高试卷讲评课的效率，来培养和发展学生的数学核心素养.

【关键词】试卷讲评;直观想象;数学运算;逻辑推理;核心素养;零点

【基金项目】北京市教育科学“十三五”规划2017年度一般课题：依托工作室提升数学教师数学教育理论素养的研究（CDFB17343）研究成果之一.

《普通高中数学课程标准（2017版）》指出：“数学教学活动的评价的目的是考查学生学习的成效，进而也考查教师教学的成效.通过考查，诊断学生学习过程的优势与不足，进而诊断教学过程中的优势与不足;通过诊断，改进学生的学习行为，进而改进教师的教学行为，促进学生数学学科素养的达成.”为了实现上述评价目的，教师应坚持以学生发展为本，以积极的态度促进学生不断发展，应重视学生数学学科素养的达成[1].

一、试卷讲评课的现状分析与问题

从形式上常见的几种讲评类型主要有：灌输式讲评、匆忙型讲评、流水型讲评和校正型讲评.灌输式讲评即教师在讲评试卷时，自顾自依照题目讲解分析，给出答案，学生忙着修改;匆忙型讲评即没有对学生的得分情况，典型错误进行认真的总结，在试卷讲评时不能做到有的放矢，缺乏针对性和条理性.

由上述现状分析可以看出，试卷讲评课的问题主要有部分教师对待试卷讲评课的重视程度不够，设计不充分，形式单一，缺乏新意，思维没有深度.

二、试卷讲评课的相关概念梳理

目前我国学者对试卷讲评课概念的界定尚未形成统一的定义.王晓娟在《高三试卷讲评课高效教学策略》中把試卷讲评课概括为：在考试过后师生共同对试卷结构、考情进行分析，纠错并进行错因分析与归类，以查缺补漏，从而使学生巩固所学知识，最终提高解决问题能力的一种课型.蒋金珍在《高三试卷讲评课的问题与对策》中提到，试卷讲评课是指学生在考试结束后，教师对试卷进行解剖、分析、点评，以达到帮助学生完善知识结构、提高审题和解题能力、掌握学习规律的教学活动[2].

三、试卷讲评课的教学环节设计

基于上述学习和分析，在高三的试卷讲评课的教学中，笔者大胆地进行尝试，完善了试卷讲课的模式，更注重培养学生的数学核心素养，下面以2018年北京市朝阳区高三数学理科二模的18题为例谈一下自己的做法.

题目 已知函数f（x）=xex+ax2+2ax（a∈R）.

（Ⅱ）当-12≤a<0时，讨论函数f（x）的零点个数.

（一）作答展示，落实基础

从设计上要打破灌输式讲评，课上为了节省时间，讲评更有针对性，在课前对学生的答题情况及解题中遇到的困难进行交流并做详细的统计，此题第二问9分，班级平均分5分，班级共有43名学生，其中有30名学生采用直接对函数f（x）分类讨论，主要存在的问题有：讨论得不够全面，没有注意细节，分类不清，没有画图意识.因为此题是借助导函数图像得出原函数图像，再由极值的正负决定零点的个数，部分学生没有关注函数图像，会感到不知所措，那么在讲评前笔者让学生先自己独立地进行改正，让做错的学生代表展示二次作答情况，借此规范解题步骤，解决学生的难点，然后教师引导学生总结应用这种解法解题的突破口即利用导数研究函数的单调性，数形结合必不可少.这样通过对解题的常规方法进行再回顾，再反思的过程，能够用严谨的数学语言表达数学结论，来发展学生的逻辑推理、数学运算、直观想象三大核心素养.

（二）解法优化，培养能力

上述解题思路分类讨论比较复杂，要求学生具备较强的运算能力，为了减少运算的复杂性，让有分类讨论想法的学生在原有基础上有新的突破，所以引导学生从研究问题的本质出发，即从零点的定义出发，根据方程f（x）=0可以得出一个零点为f（x）=0可以得出一个零点为x=0，即改变原函数的结构特征f（x）=x（ex+ax+2a），于是求函数f（x）的零点的个数转化为求函数g（x）=ex+ax+2a的零点个数，学生很快发现函数g（x）与前面函数f（x）相比较，减少了讨论的情况，使复杂问题简单化，大大降低了运算量，增强解题的信心.这种设计既关注了四基四能，又让学生在原有的基础上尽量化繁为简，这样坚持下去，学生的直观想象、数学运算的核心素养从一级水平上升到二级水平，过程中提升推理论证能力，培养了逻辑推理的核心素养.

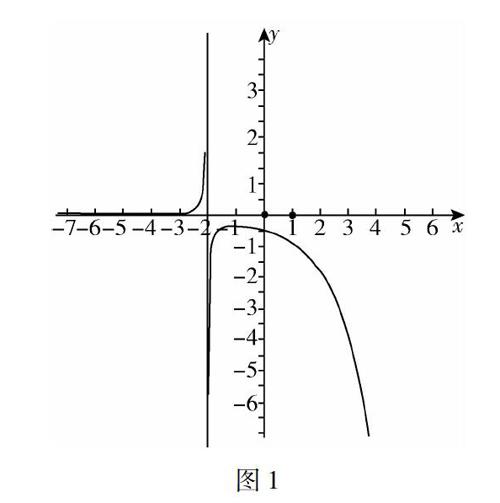
学生：欲求函数f（x）的零点的个数，等价于求方程f（x）=0的根的个数，此题可以采用分离参数的方法解决，过程中发现x=0是f（x）的一个零点，x=-2不是函数f（x）的零点，所以改变方程ex+ax+2a=0的结构，变成a=-ex（x+2）（x≠0，且x≠-2），转化为函数y=a与函数y=-ex（x+2）（x≠0，且x≠-2）图像交点的个数.给出时间让学生研究，然后让学生板演，展示作答情况.函数y=-ex（x+2）（x≠0，且x≠-2）图像，如图1所示.

图1

每种解题方法结束，教师要引导学生分析这种解法的优劣即解后总结反思，学生畅谈感想，虽然研究的函数不含参数，但解决新函数时，产生了一条渐近线，学生容易忽略，推理论证困难，这些对学生容易产生障碍.因此，用导数研究函数图像是有局限性的，所以借助于极限和函数值的正负来辅助表达，这个环节的设计不仅关注了学生的思维障碍，而且关注了学生的解题习惯、总结反思的习惯.

（三）方法总结，形成规律

试卷讲评课主要以试题分析为主，除了知识上的分析，对解题规律的总结也是不可缺少的环节，但这个规律最好是在讲评过程中逐渐渗透的，让学生在分析每种解法的过程中潜移默化产生的，所以还是让学生自己总结出求函数零点或零点的个数的一般方法，如图2所示.

在高中的试卷讲评课的设计中，不仅能让学生被数学问题吸引，并能通过对这些问题的思考达到提高数学思维的目的，不是讲讲几道题的解法就可以实现的，而是需要我们在课堂教学的各个方面去不断地探索与实践[3]，从而形成和发展数学学科核心素养.

【参考文献】

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018：84.

[2]李典.数学试卷讲评课的现状调查与分析[D].北京：首都师范大学，2014：15-18.

[3]张鹤.数学教学的逻辑——基于教学本质的分析[M].北京：首都师范大学出版社，2016：130-131.