直觉体悟：获得概念的新路径

张晓霞

摘要：数学概念是人类思维创造的抽象实体。直觉主义哲学特别强调人的直觉对数学概念的作用，认为“纯粹直观”是数学概念产生的基本依据。以“公倍数和最小公倍数”的教学为例，让学生在纯粹感知过程中实现对公倍数和最小公倍数概念的构造，精准回归倍数和因数作为“数”的身份特质，抓住它们表征数与数之间的“关系”实施教学，是促使小学生理解、掌握和运用数学概念的关键。

关键词：直觉体悟;数学概念;小学数学教学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2019）10B-0029-04

一、研究缘起

直觉主义哲学认为数学必须依靠原始直觉，只有在“纯粹直观”里，人类才能先天、具体地把一切概念构造出来。[1]苏教版小学数学五年级下册“因数与倍数”单元的学习属于初等数论的范畴，学生在学习本单元概念时存在一定的困难，主要原因是：第一，概念抽象，在学生看来“差不多”的概念比较多;第二，概念间的联系非常密切，学生理解和把握概念间的“逻辑”关系有困难;第三，学生很难在实际生活中找到表征概念的模型，“联系生活实际”学习数学的路走不通了;第四，由于专业知识储备不足，教师“讲不清楚”导致学生理解困难。笔者思考，要使学生能深c刻理解概念，正确把握概念之间的关系，教学时应该侧重体悟性的分析与计算，避免纯粹逻辑的演绎推理。基于此，让学生在直觉主义理论指导下，经历公倍数和最小公倍数概念的构造过程，精准回归倍数和因数作为“数”的身份特质，抓住它们表征数与数之间的“关系”的功能进行教学，让学生在不断体验中找准思考的着力点，不失为一条促使学生理解、掌握和运用概念的新路径。

二、实施准备

在数学概念的形成与发展中，人类的直觉起着至关重要的作用。直觉主义哲学高度重视“直觉”和“个人思维”在概念形成中的作用[2]，摈弃逻辑主义与形式主义对已有数学成果的“静态的”分析与“形式化”处理，认为攀附于语言的逻辑与形式化方法不能成为数学概念的基础。相反，数学是心灵的创造，是一种自由的思维活动[3]。据此，我们不难发现，“直觉体悟”指从具体、不同质的数的特征中构造出抽象的数学概念，它意味着数学概念需要建立在一种非经验主义的传统之上[4]。直觉主义学派认为只有通过直观感知，人类才得以认识到先天的数学概念。直觉主义哲学观使得在概念教学中，“让学生通过感性的直观体悟以认识先天的数学知识与概念”成为可能。下面，就以苏教版五年级下册“公倍数和最小公倍数”一课的教学为例，阐述“直觉体悟”贯穿数学概念教学的实施过程，以真正实现数学概念的被构造。

（一）直觉体悟目标的研制

有人说，数论是数学中的皇后。这句话揭示了数论知识在数学理论中的“原理”性的地位。让五年级的学生弄懂原理性概念并学会“数学地思维”，教学的目标定位很重要。直觉主义哲学观对学生数学学习在教学法方面最突出的指导意义是在让学生自己构造概念并在此过程中理解概念存在的意义和价值。因此，直觉主义指导下的学习目标研制就必须体现过程性、建构性。笔者认为，小学阶段学数论，就是要让学生在具体的情境中“论数”，论一论数的特点、构成、作用，论一论数与数之间的关系。以“公倍数和最小公倍数”一课的教学为例，教学目标就可作如下定位：（1）让学生在游戏中构造公倍数和最小公倍数概念，探索找公倍数和最小公倍数的一般方法。（2）在观察、比较、概括和抽象等数学活动中体悟数的特征。（3）在知识的沟通联结中体会数学是无限的科学。重点：构造公倍数和最小公倍数概念，体会公倍数和最小公倍数的特点。

（二）直觉体悟方法的应用

如前所述，直觉主义指导下的学生数学学习方法是构造和体悟。做好概念教学的选材立序工作，是帮助学生顺利实现概念构造的基础工程。苏教版“公倍数和最小公倍数”教材首先让学生通过“铺满”正方形的活动体会公倍数的意义，再让学生掌握通过列举倍数确定公倍数的方法。笔者思考：“铺满”正方形的操作活动和前面“公因数与最大公因数”的“分完”正方形的操作活动看似相同，其实不同，旧有的活动经验对本节课的操作活动无疑会产生干扰（就笔者多年的课堂观察发现，学生始终分不清“刚好分完”和“刚好铺满”这两种操作活动背后对应的数学原理），这是其一。其二，曹培英先生指出，有一些数学知识适合先从现实原型引入，然后从数学内部揭示生成该知识的原动力;也有些数学知识适合先在数学范围内讨论，然后应用于解决实际问题。例如，两个数的公因数和公倍数以及解方程等。[5]确实，教学实践表明从数学外部的现实情境引入公倍数和最小公倍数概念，学生从实际问题抽象出数学模型的难度很大。第三，数论是“纯粹数学”，“纯粹数学”如何避免抽象和枯燥，让学生亲近和喜欢？笔者以直觉主义数学哲学为理论指导，追溯数论知识的起源，设计以游戏的方式激发学生学习的乐趣，在游戏中自然地认识公倍数和最小公倍数，体会它们的特点，通过“游戏升级”实现“分散难点，各个击破”，取得了很好的教学效果。

三、策略分析

（一）以经历“构造概念”的过程为依托

直觉主义认为，只有基于主观直觉的或心智上的可构造性，数学概念和数学推理才能十分清楚地呈现在我们面前。直觉主义把人类的数学创造性活动分为不可分离的两个阶段，即原始直觉和从原始直觉出发的构造。

1.唤醒“原始直觉”

直觉主义认为数学学习的过程就是“借助构造一个实体，去构造另一个，再另一个”的过程;这种构造最重要的构件是一个清晰直观的概念。以公倍数和最小公倍数为例，它的构件就是“倍数”的概念。因此，教师在教学中首先就要帮助学生找到“构件”。

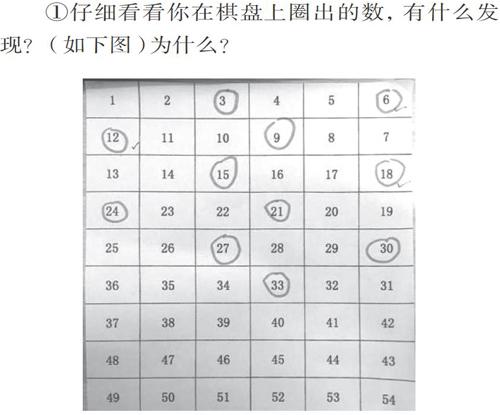
（1）微视频播放“跳格子”游戏：每个学生按抽到的指令（如，我每次跳2格）“跳格子”并用笔圈出棋子经过的数。

（2）学生游戏后组织交流：

①仔细看看你在棋盘上圈出的数，有什么发现？（如下图）為什么？

②其他同学圈出的数和所跳的格数之间是不是“倍数”关系？

2.构造新的“对偶”

直觉主义认为，数学构造行为是理性的一种直觉能力：人们在认识了当下的事物后，经过一段时间，注意力聚焦到另一事物上，即在已经完成构造①的基础上，人们重新获取新的知识，完成构造②，①和②在认识领域里就形成了一个原始对偶。当人们在时空中不断重复这种构造行为时，可以进一步获得新的“对偶”。以公倍数和最小公倍数为例，教师在唤醒学生已有的倍数概念的基础上，先行组织学生观察、比较自己与他人棋盘的差异，实现学生从“倍数”到“公倍数”概念的初步构造;接着组织“寻找公倍数”的认知活动，实现学生对“公倍数”的再次构造;再组织学生观察“公倍数之间的关系”“创造公倍数队伍”“改造公倍数队伍”等活动，实现从“公倍数”到“最小公倍数”概念的构造。从倍数到公倍数，再到最小公倍数，学生在有序的认识活动中获得了完整、清晰的公倍数和最小公倍数的概念。

（二）以体悟概念之间的“关联性”为基础

直觉主义认为数学概念来自“心灵的构造”，一个概念总是在原有概念的基础上被构造出来，这也直接表明直觉主义认为数学对象之间密切联系的直觉主义逻辑观。在直觉主义哲学观指导下的数学概念教学，必须让学生充分体会概念的关联性。

1.概念的意义关联性

概念在意义上的关联性是指尽管两个概念包含的对象的数量不同，但它们在意义上是有联系的。以公倍数和最小公倍数为例，教学中教师要让学生体会到：公倍数和最小公倍数都是倍数，它们都表示两个数倍数中重叠的部分。

2.概念的生长关联性

概念的生长关联性是指一个概念在另一个概念的基础上发展、变化而来，有时，这两个概念是包含关系，如：最小公倍数和公倍数、方程和等式，有时，还指一个概念是另一个概念产生的“副产品”，如：最简分数之于约分、互质数之于公因数等等。以“公倍数和最小公倍数”为例，教学中教师让学生体会到：（1）公倍数和最小公倍数都建立在倍数概念基础上;（2）最小公倍数建立在公倍数概念基础上，是概念从一般走向了特殊。怎样把这样枯燥复杂的关系生动有趣地呈現给学生，让学生接受，甚而至于“喜欢”上它们呢？孩子是天生的游戏者，教学中可以通过设计目标明确的游戏活动，让学生充分体会公倍数和最小公倍数的特征。比如，初次游戏，观察圈出的数的特点，唤醒倍数关系;再次游戏，找两个棋盘里相同的数，感悟公倍数的“共性”;第三次游戏，通过猜学生所说的公倍数一词“该怎么写”，采访“你怎么想到起这个名字”等等，促使学生把公因数和最大公因数的学习经验主动地迁移过来，让学生体会知识方法结构的关联性;最后，观察一列有序排列的公倍数，体会公倍数和最小公倍数的倍数关系，让学生体会到公倍数的敏感易变。通过这样的数学活动，公倍数和最小公倍数就从一个个冰冷的数变成了有温度、有生命活力的学生的“伙伴”了。

（三）以体悟概念外延的“无限性”为关键

让我们先来看下面两个教学片段：

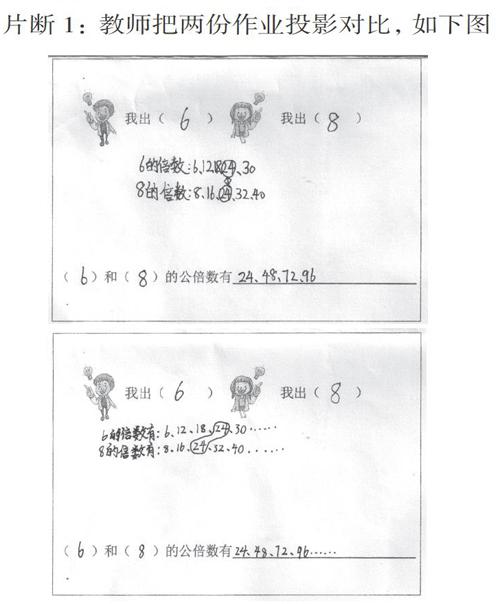
片断1：教师把两份作业投影对比，如下图

教师提出问题：

（1）比较这两份作业，你发现了什么？

（2）公倍数的后面写上省略号，什么意思？

（3）你怎么知道公倍数的个数是无限的？你能找出下一个吗？

（4）假如两个数的公倍数里有一个是10，你能写出它们其他的公倍数吗？

片断2：出示一个由若干个完全相同的小长方形拼成的正方形棋盘，组织学生找正方形并交流：

（1）你怎么知道正方形的边长是6厘米？你还能找出多大的正方形？

（2）这么多的正方形，我们说不完，看不尽，但是我们可以想得到。谁帮了我们的忙？

数学在很大程度上被定义为“无限的科学”。小学数学教学的一个重要目标，即是帮助学生逐步发展起无限的观念。无限性是直觉的场所，直觉在学生建立对数学的潜无限认识的过程中发挥着巨大的作用。上述教学片段中，呈现两份对比性作业，通过讨论“省略号能不能加”的问题，让学生体会公倍数有无数个;接着，通过“找正方形”的活动，在数形结合的思辨活动中充分发展了学生的想象力，让他们在可重复的学习行为中“看到”并相信了无限。

（四）以体悟概念本体的“有用性”为目标

直觉主义尽管认为数学是心灵的创造，但它不否认新的数学概念的建立于人们进一步认识数学的积极作用。因此，教学中让学生在观察比较中体会数的“有用性”就是我们的课堂教学必须关注的目标之一。还以公倍数和最小公倍数为例，学习公倍数和最小公倍数到底有什么用？教学中，教师可以多组织充分的观察、比较、思辨活动，让学生体会公倍数和最小公倍数的作用。比如，知道两个数有公倍数10，让学生猜其他的公倍数，讨论会不会出现公倍数5，让学生深刻体会认识学习最小公倍数的价值;再如，让学生观察“棋盘中有什么图形？正方形的边长为什么是6厘米？你看不到但能想得到的正方形还有哪些？比较公倍数和最小公倍数，你喜欢哪一个？为什么？……”让学生充分体会公倍数和最小公倍数的作用和价值。在此过程中，数形结合、极限等数学思想得到了渗透，还帮助学生充分体会到了“数学的自由创造和想象”，感受到了数学思维的力量。

在直觉主义哲学观的指导下，通过丰富多样的直观体验活动让学生去构造概念，帮助学生实现对概念内涵的真理解，并在此过程中让学生体会数学活动、领会数学思维、增强学习兴趣、培育理性精神，是小学数学课堂教学的应有之义。

参考文献：

[1]张景中.数学与哲学（典藏版）[M].北京：中国少年儿童出版社， 2011：82.

[2]冯棉.论数学哲学中的直觉主义思想[J].华东师范大学学报（哲学社会科学版）， 2002，34（7）：35.

[3]DR. L. E. J. Brouwer. Intuitionism and formalism[J]. Bulletin of the American Mathematical Society， 1999，37（1）：55.

[4]高劍，黄祖宾.数学哲学中的直觉主义[J].自然辩证法研究， 2013，29（12）：10.

[5]曹培英.跨越断层，走出误区：“数学课程标准”核心词的实践解读之八——模型思想（下）[J].小学数学教师， 2015（2）：6.

责任编辑：丁伟红

Intuitive Perception： A New Path to Acquiring Concepts

ZHANG Xiaoxia

（Yancheng Tinghuxinqu Experimental Primary School， Yancheng 224001，China）

Abstract：  The mathematical concept is the abstract entity of humans thinking creation. Intuitive philosophy particularly emphasizes the role of humans intuition in mathematic concepts and holds that pure intuition is the basic ground for the generation of mathematical concepts. Taking the teaching of common multiple and minimum common multiple as examples， teachers should help students construct the concepts in the process of perception with accurate regression of multiples and factors as the identity of “numbers”. Meanwhile， teachers should implement teaching by grasping the relationship between representative numbers and numbers， which is key in promoting students understanding， mastering and applying mathematical concepts.

Key words：  intuitive perception; mathematical concept; primary school mathematics teaching