一类恶性肿瘤增长模型的稳定性分析
王国波
太原科技大学应用科学学院,山西 太原 030024
癌是医学上对恶性肿瘤的一种通称.癌细胞几乎可以影响到身体的每个器官,其主要特点是可以使得正常细胞失去调节生命的能力.这种现象使它们能够超越正常的界限,侵入周围的组织和器官而导致患者死亡,医学上称之为癌症扩散.
近几年,数学模型成为数学家和生物学家研究癌症复杂动力学行为的主要工具之一.癌症数学模型建立的过程必须和临床结果、实验数据相吻合,同时也要考虑肿瘤细胞和免疫细胞之间的相互作用.这种复杂的模型过程数学家主要利用微分方程进行建立,通常是常微分方程和时滞微分方程对模型加以刻画和描述.文献[1~6]对癌症以及关于癌症所建立起来的数学模型做了大量有意义的工作.
De Pillis LG和Radunskaya A在文献[7]中建立了恶性肿瘤模型:
(1)
其中,T(t)表示t时刻肿瘤细胞的密度;N(t)表示t时刻健康的宿主细胞的密度;I(t)表示t时刻单个肿瘤间隔区的效应免疫细胞密度;ri(i=1,2)分别表示肿瘤细胞和健康细胞在忽略其他细胞对其影响下的增长率;ki(i=1,2)分别表示肿瘤细胞和健康细胞的最大承载量;a13表示免疫细胞对肿瘤细胞的杀伤率;a21表示肿瘤细胞对健康细胞的灭活率;a31表示肿瘤细胞对免疫细胞的灭火率;d3表示免疫细胞的正常死亡率;a12,r3,k3分别表示正常数.文献[7,8]利用局部紧不变集方法(LCIS)得到模型中肿瘤细胞消除的充分条件和肿瘤细胞不受约束下平衡点的全局稳定性.
本文在文献[7]的基础上研究在免疫细胞死亡这一极端条件下的肿瘤细胞和健康细胞的动力学行为,以便更好地分析肿瘤细胞扩散的复杂过程.文章主要对肿瘤细胞和健康细胞模型平衡点稳定性进行了定性分析,并给出模型在正平衡点处经历Hopf分支的条件.
1 模型在x3=0限制条件下的稳定性分析

(2)
为了更好地理解系统(2)在最大不变集上解轨迹的情况,我们假设x3=0.于是方程(2)变为
(3)
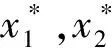
(A1):r2>a21,1>a12.
(A2):r2 下面我们接着分析方程(3)在四个平衡点处稳定性以及Hopf分支存在性.以此,我们假设 则方程(3)的线性化方程为 其中 定理1若(A1)成立时, 在平衡点Si(i=1,2,3)处不稳定. 证明 当S=S1时,方程(3)在S1处对应线性化方程的特征方程为 (1-λ)(r2-λ)=0 于是得λ1=1>0,λ2=r2>0所以方程(3)在S1处不稳定.同理方法我们可以同样处理S2,S3. 在条件(A1)成立时,对于S=S2,可得到其对应特征方程的根为λ1=1>0,λ2=r2-a21>0,所以方程(3)在S2处不稳定. 对于S=S3,可得到其对应特征方程的根为λ1=a12-1>0,λ2=-r2<0所以方程(3)在S3处不稳定.证毕. 定理2方程(3)满足如下: (i)当A1(r2)>0,A2(r2)>0时,方程(3)在S4处渐近稳定; (ii)当(A1),(A3)~(A5)成立时,方程(3)在S4处产生Hopf分支. 证明 当S=S4,可得到其对应特征方程为 λ2+A1(r2)λ+A2(r2)=0 (4) 其中 于是得 利用Routh-Hurwotz[9]准则法可得出,当A1(r2)>0,A2(r2)>0时,方程(4)的所有根都具有严格负实部,则有方程(3)在S4处渐近稳定. 同时满足 (a)方程(3)在t-x1坐标下的波图(b)方程(3)在t-x2坐标下的波图 图1 方程(3)在特定参数下数值解 (c) 方程(3)在x-y坐标下的相图(d)(c)在(1,0)处局部放大图 图2 方程(3) 的相图 本文主要利用常微分方程的定性理论分析了恶性肿瘤增长模型平衡点处的稳定性并给出系统产生Hopf分支的条件,同时数值模拟得出方程的解收敛到死亡平衡点.然而,此模型在参数变化情况下还有许多更有意义的分支现象,它们将可能在医学上对癌症治疗方案产生积极的意义,这些问题有待于进一步的分析和研究.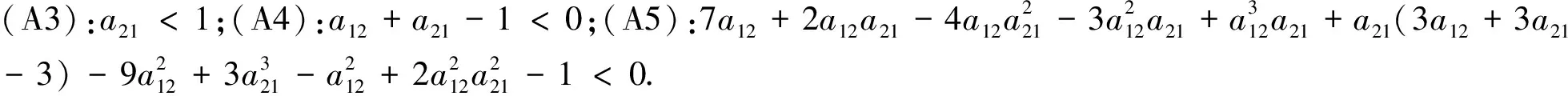
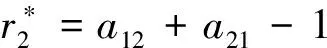
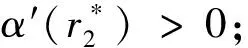


2 数值仿真


Fig.1 Simulated solution of equation (3)
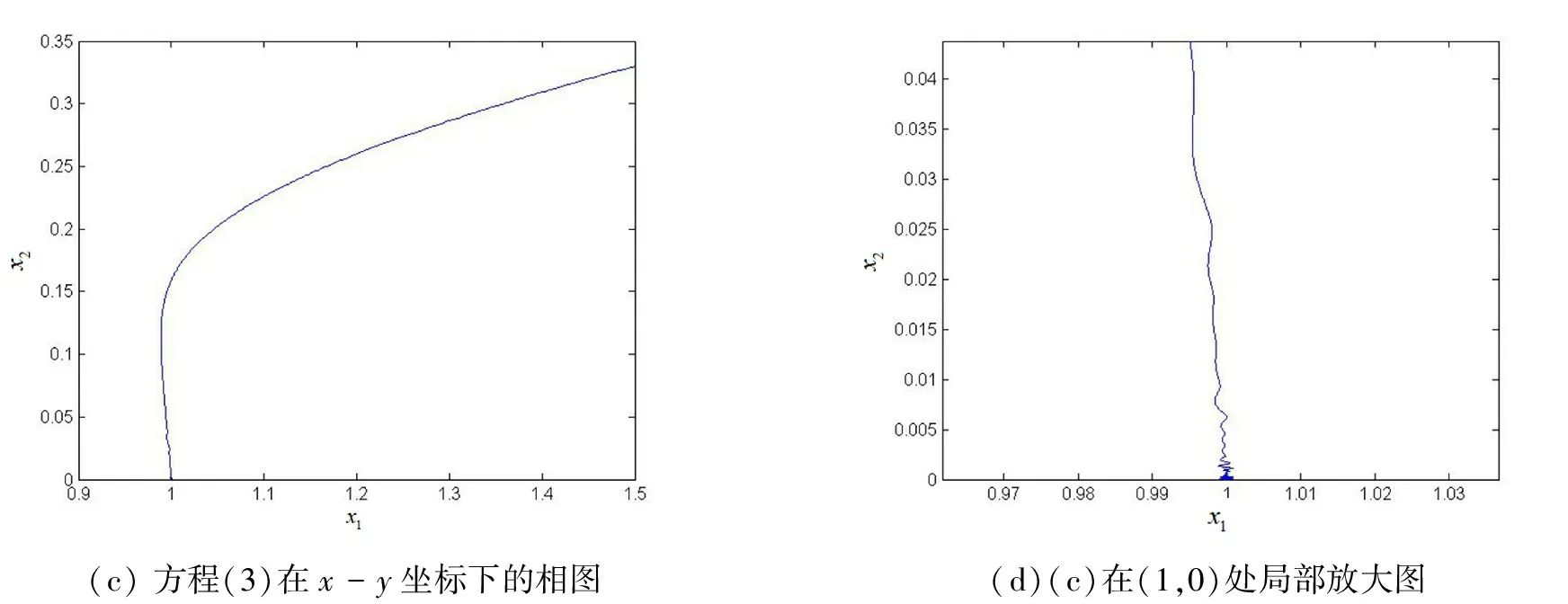
Fig.2 Phase plots for equation (3)3 结语

