非等时距灰色模型在冻土路基沉降预测中的应用

马争锋,王青志

(1.青海民族大学 交通学院，青海 西宁 810000；2 青海省交通科学研究院, 青海 西宁 810008)

青藏公路起于青海西宁，终于西藏拉萨，全长1 937 km，路基宽10 m，坡度小于7 %，是G109线的一部分。它的平均海拔高度超过4 500 m。青藏公路于1950年动工，1954年通车，1974年开始全面改建，并将公路标准提高为二级，同时加铺沥青路面，1985年8月全线黑色路面铺筑工程基本竣工。青藏公路的病害中85 %是融沉造成的，15 %是冻胀和翻浆所致[1]。青藏公路的修筑与运营，改变了路基下多年冻土的温度状况，也改变了地基土的受力状态，必然引起路基的热学和力学稳定性发生变化，从而导致路基产生沉降变形[2]。为研究青藏公路路基沉降变形特性，在G109线的K2967+850处设置了监测断面。

灰色系统理论是一种研究“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定性问题的新方法，并依据信息覆盖，通过序列算子的作用探索事物运动的现实规律，其特点是“少数据建模”[3-6]。由于影响冻土路基沉降的因素是不可控的，而且同一因素在不同时段和不同区域对冻土路基沉降的影响程度也不一样，所以，冻土路基沉降与其影响因素之间构成了一个灰色系统[7]，可以采用灰色系统理论进行预测。目前，用灰色系统理论对青藏高原冻土路基进行沉降预测的比较少，针对2004年以前冻土路基工后沉降值成指数变化的，研究主要采用的是传统的GM(1，1)灰色预测模型，预测精度较高。但是，2012年11月～2014年3月青藏公路K2967+850监测断面处冻土路基中6处沉降板的累计沉降监测数据显示出了较大的周期性和波动性，并没有呈指数变化。根据马巍等[8-9]的研究，冻土路基沉降监测数据在2004年之后就不呈指数型变化，而出现周期性和波动性，这也证明青藏公路冻土路基出现周期性和波动性沉降的合理性。在采用传统的等时距GM(1，1)灰色预测模型直接预测不合理的情况下，本文采用非等时距GM(1，1)灰色预测模型[10-11]对累计变形曲线的上下边界分别建模预测。同时根据建模结果，将预测模型的模拟值序列与实测值序列进行对比，判断模型的模拟精度。在精度达到要求的情况下，用此模型对K2967+850监测断面冻土路基的累计沉降变形量进行极限预测，并计算极限变形过程中的变化幅值。

1 非等时距GM(1，1)灰色预测模型

1.1 建模步骤

由于现场数据监测时间间隔是不等时距的，所以采用非等时距的GM(1，1)灰色预测模型把原始的非等时距时间间隔序列转换成等时间间隔序列，按等时距GM(1，1)模型进行数据处理。

冻土路基沉降监测数据的采集时间间隔序列(单位：d)为：

Q(0)={Q(0)(1)，Q(0)(2)，…，Q(0)(n)}。

对该序列进行一次累加生成累计时间的新序列：

Q(1)={Q(1)(1)，Q(1)(2)，…，Q(1)(n)}。

实测的冻土路基单次沉降量序列(单位：mm)为：

S(0)={S(0)(1)，S(0)(2)，…，S(0)(n)}。

对该序列进行一次累加生成累计沉降量的新序列：

S(1)={S(1)(1)，S(1)(2)，…，S(1)(n)}。

按照灰色系统的建模方法，可以得到一个一阶线性动态微分方程：

(1)

根据最小二乘法原理，可得参数列：

(2)

(3)

yn=[S(0)(2)，S(0)(3)，…，S(0)(n)]T，

(4)

(5)

式(5)称为全信息的非等时距GM(1，1)模型。

1.2 模型后验差检验[11-12]

1.2.1 原始数据

原始数据的平均值：

(6)

原始数据的修正方差：

(7)

原始数据的均方差为S1。

1.2.2 残差

预测求解后还原数列：

(8)

残差：

(9)

残差的平均值：

(10)

残差的修正方差：

(11)

残差的均方差为S2。

1.2.3 模型精度分级标准值

均方差比值为：

(12)

小误差概率：

(13)

按照C与p计算的结果，查看表1模型精度分级表，评定模型的精度。

表1 模型精度分级表

2 工程实例分析

2.1 沉降监测断面概况

G109线K2967+850沉降监测断面位于青藏高原腹地的楚玛尔河高平原，此处有严寒、半干旱的大陆性气候，年平均气温约-6 ℃，年降水量小于300mm，降水多集中在6月～9月，存在大片多年冻土区。监测断面所在公路为东西走向，路基南、北坡分别为阳坡、阴坡，左右路肩分别高2m。在左右路肩深度2m处分别埋设了沉降板1和2进行沉降变形观测。

2.2 监测数据分析与建模

2.2.1 监测数据分析

以2012年5月8日的2个沉降板处各自的标高为起始观测高度，各个沉降板处观测到的10组由实测标高转换成的单次变形量数据如图1所示。图1中的单次变形量中的正值表示路基下沉，负值表示路基冻胀。由于非等时距的GM(1，1)模型采用的都是非负序列，所以需要对每个沉降板处10组单次变形量序列进行累加处理(图2)。图2显示累计沉降量随天数的增加而呈现周期性波动，但是四年多的观测结果显示出沉降板1和沉降板2都具有下降趋势。通过图2可以计算出沉降板1累计沉降变形的平均变化范围是3.34mm，沉降板2的累计沉降变形的平均变化范围是2.18mm，这反映出阳坡的冻胀融沉程度大于阴坡，也间接说明了阳坡路基的稳定性比阴坡路基差。

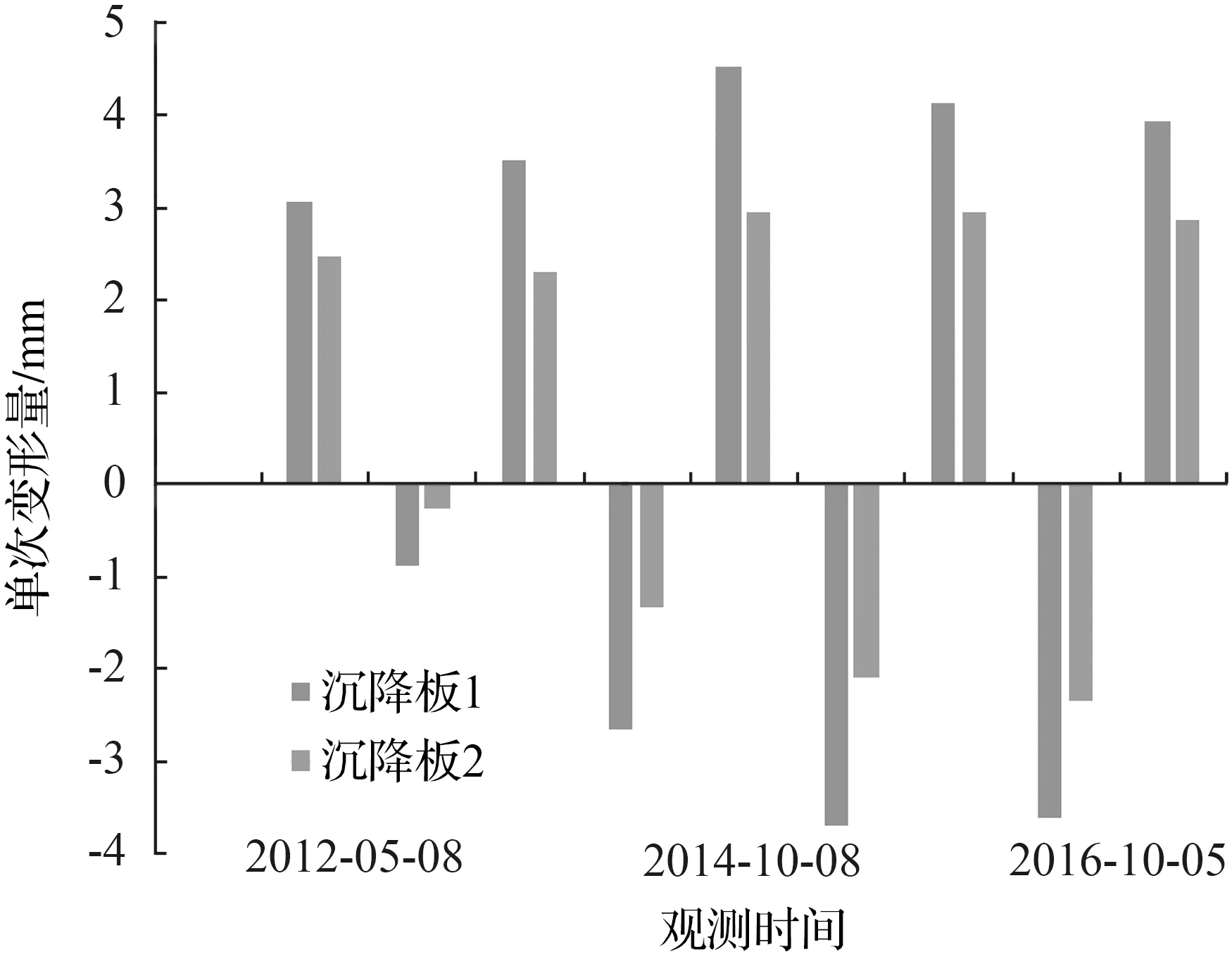
图1 单次变形量随观测时间变化图

Fig.1 Change of single deformation with observation time

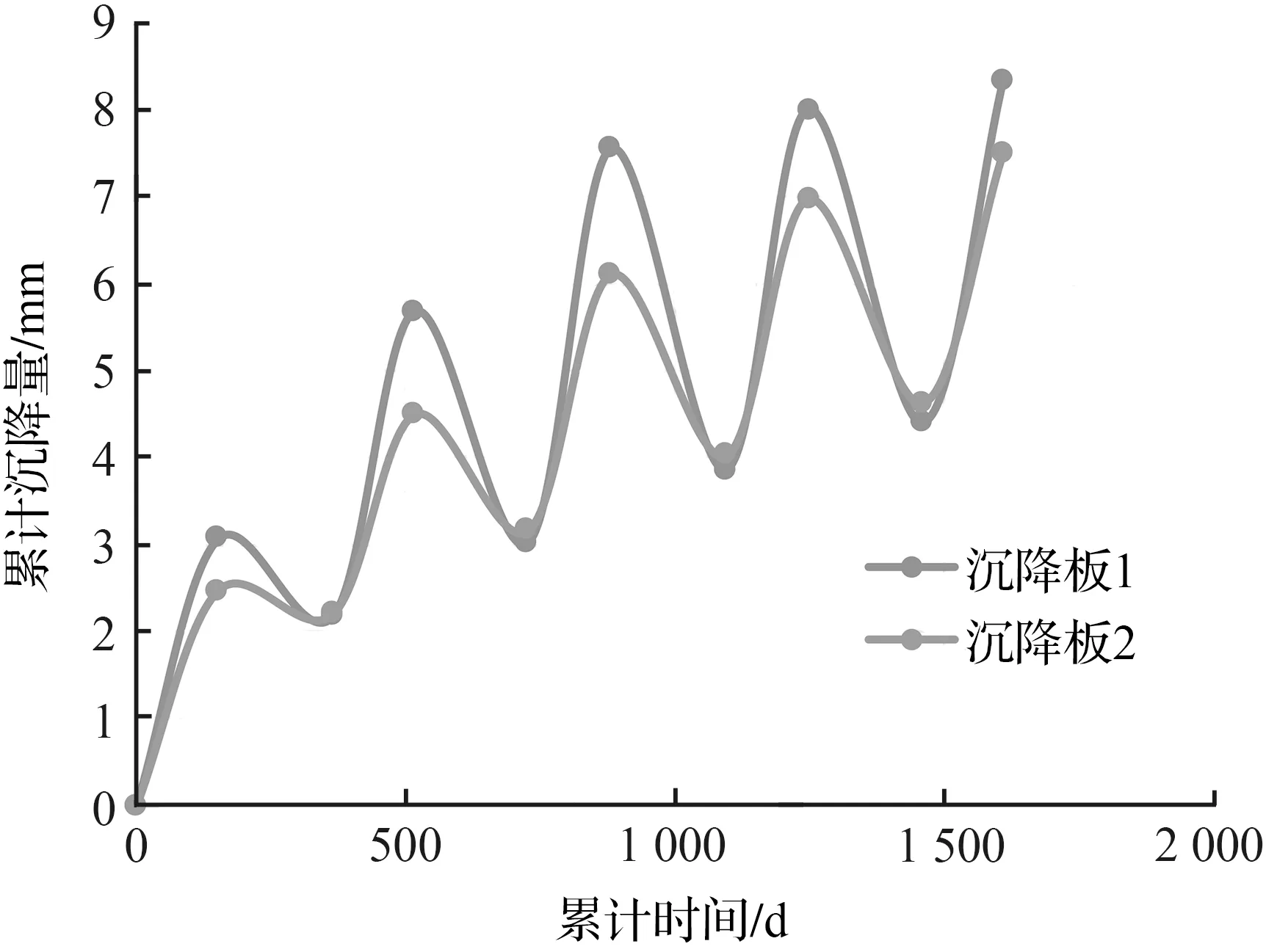
图2 累计沉降量随累计时间变化图

Fig.2 Changes of cumulative settlement with cumulative time

2.2.2 建立冻土路基沉降预测模型

如图2所示，累计沉降量随天数增加而出现周期性波动情况。受当地周期性波动气温的影响，当年的5月至9月，冻土路基融化下沉，当年的10月至次年的4月，冻土路基处于冻胀阶段。由于非等时距GM(1，1)灰色预测模型实质上是用一条指数曲线来拟合原始序列[13]。所以无法直接使用所有的波动性数据进行建模预测。通过分析可知，累计沉降量随天数增加而出现周期性波动的过程存在上下边界，所以分别对波动曲线的上边界和下边界分别进行建模预测是可行的。

冻土路基两个沉降板沉降监测数据的采集时间间隔序列(单位：d)为：

对上面两个序列分别进行一次累加生成累计时间的新序列：

实测的冻土路基单次沉降量序列(单位：mm)为：

对上面四个序列分别进行一次累加生成累计沉降量的新序列：

基于式(1)至式(5)，求出冻土路基非等时距GM(1，1)灰色预测模型的关键参数a和b及拟合精度，具体见表2。

表2 非等时距GM(1，1)灰色预测模型关键参数及拟合精度

通过关键参数a和b可以得到沉降板1和2的四个非等时距GM(1，1)灰色预测模型，如下所示：

① 沉降板1，10月份：

(14)

② 沉降板1，5月份：

(15)

③ 沉降板2，10月份：

(16)

④ 沉降板2，5月份：

(17)

通过式(14)至式(17)四个预测模型，可以得到对应于已知监测时间的累计沉降量的拟合值：

将累计沉降量的实测值和拟合值代入式(6)至式(13)进行精度检验。所有模型的精度检验指标C和p的具体数值见表2。表2显示四个模型的拟合精度为I级。图3展示了模拟值与实测值得对比情况，实测值和拟合值十分接近。所以，可以用已建立的模型对监测路基的沉降规律进行长期预测。

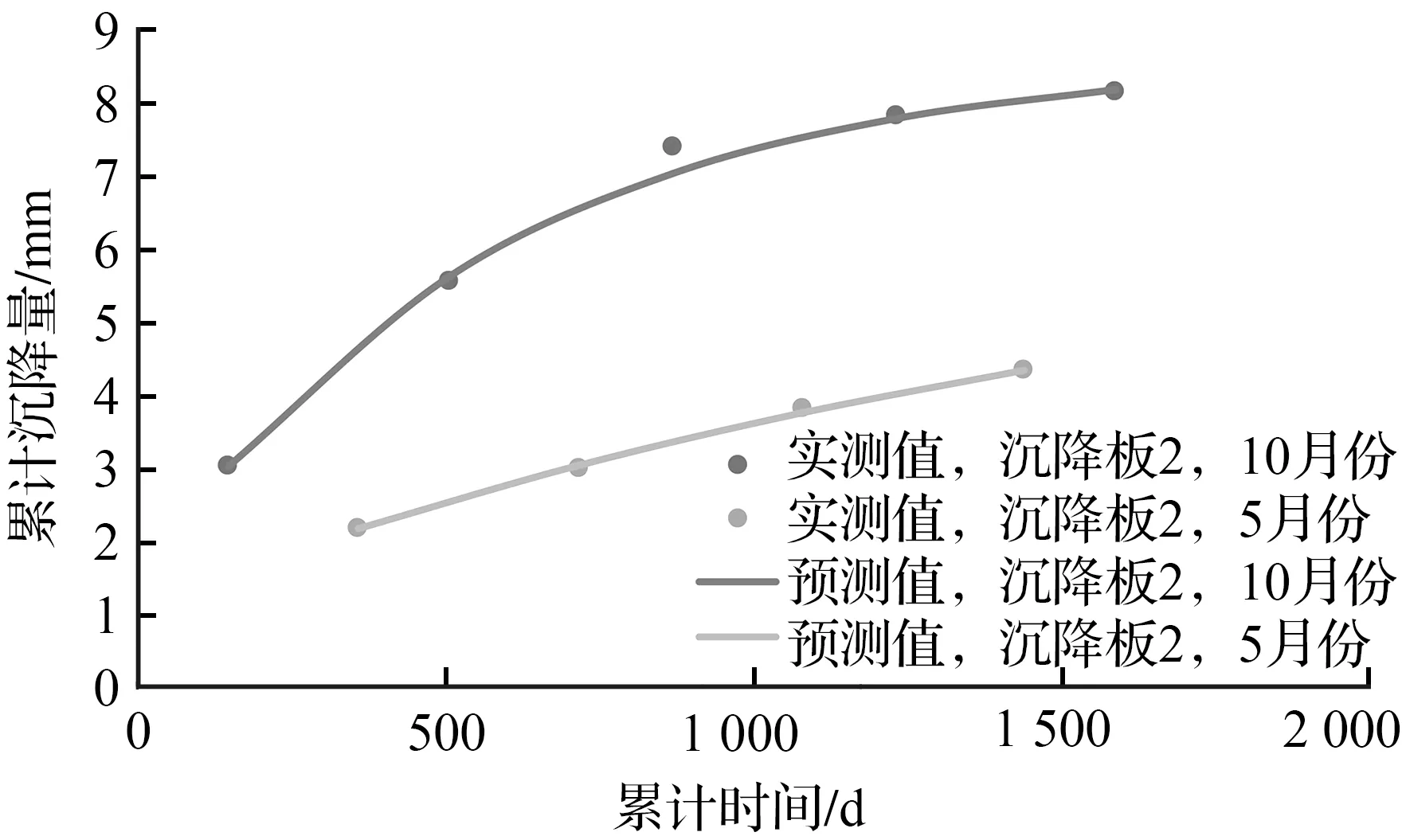
(a)沉降板1

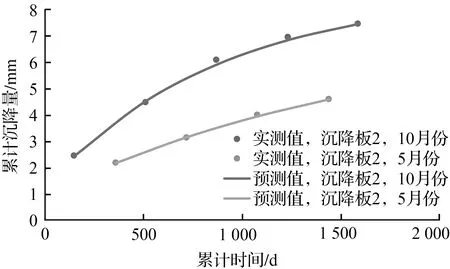
(b)沉降板2

图3 实测值与非等时距GM(1，1)灰色预测模型模拟值对比图

Fig.3 Comparison between measured values and simulated values of non-isochronous GM(1,1)gray prediction model

由式(1)～(14)可知，当Q(1)(k+1)趋于正无穷大时，极限累计沉降量为8.85 mm。由式(1)～(15)可知，当Q(1)(k+1)趋于正无穷大时，极限累计沉降量为7.12 mm。由式(1)～(16)可知，当Q(1)(k+1)趋于正无穷大时，极限累计沉降量为8.78 mm。由式(1)～(17)可知，当Q(1)(k+1)趋于正无穷大时，极限累计沉降量为7.34 mm。所以，阳坡极限累计沉降量的上边界值为8.85 mm，下边界值为7.12 mm，稳定变化幅值为1.73 mm。阴坡极限累计沉降量的上边界值为8.78 mm，下边界值为7.34 mm，稳定变化幅值为1.44 mm。

阳坡路基的极限波动幅值大于阴坡路基的极限波动幅值，左右路基的差异变形，会导致左右路面的严重不平顺性。由于很难保证后期路基的变形监测不会遇到异常情况，所以随着日后监测数据量的增加，会继续修正极限预测结果。这对冻土路基长期变形监控及重点维修将起到至关重要的作用。

3 结论

① 四年多的实际监测数据显示监测路基左右路肩下2 m深度处的累计沉降量随天数的增加而呈现周期性波动，但左右路肩的变形都呈现出下降的趋势。左右路肩下2 m深度处的累计沉降量的周期性波动差异反映出阳坡的冻胀融沉程度大于阴坡，也间接说明了阳坡路基的稳定性比阴坡路基差；

② 使用非等时距GM(1，1)灰色预测模型对两个路基监测点的累计沉降量建立了预测模型，该预测模型的拟合精度都达到了I级，说明采用该预测模型对G109线K2967+850监测断面2 m深度以内冻土路基的沉降预测是可信的；

③ 阳坡极限累计沉降量的上边界值为8.85 mm，下边界值为7.12 mm，稳定变化幅值为1.73 mm。阴坡极限累计沉降量的上边界值为8.78 mm，下边界值为7.34 mm，稳定变化幅值为1.44 mm。因此，阳坡路基的极限波动幅值大于阴坡路基的极限波动幅值。这也说明随着时间的增加，左右路肩会形成稳定的差异变形。