斜放网格棱柱面密肋折板网壳的静力特性分析

朱锐，张华刚*，陈寿延，姜岚,2，唐攒辉

(1.贵州大学 空间结构研究中心，贵州 贵阳 550003；2.湖南大学 土木工程学院，湖南 长沙 410012)

0 引言

当下空间结构的发展形势是轻质高强，但随着我国经济发展，各国对建筑结构耐久性和经济性的需求提升较大[1]。基于以上变化，国内专家对混凝土开展了一系列的研究，主要是因为混凝土结构相比于钢结构在耐久性和中小跨度空间结构中的经济性有着无可比拟优势。为了克服混凝土自重大的劣势，建筑专家开始对可跨越跨度较大的混凝土壳体结构开展研究：于2009 年建成的华南理工大学体育馆采用预应力混凝土双曲抛物面组合扭壳[2]，但此类结构的支模过程繁琐，经济性不佳。相比而言，折板壳和混凝土网壳可有效克服这一缺点，刘国葵将V形折板弯曲为拱形，应用于跨度为30m的工程中，这一创新成果使得V形折板的跨度进一步加大[3]。同时，钢—混凝土组合结构是壳体结构当前重要发展方向之一[4-5]，滕锦光等为降低混凝土壳体施工难度，在混凝土壳下方增加一个带肋钢壳，此预制带肋钢壳既为承力结构，又是混凝土壳体的模板[6-7]。与此同时，常玉珍团队开展了组合肋壳结构的研究，此结构将U型钢外包在混凝土带肋壳上，提高了带肋壳刚度以增加结构承载力，从而使结构跨越更大跨度[8]。若将混凝土壳板采用预制手段处理，则此结构可完全摒弃施工模板这一问题[9]。

在组合结构的思路下，考虑结合折板结构双向传力和密肋平板轻质高强的优点，张华刚等提出了混凝土密肋折板网壳结构，它由密肋平板在脊(谷)线处汇交构成[10]，此结构主要受力构件为梁系构件组成巨型网格，即由数个密肋平板构成，用于该结构的模板可模块化生产，支模较薄壳结构简便且构件受力特点较连续薄壳容易把握。其中人字形密肋折板网壳已成功应用于贵州关岭美食城等工程中，结构具有较佳的空间受力性能和良好经济指标[11]。此外，方强等还开展了拟扁网壳和幕形网壳的静动力性能分析，表明结构具有明确的传力途径和空间受力特征[12-15]。柳勇斌的分析表明正交正放网格棱柱面网壳可看作是由折线拱构成的单向传力结构，纵向脊线几乎不影响网壳整体刚度及承载力[16]。

为提高结构的空间受力效应，本文将网格斜放，以使密肋平板的荷载能分配至纵向脊线上，基于静力有限元基本理论[17]做结构静力特性分析，并考察主拱刚度、脊线刚度、斜向肋肋刚度、矢跨比、边梁刚度、屋面板厚度对结构静力特性的影响，以期为这种结构的工程应用提供参考。

1 结构形式及算例情况

1.1 结构形式

结构形式如图1所示，通过等分圆柱面来构造网壳，密肋平板的网格为斜交斜放网格，屋盖端部支承在山墙框架上。屋盖的推力需要由主拱脚下设置的抗推结构来平衡，抗推结构可采用纵向边梁连接，结构形式可为平面框架或抗推墙等，间距为B。屋盖的跨度为L，矢高为f。将图1(b)中延剖切符号I将结构剖开，其剖面图如图1(c)中所示。

(a)空间示意图

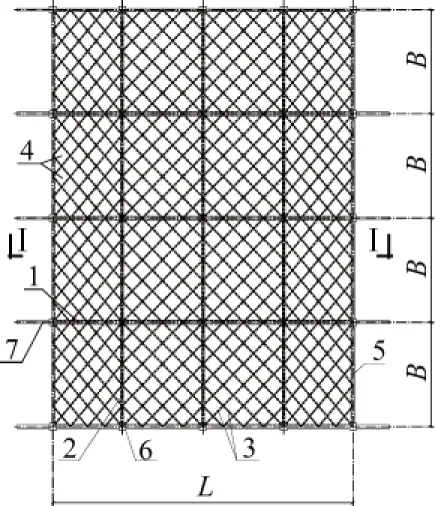
(b)平面示意图

(c)剖面示意图

1.2 算例情况及有限元模型

1.2.1 算例情况

取屋盖跨度为L=36 m，纵向长度为48 m，主拱间距B=12 m，全部算例的结构布置及密肋板的网格情况如图2 所示，图2中单位为 mm, 每段边梁被划分成5个网格，主拱每个折线被划分为4个网格，由于边梁和主拱的网格长度不一致，因此密肋平板网格斜交斜放。本文的全部分析算例情况如下：

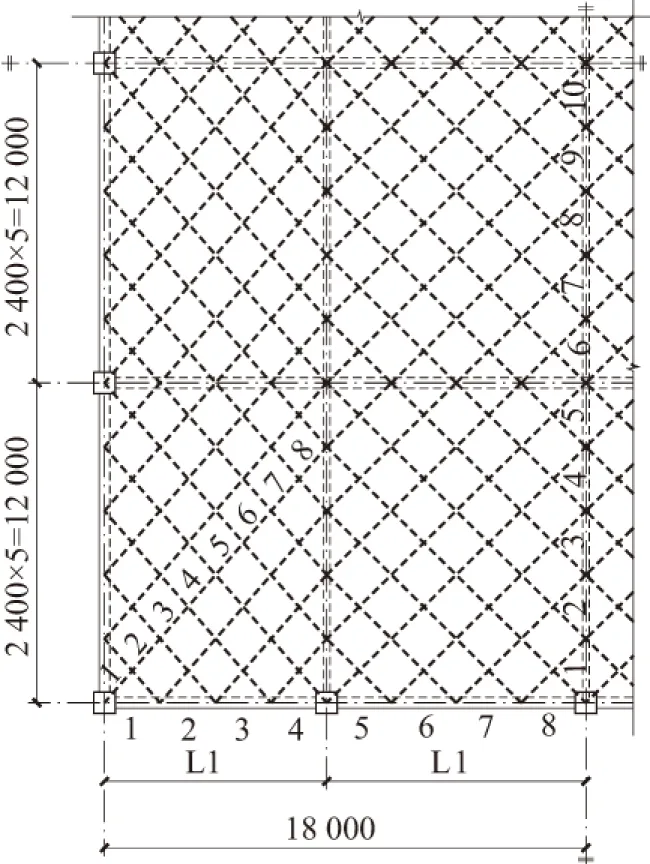
(a)结构平面

(b)网格示意图

(c)边梁截面

(d)主拱截面

(e)脊线截面

图2 算例情况(单位：mm)

Fig.2 Examples of cases(Uint：mm)

(1)基本算例。不考虑抗推支座影响做屋盖的静力分析，即计算时主拱拱脚按固支考虑。屋盖矢高f=7.2 m，密肋截面高度h=0.5 m，屋面板厚度δ=60 mm，主拱和边梁的截面高度hg和hL均取0.6 m，其截面宽度bg和bL均为0.4 m，脊线截面高度hJ=0.55 m，宽度bJ为0.25 m。山墙框架腹杆截面尺寸为0.4 m×0.4 m、中弦剖面截面尺寸均为0.4 m×0.5 m，下弦横截面尺寸为0.4 m×0.6 m。

(2)参数化分析算例。在基本算例基础上改变其单一变量来做结构挠度与内力影响的参数化分析：

① 改变结构的矢跨比分析5个算例，分别取屋盖矢高f=12.0、9.0、7.2、6.0、4.5 m，即结构矢跨比由1/3降低至1/8，以考察矢跨比对结构挠度与内力的影响。

② 取主拱及边梁的截面高度hg和hL均为1.0 m，脊线截面高度hJ=0.95 m，通过改变密肋截面高度以考察其刚度对屋盖挠度与内力的影响，且分别取h=0.5 m、0.6 m、0.7 m、0.8 m和0.9 m，相当于屋盖跨度的1/70～1/40。

③ 仅改变主拱的横截面高度hg以考察其刚度对挠度与内力的影响，且hg按0.1 m的级差由0.6 m增大至1.1 m，相当于hg取屋盖跨度的1/60～1/33，共计算6个算例。

④ 对于脊线刚度影响的算例，固定主拱截面高度hg=1.1 m，脊线的横截面高度hJ按0.1 m的级差由0.55 m增大至1.05 m，共计算6个算例。

⑤ 在基本算例基础上，仅改变边梁的截面高度hL计算5个算例，且hL按级差0.1 m由0.6 m增大至1.0 m，相当于hL取边梁自身跨度的1/20～1/12。

⑥ 仅分别取屋面板厚度δ=60 mm、80 mm、100 mm、120 mm计算4个算例，以考察屋面板厚度对屋盖挠度与内力的影响。

图3 屋盖的有限元模型

1.2.2 结构有限元模型

各梁系构件及山墙框架构件均采用空间梁单元，屋面板采用板壳单元，且考虑梁、壳单元的中性层重合下结构的静动力特性，有限元节点主要采用了自然节点，在主拱拱脚处固定约束了节点的全部位移。计算时将外荷载转换为质量，施加在有限元模型上，外加荷载均为3.35 kN/m2,此外加荷载满足恒活组合荷载的情况。混凝土的弹性模量取Ec=3×104N/mm2，泊松比取ν=0.2，其有限元模型如图3所示。

2 结构的静力性能分析

2.1 算例情况

取拱向结构的矢高为f=4.2 m，即矢跨比为1/5，将每个密肋平板的拱向均划分为4格，屋面板厚为60 mm，各构件的截面尺寸：主拱和端隔上弦为0.3 m×0.5 m、斜向肋梁为0.25 m×0.25 m、边梁为0.4 m×0.6 m、脊线为0.3 m×0.50 m，并编号如图4所示。通过有限元法分析结构的弹性静力性能。

2.2 计算结果与分析

2.2.1 结构的变形情况

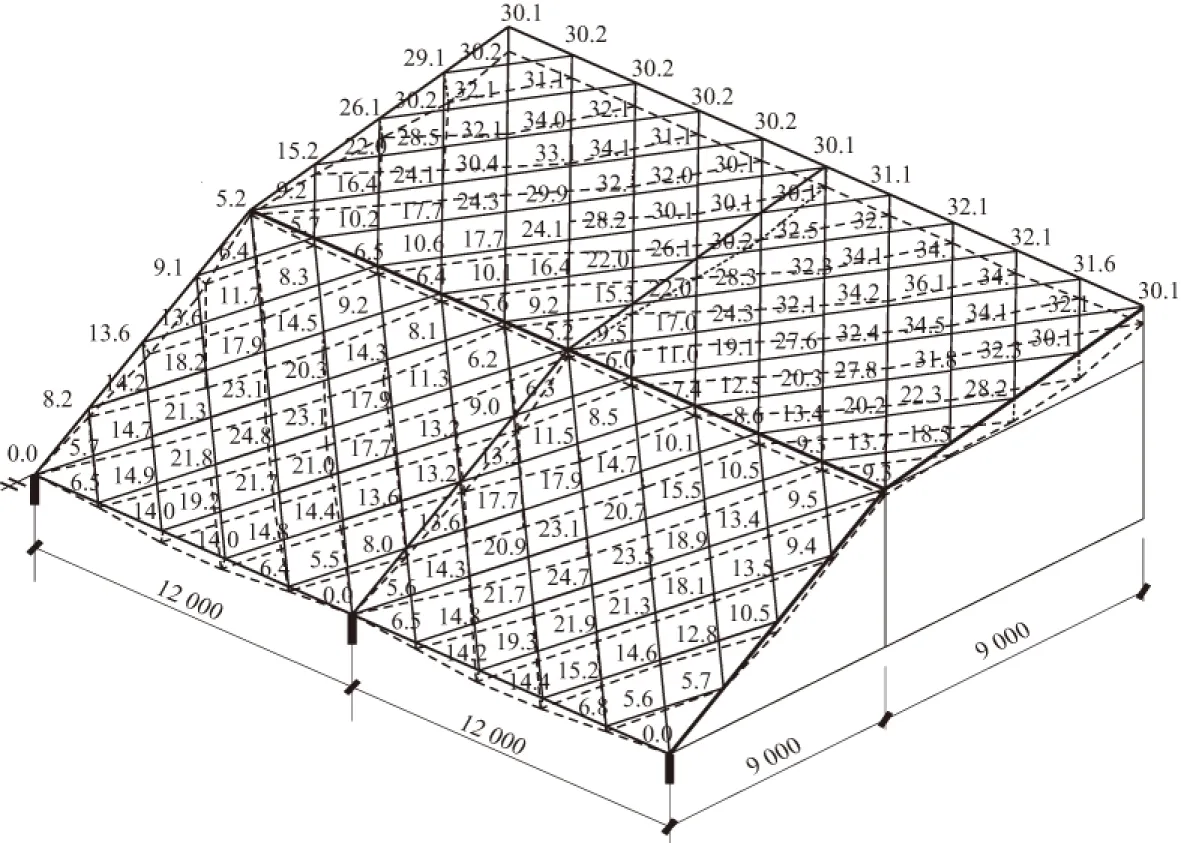
图4 屋盖肋梁挠度(单位：mm)

由于结构为双向对称结构，取1/4结构的挠度结果如图5所示，图4中挠度单位为mm。由图5可知，屋盖竖向挠度最大值为36.1 mm，出现在中脊线旁的屋面板位置，约为跨度的1/1 000，且密肋平板的挠度最大数值也为36.1 mm；脊线挠度较斜向肋小，可对斜向肋形成较强的约束效果。主拱梁线的挠度数值较平板变形小，对密肋平板形成了较好的支承。边梁的挠度数值较小，对密肋平板形成了较好的支承。

2.2.2 结构内力

由于屋盖呈双向对称，可将屋盖简化为1/4结构来分析，如图6、7所示，图中内力单位分别为kN和kN·m、尺寸单位均为mm。主拱与斜向密肋均为压弯构件，这两者在弯折处弯矩较大；边梁为弯曲构件，主要承受斜向密肋和传来的轴力与弯矩；脊线为受压杆件，且JX2的轴力略大于两侧脊线JX1。屋盖中主要受力构件为主拱和斜向肋；边梁为次要传力构件，主要承受斜向肋的轴力；脊线为斜向肋的约束构件，并承受斜向肋传递的轴力与弯矩，相比于正交正放网格时更有效地参与结构的整体受力。斜向肋与主拱支座相交处压力最大，说明斜向肋与主拱的协同工作效果良好，比正交正放网格时传力途径更加明确；而弯矩在折线处较大，并且斜向肋内力呈现远离主拱后数值逐级减弱的态势。在设计使需要根据变形情况考虑斜向肋与主拱相连处和折线处的配筋加强，且需要考虑受压构件的稳定性；主拱向肋在于支座和脊线相交处的弯矩较大，因此斜放网格拟柱面密肋折板网壳结构可以看作是由主拱、脊线、斜向肋、边梁组成的巨型梁系网格结构，且脊线对斜向肋的约束作用较强。

通过对屋盖进行的算例分析，发现屋盖的受力主要是沿着主拱，边梁，脊线梁以及主拱两侧的斜向密肋梁处传递，呈现出带状传力，将其分别称之为边梁平带、脊线平带以及主拱拱带，加之受力较小处的中间平带以及中间拱带共同构成了屋盖的传力路径，如图7所示。并在图7中，将屋盖结构中各个构件标号以便后期进行参数化分析。其中，主拱、脊线、斜向肋、边梁分别标注为ZG、JX、XL、BL。

图5 屋盖肋梁的轴力(单位：kN)

Fig.5 Axial force of rib beam of the roof (Unit:kN)

图6 屋盖肋梁的弯矩(单位：kN·m)

Fig.6 Moment of rib beam of the roof (Unit:kN·m)

图7 屋盖内力分区示意图(单位：mm)

3 屋盖静力性能的有限元参数化分析

3.1 矢跨比对屋盖静力特性的影响

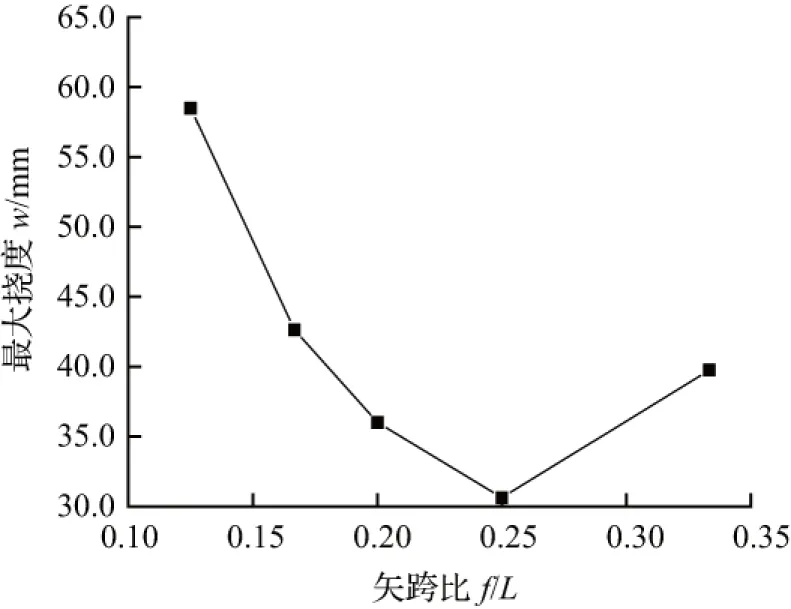
图8 矢跨比与屋盖挠度的关系

在原始算例基础上，仅改变屋盖矢跨比来计算。屋盖的挠度有限元分析结果如图8所示，对结构内力的影响如表1所示，其中F为轴力，M为弯矩。

考虑矢跨比不同对屋盖最大挠度的影响如图8所示，几个算例的最大值均位于中脊线两侧屋面板的第二个斜网格内，其数值为屋盖跨度的1/1175～1/616，满足规范的要求，表明屋盖的整体刚度良好。矢跨比从1/8增为1/3时，屋盖的挠度减小了32 %。矢跨比在小于1/6前减小的梯度较大，在1/6至1/4之间其减小的梯度减缓，而超过1/4后屋盖的最大挠度呈现上升的趋势，这是由于过大的矢跨比会增加屋盖结构的展开面积从而增加屋盖整体结构的自重，因此结构矢跨比宜取值为1/6～1/4。

从表1可知，结构的轴力F随着矢跨比的降低而增加，当矢跨比从1/8增大至1/3时，ZG1、JX2、BL1和XL1的1#区间轴力分别减小了45.9 %、50.3 %、50.4 %和38.9 %，且ZG1、JX2、XL1的8#区间轴力分别增大了43.3 %、55.2 %、108.3 %，BL1的3#区间轴力增幅为44.2 %；对于弯矩而言，屋盖矢跨比的不同对斜向肋和主拱支座处影响较小，但对BL1和JX2影响显著，例如矢跨比由1/8增至1/3时，BL1的3#区间、JX2的1#区间的弯矩增幅分别为29.8 %、59.8 %，而ZG1、XL1的1#区间弯矩最大变化率分别12.2 %、2.25 %，并且数值相对较小。

综上可得，低矢跨比时屋盖主要受力构件的内力均较大，此情况不利于大跨度屋盖受力；同时屋盖的矢跨比过高将削弱屋盖结构山墙框架处的面外刚度，以影响山墙框架对屋盖的约束作用。综合考虑矢跨比对屋盖的挠度的影响，结构矢跨比应控制在1/6～1/4为宜。

表1 矢跨比与构件内力的关系

3.2 斜向肋刚度对屋盖静力性能的影响

图9 斜向肋剖面高度对屋盖挠度的关系

为分析斜向肋梁的刚度变化对屋盖静力特性的影响，取斜肋梁截面高度分别为0.5、0.6、0.7、0.8、0.9 m计算5个算例。斜向肋截面的高度与屋盖跨度的斜肋高跨比约为1/72～1/40，结构最大挠度的随斜向肋刚度变化的计算结果如图9所示、对结构内力的影响如表2所示，其中F为轴力，M为弯矩。

出于构型原因，结构整体刚度主要受密肋平板的斜向肋刚度控制，因此降低肋的刚度将降低结构的整体刚度，如图9所示，当斜向肋截面高度取屋盖跨度的1/72即为0.5 m时，屋盖最大挠度为29.23 mm，将肋的截面高度增大为屋盖跨度的1/40即0.9 m时，屋盖最大挠度为28.1 mm，挠度减小约4 %。当斜肋高度取屋盖跨度的1/45时，即为0.8 m高时，屋盖挠度为27.981 mm，为图中挠度最小值，减小了4.5 %。

可见斜向肋截面高度的增加虽然可以提高屋盖的自身刚度，但由于斜向密肋梁高度的增大会增加屋盖的自重，这一点削弱了密肋梁对屋盖整体刚度的提升。因此对屋盖整体刚度与斜向肋刚度的联系较弱，可按屋盖拱向跨度的1/60～1/45确定斜向密肋的高度。

由表2可得，结构的轴力随着斜向肋刚度的降低而增加，当斜向肋的截面高度从0.5m增大为0.9m时，ZG1、JX2、BL1和XL1的1#节间轴力增幅分别为26.6 %、45.9 %、47.7 %和54.5 %，ZG1、JX2、XL1的8#节间轴力增幅分别为19.7 %、45.6 %、59.3 %，BL1的3#节间轴力增幅为36.4 %；对于弯矩，斜向肋改变对边梁的影响不大，但对主拱跨中处、斜向肋和脊线影响较大，例如斜向肋截面高度由0.5m增大至0.9m时，斜向肋1、脊线2的1#区间的弯矩增幅分别为78.9 %、59.8 %，ZG1、JX2中8#区间的弯矩降幅为55.7 %、71.3 %。而BL1的1#区间弯矩最大变化率仅5.5 %。对比柳勇斌[18]关于正交正放棱柱面密肋折板网壳中密肋对屋盖的静力性能分析，主要构件控制截面的弯矩增幅约为 23.6 %～38.7 %、轴力增幅约在39.1 %～50.0 %，且肋刚度的改变对屋盖的主拱内力影响较小，此时明显小于本文网格斜放时主要受力构件的内力增幅，反映出斜放网格的空间受力性能较正放网格时更好。

由此可得，斜向肋截面刚度的增大使得屋盖主拱、中脊线、边梁和斜向肋自身内力增长均较为明显。而斜向肋梁为结构中数量最多并与脊线和边梁为传力最密切的构件，可证明在棱柱面密肋网壳中，斜放网格比正放网格与主拱、边梁和脊线的传力效果更好，更具有空间结构效应。综合考虑斜向肋刚度对屋盖的挠度的影响，结构中斜向密肋横截面高度应控制屋盖结构跨度的1/60～1/45。

表2 结构内力与斜向密肋刚度的关系

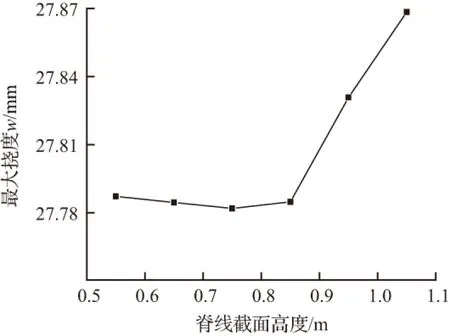
图 10脊线刚度与最大挠度的联系

3.3 脊线刚度对屋盖静力特性的影响

基于基本算例讨论脊线刚度的变化对屋盖挠度的影响，固定主拱截面高度为1.1m取主拱截面宽度为0.4 m。脊线的截面宽度均0.25 m，其截面高度分别为0.55、0.65、0.75、0.85、0.95、1.05 m，其余参数与基本算例一致，共计算了6个算例。脊线梁截面的高度与屋盖跨度的高跨比约为1/66～1/34。脊线刚度对屋盖挠度的影响如图10所示，对结构内力的影响如表3所示，其中F为轴力，M为弯矩。

如图10所示，改变脊线刚度后，挠度数值变化较小。脊线支承于主拱和端隔框架上，主要对斜向肋起支撑作用，本文算例取用的脊线截面高度约为跨度的1/72～1/33，脊线作为密肋平板的弹性支承，竖向荷载作用下将随密肋平板一起向下挠曲，因此脊线刚度对提高屋盖刚度收效甚微。

表3 脊线刚度对构件内力的关系

由表3可得，脊线刚度增大的同时结构轴力也会变大，当脊线的截面高度从0.55 m增大为1.05 m时，ZG1、JX2、BL1和XL1的1#区间轴力增幅分别为2 %、36.9 %、3.7 %和2.9 %，ZG1、JX2、XL1的8#区间轴力分别增加了为5 %、51.1 %、10 %，边梁1的3#区间轴力增幅为5.8 %，这说明脊线与斜向肋的传力效应比主拱明显；对于屋盖的弯矩，脊线刚度的改变除对自身的弯矩影响较大之外对其他的构件影响均非常小，例如脊线梁的横截面高度由0.55 m增大为1.05 m时，脊线2的1#节间的弯矩增幅为56.3 %，而8#节间的弯矩增加了76.8 %。并且BL1与ZG1的1#的节间弯矩最大变化率分别0.028 %和0.49 %，且数值大小相对较小。对比柳勇斌[18]关于正交正放棱柱面密肋折板网壳中脊线对屋盖的静力特性分析，脊线刚度的变化对拱向肋控制截面内力的影响较小，远低于本文的10 %。

图11 主拱刚度与最大挠度的关系

经分析得轴力由脊线传递至斜向肋的效果明显，证明通过将屋盖网格斜放使得脊线与斜向肋的受力联系比正放网格时更显著，达到了本文的预期研究目的。但脊线梁高度的增大会增加屋盖的自重这一点减弱了脊线梁高度增加对屋盖整体刚度增大的效果。综上，建议可按屋盖跨度的1/65～1/34为合适的脊线梁横截面高度。

3.4 主拱刚度对屋盖静力特性的影响

为分析主拱刚度对屋盖静力特性的影响，固定取主拱横截面宽度为0.40 m，仅改变结构中主拱的横截面高度分析6个案例，其剖面横向截面高度如下：0.60、0.70、0.80、0.90、1.0、1.1 m。其对挠度影响的有限元计算结果如图11所示，对结构内力的影响如表4所示，其中F为轴力、M为弯矩。

结构最大挠度发生在斜向密肋平板上，从图7所示的内力分区示意图可知，竖向荷载主要沿主拱拱带传递，因此结构最大挠度随主拱刚度的提高而降低，计算结果如图11所示。当主拱截面高度取屋盖跨度的1/72时，结构最大挠度为36.02 mm；而主拱截面高度取屋盖跨度的1/33时，最大挠度为27.79 mm，挠度降低了29.6 %，因此提高主拱刚度对增强屋盖的整体刚度有所帮助。

表4 主拱刚度对结构内力的影响

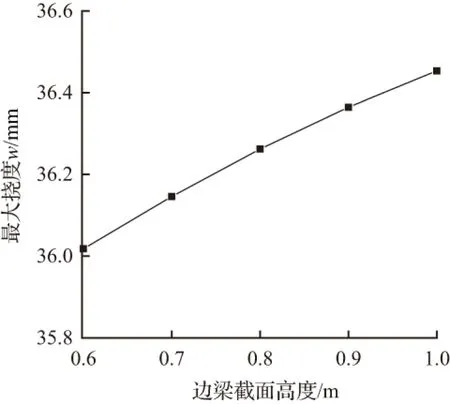
图12 边梁刚度与屋盖挠度关系

表4给出了屋盖部分构件内力随主拱高度变化的情况。当主拱截面高度从0.6 m增大至1.1 m时，ZG1与BL1的1#区间轴力增幅分别为18.9 %和33.1 %，JX2和XL1的1#区间轴力降低幅度分别为33.2 %、22.4 %。ZG1的8#区间中轴力增幅23 %、XL1的8#区间轴力降低了15.7 %，JX2的8#区间轴力降幅为13.9 %，BL1的3#区间轴力降幅为10.2 %；对于弯矩，主拱刚度的改变除对自身弯矩影响较大之外对其他构件影响较小，例如主拱梁的横截面高度由0.6 m增大至1.1m时，主拱梁1#区间的弯矩增幅为40.3 %，主ZG1的8#区间的弯矩增加了65.9 %。而JX2中1#区间弯矩最大变化率分别29.9 %。BL1、XL1中1#区间弯矩分别降低3.3 %和27.3 %。

主拱梁刚度增大会使屋盖中的主要传力构件斜向肋的内力有所下降，因此增大主拱刚度对增大结构刚度及降低结构用钢量是有利的，并且主拱刚度增大对相连的斜向肋弯矩减小有较大帮助，体现了主拱对斜向肋的良好约束效果，结合主拱刚度对屋盖挠度的变化特性，推荐主拱的截面高度可按屋盖跨度的1/51～1/36确定。

3.5 边梁刚度对屋盖静力特性的关系

结构在点支承时边梁是重要传力构件，且以受弯为主，这里取边梁的截面宽度为0.4 m，仅改变边梁的截面高度hL计算5个算例，且hL按级差0.1 m由0.6 m增大至1.0 m，以考察边梁刚度的变化对屋盖挠度影响，其有限元分析结果如图12所示。对结构内力的影响如表5所示，其中F为轴力，M为弯矩。

出于构型原因，结构整体刚度主要受密肋平板的斜向肋和主拱刚度控制，而斜向肋支撑在边梁上，因此降低边梁的刚度将降低结构的整体刚度，如图12所示，当边梁截面高度取屋盖跨度的1/60时即0.6 m时，最大挠度为36.02 mm，将边梁的截面高度增大为屋盖跨度的1/36即1 m时，屋盖最大挠度为36.46 mm，挠度增大约1.2 %。因此边梁高度的增大对结构刚度的提升效果不大。

究其原因，主要是边梁作为主拱肋梁的约束时承受主拱传来的弯矩使得边梁截面受扭，而矩形边梁在抗扭时发生转动主要控制因素是截面宽度，并且考虑边梁自重将影响结构的内力变化，因此取边梁跨度的1/20～1/15为边梁的截面高度。

如表5可得，当边梁刚度的增大时，结构除边梁自身外各构件的轴力均降低，当边梁的截面高度从0.6 m增大为1 m时，边梁内力增加，且弯矩增幅远大于轴力。并且边梁刚度对脊线弯矩及斜向肋弯矩影响显著，如JX2的1#、8#节间弯矩分别变化了59.8 %、71.3 %，XL1的1#节间弯减小28.7 %。且边梁对ZG1的内力影响较小，当边梁截面高度增大，ZG1中1#节间的轴力降幅仅为0.8 %，而弯矩降幅为2.5 %。

表5 边梁刚度对构件受力的关系

图13 屋面板厚度与结构挠度的关系

综上所述，边梁刚度在屋盖刚度中占比不大，脊线、斜向密肋刚度与边梁刚度关联较大，这是边梁约束斜向肋后进一步约束脊线的缘故，从侧面反映了结构的传力途径明确的特点。考虑边梁自重增大的综合影响，取边梁高度为边梁跨度的1/20～1/15。

3.6 屋面板厚度对屋盖静力特性的影响

在基本分析算例的基础上仅改变屋面板厚来计算4个算例，板厚分别为60、80、100、120 mm。以此来讨论屋面板厚度的变化对屋盖最大挠度的影响。其分析结果下图13所示，对结构内力的影响如表6所示，其中F为轴力，M为弯矩。

计算结果表明，屋盖的最大挠度随屋面板厚度的增加而降低，如图13所示，当屋面板厚为60 mm时，最大挠度为36.02 mm；当板厚为120 mm，最大挠度为30.69 mm，挠度降低约14.8 %，因此增加屋面板厚度有利于结构整体刚度的控制。

可见屋面板厚度的增加可以略微提高屋盖的自身刚度。在混凝土结构设计规范中，规定了屋面板最小厚度来保证屋盖结构的安全、可靠性。工程设计中，结构屋面板厚度增大会增大结构的自重，而结构的自重与地震效应成正相关，这会对结构的抗震带来不利影响。在满足结构正常使用承载力的要求下，屋面板厚度不宜过大以致增加结构的自重，建议屋面板在满足使用条件的情况下一般取80或100 mm即可。

表6 屋面板刚度与结构受力的关系

从表6可知，屋面板厚度的增大时主拱和斜向肋的轴力减小，当屋面板的截面厚度从60 mm增大为120 mm时，ZG1、BL1和XL1中1#节间轴力分别减小了23.4 %、6.9 %和19.03 %，ZG1的8#节间轴力也降低了28.1 %，但对边梁轴力影响不大。对于弯矩，屋面板厚度的改变对BL1的影响不大，但对ZG1和XL1截面处影响较大。当斜向肋的截面高度由60 mm增大为120mm时，ZG1和XL1的1#节间弯矩分别减少9.8 %、13.2 %，BL1的3#节间的弯矩降幅仅为3.5 %。

综上所述，屋面板厚度增加对减小结构最大挠度，提高结构整体刚度具有显著的作用，主拱、斜向密肋梁的内力会随着屋面板厚度的增大而有一定程度的降低，但对边梁的内力影响不明显。在满足结构正常使用承载力的要求下，屋面板厚度不宜过大以致增加结构的自重，建议屋面板在满足使用条件的情况下一般取80 mm或100 mm即可。

4 结论

① 斜网格拟柱面密肋折板网壳结构可看作由各折线梁构件组成的巨型空间网格结构，空间受力性能佳，且主拱和斜向密肋是屋盖中的主要受力构件；主拱和斜向肋可视为偏心压弯构件，并对其折角处的配筋采用加强处理。

② 矢跨比对屋盖结构挠度的影响较大，同时较大的矢跨比会减弱山墙框架的面外刚度，使山墙框架对屋盖的约束作用减弱进而影响结构总体刚度，建议屋盖的矢跨比取1/6～1/4。

③ 斜向肋梁是整个屋盖结构中主要的传力构件之一，提高斜向肋梁的横截面刚度有利于提高屋盖整体刚度，建议斜向密肋梁的横截面高度按屋盖拱向跨度的1/60～1/45确定。

④ 斜放网格时脊线梁与斜向肋之间的传力效果比正放网格明显，建议脊线梁的横截面高度按屋盖跨度的1/65～1/34来确定；主拱刚度在屋盖整体刚度贡献较大，建议主拱梁的横截面高度可取屋盖跨度的1/51～1/36。

⑤ 结构的内力随边梁高度的增加近似呈线性增大，但增幅不大，取边梁跨度的1/20～1/15为边梁横截面高度；屋面板作为结构的刚度储备在满足混凝土设计规范的标准下不应取值过大，以致增加屋盖的自重。建议屋面板厚在满足使用条件后不宜取值太大。