基于密集城市街道的车载衰落信道模型研究
陈珍,周杰,岳壮
(南京信息工程大学 电子与信息工程学院,江苏 南京 210044)
0 引言
开发现实的模型可以准确高效的描述传播信道,从而获得高质量的服务,因此无线传播的几何模型引起了人们广泛的关注[1-3]。基于几何的信道模型,例如单环模型[4-5],双环模型[6-7]和椭圆模型[8]构成了一个重要的信道模型类别。为了开发更稳定有效的车辆对车辆(vehicle-to-vehicle,V2V)通信系统,需要准确了解衰落信道特性。由于V2V移动无线电信道的统计特性与当今蜂窝移动通信系统中的传播特性显著不同,因此需要用于V2V通信的新信道模型。预计V2V通信系统将在包括智能交通系统,移动自组织网络和基于中继的蜂窝网络等各种领域中发挥重要作用。因此,对于未来V2V通信系统的开发,对基础衰落信道特性及其统计特性的扎实了解非常重要。在这种情况下,文献[9]提出了一种基于几何街道散射模型的窄带单输入单输出(single-input single-output,SISO)车载信道模型,利用大量具有不同散射体分布的基本信道模型,例如均匀分布,高斯分布,拉普拉斯分布和冯·米塞斯分布,用于描述发射角(angle-of-departure,AOD)和到达角(angle-of-arrival,AOA)的统计特征。文献[10]针对标准街道传输环境提出了一种新型的统计信道模型,该模型的散射体以散射条纹形式均匀分布在街道两侧,从无线电信道的角度来看,与传统移动通信的根本区别在于发射机和接收机都在移动。文献[11-12]在几何双环模型的基础上进行扩展提出了移动到移动(mobile-to-mobile,M2M)通信系统的随机多输入多输出(multiple-input multiple-output,MIMO)V2V参考信道模型,在各向同性和单反射散射的情况下研究模型的统计特性。文献[13]提出了一种用于街角传播场景的MIMO车载通信信道模型,发射机和接收机仅配备两个全向天线,利用双瑞利分布模拟V2V通信场景中的多径衰落。尽管这些模型对于M2M通信的性能分析是有用的,但它们并不总是覆盖所有不同的重要散射环境,并且不能应用于每个街道,尤其是频繁发生车祸的十字路口,这就证明了建立这种场景下信道模型的必要性。
文献[14-15]已经开发了一个几何信道模型来描述十字路口场景下信号传输特性,然而这类信道模型的适用范围比较局限,主要研究了分布在发射机和接收机周围一定数量的散射体,并且对信道模型的统计特性研究甚少。然而,大多数情况下城市环境中的散射体数量都是无限的,因此它们不能准确描述街道V2V散射信道的传输环境。与已有的十字路口环境模型[14-15]相比,本文主要考虑了当散射体数量趋于无穷大时,衰落信道的时间、频率和空间相关性质,同时通过在发射端和接收端配置的矩形天线阵列来分析车辆行驶时的通信系统性能。
针对特殊的十字路口街道散射环境,本研究提出了一种改进型散射信道模型。基于使用T型模型的建模概念,并将其扩展为十字路口模型。该模型能够准确描述标准街道和十字路口等移动通信环境的重要信道特征参数,并能够将其应用于多输入多输出通信系统性能的仿真中。假设散射体各向同性的情况下,利用发射角和到达角的关系推导出参考模型的相关函数。然后根据推导的时间自相关和频率相关函数结果和仿真模型进行对比,表明参考模型和仿真模型吻合,证明了该信道模型的准确性。同时为了证实本模型的可行性,将参考模型的仿真结果与文献[16-17]进行对比,表明仿真信道模型的统计特性符合理论与经验,拓展了室外V2V无线通信系统的分析与应用。
1 城市街道散射信道模型
本文提出的V2V无线通信信道模型的典型传输环境如图1所示,假设视线(line-of-sight,LOS)和非视距(non-line-of-sight,NLOS)传播,并且在模型中考虑单次和二次散射路径。道路两侧的树木和建筑物为散射体,TX为发射机,RX为接收机。衰落信道的统计特性主要取决于发射机和接收机周围的散射体分布,因此建立准确的信道模型是十分重要的。
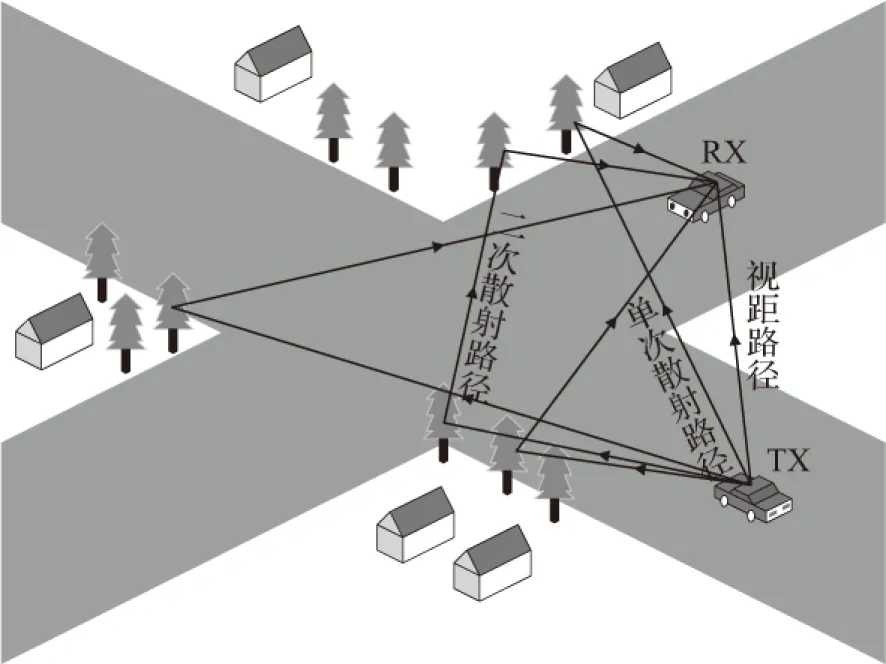
图1 V2V移动无线传输环境
为了令提出的模型适用于城市街道十字路口环境,利用以下假设条件来更好地设计模型,以便能够理论导出V2V信道模型(图2)参数。
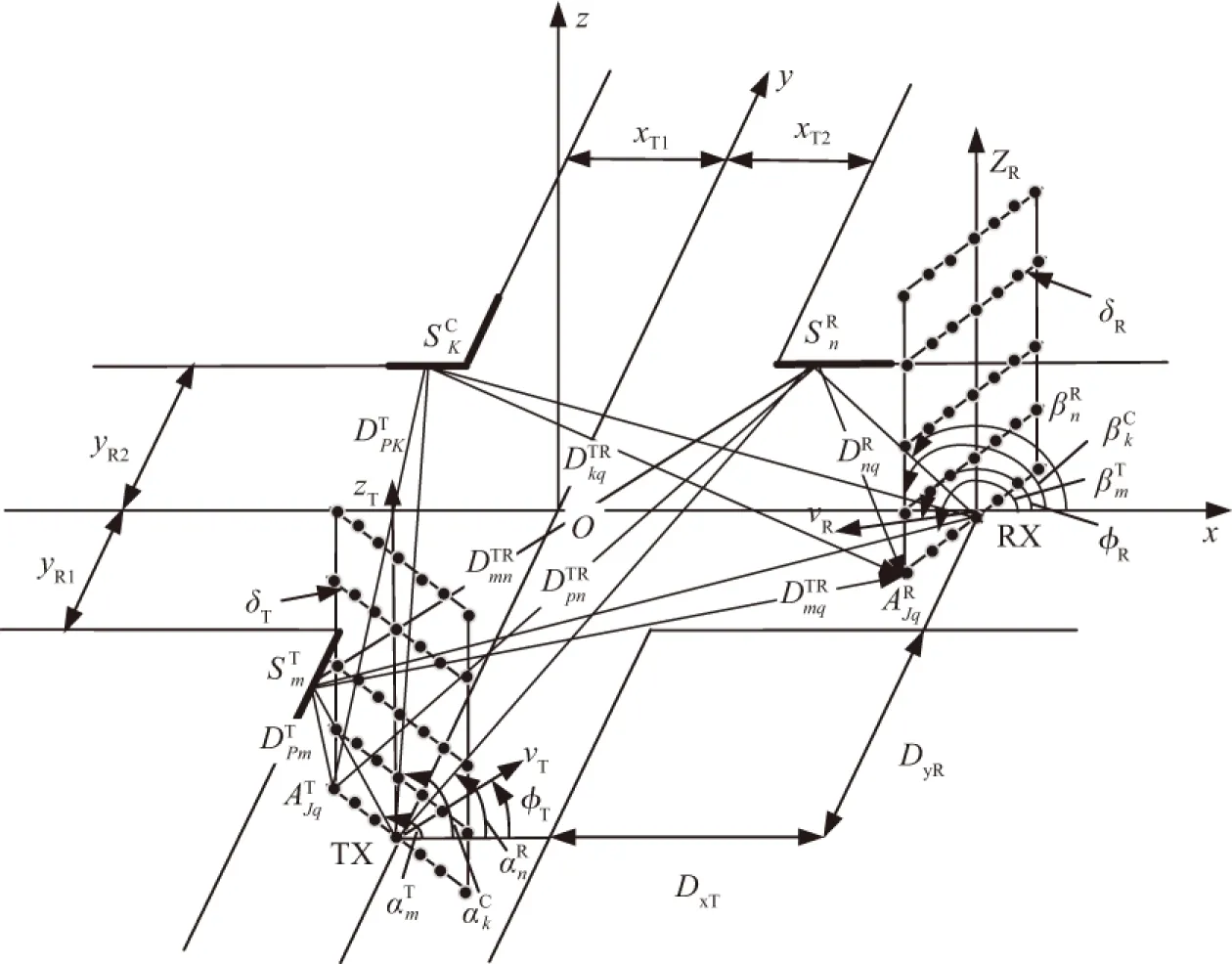
图2 十字路口散射信道模型
① 图2中的散射体均匀分布在街道两侧,不考虑散射区域以外的散射体的影响,仅考虑视距路径、单次散射路径和二次散射路径;
② 假设图2中的每个散射体都是全向辐射元件,具有相同的反射系数,且不产生路径损耗;
③ 在图2所示的十字路口场景散射区域内,每个散射体都以恒等于1的概率产生一条电波发射信号,电磁信号从发射端经过视距路径和非视距路径到达接收端。
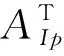
2 密集街道V2V信道模型
2.1 MIMO信道模型
MIMO系统采用多个发射天线和多个接收天线,与SISO通信系统相比,不仅可以提高系统性能,而且还可以提高容量。这一事实,再加上可以在大型车辆表面放置多单元天线已经成为可能,使得MIMO技术对于V2V通信非常有吸引力。根据以前的研究[13-14],当天线数量很大时,平面波前假设不适合大规模MIMO信道,因为天线阵列的特性不容忽视。因此,本文在所提出的通道模型中应用具有球面波前的均匀矩形阵列,使用非频率选择性瑞利衰落信道模型分析天线阵列性能。信道脉冲响应表示为:
(1)
其中,J是发射端天线总数量,aj(t)是发射端第j个天线复振幅,α(φj,θj)是均匀矩阵接收信号矢量,且0≤φj<2π,0≤θj<π。如图3所示,φj和θj是接收端第j个天线的水平方位到达角和俯仰角。图3坐标系中xoy平面上设定一个I×MR的均匀矩形天线阵列,从图3中可以看出,空间三维天线阵列的接收模型是二维模型在高度上的拓展,接收信号矢量可以表示为:

([1,ejμ,…,ej(I-1)μ]T[1,ejv,…,ej(MR-1)v]),
(2)
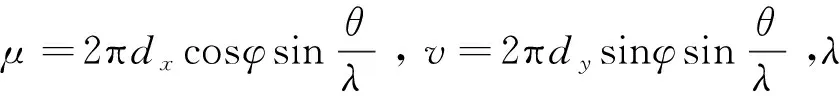
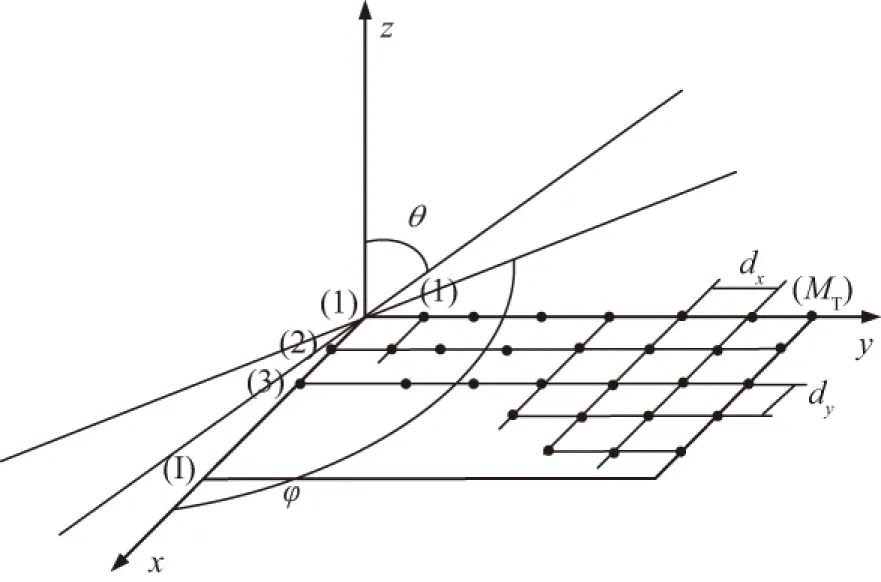
图3 接收端处的均匀矩阵阵列模型
2.2 波达信号AOA和AOD
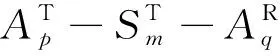
(3)
(4)
其中:
(5)
(6)
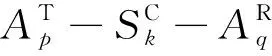
(7)
其中,lc表示拐角区域的范围。
(8)
(9)
2.3 几何散射信道模型
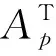
(10)
其视距散射分量可以分别表示为:
(11)
式中,λ表示波长,传播延迟τLOS′=DLOS/c0,其中c0表示光速,DLOS表示发射机到接收机的距离。
单反射发射端散射分量可以表示为:
(12)
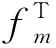
(13)
(14)
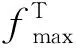
(15)
(16)
单反射接收端散射分量可以表示为:
(17)
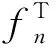
(18)
(19)
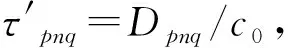
(20)
(21)
拐角单反射散射分量可以表示为:
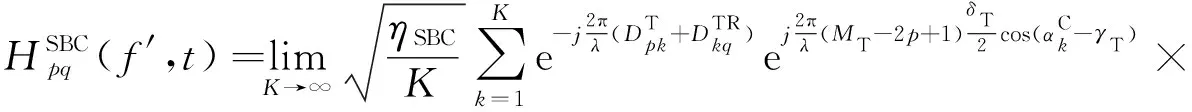
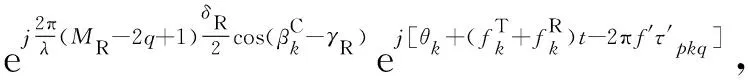
(22)
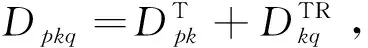
(23)
(24)
双反射散射分量可以表示为:
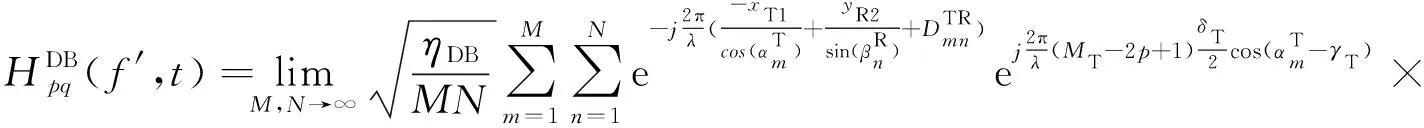
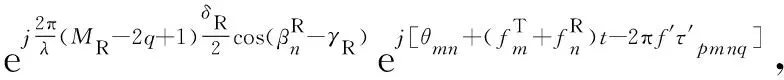
(25)
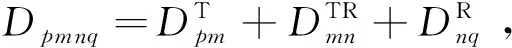
(26)
式中,参数ηLOS、ηSBT、ηSBR、ηSBC和ηDB表示各个散射分量的平均功率,相位θm、θn、θk和θmn在[0,2π]内均匀分布。
3 相关函数分析
为了更好地了解V2V无线通信系统,以应用于ad-hoc网络和智能交通系统,需要考虑模型时域、频域和空域的信道相关特性,空—时—频互相关函数可以定义为:
(27)
其中,E{·}表示期望算子,再利用式(10)可得到空—时—频互相关函数的表达式为:
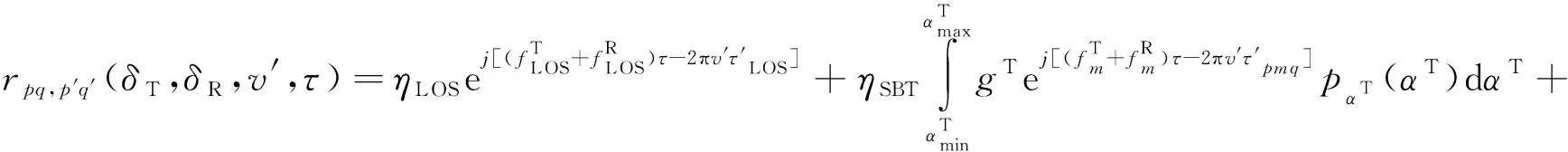
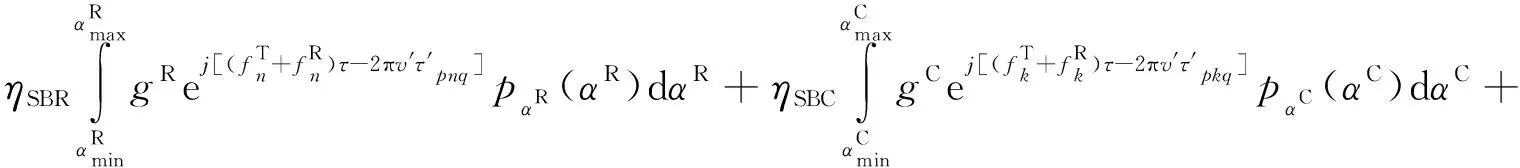
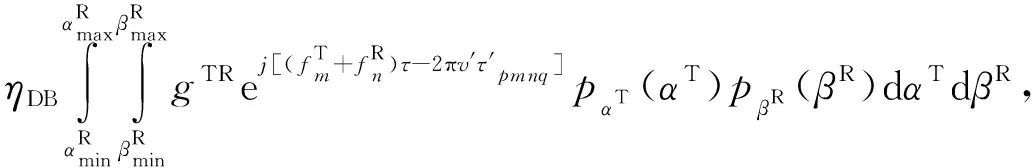
(28)
其中:
(29)
(30)
(31)
(32)
模型的空间特征可以通过空间相关函数来描述,定义为:
(33)
对比式(30)发现当v′=0、τ=0可以得到空间互相关函数,即rpq,p′q′(δT,δR)=rpq,p′q′(δT,δR,0,0)。当d=δT=δR时,可以根据式(31)得到V2V信道模型的空间相关系数。
相似地,模型的时频特性可以通过时频互相关函数来描述,定义为:
(34)
对比式(30)发现当δT=δR=0可以得到时频互相关函数,即rpq,p′q′(v′,τ)=rpq,p′q′(0,0,v′,τ)。
所提出街道模型的时间特性可以通过时间自相关函数来描述,定义为:
(35)
令δT=δR=0以及v′=0可以得到信道的时间自相关函数rpq(τ)=rpq,p′q′(0,0,0,τ)。
模型的频率特性可以通过频率相关函数来描述,定义为:
(36)
令δT=δR=0以及τ=0可以得到信道的时间自相关函数rτ′(v′)=rpq,p′q′(0,0,v′,0)。
4 数值与仿真结果
通过对模型进行仿真来评估V2V通信系统,为了不失一般性,散射区域长度满足xT1=yR1=15 m,xT2=yR2=5 m,lc=5 m。发射端天线阵列的倾斜角为γT=0°,接收端天线阵列的倾斜角为γR=90°,发射机运动夹角为φT=90°,接收机运动夹角为φR=180°,运动速度为vT=vR=10 m/s,载波频率为fc=5.9 GHz。
图4直观地描述了发射端和接收端的天线间距对空间互相关函数的影响。从图4中可知,当天线阵列间距δT和δR为零时,空间互相关函数得到最大值,随着天线阵列间距的增大呈缓慢衰落趋势直至发射机和接收机的天线阵列间距与波长λ的倍数为5时得到其最小值。此实验结果可应用于现实的街道场景,通过增大天线阵列的间距来减小其相关性。
图5为时间和频率对时频互相关函数的影响分布图。平面波从第p根发射天线到达从第q根接收天线的LOS传输过程和经过散射体的NLOS过程中,当时间延迟和频率为0时,互相关函数达到最大值1,随着时间延迟和频率的增加,互相关函数迅速减小,并小幅度震荡衰落,最终减小到一定值。此仿真结果与Avazov的街道模型[18]的仿真结果相吻合,证实了此模型可用来描述交叉路口V2V通信场景的可行性。
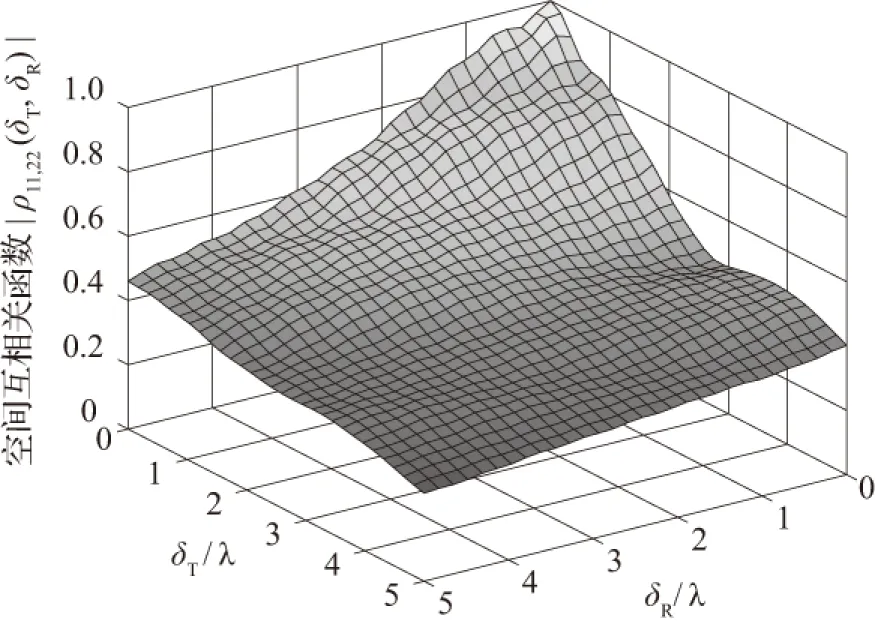
图4 空间互相关函数
Fig.4 Space cross-correlation function
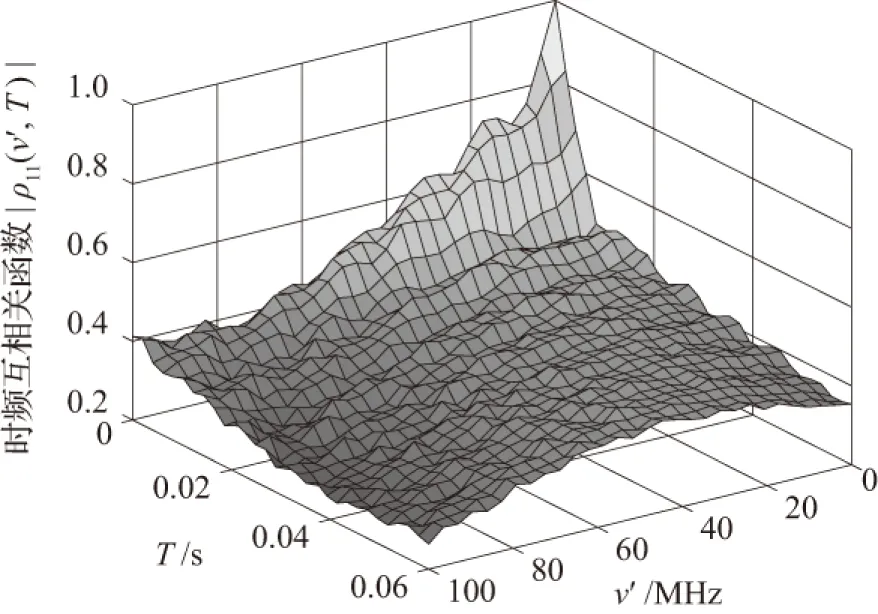
图5 时频互相关函数
Fig.5 Time-frequency cross-correlation function
图6为发射机和接收机之间的距离对时间自相关函数的影响分布图。由图6可知,在最开始的0.005 s的时间延迟内,时间自相关函数迅速衰减,这是由于发射机和接收机的开始运动导致散射体和反射次数的增加导致的。当发射机和接收机之间的距离增加时,平面波从发射端经过散射体到达接收端的路径长度增加,导致时间自相关函数减小,这符合理论与实践。对比文献[16]的城市矩形街道模型和Chelli[17]的T型路口模型,该模型的时间自相关性更低,更加适用于特定室外环境的V2V通信。
图7为发射机和接收机之间的距离对频率相关函数的影响分布图。从图7中可以看出,在不同的参数条件下参考模型和仿真模型的曲线基本一致。此外,发射机和接收机接近交叉路口时,频率相关函数减小,而且当距离变化时,频率相关函数只有略微的改变。通常,频率相关函数对于参数的变化不是非常敏感。同时频率相关函数随着频率的增加而减小,这与Avazov[16]等构建的城市街道V2V信道模型的频率相关函数走势类似,进一步说明了所提出的模型描述车辆道路通信系统的合理性和可行性。
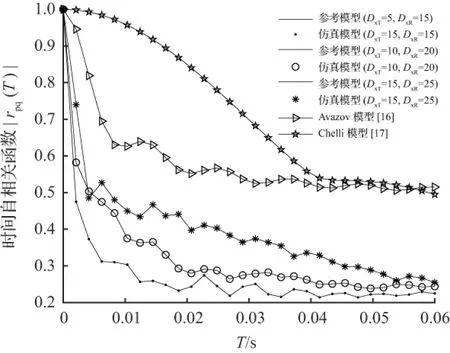
图6 不同距离条件下的时间自相关函数
Fig.6 Temporal autocorrelation function under different distance conditions
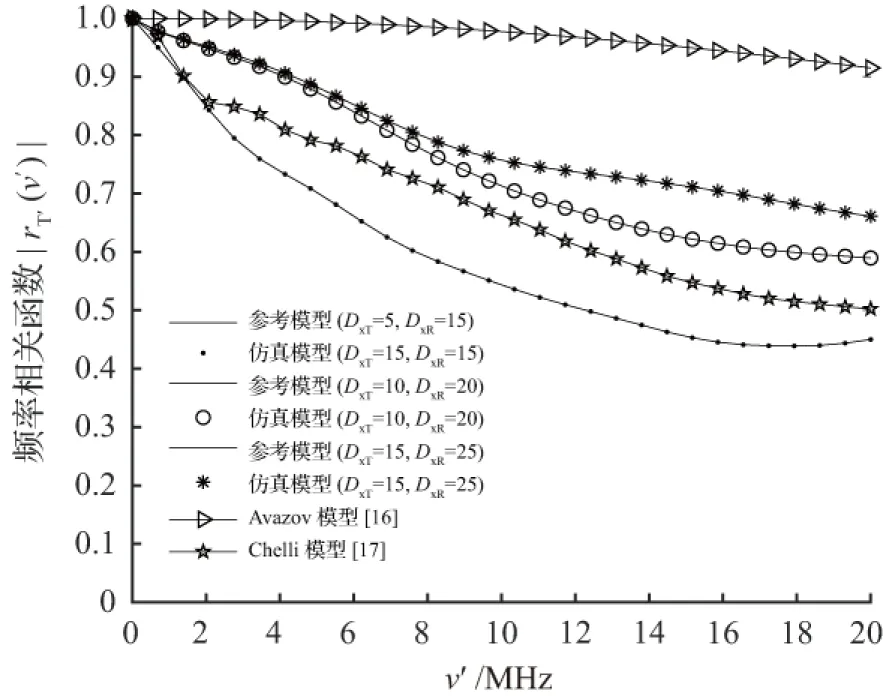
图7 不同距离条件下的频率相关函数
Fig.7 Frequency correlation function under different distance conditions
图8为发射机和接收机之间的距离以及天线间距对空间相关系数的影响分布图。当发射机和接收机同时向交叉路口行驶时,两者之间的距离较小,空间相关系数在天线间距为1时呈上下震荡趋势,最终在空间相关系数为0.4波动,这一趋势与文献[16]的矩形街道场景下的空间相关系数相符。当发射机和接收机远离交叉路口行驶时,距离增大,空间相关系数随着天线间距的增大而迅速减小,这与文献[17]T型路口的研究一致,都可通过增加发射机和接收机所配置的天线阵列距离来减小相关性,以增大信道容量来提高无线通信系统的性能。
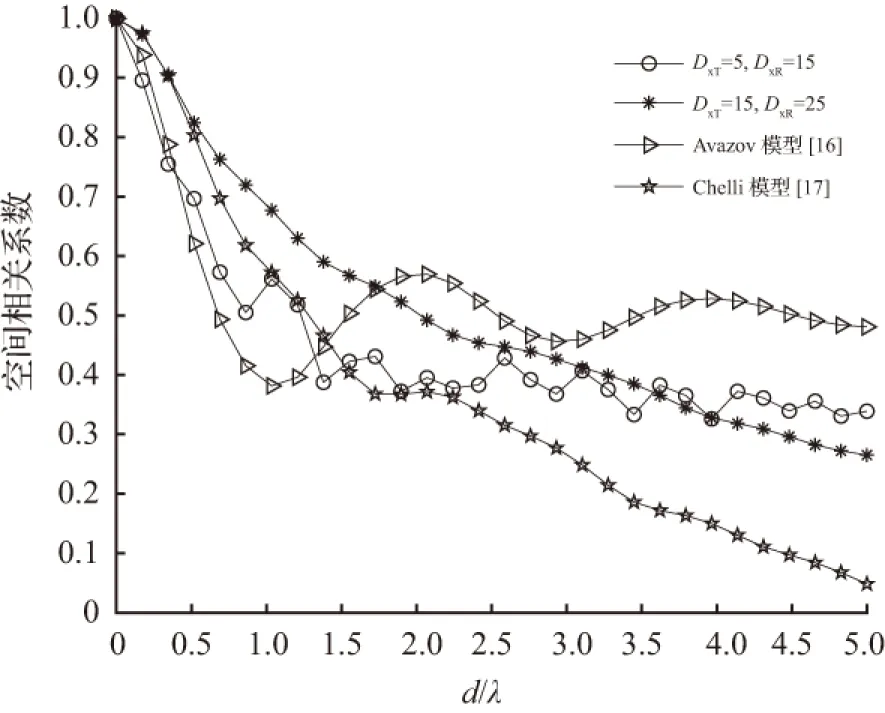
图8 不同距离条件下的空间相关系数
5 结论
本文以典型的T型交叉路口为基础,提出了一种新型十字路口场景下的MIMO车载通信信道模型。考虑到视距和非视距的传播条件,推导了参考模型的空间互相关函数、时频互相关函数、时间自相关函数以及频率相关函数的解析表达式,研究了所提出的信道模型的统计特性,仿真并分析了天线阵列之间的间距、时间、频率、发射机和接收机之间的距离等对其统计特征的影响。与以往车载信道模型对比表明,本模型适用于城市道路中的十字交叉路口,为评估特定传播条件下V2V通信系统的性能提供了重要框架。

