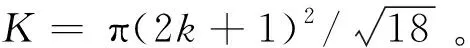三维异质无线网络中的最小虚拟骨干网

易梦,梁家荣*,覃斌

(1.广西大学 计算机与电子信息学院, 广西 南宁 530004;2.广西多媒体通信与网络技术重点实验室，广西 南宁 530004)

0 引言

在传统的有线网络中，信号通过有限的物理电缆从一个设备传递到另一个设备，数据传输发生在露天和给定覆盖区域内，容易受到气候、地理环境等各方面影响。而无线网络不需要固定的基础建站设施，与传统的有线网络和移动细胞网络不同，无线网络的监控区域通常不方便拥有集中控制和路由的基础设施，例如无线接入点或基站。无线传感器网络 (wireless sensor network，WSN)是一种由大量可以感知外部世界的传感器组成的分布式传感网络。目前，无线网络已广泛应用于环境监测、健康应用、灾难救援、战场监控、音乐会、交通控制、移动计算、军事行动等难以在网络中安装基站或物理主干的应用领域[1-4]。与传统的无线网络相比，WSN具有容量大、自组织、多跳通信等优点。WSN中的任意一对传感器都可以通过直接链路或多跳相邻节点转发信息来实现通信。然而，即使是目前应用最广泛的洪泛广播技术也存在着严重的问题，如广播风暴、冗余信息转发、节点间信道争用、转发信号冲突等，导致网络资源利用率下降。为了有效地解决网络拓扑的变异性，减少冗余路由所带来的不必要的能源消耗，避免信息冲突和广播风暴，EPHREMIDE等[5]注意到以往的无线网络路由算法都没有尝试使用与分组蜂窝网络的物理主干基础设施类似的结构，于是在1987年引入了虚拟骨干网(virtual backbone，VB)的概念。虚拟骨干网是无线网络节点的一个子集，网络中任意节点之间的操作请求都可以转化为虚拟骨干网上的同源操作。在虚拟骨干网中，每个普通节点只需要将消息发送到其位于虚拟骨干网中的节点即可，虚拟主干中的节点将作为中继节点帮助它将这些消息转发到它的目的节点。因此，虚拟骨干网可以大大减少转发进程，一旦网络中使用了虚拟骨干网，路由路径搜索空间将被限制在骨干网中，而不是整个网络，这可以导致更短的路由路径搜索时间、更小的路由表大小以及更简单的路由维护。在无线传感器网络中，构建虚拟骨干网的方法有很多种，其中基于连通控制集(connected dominant set, CDS)的虚拟骨干网的构建是现有的无线传感器网络虚拟骨干网构建方法中的一种常用的方法。最小连通控制集(minimum connected dominant set, MCDS)同时意味着性能更好的最小虚拟骨干(minimum virtual backbone, MVB)，因此笔者可以通过在图中构造一个MCDS来解决在网络中寻求MVB的问题。

在均质无线网络中，现有的许多研究[6-8]都是利用单位圆盘图(unit disk graph ，UDG)对二维欧几米德平面上的网络进行建模，用单位圆盘图上的节点来代替一个个路由器，节点的传输半径则代表路由器的传输半径。然而，当笔者在研究山区[9]、海洋环境监测、海洋采样网络[10]等三维空间领域时，UDG模型并不适用。因此本文使用单位球图(unit ball graph ，UBG)对三维无线网络进行建模。事实上，UDG可以看作是UBG的一个特例，即所有节点都被约束在同一个平面上，但是UBG的几何性质比UDG更复杂，因此对UBG的最小连通控制集(MCDS)进行近似分析要困难得多。注意到，在UDG和UBG中，节点的传输半径都相同。最小连通控制集问题已经被证明是NP-难问题，因此很多文献提出通过来寻找一个MCDS的近似算法来解决这个问题。通常来说，这些近似算法一般分为两个阶段，首先在第一阶段，构造一个极大独立集(MIS)，这个极大独立集同时也是一个控制集；然后在第二阶段通过添加一些其他的点作为连接点将控制集里面的点连通起来，构成一个连通控制集。为了分析CDS的近似比，本文需要分解算法，并将每个部分分别与最优解进行比较。所以极大独立集与最优解的比值在求解这个问题中有着至关重要的作用。本文令M表示一个极大独立集，opt表示MCDS的大小，在UDG中[11]，证明了|M|≤3.8opt+1.2 ，经过一系列算法以及几何方法的改进,目前已有文献中最好的结果是 |M|≤3opt+3[12]。在UBG中，KIM等[13]证明了|M|≤10.917opt+1.083以及算法的近似比为14.937，这是目前已知最优的极大独立集的上界和CDS的算法近似比。GAO等[14]指出文献[13]的分析过程中有一个错误，并进行了修正。优化CDS算法近似比的另一个方向是减少连接点的个数，在UDG中通常采用最小斯坦纳树的方法。

相比与均质无线网络，异质无线网络的研究难度更大，相关文献相对较少。在异质无线网络中，所有节点的传输半径不一定相等，因此在信息传输过程中将出现单向链路，通常用有向图来对网络拓扑结构进行建模。在二维欧几米德平面上，通常用圆盘图(disk graph，DG)表示一个有向图，图上的每个节点代表一个传感器，以节点为中心的圆盘代表传感器的传输范围，每个节点都有自己的传输半径。注意只有当两个传感器都在彼此的传输范围内，才认为它们可以正常通信，所以在具有双向链路圆盘图(disk graphs with bidirectional links，DGB)中，图中的所有边都是双向的[15]。针对三维空间领域如水下传感器网络、海洋采样网络等实际问题，三维异质无线传感器网络更具有一定的现实意义，在本文中，将之抽象为双向链路球图(ball graphs with bidirectional links ，BGB)。

在另一方面，目前基于CDS的算法设计的大部分研究中，仅仅考虑了CDS的大小，针对基于能量选择的CDS构造算法的文献并不多见。实际上，由于数据传输速率、CPU容量、内存空间等资源的限制，网络拓扑结构也容易受到硬件损坏、能耗、传感器移动、网络入侵等因素的影响，特别是节点能量直接影响网络的寿命。随着微处理器和电子技术的迅速发展，传感器节点的通信半径可以相应地改变，节点可以根据实际应用情况调整传输功率，从而降低网络能耗，延长网络寿命。LI等[16]介绍了调节传输半径的集中式算法。该算法虽然可以取得较好的效果，但需要更频繁的信息交换、更大的存储空间和更高的能量损耗，不利于网络拓扑结构的变化。在文献[17]中，JIANGBAO等提出了一种分布式CDS构建算法，称为Power Selection算法(PSA)，该算法在构建CDS时可以根据网络的具体情况自动选择合适的传输功率，但未考虑三维空间上的情况。受此启发，本文在三维异质无线传感器网络抽象出的BGB模型下，提出了一个基于能量选择的MCDS构造算法ESA(energy selection algorithm，ESA)。

1 预备知识

异质无线传感器网络由许多具有无线通信功能的传感器节点组成。为了便于研究，本文假设它们随机分布在固定的自由空间中，并且没有障碍物阻碍通信。给定一个有向球图G=(V,E)，V表示图G中的点集，E表示图G的边集。对任意节点vi∈V，都有一个传输半径ri∈[rmin,rmax]，rmin,rmax分别表示网络中节点的最小传输半径和最大传输半径，k=rmax/rmin表示最大传输半径和最小传输半径之比。对于V中的任意两点u和v，ru,rv分别表示其传输半径，当且仅当u和v之间的欧氏距离d(u,v)≤ru时，存在单向边(u,v)∈E，此时称v是u的控制邻点，u同时也是v的吸收邻点，u能够向v发送消息。如果u和v之间的欧氏距离d(u,v)≤min{ru,rv}，则称u和v之间具有双向边，(u,v)∈E且(v,u)∈E，它们可以互相发送消息，互为邻点。在本文中，只研究具有双向链路的有向球图。

节点u的控制邻点集表示为N+(u)={v|(u,v)∈E,v∈V}，N+[u]=N+(u)∪u。节点u的吸收邻点集表示为N-(u)={v|(v,u)∈E,v∈V}，N-[u]=N-(u)∪u。由于本文研究的网络模型为BGB，所以定义节点u的邻点集为N(u)=N+(u)∩N-(u)。节点u的出度d+(u)等于N+(u)的大小，入度d-(u)等于N-(u)的大小，有效度d(u)等于N(u)的大小。ID(u)表示u的唯一识别符。

定义1(控制集) 若对于给定的球图G=(V,E)的一个子集S被称为G的一个控制集(dominating set，DS)，则对于任意节点u∈V-S，存在至少一个节点v∈S，使得u是v的控制邻点，即(v,u)∈E。若u在S中至少存在一个邻点，则称S是G的一个双向控制集(bidirectional dominating set，BDS)。

定义2(独立集) 对于给定的球图G=(V,E)的一个子集L，被称为G的一个独立集(independent set，IS)的充分必要条件是对于任意两个节点u,v∈L之间不存在双向边。u的独立邻点集表示为NID(u)。

定义3(极大独立集)L是图G的一个极大独立集(maximal independent set,MIS)，当且仅当L是G的一个独立子集并且满足V中的任意一点加入到L中都不可能形成一个新的独立集。

定义4(连通控制集) 给定一个有向球图G=(V,E)，子集S被称为G的一个连通控制集(connected dominating set ，CDS)，则S必须满足以下两个条件：

①S是G的一个双向控制集；

② 由S导出的子图G[S]是连通的，即G[S]中的任意两点之间都至少存在一条路径，使得两点之间可以相互传输信息。

如图1所示，一个有向连通球图由7个顶点和8条边组成。图1中没有箭头的实线表示双向边，带有箭头的虚线表示单向边，如(1,2),(3,4)。三角节点集{3,5,6}是该球图的一个连通控制集，通常标注为红色；圆形节点表示被控制的节点，通常标注为黑色。作为连通点的斯坦纳节点通常标注为蓝色。本文定义算法中的蓝红分量是指由蓝色和红色节点组成并且忽略掉蓝色节点之间的连通性所导出的一个连通分量。

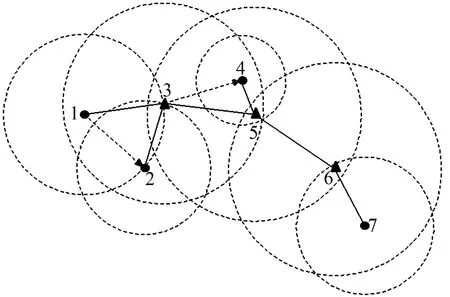
图1 具有双向链接的球图(BGB)

基于上述知识，本文提出了一种基于能量选择的三维异质无线传感器网络CDS构造算法ESA。ESA算法主要考虑CDS的大小和节点的传输功率，目的都是为了减少网络通信开销，节约能源，延长网络寿命。

2 能量选择算法ESA

一般来说，在单位球图G=(V,E)中，构造一个图G的近似最小连通控制集通常采用两步法：第一，找到图G的一个极大独立集S；第二，在S中添加一些额外的节点作为连接点，从而获得图G的一个连通控制集。所以极大独立集的上界对于求解CDS的近似比是非常重要的。本文提出的算法与其他算法最大的不同之处是节点可以自己调整它们的传输半径。能量选择算法ESA包含三个步骤：

① 选择每个节点的最优传输半径；

② 利用贪婪算法构造一个极大独立集，也是一个双向控制集；

③ 利用斯坦纳树连通控制集里的节点形成一个连通控制集。

输入一个有向球图，球图中的点都是随机分布在指定区域，每个节点的传输半径也是随机分配的。事实上，如果稍微调节一下每个节点的传输半径，从而使对应的每个传感器都能连接更多的传感器，这是很有意义的。因此，在下文中的算法ESA1中，每个节点都需要选择自己的最优传输半径。对球图中的每一个节点，根据贪婪策略并且按照下面定义的能量选择函数去重新设定传输半径。在连通控制集的构造过程中，采取染色的方法来区别不同子集的节点。为了便于分析，将能量选择算法ESA分解成算法ESA1 和算法ESA2。

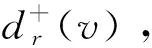
由定义5可知，节点v的最优能量函数为：

节点选择最优能量函数的半径为：

rbest(v)={r|Er(v)=Ebest(v)}。

假如输入一个连通的有向球图G=(V,E)，输出一个新的连通的有向球图G′=(V,E′)，则算法ESA1的步骤如下：

Step1：初始化，E′=∅；

Step2：对任意节点v∈V都赋予一个最优能量函数半径r(v)=rbest(v)；

Step3：对任意节点u∈V，而w∈V-u，如果dist(u,w)≤min{ru,rw}则有E′=E′∪(u,w)；

Step4：返回G′=(V,E′)，算法结束。

算法ESA1的输出图G′=(V,E′)是一个根据节点的最优能量函数构造的一个节点集不变但是边集变化的一个新的有向图。

在算法ESA1的基础上，假如输入一个连通的有向球图G′=(V,E′)，输出一个连通控制集S，则算法ESA2的流程如下：

Step1：初始化参数S=∅,W=∅,B=∅，所有的节点都为黑色；

Step2：当V≠∅时，选择一个有效度最大的点u∈V，有效度相同的情况下选择ID最小的节点，将它染成红色，并将u的邻点都染成灰色，S=S∪{u}，V=V-N[u]，W=W∪N(u)；

Step3：当V=∅时，循环结束。否则，返回step 2；

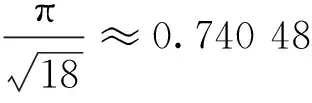
Step4：如果能够找到一个至少有i个红色邻点的节点u∈W，i=K到2，K=0.779 63(2k+1)2并且这些红色邻点属于不同的蓝红分量，则将u染成蓝色，W=W-{u},B=B∪{u};

Step5：当找不到这样的节点时，结束循环。否则，返回step 4；

Step6：L=S∪B，即将极大独立集和斯坦纳节点集并起来得到一个连通控制集L；

Step7：返回L，算法结束。

3 能量选择算法理论分析

在这一部分，详细分析了算法ESA1与ESA2的性能，并证明了CDS的性能比。

引理1算法ESA1中基于能量函数构造的新有向球图G′=(V,E′)仍然是连通的。

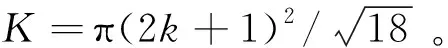
想要求得CDS的大小，还需要知道连接点的个数，在算法ESA2的第4步，本文采用最小斯坦纳树的方法，用尽可能少的斯坦纳节点来连接极大独立集中的节点，从而得到图G的一个连通控制集。并且还证明了该连通控制集与最优解的近似比为(K+1+ln(K-1))opt+1。在连通控制集的构造过程中，为了便于分析，本文采取染色的方法来区别不同子集的节点，将图G的极大独立子集S中的节点都染为红色，S的邻点集都染为灰色，斯坦纳节点集B作为连接点都染为蓝色。

定理1假设|B|≤(2+ln11)opt代表基于给定的MIS上的一个最优斯坦纳树，集合B是由算法ESA2中生成的斯坦纳节点集，则|B|≤(2+ln11)opt，opt表示MCDS的最优解的大小。

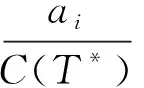
(1)

推导得：

(2)

(3)

结合式(1)～式(3)，对于任意i，可得：

(4)

ak≤ak-1-1≤…≤ah+1-(k-h-1)，

(5)

进一步可以推导出：

ah+1≤2C(T*)，

(6)

因此，

k-h≤2C(T*)，

(7)

注意，a0是初始的所有连接分量，由引理2得，BGB上任意一点最多有K个独立邻点，所以每加入一个蓝色节点最多可以连通K个连通分量，也就是最多减少(K-1)个连通分量，因为它本身又构成了一个新的更大的连通分量。因此：

(8)

(9)

综上所述，

|B|≤h+2C(T*)≤(2+ln(K-1))C(T*)。

(10)

因为MCDS也可以连接MIS，所以斯坦纳树问题的最优解的大小不可能超过MCDS的大小，即(2+ln(K-1))opt。因此在算法ESA2的第二阶段，本文最多选取(2+ln(K-1))opt个斯坦纳节点来连通MIS，即|B|≤(2+ln(K-1))opt，K=0.779 63(2k+1)2。

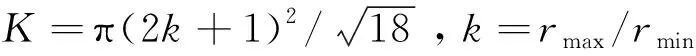
证明算法ESA2生成的CDS由两部分构成：极大独立集S和斯坦纳点集B。在ESA2的第一阶段，根据引理2，知道极大独立集的上界是(K-1)opt+1，K=0.779 63(2k+1)2，G′表示G′的MCDS的最优解大小。在第二阶段，本文采用斯坦纳树的方法来解决MIS的连通性问题，通过构造一个斯坦纳树来连接极大独立集中的节点。由定理2可知，ESA2中生成的斯坦纳节点集|B|≤(2+ln(K-1))opt。因此在第二阶段，最多选取(2+ln(K-1))opt(2+ln11)opt个斯坦纳节点来连通MIS。

综上所述，由算法ESA2生成的连通控制集L的上界为|L|≤|S|+|B|≤(K-1)opt+1+(2+ln(K-1))opt≤(K+1+ln(K-1))opt+1。

4 结语