道路限行的城市配送路径优化方法设计

何玉兰

（重庆交通大学交通运输学院，重庆 400041）

1 配送优化模型的构建

1.1 问题描述

有关城市货车交通管制相关的配送优化研究能够看成是对存在时间窗约束影响下的车辆调度研究的深层次扩展：由单个配送中心，选择多辆货车对若干个需求点完成必要的送货服务支持，并且在各个需求点时间窗、需求量与位置约束以及车辆载重以及通行时段与路段的情况下，更加科学合理地确定行车路径，由此获得配送最优的效果。

本文实现模型构建期间涉及的目标要素对应是：

（1）车辆数最少：为能够更好地与客户需求相符，各个企业都需要配备充足的车辆来保障送货任务顺利实施；（2）行驶距离最短：车辆的行驶距离与企业需要投入的配送成本有很明显的正相关联系，而且道路通行以及油耗等都与行驶距离密切相关，故而将行驶距离确定为最短的目标能够更大程度上达成配送成本最少的功能目标；（3）碳排放最低：政府推出通行管制的目标就是降低车辆通行，减少污染影响。

为能够顺利达成如上目标，在实现配送优化分析期间还需要重视下述条件约束：

（1）各个配送线上需求点的总体货物需求与车辆的最高载重量相符；（2）各个需求点相关的需求量都能够获得有效满足，并且仅仅是单辆车对其实施单次服务支持；（3）配送车辆经配送中心发出，配送完成后回归配送中心；（4）不得在进行路段内行车；（5）管制时段内车辆维持等待情况。

1.2 变量与参数

针对配送相关的有向连通图G=（N，M）而言，其呈现出下述特征情况：mij表征需求点i与j两者间的弧，全部弧选择M加以表征；顶点0表征的是配送中心位置，顶点1，2，……，n表征的是需求点位置，包含顶点0的时候全部顶点的集合表征是N，即可得N=｛0，1，2，……，n｝；不包含顶点0的时候，全部顶点的集合表征是C，即可得到C=｛1，2，……，n｝；mij表现的是时间值tij以及其距离值dij，前者表征的是两个需求点i与j需要的运输时间情况；需求点i位置需要的服务时间表征是si，而且需求量对应表征是qi；V=｛1，2，……，k，……，K｝表征的是全部车辆合集，其中Qk表征的是车辆k能够达成的最大载重量；E表征的是禁行路段所在的合集，能够满足M∩E=E；其中，[Rb1，Re1]表征的是早高峰期间的管制时段，[Rb2，Re2]表征的是晚高峰间的管制时段，R表征的是管制时段内全部限行路段合集，存在R∩E=Φ，M∩R=R的条件约束。此外，选择α表征单位运输期间的距离变动成本情况，β表征的是单位车辆开启需要的固定成本 情况。此处，dij，tij，qi，si，Qk，Rb，Re，α以及β对应都是非负数的存在。

在此模型内存在决策变量xijk，针对存在的弧mij以及车辆k而言，xijk=1，此时车辆k由其需求点i来到j；反之，xijk=0。

1.3 模型构建

目标函数：

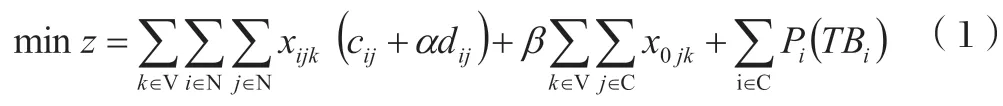
约束条件：

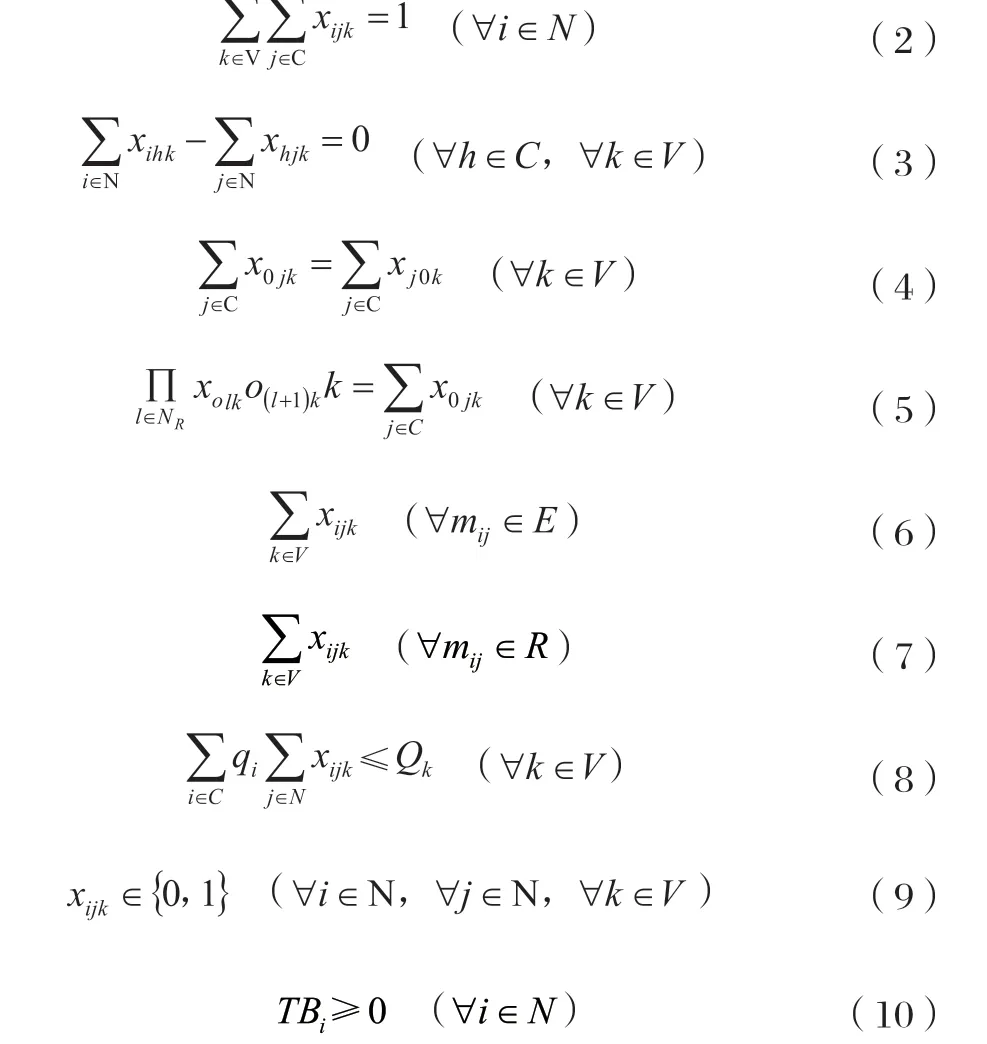
式（1）表征的是配送总成本最低，其涉及碳排放、车辆行驶距离、车辆延误惩罚以及车辆启用四部分的成本内容；式（2）表征的是各个需求点仅能够被单辆车加以服务；式（3）与式（4）约束各辆车在出发后，实现相关的配送要求后再行返回配送中心；式（5）是避免所得规划内出现子回路的情况；式（6）表征的是不得在禁行路段内行车；式（7）表征的是不得在禁行时段内行车；式（8）表征的是各路径上需求量综合能够与车辆最大载重相符的要求；式（9）表征的是决策变量呈现出来的整数化约束影响；式（10）表征与到达时间相关的非负性约束影响。

2 基于道路限行的混合遗传算法设计

2.1 初始种群生成

为保障初始解能够在其可行域内呈现出随机分布状态，需要设计获得与此种群生成相关的启发式规则。假定N表征的是种群规模情况，Ak表征的是第k条配送链情况，Akw表征的是与该链相联系的第w个客户，假定客户集合B=C并且Mw表征从第w个客户（配送中心）开始后能够达到集合B相关的客户情况，假定此处的变量k=1，如此就能够将规则表征是：

Stepl：如果B=Q5规则符合，就结束执行。反之，就继续执行操作；

Step2：于Mo内按照1/|Mo|概率的方式随机选定客户i，将其于B内移开，确定w=1，Akw=i。

①于Mo内按照1/|Mo|概率的方式随机选定客户i，将其于B内移开，确定w=w+1，Akw=i；继续②；

此处Ak对应着的是配送路径情况，k对应着的是被调度车辆情况。

2.2 适应度函数

当个体所得到的适应度值更高的情况下，则算法具备更好的性能。鉴于管制影响下的配送优化本质上是最小化问题，即获得最小的配送成本，目标函数值对应着的就是效用值求和，优劣解相差的数值并不高。为确保目标函数能够更好地转换适应度的情况，此处选定目标函数值对应着的倒数充当其适应度函数，明确f=1/z。

2.3 选择操作

本文用到的选择策略是最佳个体保留以及轮盘赌，全部个体参照其适应度情况由大到小加以排列，并且适应值最大的个体复制为下一代，由此确保最优个体能够在遗传期间继承下去，其余的个体则参照轮盘赌的情况加以选择，得到其适应度和值，单一个体相关的概率情况对应是，获得其累计概率由此获得随机数rand，如果出现pi-1＜rand≤pi就需要将个体i选出到下一代，反之，就继续操作一直到与规模N要求相符。

2.4 变异操作

参照确定的变异概率Pm，选择需要的个体G，即：

Stepl：于其染色体内得到客户i与j，互换位置得到最新的G’，如果G`对应是不可行解，就需要放弃，继续Stepl。反之，继续Step2；

Step2：对比G与G'两者的适应度函数值情况，如果出现f（G）＞ f（G’），继续Step。反之，就接受G’，变异分析完成。

3 结语

本文针对货运交通管制影响下的城市配送优化情况展开分析，明确带时间窗作用的车辆调度能够归属到NP-hard的问题。由于专业经验积累以及时间等限制，本研究还存在诸多不足，后续将从以下方向深化：（1）考虑由多个配送中心实现联合配送安排；（2）实际工作期间，客户对货物需要多变，配送企业也需要安排更多车型配送，考虑多车型情况的配送方案使整个调度优化分析更贴合现实。