基于最小等待时间和图游走模型的RGV动态调度策略

徐海龙 刘树树 牛学果 司 睿 李梦璇

（1.兰州交通大学交通运输学院，甘肃 兰州 730070；2.兰州交通大学土木工程学院，甘肃 兰州 730070）

随着自动化技术和制造业的进步和发展，智能化、自动化、柔性化[1]为三个主要发展趋势。柔性作业车间调度以其以需定产和定制模式向顾客提供优质服务，车间产品加工的效率逐年提升，能更好地完成车间的生产计划。但是，传统的柔性车间调度策略往往忽略了加工产品的个体化差异以及单个产品每道工序之间的衔接问题，使得智能化机器设备没有得到充分利用。如果从单个产品工序之间的相互等待时间最小为切入点，可使调度策略得到优化，增加可行性。

目前有很多文献著述了关于柔性车间的调度问题，大部分趋于加工时间调整和多目标优化的动态调度[2-4]，以近似求得此NP难问题的最优解。然而，对于加工产品的工序衔接和时间顺序调整方面的文献相对不多。文献[5]针对模糊柔性车间调度问题，提出一种混合超启发式遗传算法进行求解。文献[6]针对虚拟制造网络中的车间调度问题，提出了一个非合作博弈调度优化模型。文献[7]为了实现机械加工车间的节能优化运行，建立了节能柔性作业车间调度模型。

本文主要基于图论知识进行建模，研究了CNC智能加工系统，分析论证了基于图游走和最小等待时间的调度模型和策略，同时，利用JAVA语言进行了多线程并行编程，模拟RGV的运行以及各个CNC工作台的状态，验证调度策略的可行性和相对高效性，评价系统的作业效率。

1 问题描述和数学模型

1.1 问题描述

智能车间加工系统[9]主要是由数台计算机数控机床（Computer Number Controller，CNC）、1台固定轨道自动引导车（Rail Guide Vehicle，RGV）、1条RGV固定轨道、2条分上下料的传送带等设备组成。RGV是一种智能小车，可根据特定指令自动运行。并利用自带的机械手臂、手爪等装置，完成产品的上下料、清洗等作业。对于该系统，需要设计合理实用的调度策略，提高平台工作效率以增加产出率。本文针对一道工序、两道工序加工和CNC故障情况进行研究，建立调度数学模型并设计求解算法，并用JAVA进行仿真，验证了其可行性。

1.2 模型建立

将8台CNC假设为8个节点，由此构成一个图，边表示RGV在两节点间可移动。在RGV小车在每进行一次作业，其他的CNC工作台发出请求后，经过筛选和权值的判断，做出相应的命令执行。在车间调度问题中，它是一个多项等式和不等式约束下的组合优化问题。从计算时间的复杂度看，它可以看作是NP难问题，随着调度规模数的增加，问题的可行解的数量呈指数级增加。

目标是在一定时间内要获得最大的加工产品数，就要使得总的等待时间越少。总共生产的总共件数为：

每台CNC生产的台数由（2）式决定：

由（1）式：

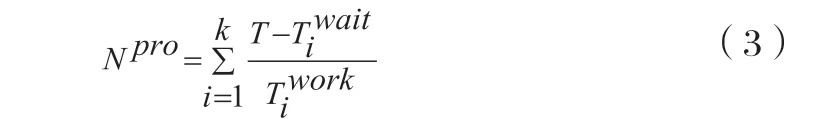
目标追求最大化N pro，等价最小化，所以最小化目标函数为：

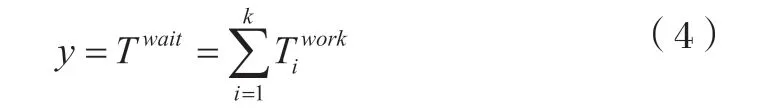
式（1）～（4）中：N pro—加工总产品数（个）；k—CNC台数（台）；ni—第i台CNC加工产品数（个）；T—一个工作周期（s）；—第i台CNC等待时间（s）；—第i台CNC工作时间（s）；Twait—总的等待时间（s）。当该系统加工两道工序时，只需更改目标函数中的相应等待时间。如式（5）：

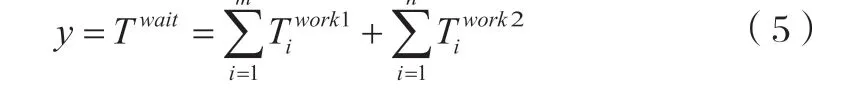
当该系统加工工序发生故障时，如式（6）：

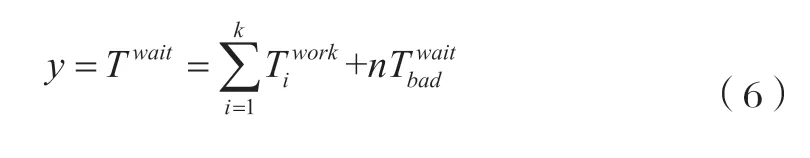
2 求解策略算法设计

针对单工序产品，图邻接矩阵的权值为节点间小车移动和上下料时间之和。当有1台CNC发出请求时，RGV对该CNC进行相应作业；当有多个节点发出请求时，按照总体最小等待时间的策略选择RGV移动的位置。RGV在接收到两道工序混合发出的请求之后，按照考虑了不同刀具平台的等待时间，根据紧后工序依赖于紧前工序的完成的均衡原则和权值进行判断，从而选择最优的路径。

对于系统故障的模拟和处理时间，本文均采用了生成随机数的方法。规定当随机产生的数小于0.01时，CNC便会发生故障。经人工恢复（10～20 min）后重新进入选择队列之中。以单工序为例，如图1所示，多台CNC发出请求，选择边权最小的路径，移动至相应CNC。算法设计如下：

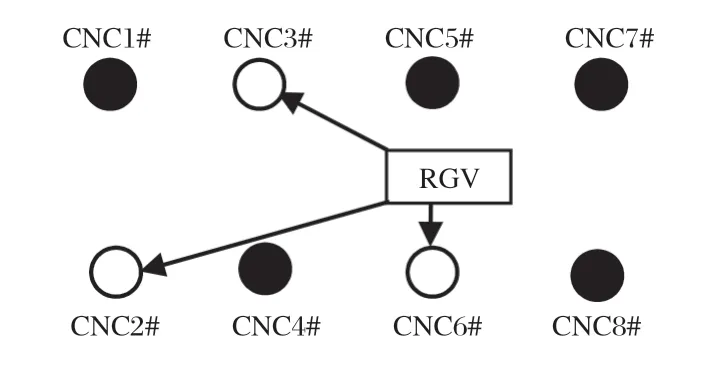
图1 三个CNC发出请求状态

（1）相关参数初始化，请求队列R={1，2，…，8}，RGV在第一台CNC的位置Gp=1，加工产品数为i=0，相关时间记录表Tb，Artnum={0，0，0，0，0，0，0，0}//每台CNC计数。（2）获取当前系统的时间。为每个CNC上料，new workThread（k，art[k]）.start；// 启动工作并行线程。并记录相关CNC平台上下料的时间。（3）RGV.scan（R）；//扫描请求队列，若为空，则处于阻塞状态[10]，停止执行。否则，执行4）。（4）若R中只有一个元素为n，Ob=n；//找到下次工作CNC相应的编号。否则，从请求队列R={1，2，…，8}中找到RGV智能车移动时间和对应CNC上下料时间最短的元素j。Ob=j；//找到权值最小元素。（5）RGV.move（ob，tm）；//RGV智能车用时tm移动到ob对应的CNC。RGV位置Gp=ob。（6）RGV.get（tq，Tb，art[ob]，td））；//RGV智 能车以tq的时间给ob对应的CNC上料，并在Tb表中记录上料开始时间。（7）RGV.put（tp，ob，Tb，tpc，i）；//RGV智能车以tp的时间给ob对应的CNC下料，并在Tb表中记录下料开始时间。i=i+1；new workThread（k，art[k]）.start；Artnum[ob]=i；//此时，i发生变化，多线程并行。（8）Tc=Sys.getCurrentTime（）；//获取系统当前时间。若Tc-Tbegin＜T，T为时间周期（取为8小时）转（3）。否则，转（9）。（9）结束。

3 系统作业效率评价

在评价系统的作业效率时，本文采用的是产品模拟加工数量所用的时间与一个加工时间周期的比值。其评价模型表达式如下：

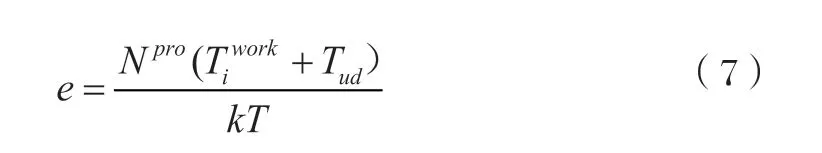
式中：Tud——上下料时间（s）；k——CNC数量（台）。

对于模拟加工产品数量，本文取3～5次模拟结果的平均值。做出该调度策略下不同参数的系统作业效率分析。经过JAVA仿真模拟运算结果如表1所示。

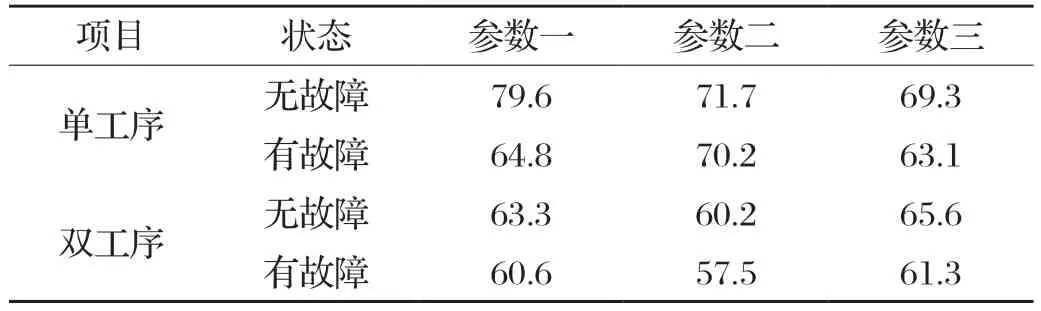
表1 不同参数系统作业效率统计表 /%

4 结语

基于图游走和最小等待时间建立模型，抽象8台CNC为图的节点，以RGV游走距离和上下料时间为图边权值，将NP难的调度问题，通过模型和求解策略，各阶段局部优化，最终达到整体近似最优。以图论的相关知识建立模型，比较切合实际CNC的工作状态。用JAVA多线程编程进行并行工作模拟，减少并验证了实际的调度时间。多次进行模拟，消除了故障的随机性。本文中大多数模型都是自行推导建立的，可以推广到柔性车间的调度、小工厂的车间生产、智能化的选择需求等问题。