基于核心素养的高中数学教学——以向量的线性运算为例

◎ 张鸿博

一、复习回顾，夯实基础

向量的线性运算是高中数学高一上学期必修四第一章第二节的内容，具有承上启下的作用，故应先复习回顾相关概念。

向量的定义、单位向量、零向量、相等向量、相反向量、平行向量等。

二、创设情境，引入课题

创设情境：2018年是改革开放40周年，在纪录片《厉害了，我的国》中，提到了港珠澳大桥，港珠澳大桥对珠三角地区的交通运输提供了巨大的便利。

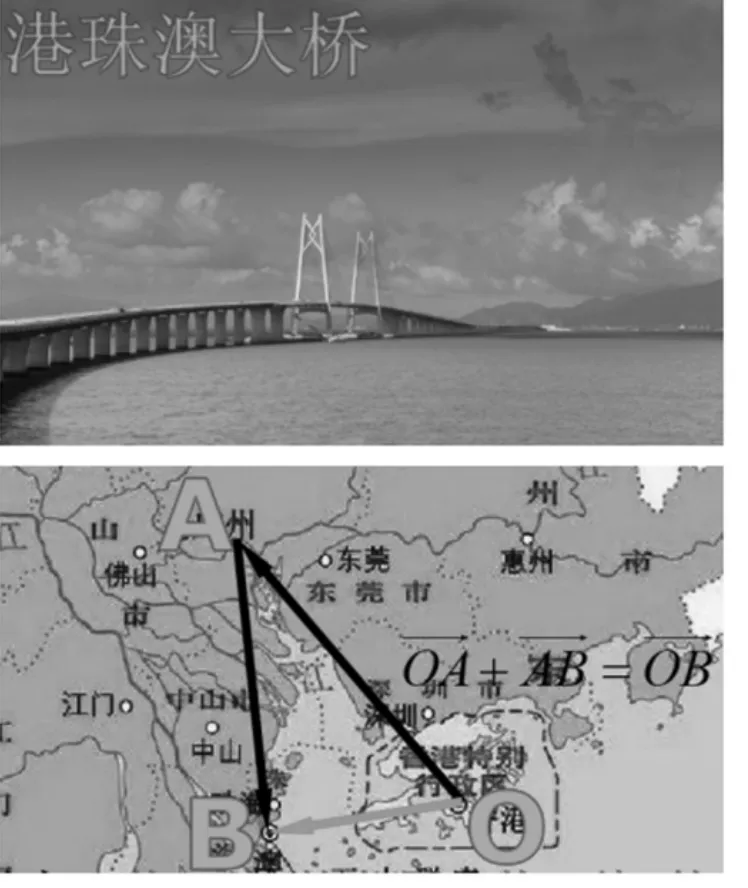
如图，在2018年以前，想要从香港到澳门，需要先作“香港到广州的位移”，再作“广州到澳门的位移”，才能到达终点。

而如今，我们只需要直接作“香港到澳门的位移”就可以到达终点，大大缩减了路上所需的时间。

如图，我们用字母“O”抽象地代表香港，用字母“A”抽象地代表广州，用字母“B”抽象地代表澳门，即先作“从O到A的向量”，再作“从A到B的向量”等价于“从O到B的向量”，在此处给出向量加法的定义：求两个向量和的运算称为向量的加法，即。

设计意图：通过创设情境，把数学与生活联系起来，引起学生的学习兴趣。另外，通过情境地引入，培养学生的数学抽象能力和数学建模能力。

三、问题引导，加深理解

问题1：如果两个向量没有相交，怎么做加法呢？

设计意图：引起学生思考，回忆“向量是自由的，可以移动的”，从而引出向量的三角形法则：首尾相接收尾连。

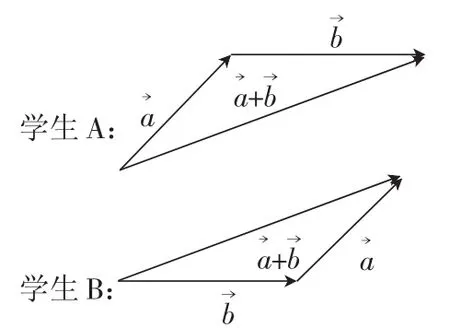
问题2：以上两位学生很聪明，都作出了向量的加法，可是不太一样，但结果相同吗？这说明了什么呢？

设计意图：通过不同的连接方式，却得到了相同的结果，启发学生与实数的加法进行类比，从而得到向量加法的交换律。

问题3：刚刚我们通过平移得到向量加法的交换律，不过这时的图形形成了一个平行四边形，联系物理知识，说说向量的加法还满足什么法则？

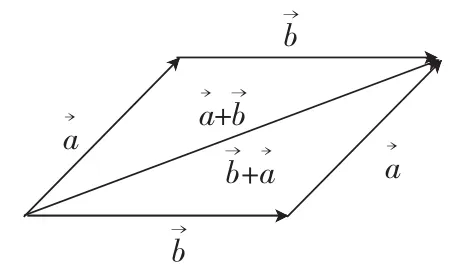
设计意图：向量的平行四边形法则是学生更加熟悉的一种向量运算法则，所以这里不过多阐述，特点：共起点连对角线。

问题4：向量的加法满足加法交换律，那么向量的加法还可能满足什么运算律呢？试画图说明。

设计意图：通过与实数加法运算律的类比，不难猜出向量加法的结合律，但作图说明具有较大难度，这里笔者选择找一个聪明的学生分享他的作图，其他学生看完恍然大悟。

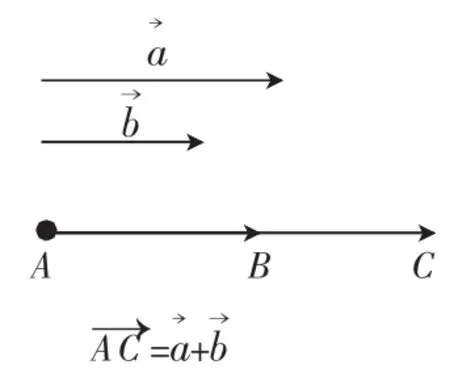
问题5：特殊的向量如何作加法运算呢？

(3)共线向量的加法：

①方向相同

②方向相反

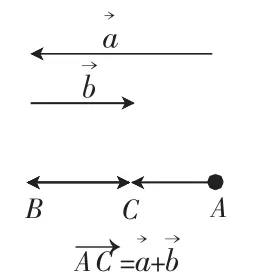
设计意图：从一般到特殊，扫除所有知识漏洞，形成本节课完整的知识体系。

四、例题精讲，展示共评

例1：如图，O是正六边形ABCDEF的中心，作出下列向量：

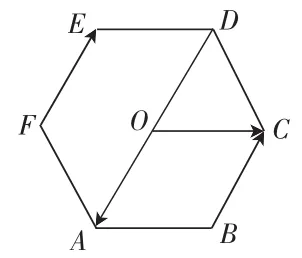
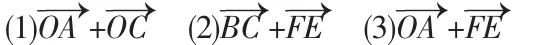
例2：计算下列向量的和：

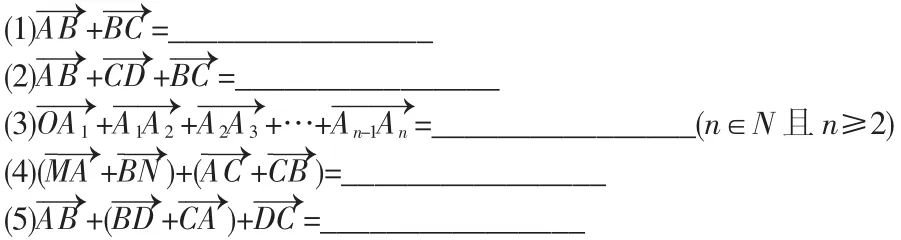
设计意图：从图形到字母，从具体到抽象，加深学生对向量加法的理解，层层递进，便于学生理解。

以上所谈仅是结合数学核心素养对“向量的线性运算”的一些思索，所涉及方面很有限，只有每节数学课有不同的思考和挖掘，认真处理好每节数学课的教学过程，才能真正使核心素养落到实处。