从设而求之到设而不求

◎ 王琳琳

在数学中，有一种可以与“方程思想”比肩的思想方法——“设而不求”。从字面意思上也不难理解他们之间的联系与区别：两者皆需设未知量，不同的是前者需将未知量分别求解出来，后者则只是将未知量作为“沟通”的桥梁，无需费力求解。这种解题思路，给人耳目一新的感觉，同时也可感受到数学之美。

案例一：设“K”法的妙用

在代数学习中学生会经常碰到连等式和连等方程的题，解决此类问题的一大法宝是解设“K”法。在学习比例式中的等比性质的证明时，这种方法给了我们很多的启示。

我们不妨可以这样大胆地说，凡是出现这样比例式的证明，设元时往往可以按比值设元，这体现了“化分为整”的数学思路，问题很快得到解决。

设“K”法非常灵活巧妙，在一些表面看上去无比例式的证明中也适用，例如：三角函数中的一道证明——如图：在Rt△ABC中，已知，求∠A的其他三角函数值。

思路一：(利用三角函数之间的关系)。

思路二：(设K法)

比较两种方法，前者容易想到，但是对于初学三角函数的学生来说，运算上要求高，容易出错，而且公式的记忆也比较难，易出现偏差。后者运算量小，思维量也不大，也很好地体现了数形结合的思想。

对于同类型的问题，如果做适当的变化，设“K”法能收获同样的效果。例：如图：将原题中添加一条AB边上的中线CD，加一条件，CD=5，其余条件不变，则这个三角形可解。我们来试一试。

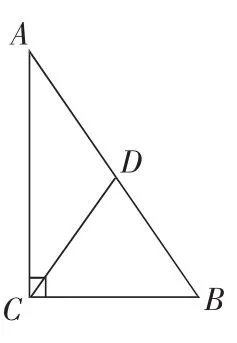
首先在上一题的解答中，三角的三角函数值可求，也即三个角可以表示出来，由于三角函数值不特殊，初中阶段我们尚且不会这种表示方法。

我们再来看边的求法。这里依旧可沿用设“K”法，∵CD=5，∴AB=10又

这些都是设“K”法的简单应用，在初中数学中，它是一种简单高效的方法。设K而不求K，体现了数学中的大智慧。

案例二：固定结构的化简

在学韦达定理的时候，我们知道，对于一元二次方程ax2+bc+c=0，若Δ≥0，则方程有两个实数根，不妨设为x1，x2，则有。

我们总结这类问题的求法，关键在于将式子整理成含x1+x2和x·1x2的结构，而无需将x1，x2各自求出，这也是“设而不求”的精髓所在。

这样的例子不一而足。我们可以看到“设而不求”的解题思路实际就是立足于数学中的整体思想。这种重要数学方法和技巧的掌握对于整个中学阶段的学习都有举足轻重的作用。到高中解析几何中的圆锥曲线中就经常要用到这种方法，它能在最大程度上优化解题思路，减少计算量，提高解题效率。可谓解题中不折不扣的“跳板高手”。