从2019年几道高考题谈万能公式的应用

安徽

谷留明

(作者单位：安徽省合肥市第一中学)

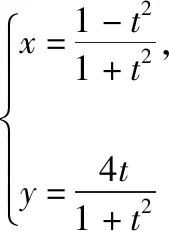
(Ⅰ)求C和l的直角坐标方程;

(Ⅱ)求C上的点到l距离的最小值.

( )

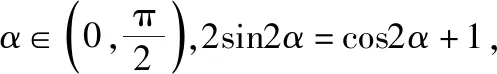
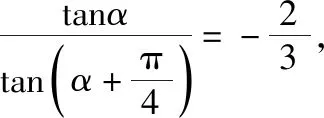
一、万能公式

二、真题分析

【引例1分析】由曲线C的参数方程消参可求直角坐标方程,如果单纯用代数运算消参,要么运算量较大,要么需要高超的运算技巧,而如果根据式子的结构能联想到万能公式,则非常简洁.

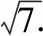
经安徽阅卷老师反馈,这道题得分率很低,只有极少数的同学运用了万能公式,使得整道题的解答畅通无阻；而没用到的考生绝大部分都迷失在代数运算中,没有求出C的直角坐标方程,从而第(Ⅱ)问也无从做起.

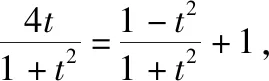
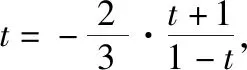
在引例2和引例3的解答中,可以将相关三角函数式的分母看作1,并逆代为cos2α+sin2α,再将分子、分母同时除以cos2α,实现弦化切.其实这就是万能公式的本质思想.

由以上分析,足见万能公式的重要性,虽不是必备知识,但若能熟练掌握,绝对如虎添翼,甚至能绝处逢源.以下阐述万能公式的证明与应用.

三、公式证明

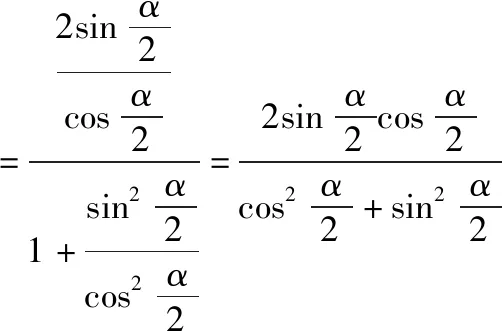
=sinα=左边.

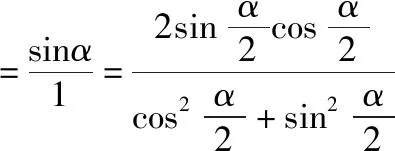
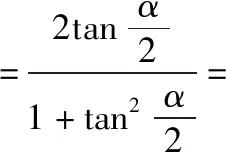
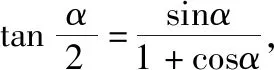
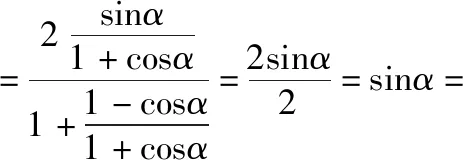
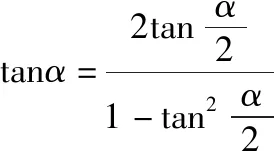
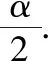
四、公式应用

(一)代数化三角

1.求轨迹方程

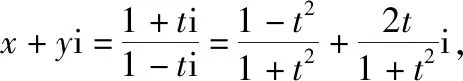
2.证明(不)等式

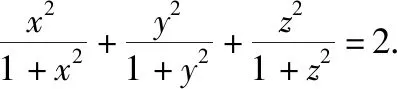
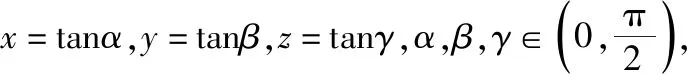
3.求函数值域

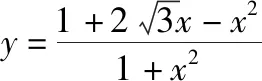
4.解不等式(方程)

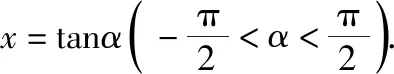
(二)三角化代数

1.求三角函数值

【例5】见引例2和引例3.

2.化简或证明

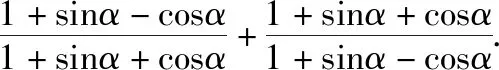
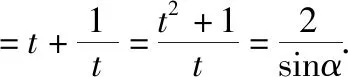
3.解不等式(方程)