一道双曲线离心率问题的多视角探究
甘肃
张 科 宋东荣
(作者单位:甘肃省兰州市榆中县恩玲中学)
众所周知,圆锥曲线是高中数学中的重点和难点,在高考卷的选择压轴题中常常涉及与圆锥曲线有关的问题,特别是对圆锥曲线离心率问题的考查.下面笔者对一道有关求双曲线离心率的问题从多个角度进行分析,以培养学生的推理论证能力和创新意识,促进思维能力和思维质量的提高.
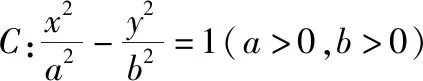
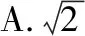
C.2 D.3
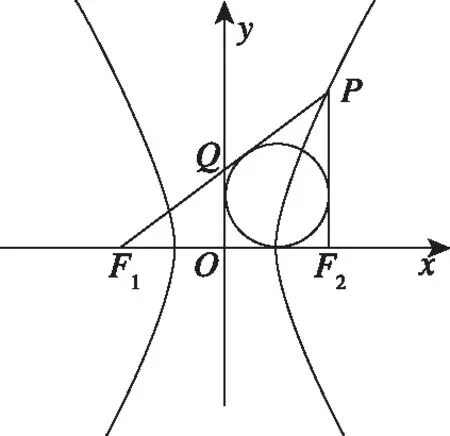
一、代数视角
在解析几何的学习中,我们经常使用数形结合的代数方法——坐标法来讨论问题,有助于让学生体会数形结合的思想方法,就此题用代数视角给出下面3种解法.
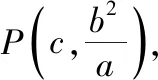
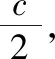
【赏析】此解法是常规解法,运用数形结合和直线方程有关知识使问题得以解决,培养学生的数学运算和直观想象等数学学科核心素养.
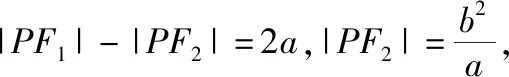
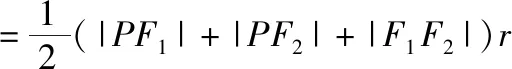
化简得c(ac+2a2-c2)=0,即ac+2a2-c2=0,两边同时除以a2得,e2-e-2=0,解得e=2和-1(舍).故选C.
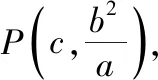
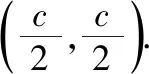
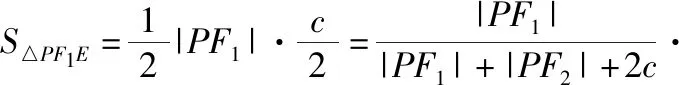
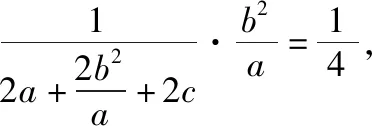
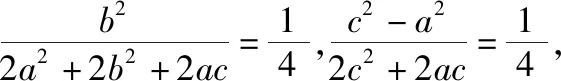
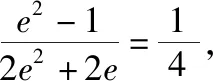
解得e=2和-1(舍).故选C.
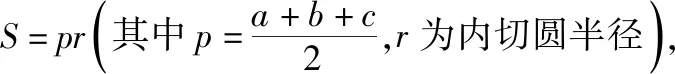
二、几何视角
解析几何的实质还是几何,所以我们要善于发现图形的几何特征,以便更好地处理问题和培养学生的几何直观能力,基于几何视角给出以下3种解法.
解法4:由直角三角形内切圆的性质可知,|PF2|+|F1F2|-|PF1|=2r=c,又由双曲线的定义得|PF1|-|PF2|=2a,两式相加得|F1F2|=c+2a,
即2c=c+2a,得到c=2a,解得e=2.故选C.
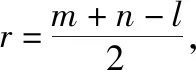
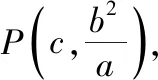
又因为PE过点E,
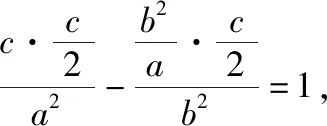
【赏析】此解法应用双曲线的光学性质和过双曲线上任意一点的切线方程的知识,使得问题的解决得心应手.
解法6:如图,设四边形OF2PQ的内切圆与边PF1,F1F2,PF2的切点分别为T,M,K,由双曲线的定义和切线长定理知|PF1|-|PF2|=|F1T|-|KF2|=|F1M|-|MF2|=2a,
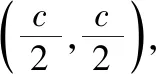
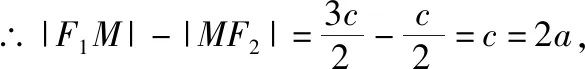
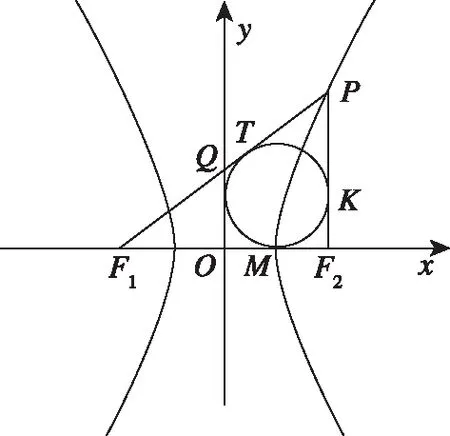
【赏析】此法应用了双曲线的定义和平面几何知识中切线长定理的相关知识,使问题得以解决,体现出应用几何法解决某些解析几何问题的简洁性和直观性,有助于学生的直观想象核心素养的形成.
三、结论视角
结论:内切圆的圆心横坐标一定等于|a|.
证明:如图所示,
∵|F1D|-|F2D|=|F1P|-|F2P|=2a=(c+xD)-(c-xD),
∴xD=a.
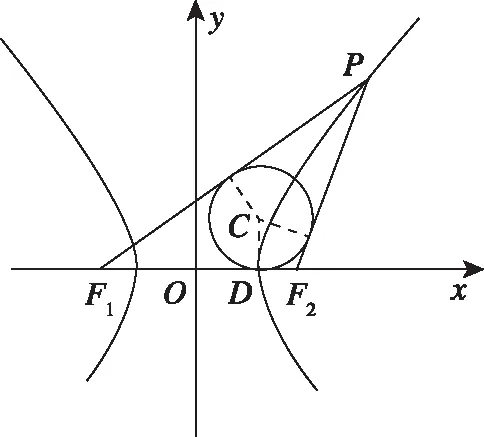
根据上面的结论,我们得到如下解法.
解法7:由双曲线焦点三角形的性质可知,△PF1F2的内切圆有且只有一个,且圆心的横坐标一定等于|a|,即四边形OF2PQ的内切圆也就是△PF1F2的内切圆.
又由题意知,内切圆同时与x=c和x=0相切,于是2a=c,即e=2.故选C.
【赏析】此法运用双曲线焦点三角形内切圆有且只有一个,且圆心横坐标一定等于|a|的结论.使解题过程更加简洁,也体现出“小题小做”.
四、几点思考
1.存在问题
从本道试题的测试结果分析:试题的得分率较低,学生不能有效地获取a,c的关系求出离心率,引发问题出现的根本原因与学生数学基础薄弱、运算能力差以及对解析几何题的恐惧心理有很大的关系,也与我们复习过程中“就题论题”,不能充分关注和激发具有生命活力的课堂有很大关系.
2.归纳小结
本题从不同的视角探究双曲线的离心率问题,总结出求离心率的三种思路.
①求出a,b,c三个量中的任意两个,然后利用离心率的计算公式求解;
②求出a,c或a,b或c,b之间的关系,然后利用离心率的计算公式求解;
③构造出关于离心率e的方程求解.
思路的归纳总结有助于教师的教与学生的学,教学中能根据题目的结构特征探索出解决问题的相应模型,既培养了学生的数学建模能力,同时也提升了教师数学建模的能力和意识,教学能更有效地助推学生思维的发展.
3.研究示范


