冬小麦田多花黑麦草田间分布型及抽样方法研究

曹 瑛,金平涛,杨 非,张宝强,陈小平

(1.西安市农业技术推广中心，陕西 西安 710061；2.周至县植保植检站，陕西 周至 710400；3.蓝田县农业技术推广中心，陕西 蓝田 710500；4.西安市长安区农业技术推广中心，陕西 西安 710100)

小麦是陕西关中地区的主要粮食作物，年种植面积约70万hm2，麦田杂草是影响小麦生产的一大类有害生物。20世纪末，多花黑麦草(Lolium multiflorum)作为牧草被引入关中地区，由于其适生性极强，逐渐侵入邻近麦田，继而扩展蔓延，目前已成为西安市、宝鸡市、咸阳市、渭南市、铜川市等麦区的优势禾本科杂草，严重发生田损失可达50%以上。为此，笔者在多年跟踪调查记录的基础上，对其田间分布型及抽样调查方法进行了研究，以期为多花黑麦草精准监测及提高防效提供依据。

1 材料与方法

1.1 田间分布型及取样方法

1.1.1 调查方法 2016年在长安区、高陵区、蓝田县选取多花黑麦草中等至偏重发生的8块冬小麦田，麦田面积2～3.8×667 m2，由于小麦苗期与多花黑麦草难以分辨，调查误差较大，因此选择在5月上旬小麦灌浆期调查杂草茎数。每块田从地头确定等距离的5行，每行从地头30 cm处开始，根据地块长度确定间距相同的10个样点，共50个样点，每样点0.33 cm×0.33 cm(做成铁丝方框以便于精确计数)，按顺序将杂草茎数记录在方格纸上。

1.1.2 计算方法 主要有:

(1)分布型测算。①计算样本数n、样本x的平均密度M、方差S2,并计算扩散系数C(C= S2/M)；扩散型指数Iσ。(Iσ=[n×(∑fx2-∑fx)]÷(∑fx×(∑fx-1))]；负二项分布K值(K=M2/(S2-M))；CA指标(CA=1/K)；平均拥挤度m*(m*=M+(S2/M-1)和聚集度指标(m*/M)，根据各项聚集度指标判断分布型。②用分布频次拟合、 Taylor聚集特征指数公式中的“b”值(S2=aMb,a、b为待估计参数，a为抽取因素，b为聚集特征的指数。当b→0时，为均匀分布，b=1时，为随机分布，b>1时，为聚集分布)、平均拥挤度(m*)与平均密度M的回归分析(m*=α+βM)做进一步检验。

(2)聚集原因分析 。根据聚集均数：λ= M ×γ/2K，其中，γ为自由度等于2K、概率为 0.5 时的卡方值( χ2) 。当λ<2时，聚集原因是由某些环境因素如人为行为、气候、土壤及植株生育状况等所致；当λ≤2时，聚集原因由自身特性或与环境因素共同作用所致。

(3)抽样方法选定。 在原始数据的方格纸上，每块田取5～12个样点( 每点 0.33 m2) ，选择随机五点、单对角线、双对角线、“Z”字形和棋盘式 5 种抽样方法，计算平均每样点杂草数，与相应田块50样点的平均密度比较，计算每种抽样方法的平均误差率，从而确定最佳抽样方法。

(4)理论抽样数的确定 。根据理论抽样数计算公式：n=t2/D2((α+1)/M+β-1)。其中: t为概率保证值，D为允许误差，α、β为平均拥挤度m*与平均密度M回归式中的参数。将概率保证值t定为 1.96，在允许不同误差D(= 0.1，0.2，0.3 ) 的情况下，计算理论抽样数。

2 结果与分析

2.1 分布型测定与检验

2.1.1 分布型测定 由聚集度指标(表1)及分布型标准(表2)分析得出，8块田多花黑麦草扩

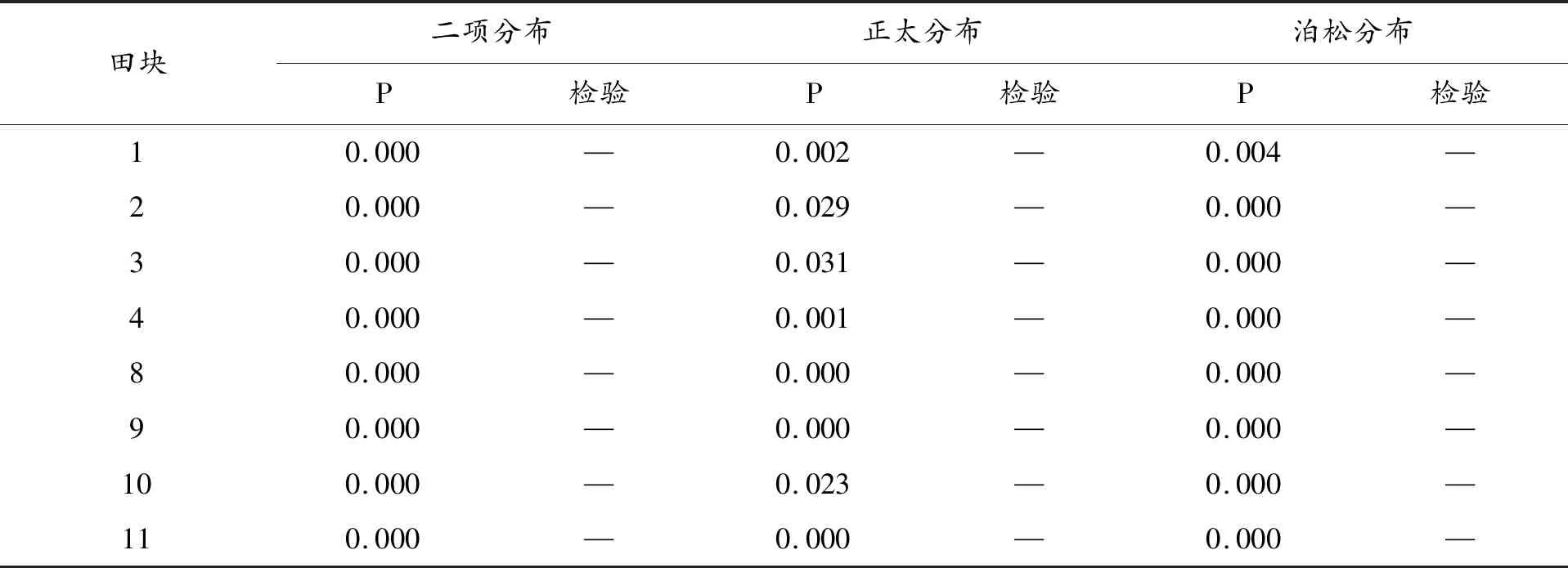
散系数C>1，CA>0,扩散性指数Iσ>1,负二项分布0

表1 麦田多花黑麦草聚集性指标及聚集均数

表2 聚集度指标分布型值的标准

2.1.2 分布型检验 主要有:

(1)调查的8块田均不符合二项分布、正太分布及泊松分布(表3)。

(2)Taylor 分析得出，方差(S2)与平均数(M)的对数关系为lgS2=-0.351+1.843lgM(r=0.724)，b=1.8431>1，多花黑麦草在麦田为聚集分布。Iwao分析中平均拥挤度(m*)与平均数(M)所建立的直线回归方程为m*=3.5327+1.1008 M(r=0.956)；α=3.5327>0，β=1.1008>1，由此可知，多花黑麦草分布的基本成分是个体群，为聚集分布，而且呈一般的负二项分布，聚集是由于多花黑麦草种群本身的群集性引起。

表3 麦田多花黑麦草分布型频次分布检验

注：-表示不符合(P<0.05)，*表示符合(P>0.05)。

2.2 田间抽样方法

5种抽样方法中棋盘式取样、“Z”形取样与实际密度的平均误差率分别为10.85%、11.87%，与实际密度最为接近，而随机五点、单对角线、双对角线取样误差率均在15%以上(表4)，因此宜采用棋盘式取样或“Z”形取样方法。

表4 多花黑麦草不同抽样方法的误差率

2.3 抽样数的确定

在概率保证值t为 1.96，允许误差D(= 0.1,0.2,0.3 ) 的情况下，多花黑麦草发生密度越大,理论抽样点数越少；发生密度越小，理论抽样点数越多(表5)。

表5 多花黑麦草不同密度下的最适抽样样点数

3 结论

通过对多花黑麦草田间分布型及取样方法的研究得出，多花黑麦草的空间分布为聚集分布，分布基本成分为个体群，聚集是由多花黑麦草自身落种特点所致。经随机五点、单对角线、双对角线、“Z”字形和棋盘式 5 种抽样方法与多花黑麦草实际发生密度的误差率计算，棋盘式和“Z”字形误差率较小，可作为田间抽样方法。根据多花黑麦草理论抽样数的计算，在允许误差0.3时，密度约5～15茎·0.33 m-2，抽样数为24个以上，密度约15～35茎·0.33 m-2，抽样点数为10个以上，密度约35茎·0.33 m-2以上时，抽样点数6～10个即可。在麦田化学除草时，亦可根据多花黑麦草的分布型特征进行施药，杂草发生量大时，可用药剂及用水量的最大限量，在均匀施药的前提下，适当照顾杂草聚集部分。