基于改进鲨鱼优化算法的倒立摆自抗扰控制研究

吴 敏，肖志坚，尚 猛

(1.浙江东方职业技术学院 数字工程学院,浙江 温州 325000；2.岭南大学 经营学院,韩国 庆山 385141)

0 引 言

旋转倒立摆是一类具有强耦合性的非线性系统，通常作为各类控制算法的检验装置。由旋转倒立摆的运动方式与机械臂旋转轴运动和火箭飞行原理有很大的相同之处，因此对于倒立摆的控制策略研究有着很深远的工程意义[1]。旋转倒立摆通常由两个可以自由移动的旋转杆组成，具有两个自由度且两个自由度之间具有很强的耦合性和非线性，因此对于控制算法提出了更高的控制要求[2]。王浩等提出一种分数阶PID的控制策略[3]，解决了传统PID控制精度不高的问题。彭继慎等提出一种倒立摆的神经网络自适应滑模控制[4]，有效的提高了控制精度，但对于控制过程中的外界扰动影响，未做很好的处理。因此本文提出一种基于自抗扰的控制策略。

自抗扰控制[5](Active Disturbance Rejection Control，ADRC)是韩京清教授提出的一种具有强抗扰动能力的控制器，其优点在于控制过程中不依赖被控对象精确的数学模型，对于处理具有强耦合非线性的控制模型具有较强的控制精度。但缺点在于，非线性自抗扰控制器具有多个控制器参数，且参数之间具有很强的耦合性，在实际控制过程中，控制参数整定的是否精确很大程度的决定了自抗扰控制器的控制精度。因此为了使自抗扰控制器可以更广泛的应用与实际控制中，国内外越来越多的研究学者提出了多种自抗扰控制器参数的整定方法。刘福才等通过混沌粒子群算法对自抗扰控制器进行参数整定，很大程度提高了控制器的控制精度[6]。周宜然等提出了一种改进的遗传算法，避免了遗传算法陷入局部最优的问题，提高了控制器的抗扰动能力[7]。刘晓丽等提出了一种基于蚁群优化算法的自抗扰参数整定方法，但算法在迭代过程中会出现早熟收敛的情况，在一定程度上会对控制器的控制精度有所影响[8]。肖静等提出一种基于免疫自整定的ADRC研究[9]。刘朝华等提出一种基于免疫双态微粒群的混沌系统自抗扰控制[10]。以上方法均在一定程度上提高了自抗扰控制器的控制精度，有效的整定了控制器参数，但也存在一些不足。因此本文提出一种基于改进鲨鱼优化算法的自抗扰控制器参数整定策略。

针对传统鲨鱼优化算法[11]易陷入局部最优的问题，本文通过对立学习初始化和均匀变异策略对鲨鱼优化算法进行改进，提高了算法的收敛速度和收敛精度，并通过改进后的鲨鱼优化算法在线整定自抗扰控制器控制参数，提高了控制器的控制精度和抗扰动能力。最后以旋转倒立摆为被控对象，验证了本文所提方法的有效性。

1 自抗扰控制

自抗扰控制器的主要有三个组成部分，分别为微分跟踪器(Tracking Differentiator，TD)、非线性反馈控制率(Nonlinear State Error Feedback Control Law，NLSEF)以及自抗扰控制器的核心组成部分，扩张状态观测器(Extended State Observe，ESO)。以旋转倒立摆为被控对象，其控制结构如图1所示。

图1 旋转倒立摆自抗扰控制框图

图中θ和ψ分别为旋转倒立摆的摆角和转角。其中控制倒立摆摆角和转角的自抗扰控制器结构相同，因此以控制摆角的自抗扰控制器为例，其数学模型为

(1)

式中，θ1(k)为摆角角度，θ2(k)为摆角速度。同理，对于转角的TD而言，ψ1(k)为转角角度，ψ2(k)为转角速度。r为快慢因子，h为步长。ESO估计被控对象的各阶状态变量z1，z1，z4，z5以及总扰动的实时作用量z3和z6，同样以摆角的ESO为例，其数学表达式如下所示：

(2)

式中，β01，β02和β03为修正系数，很大程度影响ESO的观测效果。NLSEF对误差eθ1和eθ2进行非线性组合，并输出控制信号uθ0，对误差eψ1和eψ2进行非线性组合，并输出控制信号uψ0。以摆角的NLSEF为例，其数学表达式为

(3)

式中，β1和β2为控制系数，很大程度影响ADRC的控制精度。fal(·)函数为一类非线性函数，代表输出误差校正率，其表达式为

(4)

因此，对于摆角的ADRC而言，需要整定的参数有β01、β02、β03、β1和β2。对于转角的ADRC而言，需要整定的参数有β04、β05、β06、β3和β4。通过大量实验表明，其余参数对控制器精度影响不大，因此可人工调节。

2 改进的鲨鱼优化算法

2.1 基本鲨鱼优化算法

基本鲨鱼优化算法是模拟鲨鱼觅食所提出的一类群智能优化算法。在基本鲨鱼优化算法中，每一条受伤流血的鱼均可视为鲨鱼的猎物，由于每条受伤的鱼的位置均不固定，因此鲨鱼优化算法在可行域内的种群初始化行为表现为随机性，其公式为

(5)

(6)

鲨鱼在游动过程中会存在一定的惯性，因此鲨鱼每个阶段的速度均取决于上一个阶段的速度，并且鲨鱼在游动过程中会保持在一定的速度范围内，因此定义鲨鱼优化算法每个维度的速度更新公式为

(7)

其中，i=(1,2,…,NP)；j=(1,2,…,ND)；OF为目标函数。上标k表示鲨鱼当前的运动阶段。由于鲨鱼可能无法到达每个阶段的最大速度，因此设定ηt∈[0,1]。R1和R2为均匀分布在[0,1]之间的随机数。αt为惯性系数，是[0,1]之间的随机数并在阶段t内为恒定值。βt为t阶段的速度限制率。

(8)

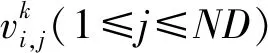
除此之外，鲨鱼还会通过特有的旋转移动进行猎食，其运动轨迹不一定为一个标准圆形。从优化角度来看，鲨鱼的旋转前进可以使鲨鱼在每个阶段实现本地搜索。以此来找到更好的候选解决方案。这种位置的搜索公式为

(9)

式中，m为位置搜索中每个阶段的猎物的数量。鲨鱼会向具有更强气味的猎物进行移动，并继续搜索路径，这一特点在SSO算法实现如下：

(10)

2.2 鲨鱼优化算法的改进策略

首先，对于群智能优化算法而言，种群初始化范围的大小在一定程度上决定了算法的寻优精度。由于传统鲨鱼优化算法在初始阶段并没有任何对全局最优解的先验认识，导致初始化阶段的鲨鱼种群均匀分布在搜索空间内。然传统鲨鱼优化算法的寻优策略是将上一代的最优个体保存到下一代种群当中，此时若算法随机初始化中的优良个体保存数量较少，会在很大程度上影响算法的收敛精度和收敛速度。因此本文采用对立学习策略对传统鲨鱼优化算法进行初始化

对立学习策略是由Tizhoosh首次提出，其优点在于算法初始化时，通过产生当前个体以及与其对立的个体，并将当前个体和对立个体进行适应度值对比，筛选适应度值较好的个体作为初始种群个体，很大程度的提高了算法的种群多样性，从而提高了算法的搜索效率。

设在定义域[a,b]内存在实数x，则存在实数x的对立点为x*，x*=a+b-x。因此鲨鱼优化算法随机初始化的对立初始化公式为

(11)

式中，i=1,2,…NP。由此基于对立学习的鲨鱼优化算法初始化步骤如下：

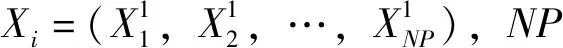
(3)将两个种群合并，并将合并后的 个个体进行适应度值计算，并比较排序，筛选出适应度值最大的NP个个体最为初始化种群。

其次为了避免传统鲨鱼优化算法因早熟收敛陷入局部最优影响寻优精度的问题，本文通过自适应变异策略对算法的全局搜索方式进行改进。目的是当算法陷入局部最优时会对粒子产生扰动力，帮助算法跳出局部最优，提高算法的全局搜索能力和收敛精度。其变异公式为

xi(t)=(1+β)xi(t)

(12)

式中，β为[0,1]之间服从均匀分布的随机数。

具体的改进算法的计算步骤如下所述：

Step1:初始化参数：即鲨鱼种群规模大小NP，最大迭代次数tmax。

Step2:在可行域空间内初始化鲨鱼种群的位置，再利用对立学习策略生成对立种群。

Step3:合并两个种群并计算每一头鲨鱼相应的适应度值，从2NP个个体中选择适应度值较大的NP个个体作为初始种群；

Step4:计算出NP个个体适应度值的大小，找出适应度值最小的个体位置作为最优位置。

Step5:依照式(7)和式(10)对鲨鱼优化算法的速度和位置进行更新。

Step6:依照式(12)对粒子进行均匀变异操作。

Step7:判断是若达到终止条件，是则输出最优个体，即算法找到的最优解；否则，返回Step4。

3 控制算法性能测试

为了验证本文所提改进鲨鱼优化算法的高效性，本文以12个基准测试函数为评价指标，对比本文所提ISSO算法、CPSO算法[6]、改进遗传算法[7]和IBPSO[9]实验所得结果，其中为保证实验公平性，4种算法种群规模均为50，迭代次数均为100，4种算法每个测试函数独立运行50次取平均值和最小值，其中测试函数如表1所示，具体测试结果如表2所示，最优解用加粗字体表示。其中测试函数f1～f4为单峰函数，维数为30，f5～f8为多峰函数，维数为30，f9～f12为固定维函数，维数分别为4,2,2,2。

表1 12个基准测试函数

表2 12个测试函数的测试结果对比

由表2可得，对于单峰测试函数f1～f4而言，本文所提ISSO算法所求解的平均值和最小值相较其他3种算法所求解的平均值和最小值更小，说明ISSO算法具有更高的搜索精度，算法整体性能更加稳定。对于多峰函数f5～f8而言，在其他3种优化算法均陷入局部最优时，仍具有较高的搜索精度。说明本文所提ISSO算法的整体性能要优于其他3种算法。对于固定维函数f9～f12而言，优于测试函数维数整体降低，导致所求问题的复杂度整体降低，因此4种算法的收敛精度均有所提升，但对于测试函数f9和f10而言，本文所提ISSO算法可以取得更小的最小值，因此验证了本文所提ISSO算法的稳定性要更高。整体而言，本文所提ISSO算法具有较高收敛精度和稳定性，算法整体性能较传统SSO优化算法有较大提高，可以用于自抗扰控制器参数整定。

4 基于旋转倒立摆的仿真对比

旋转倒立摆作为一类单输入多输出的强耦合非线性系统，很多控制理论通过以其作为被控对象，验证控制器的控制效果，是验证自动控制理论的重要途径之一，因此本文以旋转倒立摆作为被控对象，验证本文所提改进鲨鱼优化算法的自抗扰控制器的控制效果。其中旋转倒立摆的非线性模型如下所示：

(13)

式中，m1=0.2 kg为旋转杆质量；R1=0.2 m为旋转杆长度；L1=0.1 m为旋转杆到轴心的距离；电机转矩Km=0.0236 n·m/v；f1=0.01 n·m·s为旋转杆绕轴心转动的摩擦力矩系数；旋转杆绕轴心旋转的转动惯量J1=0.004 kg·m2；摆动杆质量为m2=0.52 kg；R2=0.25 m为摆动杆长度；摆动杆到轴心的距离为L2=0.12 m；电机速率为Ke=0.2865 v·s；f2=0.001 n·m·s为摆动杆绕轴心转动的摩擦力矩系数；J2=0.001 kg·m2为摆动杆绕轴心旋转的转动惯量。

本文将ITAE指标作为评价函数，其数学表达式如式(14)所示：

(14)

因此基于改进鲨优化算法自抗扰倒立摆的控制流程图如图2所示。

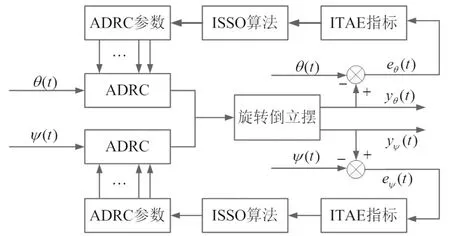
图2 基于改进鲨鱼优化算法的自抗扰旋转倒立摆控制框图

通过ISSO优化后的自抗扰控制参数如表3所示。

表3 自抗扰控制器参数

最后本文以改进鲨鱼优化算法的自抗扰控制器(ISSO-ADRC)对旋转倒立摆进行运行控制，并通过对比改进分数阶PID控制器[3](IMOPSO-FOPID)，传统自抗扰控制器(ADRC)[12]的控制效果，验证本文所提控制策略的有效性。其中摆角和转角的期望输入均为0，目的是当旋转倒立摆起摆后，可以使旋转杆转角和摆动杆摆角的角度均为0。具体实验结果如图3～图6所示。

图3～图4为旋转倒立摆摆角和转角的动态响应曲线，从图中可得，对比IMOPSO-FOPID和传统ADRC的控制效果，本文所提ISSO-ADRC控制误差最小，超调最小且可以更快到达稳态。因此本文所提ISSO-ADRC具有更高的控制精度。

图3 摆动杆摆角响应曲线

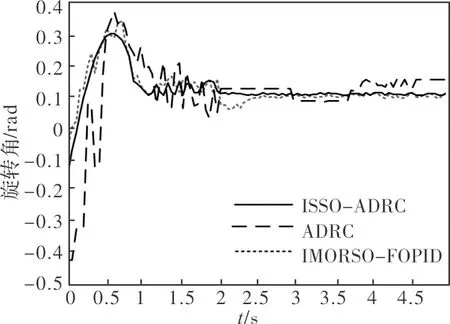
图4 旋转杆转角响应曲线

图5 加入扰动后的摆杆摆角响应曲线

为了验证所提控制算法的有效性，当t=2 s时加入一个幅值为0.1，频率为10 Hz的正弦转矩扰动，从图5～图6中可得，现较其他两种控制方法，本文所提ISSO-ADRC控制策略受扰动影响更小，可以更快对扰动进行观测补偿，使系统尽快稳定。因此，本文所提ISSO-ADRC控制策略的鲁棒性更强，具有较好的抗扰动能力。

5 结 语

本文首先针对传统控制策略难以有效对旋转倒立摆进行位置平衡控制的问题，提出一种自抗扰控制策略。其次针对传统自抗扰控制器由于耦合参数过多难以整定以至于影响控制器精度的问题，提出一种基于改进鲨鱼优化算法的整定方法，并通过对立学习策略和均匀变异对鲨鱼优化算法进行改进，提高了算法的种群多样性和收敛精度，改善了算法的全局收敛能力，并将改进后的鲨鱼优化算法在线整定自抗扰控制器参数。最后以经典的旋转倒立摆为被控对象，通过对比试验，验证了本文所提基于改进鲨鱼优化算法自抗扰控制器具有较高的控制精度和抗扰动能力。