我国股债汇风险点的长记忆性及关联性研究

■潘群星，宦先鹤

本文以2010年6月21日～2019年4月30日期间的上证综合指数、上证国债指数以及人民币兑美元汇率的收益率为样本，基于ARFIMA-HYGARCH模型分别对我国股债汇风险点的长记忆特征进行刻画，并在此基础上构建三元VFIAR-DCC-HYGARCH模型，旨在探究各自间的关联性问题。结论如下：股市收益的长记忆性不显著，而波动存在显著的长记忆特征；债市和汇市的收益与波动存在显著的双长记忆特征；三大风险点间的关联程度均较低，但具有很强的波动时变性，其中股市与债市、债市与汇市表现为正相关关系，股市与汇市表现为负相关关系。基于以上结论，本文为如何有效防范金融风险提出了相应的建议。

一、引言与文献综述

现阶段，我国金融业快速发展，随着实体经济增速下行压力的加大，资金脱实向虚、社会高杠杆等现象愈加明显。加之，受国外宏观政策外溢效应的影响，风险正在金融体系内部以及实体经济运行的多个层面逐渐累积，诸如股指异常波动、债券违约频发、汇率难以稳定等现象仍屡见不鲜。总的来说，国内金融形势良好，金融风险可控，但各金融领域的风险仍处于易发、高发的状态，需要时刻保持高度警惕。股市、债市和汇市作为金融市场的三个主要子市场，它们在社会资源配置、金融风险管理等方面都发挥着重大作用。在当前背景下，对我国股债汇三大风险点的长记忆性及关联性问题进行研究，发掘各市场的典型事实特征，理解市场间的相互作用机制，不论是对投资者把握市场发展形势，构建更加合理的资产组合，还是对监管部门有效进行金融监管和风险控制，制定适当的金融市场调控政策，都具有重要价值。

有关时间序列的长记忆性研究，国外学者构建了许多数学模型。Mandelbrot et al.（1968）基于长记忆现象的研究给出分形高斯噪声的概念，并构建了分数差分噪声（FDN）模型。此后，Granger&Joyeux（1980）、Hosking（1981）将其与自回归移动平均（ARMA）模型联系起来，进一步提出分整自回归移动平均（ARFIMA）模型。之后，Baillie et al.（1996）将分形理论引入GARCH模型，得出分数求和广义自回归条件异方差（FIGARCH）模型。此外，一些学者还尝试将ARFIMA模型分别与FIGARCH和HYGARCH模型结合，构造出ARFIMA-FIGARCH和ARFIMA-HYGARCH模型同时考察时间序列一阶矩和二阶矩上的双长记忆特征。基于上述模型，杨宇俊和门明（2009）指出，银行间国债波动的长记忆性能力强于交易所国债，在估计VaR值时波动过程的长记忆特征是一重要影响因素，基于偏t残差分布所得的HYGARCH模型对中国银行间国债市场的拟合是较为充分的。刘汉等（2015）基于AR-HYGARCH考察了大中华区共4个股市的波动特征，结果表明所有市场收益率均表现出显著的长记忆特征。

有关股债汇风险点间的关联性研究，国内外学者主要围绕股债、股汇和债汇两两风险点展开。有关股债风险点间的关联性，Dean&Faff（2011）利用ABEKK和ADCC-GARCH模型，以澳大利亚1992～2006年间的数据为研究样本，对股票和债券收益率一阶矩上联动效应的非对称特征进行分析，结果表明只有在股市出现好消息和债市出现坏消息时，才会影响对方市场。Nektarios&Charlotte（2012）基于STR模型考察了高频数据下美国股债两市间的关联性，他们认为二者间的相关关系具有时变特征，且正负转换现象明显。从国内研究看，胡秋灵和马丽（2011）采用BEKK-MGARCH模型，分阶段考察了处于不同股市行情特征下股债两市收益率二阶矩上的关联性，结果表明基于不同阶段所得的波动溢出结果各有差异。王雯等（2018）运用DCC-GARCH模型分析了我国股债两市间的动态关联性，最终发现二者间的相关系数具有时变特征，总体关联程度不高但正负方向变化明显。有关股汇风险点间的关联性，Moore et al.（2014）的实证结果表明，在韩国等6个亚洲新兴市场和日本等4个发达市场中，实际汇率与股价间均存在显著的动态关联性。从国内研究看，冷松和田刚（2017）构建了TVP-VAR-SV模型，并将其应用于人民币汇率和利率变动影响我国股价的分析之中，结果表明相关影响具有显著的时变特征，且与利率相比，汇率变动造成的影响更弱。有关债汇风险点间的关联性，So（2001）运用多元EGARCH模型对美国利率和美元汇率的相互作用关系进行分析，发现利率变化会对汇率造成影响，反之则不存在，此外两者还具有波动溢出层面的影响。从国内研究看，陈守东和高艳（2012）通过实证分析指出，从波动层面看，汇率对利率会由金融危机前的单向影响逐渐转变为金融危机后的双向影响。陈创练等（2017）选取TVP-VAR模型对汇改后我国债汇两市月度数据间的动态关系进行了分析，结果表明汇率变动在短期内会对债市产生负向影响，且债市变动在短期内对汇市同样也会产生负向影响，但长期来看影响相对较弱。

经过文献梳理发现，由于选取的样本和采用的方法等各不相同，国内外学者在研究股债汇风险点的长记忆性、关联性问题上并没有得出统一结论，尚存在以下不足：第一，研究维度的不足。在探究不同风险点间的关联性时，大多文献的研究对象仅限于股债汇市场中的某两个，而随着金融市场一体化程度日益深化，单个市场的变化可能影响其他市场，同时也会受到其他市场变化的影响，相较于分割性地研究两两风险点间的关联性，考察多个风险点往往能获取更加丰富的信息，而且能有效降低市场价格内生性对参数估计的影响，使研究结论更为可靠；第二，研究视角的不足。考虑到金融市场受内外部诸多因素影响，且作用机制复杂多变，金融时间序列通常表现出不同程度的长记忆特征，而不同风险点间的关联性既可能与相互间的信息传递有关，又可能与单个市场自身的惯性（即长记忆性）有关，因而要想准确地从信息传递机制层面探究不同风险点间的关联性，就必须去除各自存在的长记忆性成分，但已有文献在探究各风险点间关联性时大多忽略了长记忆特征的影响。鉴于此，本文以我国股债汇三大风险点为考察对象，将其放入到一个统一的分析框架中，并将长记忆性研究和关联性研究相联系时优化研究方法。具体来看，首先基于ARFIMA-HYGARCH模型对各市场均值和波动过程的长记忆特征进行刻画，并在此基础上构建三元VFIAR-DCC-HYGARCH模型探究各自间的动态关联性。

二、研究方法

（一）ARFIMA-HYGARCH模型

为捕捉各风险点条件收益过程的长记忆性，本文选取了分整自回归移动平均（ARFIMA）模型，为捕捉各风险点条件波动过程的长记忆性，一些学者选取分数求和广义自回归条件异方差（FIGARCH）模型，Christian（2010）指出，该模型存在不平稳性（四阶矩的存在问题）、固定振幅限制（通常限定为S=1）等方面的缺陷，可能会影响模型估计的精确性和可靠性。因此，本文将双曲广义自回归条件异方差（HYGARCH）模型与其相结合，构建了能同时考察单个市场收益率序列一阶矩和二阶矩过程长记忆特征的ARFIMA-HYGARCH模型。对于给定的平稳时间序列 rt，ARFIMA（p1，dm，q1）-HYGARCH（p2，dn，q2）模型可表示为：

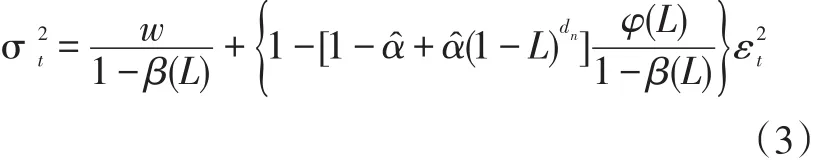
式（1）为模型的条件均值方程。其中，-0.5＜dm＜0.5，μ为样本均值，εt为白噪声序列分别为p1和q1阶滞后算子多项式，且所有根都落在单位圆外，分数差分算子（1-L）dm可通过如下形式展开：

对于记忆参数dm：当-0.5＜dm＜0时，序列为短记忆平稳过程；当0＜dm＜0.5时，序列为长记忆平稳过程；当dm=1时，模型演变为ARIMA模型；当dm=0时，模型演变为ARMA模型。

式（2）为模型的残差或新息分布。其中，et为满足均值为0，方差为1的独立同分布的新生变量。考虑下文的描述性分析结果中各市场收益率均不服从正态分布的原假设，故本文在实证部分将对比t分布、GED分布和偏t分布三种情形进行改进。

（二）三元VFIAR-DCC-HYGARCH模型

为探究不同风险点间的关联性，现有文献多以VAR-MVGARCH模型来结合收益率一阶矩和二阶矩两个层面展开分析。但需指出的是，此类模型并未考虑长记忆特征的影响，通常不同风险点间的关联性既可能与相互间的信息传递有关，又可能与单个风险点的惯性（即长记忆性）有关，要想准确地从信息传递机制层面探究不同风险点间的关联性问题，就必须去除各自存在的长记忆成分。因此，在条件均值部分，本文构建了长记忆VAR（简称VFIAR）模型，该模型以各市场收益率序列分别去除长记忆性后所得的新序列（1-L）drt为研究对象，充分考虑了各收益率一阶矩过程的长记忆特征和各变量及其滞后项间的价格联动关系。在条件方差部分，文章采用了DCC-HYGARCH模型，该模型以VFIAR模型所得的残差序列为研究对象，充分考虑了各收益率二阶矩过程的长记忆特征和各变量间的动态相关关系。最终通过将上述两个部分相结合，构成三元 VFIAR（k）-DCC-HYGARCH（p，d，q）模型。若一个包含三组平稳收益率序列的向量可以表示成rt=（r1，t，r2，t，r3，t）′，r1，t，r2，t和r3，t分别表示我国股债汇市场的收益率，则该模型可表示为：

式（5）为模型的条件均值方程。其中，（1-L）drt为各市场收益率序列经分数差分后所得的新序列组成的向量，具体可分解为为常数向量；对于i≥1，Φi为系数矩阵；εt为残差向量。

式（6）为模型的残差或新息分布。同样考虑下文的描述性分析结果中各市场收益率均不服从正态分布的原假设，因而本文假定该向量服从多元t分布，且在给定过去扰动It-1下条件均值为0，条件协方差矩阵为Ht=（hij，t）3×3，自由度为v。

式（7）为模型的条件方差方程。其中，Dt是由单变量HYGARCH模型所得条件标准差作为对角元素得到的矩阵；Rt=（ρij，t）3×3是条件相关系数矩阵，具体展开式为：

此处，Q=（qij，）t3×3为对称的正定矩阵，则是由该矩阵对角元素平方根作为对角元素所得的矩阵，为μt的无条件协方差矩阵，μt为标准化残差向量且有μt=D-1εt，α和β分别为之前标准化残差平方和条件方差的参数，满足约束：α≥0，β≥0和α+β＜1。有关该模型的估计，本文借鉴蔡瑞胸（2016）使用两步估计法的做法。

三、实证分析

（一）数据及描述性统计

本文分别选取上证综合指数、上证国债指数收盘价以及人民币兑美元汇率中间价（直接标价法）的日交易数据来反映我国股债汇三大风险点的总体情况。考虑央行于2010年6月宣布重启人民币汇率形成机制改革，此后政府干预有所减少，人民币汇率更为贴近市场，能更为有效地反映我国外汇市场的变化情况。因此，本文将研究的样本区间设定为2010年6月21日～2019年4月30日。为保证同步性，剔除因休息日导致的缺失数据和各市场交易日不匹配数据后得到每个变量共2154个观测值。其中，人民币兑美元汇率中间价由外汇管理局系统给出，其余指标由Wind资讯数据库给出。文中有关实证部分所采用的数据分析处理软件主要包括Eviews9.0、Oxmetrics6.2和R语言。

相较于资产价格序列，在其基础上得到的收益率序列往往具备更好的统计特性，且更能有效地反映投资者的获利机会。基于此，本文对各市场的价格数据展开了对数差分变化，得到收益率数据，即：

式中，ri，t为i市场在 t时刻的收益率，pi，t为 i市场在t时刻的收盘价或人民币兑美元汇率中间价，当i取1、2和3时，分别代表股市、债市和汇市。

表1 描述性统计特征

表1为样本期内三个变量的基本统计结果。均值统计量表明股票和债券价格指数存在上升趋势，人民币兑美元汇率略微升值；标准差统计量表明股市收益率的波动最大，汇市次之，债市最小；偏度和峰度统计量体现了各变量存在不同的尖峰厚尾现象，正态性检验的JB统计量进一步显示在1%的水平下所有变量都不服从正态分布，因而后文将在模型中放宽该假设。从序列和平方序列滞后12阶混成检验的LB统计量看，各变量在1%的置信水平下均存在显著的序列自相关性和异方差。单位根检验的ADF统计量表明所有变量都是平稳的。

（二）长记忆性研究

为考察我国股债汇风险点的长记忆性，本文采用ARFIMA-HYGARCH模型分别对各市场收益率序列进行了估计。由于众多的实证结果显示GARCH（1，1）类模型足以刻画金融市场的波动特征，故而令HYGARCH形式中p2和q2的阶数分别对应取1。而有关ARFIMA形式中p1和q1的阶数，本文主要在0≤p1≤3，0≤q1≤3范围内，依据AIC和BIC信息准则、参数结果的显著性、残差诊断等标准进行综合选取。此外，针对各市场收益率序列表现出的尖峰厚尾现象，具体估计时还考虑了模型中新生变量et服从t分布、GED分布和偏t分布的三种情形。经过反复地试算与对比，最终的研究结果表明：对于股票市场，建立GED分布形式下的ARFIMA（0，dm，0）-HYGARCH（1，dn，1）模型结果最优；对债券市场，建立偏 t分布形式下的 ARFIMA（3，dm，0）-HYGARCH（1，dn，1）模型结果最优；对于外汇市场，建 立 偏 t分 布 形 式 下 的 ARFIMA（3，dm，1）-HYGARCH（1，dn，1）模型结果最优。具体结果由表2给出。

从联合估计结果看，除个别参数外，模型中的参数估计值大多在10%的置信水平下通过显著性检验。描述股债汇三市收益率序列长记忆特征的参数dm值分别为0.0082、0.1312和0.1817。其中，仅股市的dm值不显著，而债市和汇市的dm值在5%的置信水平下通过显著性检验，表明股市收益的长记忆性不显著，而债市和汇市的收益存在显著的长记忆特征。描述股债汇三市波动率序列长记忆特征的参数dn值分别为1.0859、0.4126和0.3628。其中，股市和汇市的dn值在1%的置信水平下通过显著性检验，而债市的dn值在10%的置信水平下通过显著性检验，表明股债汇三市波动的长记忆性均是显著的。

从残差诊断结果看，标准化残差的LB统计量（Q（12）、Q（24））和平方标准化残差的LB统计量（Q2（12）、Q2（24））均在5%的置信水平下不显著，12阶和24阶ARCH效应的检验统计量也都不显著，说明各市场收益率序列的自相关性和条件异方差性已被消除。此外，刻画尖峰厚尾特征的GDE分布和偏t分布中所有参数的估计值均在1%的置信水平下通过显著性检验。因此，可以认为基于不同残差分布建立的各市场最优模型的拟合是较为充分的。

表2 ARFIMA-HYGARCH模型估计结果和残差诊断表

总体来看，我国股债汇风险点均存在不同程度的长记忆特征，表明各市场效率较低，无法达到弱式有效水平，历史或突发信息会对单个市场当前和未来的收益与波动产生不同程度的影响。究其原因，一方面，投资者并非是完全理性的。知识、经验、能力等方面的区别可能引发不同的投资行为，且相较于机构投资者，我国金融市场中广泛存在的散户投资者在信息获得方面往往处于劣势，其通常依据自身的主观判断进行决策，同时还会表现出羊群效应等非理性特征，最终使得市场很容易表现出某一趋势持续增强的特点。另一方面，国内金融市场的发展对政府政策具有较强的依赖性，“政策市”特征明显。过多的政策干预会直接影响市场的自我调整，导致市场中的异常波动现象时有发生，特别是重大政策的出台对金融市场造成的影响通常在短期内难以消除。

（三）关联性研究

为进一步探究我国股债汇风险点间的关联性，本文构建了三元VFIAR-DCC-HYGARCH模型。具体估计结果包括条件均值VFIAR（k）模型和条件方差DCC-HYGARCH（p，d，q）模型两部分。为方便论述，下文将分别对这两部分展开分析。

通常在对VFIAR模型进行参数估计前，需先确定其记忆参数d值以及滞后阶数k值。有关d值，由长记忆性研究结果可知，在样本区间内，除股市外其他两个市场的收益均存在显著的长记忆特征。因此，在利用分数差分算子（1-L）d对股债汇三市收益率序列进行差分处理时，可令记忆参数d值分别对应取0、0.1312和0.1817，最终得到对各市场收益率序列 ri，t分别去除长记忆性后的新序列记为 ri，td，经检验三组新序列都是平稳的，故在此基础上建立VFIAR模型是合适的。有关k值，本文基于常用的5种指标进行综合判断。其中，似然比统计量（LR）、最终预测误差（FPE）和赤池信息准则（AIC）显示k值取3时模型达到最优，故本文将k值设定为3，得到VFIAR（3）模型。经检验该模型估计的所有特征根的模均处于单位圆内，可以认为模型是稳定的。同时，由于截距项估计并非关注的重点，以下主要给出各系数矩阵的参数估计结果，如表3所示。

一方面，各市场收益率在不同滞后期的收益值均会对当前自身的收益率造成影响，序列自相关性明显。具体来看，股市收益率受到了其滞后1期收益值的正向影响，债市收益率受到了其滞后1、2和3期收益值的负向影响，汇市收益率受到了其滞后1和2期收益值的负向影响。另一方面，各市场收益率间存在着交叉滞后的影响，价格联动效应明显。股市收益率方程中，汇市滞后1期的收益值在10%的置信水平下对其有正向影响。债市收益率方程中，汇市滞后2期的收益值在10%的置信水平下对其有负向影响。汇市收益率方程中，债市滞后2和3期的收益值在5%的置信水平下对其有正向影响。

表3 VFIAR（3）模型估计结果

考虑上述模型中存在着一些不显著的估计参数，在5%的置信水平下，本文对其进行简化后得到一个新模型，称为简化的VFIAR（3）模型。经检验该模型的AIC和BIC信息准则值均有所下降，且残差的自相关性也已被消除，但仍具有较强的ARCH效应。因此，基于简化的VFIAR（3）模型所得的残差序列，可进一步估计DCC-HYGARCH模型。限于篇幅，此处直接给出了模型中一些重要参数的估计结果，其中α=0.0031且在5%的置信水平下显著，β=0.9943且在1%的置信水平下显著，满足α+β＜1的约束条件，说明各市场间的动态相关系数受过去随机扰动的影响较弱，而受过去相关系数的影响较强，表现出波动持续性特征。

为了更加清晰和直观地体现中国股债汇风险点间动态相关系数的变化情况，图1分别列出了三者两两之间相关系数的时序图。可以看出：第一，其变动范围均介于-0.13～0.11之间，表明各市场间总体关联程度均较低，存在一定的市场分割；第二，其随时间变化而发生显著变动，时变特征明显，具体来看，除个别时间段外，股市与债市、债市与汇市表现为正相关关系，股市与汇市表现为负相关关系，表明无论是不同时段两市场间的关联性，还是总体时段不同市场间的关联性均存在差异；第三，其变动幅度较为频繁，且存在逐渐扩大趋势，特别是在股灾、811汇改等重大事件发生期间的大幅变动现象尤为明显，表明单个市场对于其他市场的变动较为敏感，风险会在不同市场间进行传播。

图1 动态相关系数图

综上所述，我国股债汇风险点间的关联程度均较低但具有很强的波动时变性。其中，股市与债市、债市与汇市表现为正相关关系，股市与汇市表现为负相关关系。表明我国金融市场的一体化程度较低，信息传导不够畅通，存在一定的市场分割。但是，不同时段各市场间的关联性仍存在差异，单个市场对于其他市场的变动较为敏感，风险会在不同市场间扩散。究其原因，第一，各市场的投资主体不同，不同的投资主体往往使得各市场的内在运行机理无法统一。第二，金融产品较少且联系不紧密。我国的新金融产品的出现并非市场发展的结果，其更多地会受监管部门等多方面的制约。第三，各市场的监管和政策主体不同。我国国内政府通常会参与到相关市场的调节和引导过程中，不同市场涉及的相关部门往往会在满足自身利益条件下制定相应的政策制度。

四、结论与建议

本文基于ARFIMA-HYGARCH模型考察了我国股债汇三大风险点的长记忆特征，并在此基础上构建VFIAR-DCC-HYGARCH模型进一步探究了各市场间的关联性问题。研究结论显示：在样本区间内，股市收益的长记忆性不显著，而波动存在显著的长记忆特征。债市和汇市的收益与波动存在显著的双长记忆特征；各风险点间的关联程度均较低但具有很强的波动时变性，其中股市与债市、债市与汇市表现为正相关关系，股市与汇市表现为负相关关系。为此，结合金融风险防范的目标，本文给出如下建议：

从记忆性研究结果看，我国金融市场效率较低，无法达到弱式有效水平，历史或突发信息会对金融市场当前和未来的收益与波动产生不同程度的影响。因此，对于投资者而言，在其进行资产预测和风险度量时要将相关市场的历史信息充分考虑在内，避免自身行为的随意性；对于政府部门而言，要明确其在金融市场中的职能定位，有效区分政府和市场行为，减少政府对市场的功能替代，使金融资产价格能准确反映市场的供求状况；对于监管部门而言，要加快信息披露机制的构建，保证市场信息及时公开和准确有效，减少不对称现象以及内幕交易行为。同时还要注重中小投资者的利益，进一步发展机构投资者，在逐渐提高各市场参与者分析水平的过程中引导其树立正确的投资理念。

从关联性研究结果看，一方面，我国金融市场的一体化程度较低，信息传导不够畅通，存在一定的市场分割。因此，要不断加强各市场间的联通，在深入推进股票、债券等资本市场对外开放以及人民币汇率形成机制改革的同时逐步放松对资金流、投资主体等方面的管制，并通过金融创新来丰富各市场中的交易产品种类，吸引更多具有不同风险偏好和风险承受能力的市场参与者，依靠其跨市场交易活动促进市场间的信息传递。另一方面，不同时段各市场间的关联性存在差异，单个市场对于其他市场的变动较为敏感，风险会在不同市场间扩散。因此，首先要密切关注各市场间关联性的变化情况，发掘其中的有效信息，并以此做好有关跨市场资产配置、市场调节政策等的变更。其次可形成相应的预警指标，一旦其发生异常变动，能及时启动应急机制对目标风险点以及与其存在明显关联性的其他风险点进行处置，避免风险扩散。最后要强化多个部门间的沟通合作，逐步提升监管政策的针对性、有效性，以实现各类市场的协调发展。