中美金融波动的协动性及风险传导路径分析

■郭 畅，苏 鹏，姜晓春

本文首先通过SVAR模型构建了中美两国金融状况指数来表征金融波动，其次用马尔可夫区制转换模型将其划分为繁荣和萧条两种状态，由此构建了反映两国金融波动同步性的协动指数（SI），最后用因子分析和门限回归分析了两国金融风险的传导路径。研究表明，中美金融波动周期长度接近，但呈现出截然不同的非对称特征。中美金融波动协动性及其风险传导路径会随着外部冲击和内部矛盾情势的变化而变化。门限回归结果显示，贸易因子在各区制内均显著，是两国金融联系的基础。金融协动性较低时，汇率因子是金融风险传导的主要途径。随着协动性提高进入中等水平，资产和利率因子成为主导。当协动性到达高区制时，股票和房价等资产因子仍是两国金融联系和风险传导的主通道，但与调控政策相关的汇率和利率因子开始显现出对风险的抵御作用，相关政策协调有助于抑制风险传导。

一、问题的提出

随着经济全球化与金融一体化的不断深入，国家间在实体经济和金融状况上的联系显著增强。尤其是在2007年美国次贷危机爆发后，金融风险迅速地在各国金融市场间传导，致使全球经济衰退。中国是经济增长速度最快的发展中国家，美国是经济体量最大的发达国家，两国对全球金融、经济发展的重要作用不言而喻。因此，研究中美两国金融波动特征及其协动机制，不仅可为中国金融体系改革和发展提供有益的实证证据和政策含义，而且对维护全球金融稳定和经济可持续发展也有着重要参考价值。

金融波动通常区分为中长期低频波动成分和短期高频波动成分。金融波动的中低频波动特征主要集中在房地产价格或信贷的波动上，其波长和幅度通常大于传统经济周期。金融波动中的高频波动则主要涉及股票价格、货币供给、利率和汇率等变量，对其测度则多使用统计方法从多个指标中加权合成或者提取共同成分，构建金融状况指数（FCI）来识别整体金融周期的波动，得到的金融周期长度与宏观经济周期基本一致甚至更短。金融波动的高频波动性部分及时地反映了其与宏观经济间的相互作用，不仅揭示金融市场在内外各种冲击下的波动性，也能反映货币政策及其他调控政策对金融环境的动态回应。考虑到本文的研究目的是分析中美之间金融波动的协同性，本文选择类似高频因素合成FCI的思路，但同时考虑高低频波动成分。

近年来，国内外学者通常选取综合多种金融指标提炼FCI的方法来衡量整体金融状况，主要分为两种计算方法：从多种金融指标中提取共同部分或对金融指标进行加权组合。前者主要使用主成分分析、因子分析和动态因子模型从多个金融指标中提取FCI指数。Brave&Butters（2011）基于大量的美国金融指标使用主成分分析提取出FCI，发现其对政策制定及金融市场评估是一个较好的参考依据。Matheson（2012）使用动态因子模型也成功合成了美国和欧盟的FCI。这种方法的优点在于它综合了较多的金融指标，且不受特定理论假设的限制，但是忽略了金融指标与宏观经济目标间的关联性。因此，学者们更倾向于根据金融变量和宏观经济目标变量（如经济增长或通货膨胀）之间的关系来确定权重，并通过使用多个金融指标的加权组合来计算FCI，确定金融指标权重的方法大致有三种：一是使用大规模宏观经济模拟模型中的系数估计值作为金融指标权重确定的基础（Dudley&Hatzius，2000）；二是根据简化的总需求方程中每个金融变量系数的估计值来确定权重（Montagnoli et al.，2004）；三是借助向量自回归（VAR）模型的脉冲响应分析，计算目标变量（如通胀率）对各个金融变量冲击的累积响应获得权重（Swiston，2008），这种方法不仅可以确保较广的金融指标覆盖范围，而且还具有易于计算、不依赖于经济理论假设等优势，得到了广泛使用。本文将选用第三种方法来计算FCI，由于变量之间存在同期相关性，故而选择结构向量自回归模型（SVAR）的脉冲函数来确定金融变量权重。

基于FCI分析不同国家的金融形势，国内外学者虽进行了广泛深入的研究，但因构建FCI时选取的金融指标和方法上的差异，一定程度上阻碍了对各国金融关联性的比较分析。现有的国际金融关系，尤其是对中美两国金融关联性的分析，均局限于对单个金融市场或指标的具体孤立分析。本文拟选择房地产价格、信贷、股票价格、货币供应量、利率和汇率等六个金融指标来构建中国和美国的金融状况指数，分析两国金融周期的波动特征和协动性，并进一步探讨不同协动性水平下金融风险的传导路径。

二、研究方法

（一）金融变量数据说明及处理

本文遵循两个原则筛选计算FCI的金融变量。一是选用的金融变量在货币政策传导中应具有重要作用；二是选取包含预测未来经济运行状况关键信息的金融变量。根据这些原则，并参考朱太辉和黄海晶（2018）的金融变量选择，本文构建FCI的金融变量包括货币供应量（MS）、利率（IR）、信用贷款规模（CL）、汇率（ER）、股价（SP）和房价（HP）。

本文使用1996年1月～2018年12月共计276个月度的数据，如无特殊说明，本文的数据均取自中经网数据库。用于描述中国金融市场的指标包括广义货币供应量、银行间7天期拆借加权平均利率、金融机构贷款总额、有效汇率、上海证券综合指数和全国平均房价；用于描述美国金融市场的指标包括广义货币供应量、联邦基金实际利率、总消费者信贷、有效汇率、纽约证券交易所综合指数和房价指数。其中，全国平均房价通过全国住宅销售额除以销售面积来得到，汇率数据采用国际清算银行（BIS）官方网站公布的实际有效汇率，美国消费者信贷总额来自美联储网站。中美两国的所有变量都使用各自的消费者价格指数（CPI）进行了换算，CPI均以“2010年月平均价格=100”为基准。首先，在使用的六个金融变量中，利率和有效汇率是反向指标，而其他四个指标通常与金融宽松状况方向相同，故而将这两个指标转换为正指标。利率通过公式ρt=1/（1+rt）转换为当期的贴现率，而有效汇率则通过取倒数，由原来的间接标价转换为直接标价的形式。其次，通过X-12-ARIMA程序对数据进行季节性调整，并且使用Hodrick-Prescott（HP）滤波分解出各变量的循环成分。循环分量实际上是实际值偏离长期潜在趋势值的差额，也被称为缺口序列。最后，标准化所有缺口序列，以消除变量间量纲和波动上的差异。最终得到的标准化缺口序列用Gapi（i=1，…，6）来表示，对应的金融序列如表1所示。

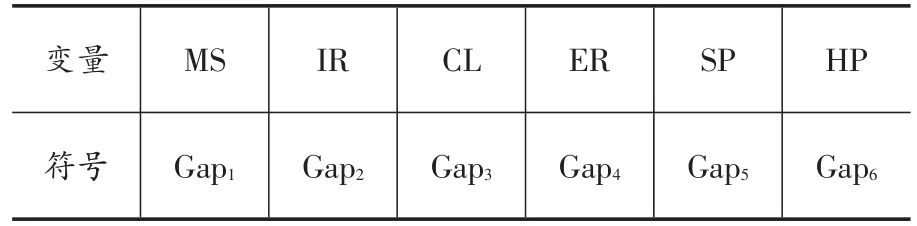
表1 金融缺口序列的表征符号对照

（二）计量方法

1.FCI构建方法

用来测度金融周期的FCI构建公式为：

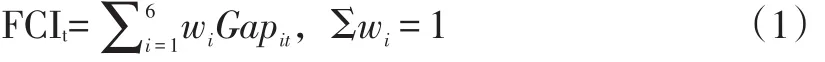
其中，Gapit为对应国家第i个金融变量的标准化缺口序列，wi是其对应的权重。本文FCI反映了一个国家的金融现状与均衡状态的偏差。具体来讲，如果FCI越接近于0，意味着金融状况处于一个接近均衡的适度状态；如果FCI大于0（或者小于0），表示金融状况相对繁荣（或萧条）；如果FCI上升（或下降），说明金融状况在趋好（或恶化）。

计算FCI的关键是确定权重wi，一个成熟的方法是用VAR模型的脉冲函数，计算GDP或通胀等宏观经济目标变量对各金融序列的累积脉冲响应系数来获得。相较而言，SVAR模型不仅保留了VAR变量内生的假设，而且还考虑了变量当期相关性，所以用来计算权重要比VAR更稳健（徐国祥和郑雯，2013）。另外，表征经济增长的GDP数据仅有季度数据，无法与本文使用的月度数据保持一致，且FCI一般是经济增长的先行指标，与通胀率更加一致（邓创和徐曼，2018）。故本文将通货膨胀率πt作为目标变量，与前文所述的6个金融序列组成7元SVAR模型。p阶SVAR模型可表示如下：

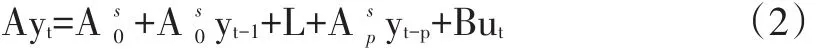
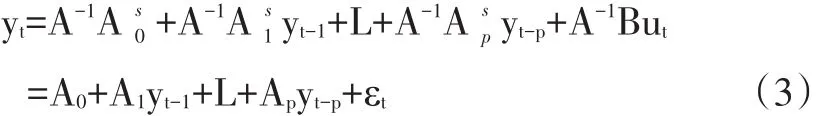
并且，式（2）和式（3）对应的误差结构关系一般设定为

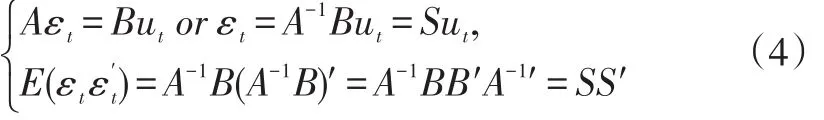
为了从简化模型的参数估计中获得对应的唯一确定的结构参数估计值，需解决识别性问题，主要是通过对参数施加约束的方式实施。基于已有经济理论，约束一般采取长期形式。模型（3）对应的长期约束模型形式如下：

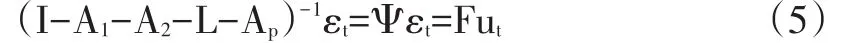
其中，Ψ=1/（I-A1-A2-…-Ap）是长期乘数，可通过简化VAR模型参数估计值得到，且容易看出F=ΨS。对矩阵F施加的约束便是长期识别条件，一般设定某一元素为0。若第i个变量对第j个变量的结构冲击的累积反应在长期是0，则用约束fij=0来表示。考虑到约束的经济含义，本文选择F型SVAR模型来确定FCI的变量权重wi，即对SVAR模型施加长期约束来达到识别条件。根据识别原则，k个变量的情况下，要对矩阵F至少施加k（k-1）/2个约束。本文有7个变量，所以应施加21个长期约束。

常见的设定是把F设定为下三角矩阵，此时变量的排列次序影响着约束的经济含义，所以变量次序很重要。本文标准化后的金融缺口序列均是剔除了价格影响的实际变量，长期中通胀对这些变量无影响。但是本文以通胀率为计算累积脉冲反应的目标变量，需要设定6个对通胀有长期影响的金融变量。因此，把通胀率πt排在第七位置。另外，一般认为政策性变量受其他金融变量影响要小，而其对其他金融变量的影响则较大，所以把货币供给量和利率两个政策性变量放第一和第二位。对于其他变量，则按照各变量的政策倾向性大小降序排列，依次为社会信贷总额、汇率、股票价格和房价。在实际估计中，仍将基于根据矩阵F中各元素的估计结果予以调整。元素fij若不显著，则将其设定为0，同时令其对角元素fji不等于0。依次逐个变量调整，最终得到的中美两国的长期约束矩阵F如式（6）和式（7）所示。

基于上述SVAR模型估计结果，可以得到通胀率对各金融序列的长期累积效应。短期经济周期一般为3～5年，所以本文选择60个月的累积脉冲反应值。最后FCI中第i个变量的权重wi可由下式计算得到：

其中，zi是通胀率对第i个金融缺口序列的累积广义脉冲响应值。至此，再结合等式（1），可以完成FCI的计算。

2.协动性的测度方法

测度中美金融波动的协动性，需先完成对两国金融波动的阶段划分。为避免主观设定引起的偏差，本文选择马尔科夫区制转换（MRS）模型来分析金融周期的波动特征，该方法的转折点完全由数据内生确定。

假设存在繁荣和萧条两个潜在状态，用区制变量st表示，st=1表示繁荣，st=2表示萧条。尽管该概率可设定为时变的，但分析周期时一般设定为常概率。将从t-1期的状态i到t期转换为区制j的转换概率pij表示为

易知p11+p12=1，p21+p22=1。一般地，根据逻辑分布对这些概率进行参数化

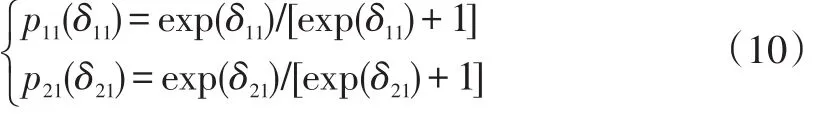
其中，δij决定区制概率的参数，且满足识别标准化δ12=0、δ22=0。那么，均值随区制变化的MRS模型构建如下：

其中，εt～N（0，δ）。模型（11）使用Eviews10.0软件中的转换回归算法完成估计，并可得到转换概率对应的滤波预测值P（st=1|ℑt）和 P（st=2|ℑt），此处ℑt是t期的信息全集。定义状态识别指数如下：

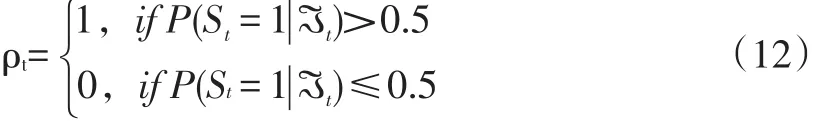
最后，参考Harding&Pagan（2002；2006）的方法，构建一个协动性指数（synergy index，SI）来测度中美金融波动的协动性。不同的是本文在T期滚动地计算该指数，此处的T表示前面MRS模型估计得到的平均周期长度。具体的指数计算公式如下：

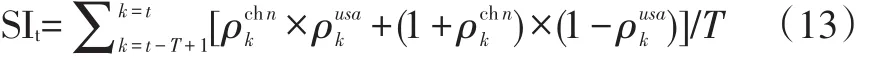
其实，指数SIt度量的是在一个完整周期内中美两国金融周期处于同一状态（繁荣或萧条）的时期比重。显然SIt大于0且小于1，其越接近于1，两国金融周期的协动性便越强。

3.传导路径的分析方法

为了识别对中美金融周期协动性的影响因素，仍需对选取的数据进行一定的处理。具体步骤为：首先在计算FCI时使用的6个金融变量中，考虑到国内信贷总额在外部市场上影响有限，所以予以舍弃。然后计算剩余5个变量的固定T期的滚动相关系数来表征两国房地产市场、股票市场、汇率以及货币政策（货币供给和利率）间的关联。另外，两国贸易的关联度由中美双边贸易总额的T期移动平均增长率（TR）来代理。相应地，该部分的因变量选取两国FCI的T期滚动相关系数。

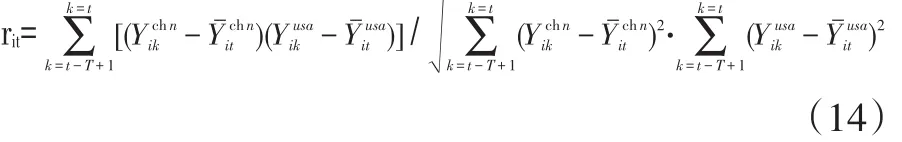
由于多个自变量间存在较强的相关性，本文将使用因子分析进行降维，并从6个自变量中提炼出几个有明确经济含义的公因子。假设存在m个公因子，用fi，i=1，2，…，m表示，那么单个变量形式的因子模型为

其中，lij为第i个变量在第j个因子上的载荷，所有载荷组成载荷矩阵L。进一步令 Rt=（rMSt，rIRt，rERt，rSPt，rHPt，rTRt）′、Ft=（f1t，f2t，fmt）′和vt=（vMSt，vIRt，vERt，vSPt，vHPt，vTRt）′，则式（15）可表达为如下的矩阵形式

为进一步明确公因子的经济学含义，可对载荷矩阵L进行多次正交旋转。假设m维的正交矩阵为H，则旋转后的载荷矩阵L*=LH。本文使用最大方差旋转法来得到L*，而后基于回归方法来获得公因子的预测值，即

其中，Ψ是样本相关矩阵。同时，金融风险的传导路径可能会随着中美两国的金融周期协动性水平的不同而发生变化，进而规避风险的措施也会有所差异，所以用门限回归模型这一非线性模型来分析金融风险的传导路径，门限变量选用SI。以双门限为例，用 V1和 V2表示阈值，且 V1＜V2，则模型设定如下：

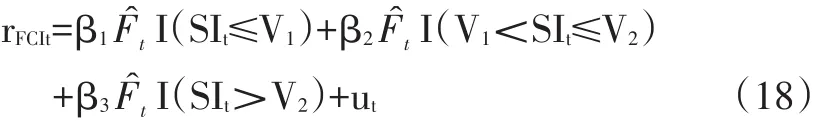
其中，I（∙）是示性函数，当其括号内的事件为真时，取值为1。

三、金融波动及其协动性测度

（一）FCI计算结果及分析

SVAR模型要求平稳序列，ADF单位根检验结果显示所有的缺口序列均在1%水平下显著平稳。另外，基于似然比（LR）、赤池信息准则（AIC）等五种选择标准的结果，将SVAR模型的滞后阶数设定为5。而后基于式（6）和式（7）两个长期约束矩阵的估计结果①限于文章篇幅，对时间序列平稳性检验、SVAR模型滞后阶数的确定和此处的两个长期约束矩阵的估计结果予以省略，读者如有需要可向作者索要。，选用脉冲分析中的结构分解方法，来计算通胀率对每个金融缺口序列的1单位标准差冲击的60期累积反应，结果见图1。根据式（8）计算得到的各序列的权重结果见表2。最后图2给出了中国和美国的FCI计算结果。

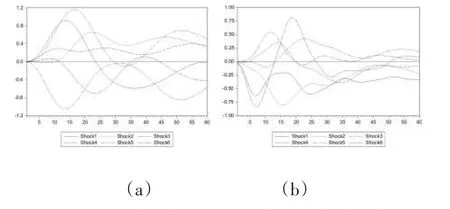
图1 通胀率对各金融序列的累积脉冲反应（a）中国；（b）美国

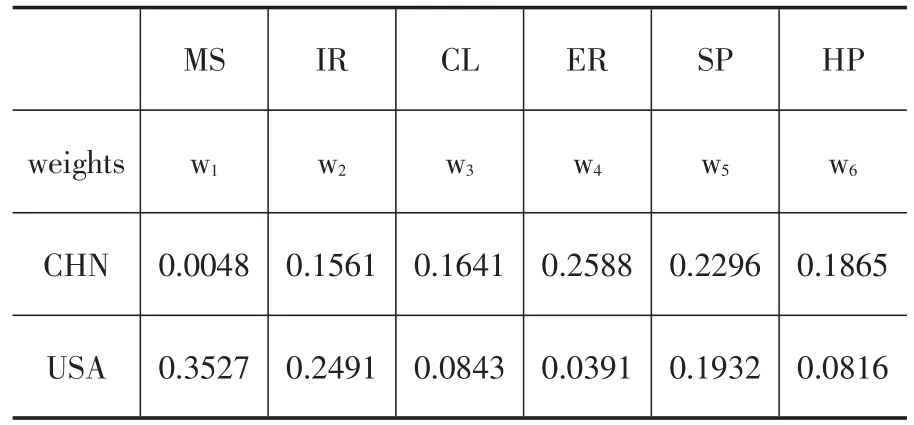
表2 FCI中各金融序列的权重

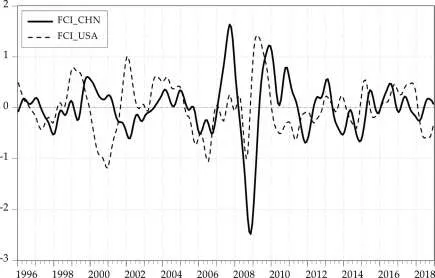
图2 中国和美国的FCI结果

由图2可知，1996～1997年受国内需求不足和亚洲金融风暴影响，中国的金融状况持续恶化。在中国实施了一系列扩张性政策和改革措施后，FCI在1998年开始止跌上升。但随着政策效用的逐步消退，2000年中国FCI开始回落，2001年上半年到达零线。2001年下半年到2003年，中国股市持续低迷，企业融资困难，FCI值始终低于零，金融环境趋紧。2003年下半年，股权改革激发金融市场活力，金融环境向好。为防范经济过热带来的潜在风险，中国采取了一系列旨在控制投资过热的措施，随着监管力度的增加，2005年金融状况不断收紧，并持续到2006年底。2007年，受奥运会刺激，中国经济有所改善，股市、房地产市场等蓬勃发展，中国FCI迅速上升。但2007年底美国金融危机波及中国，FCI迅速下滑，2008年底跌至谷底。为应对金融危机，中国政府及时推出了一揽子刺激政策，2009年FCI迅速有了反弹。受2010年欧洲债务危机影响，中国金融状况再次大幅下滑。2012年中国经济增长于14年来首次降至8%以下，从此步入中低速增长期。以此为契机，中国政府加快金融改革，FCI在2012年得到短暂改善。由于全球经济衰退和自身内部经济结构问题，FCI在2013年开始再次下滑，并于2013年下半年到2015年上半年陷入萧条。随着经济的逐步复苏，政府倾向维稳的调控策略，2015年之后中国FCI稳定于适度偏紧的波动范围。

对于美国，1996年上半年，其银行业由于信贷泛滥而陷入严重的危机，FCI不断下滑。随着信贷质量得以改善，FCI于1997年初开始回升。但亚洲金融危机爆发后并迅速蔓延，全球金融市场陷入混乱。加上受2000年IT泡沫破灭等多个不利因素的叠加冲击，美国金融状况从1998年底开始下行，并长期低迷。为刺激经济，在2001年1月～2003年6月期间美联储13次降息，促使美国金融市场极度活跃，也致使房地产市场集聚了大量资金，房地产泡沫不断膨胀，FCI不断攀高。但2007年美国次贷危机爆发，FCI随之迅速跌入谷底。面对危机，美国政府迅速出台了一系列的救市法案，其金融形势于2010年开始恢复至适度宽松的区间波动。随后受到欧债危机和全球经济形势恶化的影响，美国金融也经历了一段低迷。随着美国经济的逐步复苏，2013年以后金融状况恢复到温和的整体向好态势。由上分析可知，中美两国FCI计算结果具有合理性。

（二）中美金融波动的协动性分析

本节首先使用MSR模型，根据先前计算的FCI对中美两国金融波动状态进行识别与划分，然后根据公式（12）和（13）计算协动性指数SI。表3给出了对中美金融波动特征的MRS模型的估计结果。由估计结果可知，中国和美国均在1%显著水平下存在繁荣和萧条两个状态，且两个状态的维持概率都很高，均显示出较为稳定的特性。并且中美金融周期存在截然不同的非对称特征，中国的繁荣和萧条的平均持续时间分别为28.4和12.7个月，即“长繁荣短萧条”，而美国两个区制则分别为13.3和25.1个月，即“短繁荣长萧条”，造成这一差异的原因可能与两国宏观调控政策效果以及金融市场的完善程度有关。

进一步计算两国FCI的滤波区制概率①区制概率图如有需要，可向作者索要。，根据式（12）对金融波动的两个状态进行识别，则由式（13）可得两国金融波动协动性指数SI。由于美国一个周期38个月小于中国的41个月，所以计算SI时选用的循环窗口T=38，结果见图3。图3中也给出了由式（14）计算得到的38期滚动相关系数作为参照，两者的走势基本上是一致的。

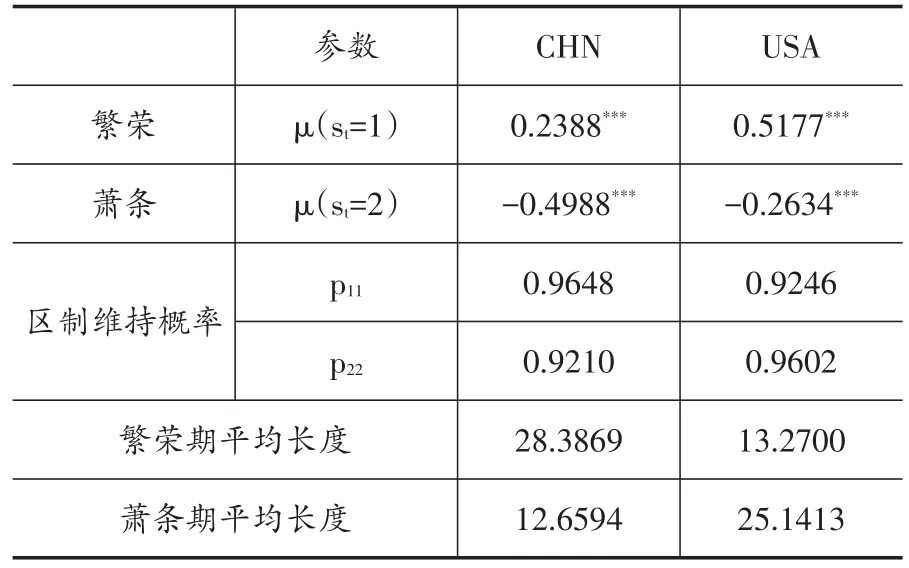
表3 中美金融波动特征的MSR模型估计结果

图3 金融周期的协动性指数及其滚动相关系数

图3 显示，自20世纪90年代中期以来，两国金融波动的协动性不断加强。特别是在亚洲金融危机期间，两国金融波动协动性显著增强。但是随着中美贸易赤字的持续扩大以及两国经济体制等差异，逐步加剧了两国在双边投资上的失衡：表现为美国对华以股票为主而中国对美以债券为主，所以2000～2002年间，两国金融之间的联动程度较小，甚至发生了相互背离的脱钩现象。此后，由于2009年危机期间政策选择上的趋同性，两国金融波动的协动性急剧上升并达到最大值。危机后对美国出口的急剧下降，并意识到美元陷阱的严重性，中国政府开始追求外汇储备多元化，逐步降低对美国金融市场的依赖。因此，2009～2011年两国金融波动基本处于相互独立的状态。2012年以后，随着美国经济复苏，中国经济进入适度增长调整期，两国金融波动的协动性基本保持在0.6左右的稳定期。综上所述，中美之间金融波动的协动性具有明显的时变特征，既有应对危机时的高度协作，也有双方利益博弈时的相互背离。

四、传导路径分析

根据等式（15）和（16），对代表两国贸易，资产市场和政策之间相互关系的6个指标进行因子分析。根据特征值大于1的标准，所选因子数量为m=4。负载矩阵L的估计结果见表4。根据方差最大化原理正交旋转，旋转后的载荷矩阵L*的结果也在表4中示出。

由结果可知，4个公因子对原始变量方差的累积贡献率为1，表明通过因子分析将6个变量简化为四维的过程较为完全。根据每个公因子的旋转载荷，表征两国贸易关联的rTR在因子f1上有最大载荷，本文将其称为“贸易因子”。股价和房价相关性在因子f2上的贡献相对较大，所以将其定义为“资产因子”。依据相同的定义原则，分别将f3和f4定义为“汇率因子”和“利率因子”。在获得稳定因子旋转结果之后，可以根据式（17）计算因子得分序列，可表征每个公因子的波动。将获得的4个因子用作解释变量，以协动性指数SI为门限变量，进行滚动相关系数rFCI的门限回归。

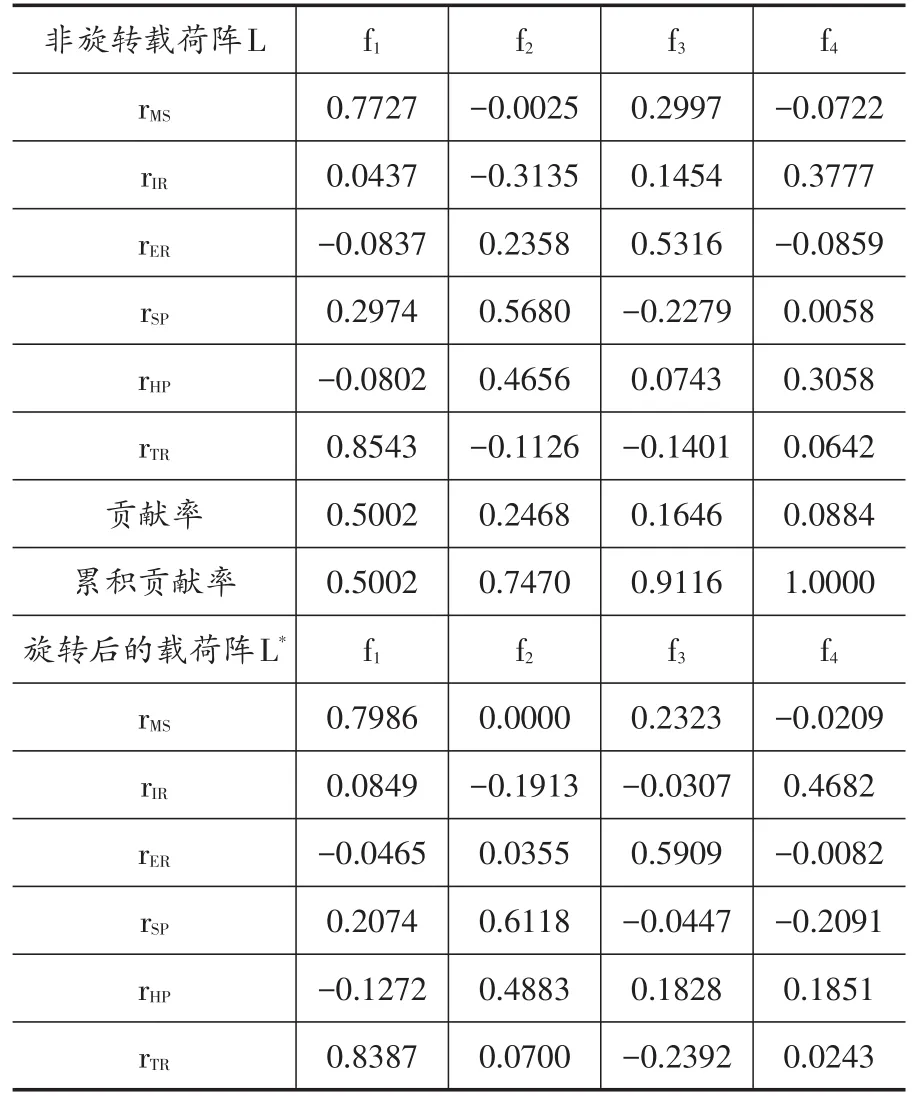
表4 因子分析载荷矩阵估计结果

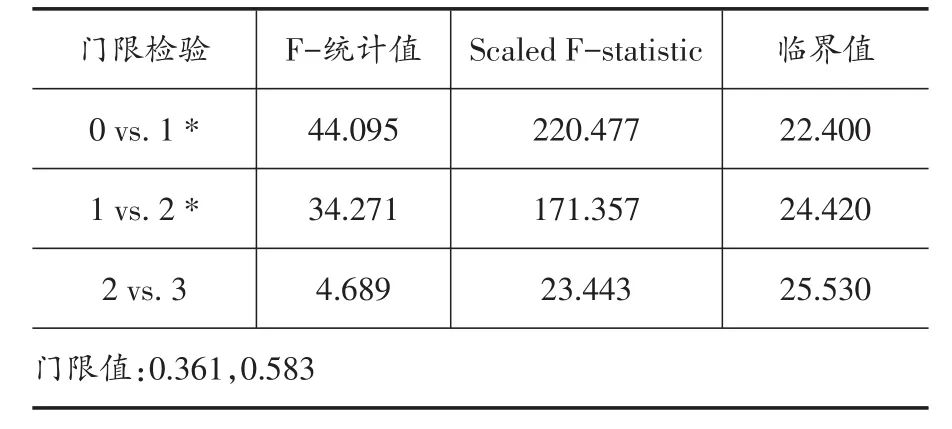
表5 门限值检验

表5的门限检验结果显示，在1%的显著性水平下存在0.361和0.583两个门限值。根据表6中的门限回归结果，当协动性处于较低水平（即小于0.361）时，双边贸易的增长和汇率的相关性增强是中美金融联动的主要原因。随着协同性水平的提高，当处于中等水平（即在0.361和0.583之间）时，除两国之间的贸易增长外，两国在股票、房地产市场以及利率决策上的关联性变得重要起来。当协动性水平达到高水平（即大于0.583）时，4个因子都会导致两国之间金融波动协动性的变化，但2个与政策相关的汇率因子和利率因子是负的影响。因此，在不同的金融波动协动水平下，导致其变化的主要因素存在差异。

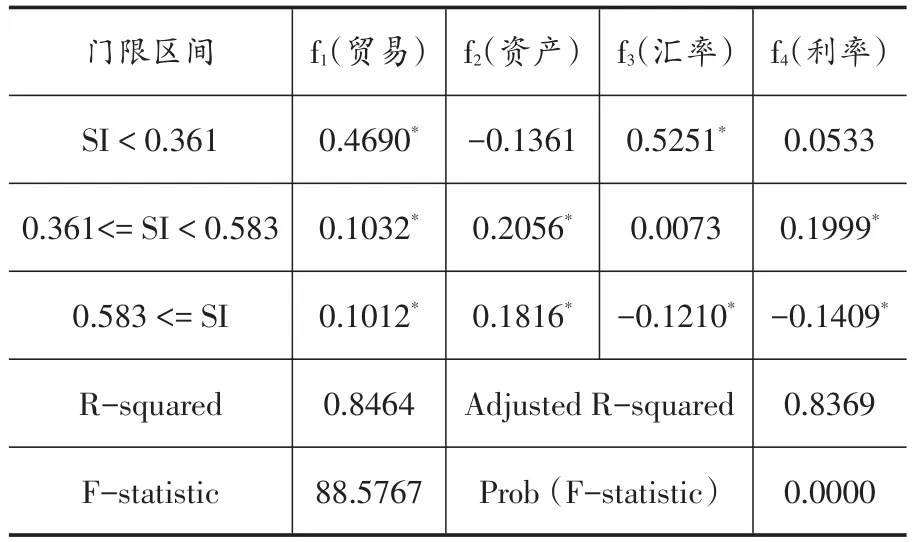
表6 门限回归估计结果

上述结果证实，保持双边贸易的畅通和加强是金融波动联动的基础，因为贸易因子系数在每个门限区间内都是显著的。同时，意味着随着中美宏观经济和金融市场联系的变化，金融风险传导渠道发生了一些重要变化。当两国之间的金融联系较差时，随着两国贸易的不断加强，外汇市场更为重要，汇率渠道成为金融冲击和风险传导的主要路径。但是随着两国在经济和金融活动方面关联性的不断增强，以股价和房价为代表的资产价格联动成为金融周期协动运行的主要驱动因素，资本市场成为国际金融风险传导的主要渠道。此外，利率因子在中等水平时也呈正向影响，一方面意味着利用贸易积累的外汇购买与利率相关的外国债券在两国金融联系中的作用加大。另一方面也意味当协动程度处于中等水平时，应对全球金融危机或经济衰退时采取利率相关的政策协调的需求较低。当中美金融波动表现出高度协动性时，主要是在两次金融危机期间，此时贸易和资产因子仍然是联系两国金融的主要路径。然而为了应对危机的影响，货币供应量、汇率、利率等能够代表货币政策协调的汇率因子和利率因子呈现出抑制作用，会使两国的金融周期相互脱离，避免风险蔓延，此时政策协调需求上升。

五、结论

本文选取6个金融指标，用SVAR模型计算权重，综合得到中美两国各自的金融状况指数。马尔科夫区制转换模型的金融波动状态划分结果表明两国的金融周期分别为41个月和38个月，但各自周期内的特征呈现出截然不同的非对称性。基于两国周期长度，此构建了衡量中美金融波动协动性的协动指数（SI），发现两国金融波动的协动性会随着外部冲击和内部矛盾情势的变化而变化。特别是在两次金融危机期间，中美两国的金融周期表现出高度的协动性。在关于中美金融波动协动性及其风险传导路径的分析中，为避免共线性使用因子分析法较完全地提炼出贸易、资产、汇率和利率4个公因子。对传导路径的门限回归结果显示，协动性指数SI存在0.361和0.583两个门限。整体看，贸易因子是金融波动协动性的基础。当协动性处于较低水平（SI＜0.361）时，汇率因子是导致金融联动的主要原因，也是国际金融风险传导的主要渠道。随着协动性的增强（0.361＜=SI＜0.583），资产因子和利率因子开始成为协动变化的主要原因。当协同效应水平突破0.583时，以股票价格和房价为基础的资本因子仍是两国金融市场联动和风险传导的主要路径，但两国货币政策的协作有利于抵御风险传导。

综上所述，中国应加强对自身金融波动及其主要贸易伙伴的相关监测，以便及时、正确地应对外部风险。如果与风险输出国关联度较低，应该主要关注外汇市场风险。当两国金融波动协动性达到较高水平，应重点监察双方资本市场的波动，适当建立一定的隔离机制，避免风险扩散。同时，积极与其他国家在宏观调控政策上协调合作，共同抵御金融冲击对实体经济的传导影响。