带有输入死区和输出受限的非线性系统自适应控制
曾 文,李志刚,高 闯,陈雪波
(辽宁科技大学 电子与信息工程学院, 辽宁 鞍山 114051)
智能控制领域的自适应控制已成为研究热点,取得了不少科研成果[1-6].通常采用神经网络或模糊控制设计控制器,文献[4]采用模糊控制逼近系统的未知非线性项,文献[5]采用神经网络及backstepping方法设计控制器.
死区广泛存在于实际控制系统,严重干扰了系统的稳定性,限制了系统的性能.文献[7]通过中值定理将死区分解为线性和非线性两个区域.文献[8]基于径向基函数神经网络(radial basis function,简称RBF)和中值定理,对带有死区的纯反馈系统提出控制策略.文献[9]利用模糊逻辑控制替代RBF神经网络,对一类非线性系统设计自适应控制器.文献[10]对一类非线性切换系统的跟踪控制进行了研究.
以上研究均没有对系统输出进行约束,不加约束的工业系统的产能不高,因此设计控制器时就要考虑约束条件的限制[11-14].文献[12]基于障碍李雅普诺夫函数(barrier Lyapunov function,简称BLF)设计状态控制约束器.文献[12]采用对称与非对称BLF,对一类带有不确定参数的非线性系统设计自适应控制器. 文献[13]采用时变BLF,对一类具有未知函数的非线性系统设计自适应控制器.文献[14]为限制永磁同步电机系统的电流设计控制器. 笔者拟对带有输入死区和输出受限的严格反馈系统,利用RBF神经网络设计控制器,且通过仿真示例验证控制器的有效性.
1 问题描述及预备知识
1.1 问题描述
考虑如下带有输入死区的非线性严格反馈系统
(1)
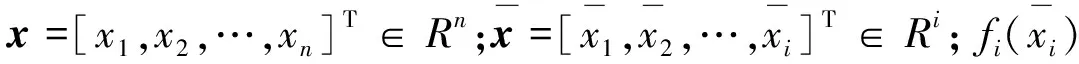
该文的控制目标是设计一个自适应神经网络控制器使系统的输出y跟踪给定的参考信号yd,同时保证闭环系统的所有信号均有界.为了实现控制目标,特提出如下假设:
假设1参考信号yd及其第i阶时间导数连续且有界,i=1,2,…,n.
1.2 障碍李雅普诺夫函数
对正定且连续可微的函数V(x),若x逼近含原点的邻域D的边界时,V(x)的值趋于无穷,则称V(x)为障碍型李雅普诺夫函数[11],其函数形式如下
(2)
引理1∀kb∈R为正常数,z1∈R在区间|z1|<|kb|,存在不等式[2]
(3)
其中: |y|≤kc,kb=kc-yd.
1.3 径向基函数神经网络
径向基函数(RBF)神经网络已被证明在有界闭集ΩZ⊂Rq上可以任意精度逼近连续函数,故笔者使用RBF神经网络去逼近未知的非线性函数.RBF神经网络方程如下
f(Z)=W*S(Z)+δ(Z),∀Z∈ΩZ,
(4)
其中:f(z)为待逼近的未知非线性函数;δ(Z)为逼近误差,|δ(Z)|<ε;W*为最优权重向量.高斯型径向基函数表达式为
(5)
其中:υi(i=1,2,…,l)为最优中心点;l为神经元节点数,且l>1;r为高斯函数的宽度.
1.4 输入死区特性
为研究方便,定义
(6)
其中:v(t)∈R为理想控制律;gl,gr为死区特性的左、右斜率;bl,br为左、右截距,且bl<0,br>0.
假设2[14]若函数gr(v)和gl(v)充分光滑,且存在未知正常数kl0,kl1,kr0,kr1,则有
0 (7) 0 (8) 将输入死区特性进行如下变换 u=D(v)=KT(t)Φ(t)v+d(v), (9) 其中 K(t)=[Kr(v(t)),Kl(v(t))]T, (10) Φ(t)=[φr(t),φl(t)]T, (11) (12) 其中:ξl(v)∈(v,bl),v 选取如下坐标变换 zi=xi-αi-1,i=1,2,…,n, (13) 其中:αi-1为自适应神经网络虚拟控制律,α0=yd. 自适应神经网络虚拟控制律、自适应律及理想控制律分别为 (14) (15) (16) 定理1在假设1、假设2及引理1的条件下,对于一类带有输入死区的严格反馈非线性系统(1),给定的初值满足|z1|<|kb|,设计一个自适应神经网络虚拟控制律如式(14)、自适应律如式(15)的控制器,则该控制器具有如下特性:(1)闭环系统的所有信号均半全局一致有界;(2)系统的输出满足约束条件;(3)系统的输出能跟踪期望信号. 证明步骤1 对z1求导得 (17) 选取李雅普诺夫函数为 (18) 对V1求导得 (19) (20) 将式(15)代入式(19)得 (21) 根据自适应律式(15),可得 (22) 步骤i对zi求导得 (23) 选取如下李雅普诺夫函数 (24) 对Vi求导得 (25) 同理,有如下不等式成立 (26) 根据式(14),(15),(26)整理式(25),可得 (27) 步骤n对zn求导得 (28) 选取如下李雅普诺夫函数 (29) 其中:β0≤min{kl0,kr0}为未知正定常数. 对Vn求导得 (30) 同理,有如下不等式成立 (31) 根据式(9),(31)整理式(30),可得 (32) 将式(16)代入式(32),整理可得 (33) 由引理1可知 (34) 令 则有 (35) 将式(35)两边乘ect,可得 (36) 对式(36)两边求积分,可得 (37) 令 则有 (38) 经推导,可得 (39) 类似可得 (40) 该文使用如下严格反馈非线性系统进行仿真分析 (41) 其中:u为系统的控制输入;ξ1(t)和ξ2(t)为有界扰动,ξ1(t)=sint,ξ2(t)=0.5sint. 控制目标为:系统输出y能够跟踪给定的参考信号yd=0.5(sint+sin0.5t). 选取控制信号u的输入死区特性为 (42) 选取自适应神经网络虚拟控制律、理想控制率及自适应律分别为 (43) (44) (45) 图1~4分别为系统输出、跟踪误差、控制信号及自适应律的仿真结果. 图1 系统输出 图2 跟踪误差 图3 控制信号 图4 自适应律 笔者针对带有输入死区和输出受限的严格反馈形式的非线性系统,设计了一种自适应神经网络控制器.利用RBF神经网络逼近系统的未知函数,使用障碍李雅普诺夫函数降低约束条件的影响.仿真结果表明该控制器具有有效性.
2 控制器设计


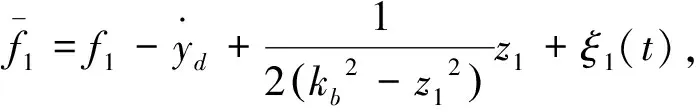



3 仿真分析





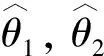
4 结束语

