具有平均跟踪性质的连续半流

王东明，牛应轩

(皖西学院 金融与数学学院，安徽 六安 237012)

设X为紧致度量空间，f:X→X连续，称(X,f)是一个离散动力系统. Blank为了研究动力系统的混沌性质，在文献[1]中引入了平均跟踪性质的概念.文献[2]的研究显示平均跟踪性质是刻画Anosov微分同胚的一个有用工具.许多研究者对具有平均跟踪性质的系统进行了深刻讨论，获得了许多丰富成果. 文献[3-5]研究具有平均跟踪性质与拓扑强遍历性等动力学性质之间的关系;文献[6]讨论具有平均跟踪性质的可扩系统的性质;文献[7-9]研究平均跟踪性质与其他跟踪性质的关联;文献[10]首次对于连续半流引入平均跟踪性质的概念.一个自然的问题是：具有平均跟踪性质的连续半流具有怎样的动力性质或者与其他动力性质有怎样的联系？ 作者对此做了更深入的讨论:对于具有平均跟踪性质的连续半流φ，证明了如果φ具有稠密的正上半密度回复点，则φ是拓扑传递的；进一步得到，如果φ具有满支撑，则φ×φ是拓扑遍历的.

1 预备知识

设(X,d)是具有度量d的紧致度量空间，+和分别表示全体非负实数构成的集合和全体正整数构成的集合.

φ:+×X→X称为连续半流，是指φ是连续的且满足：

(1) 对∀x∈X，φ(0,x)=x；

(2) 对∀x∈X，∀s,t∈R+，φ(s,φ(t,x))=φ(s+t,x).

点x∈X，集合r(x,φ)={φ(t,x):t∈R+}称为φ的经过x的轨道. 如果对X的任意非空开集U,V∈X，都存在t∈R+，使得φ(t,U)∩V≠∅，则称φ是拓扑传递的.

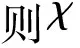
下面引入连续半流的平均跟踪性质的概念.

对于连续半流φ，如果对∀ε>0，存在δ>0，使得φ的每个(δ,1)-平均伪轨都被φ的经过某个点的轨道ε-平均跟踪，则称φ具有平均跟踪性质.

2 主要结果及证明

定理1设(X,d)为具有度量d的紧致度量空间，φ:+×X→X是一个连续半流. 如果φ具有平均跟踪性质且φ的具有正上半密度的回复点集是稠密的，即则φ是拓扑传递的.

(1)

(2)

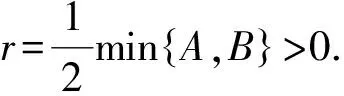
(i) 2ni4；

定义X中的一个点序列{yj}+∞j=0为

即

y0=x,y1=φ(1,x),…,yn1-1=φ(n1-1,x),yn1=φ(n1,y),…,yn2-1=φ(n2-1,y)，

yn2=φ(n2,x),…,yn2i=φ(n2i,x),…,yn2i+1-1=φ(n2i+1-1,x),yn2i+1=φ(n2i+1,y),… .

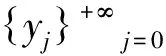
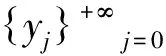
(3)

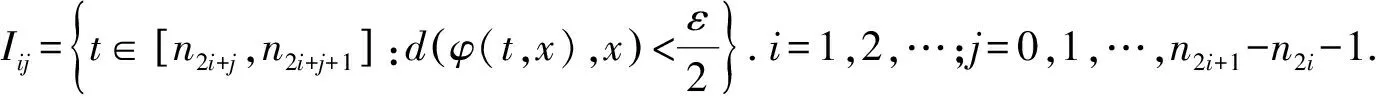
如果L⊂R+，l(L)表示L的Lebesgue测度.

断言1对每个i∈，有

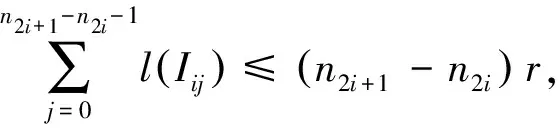
这与(ii)矛盾，所以断言1成立.

由(3)式可得，存在无限多个i∈，使得对每个这样的i，有

(4)

对这样的每个i，记

因而,有

这与(4)式矛盾，因而断言2成立.

由断言1与断言2，可以得到：存在无限多个i∈，使得对每个这样的i，∃t∈[n2i,n2i+1]，使得且因此d(φ(t,z),x)<ε.

类似可以证明存在无限多个i∈，使得对每个这样的i，存在t∈[n2i-1,n2i],满足d(φ(t,z),y)<ε.

因此，可以取得t1,t2∈+且t2>t1,满足d(φ(t1,z),x)<ε及d(φ(t2,z),y)<ε. 那么φ(t1,z)∈U，φ(t2,z)∈V，从而φ(t2-t1,U)∩V≠∅，即存在t=t2-t1>0，满足φ(t,U)∩V≠∅， 所以φ是拓扑传递的. 定理1证毕.

设(X,d)为具有度量d的紧致度量空间，积X×X上的度量ρ定义为：对任意(x,y),(x′,y′)∈X×X，ρ((x,y),(x′,y′))=max{d(x,x′),d(y,y′)}，对任意t∈+及(x,y)∈X×X，定义φ×φ(t,(x,y))=(φ(t,x),φ(t,y))，那么φ×φ:+×(X×X)→X×X为连续半流.

由定义，可以容易地证明下面的引理1.

引理1设(X,d)为紧致度量空间，φ:+×X→X为连续半流，则φ具有平均跟踪性质当且仅当φ×φ具有平均跟踪性质.

引理2设X为紧致度量空间，φ:+×X→X为连续半流. 如果φ具有满支撑，则存在μ∈M(φ,X)，使得supp(μ)=X

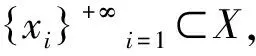
引理3设X为紧致度量空间，φ:+×X→X是一个连续半流. 如果φ具有满支撑，则φ的正上半密度回复点稠密.

证明因为φ具有满支撑，则由引理2知，存在μ∈M(φ,X),使得supp(μ)=X. 设U⊂X为X的非空开集，则μ(U)>0. 由遍历分解定理[11]知，存在φ的遍历测度m，使得m(U)>0.

事实上，对∀ε>0，m(V(y,ε))>0. 取一个连续函数f:X→+，满足：对∀x∈X，0≤f(x)≤1，f(y)=1且当x∈XV(y,ε)时，f(x)=0.则

所以y为φ的正上半密度回复点. 因为y∈U，且U为X的任一个非空开集，故φ有稠密的正上半密度回复点.

引理4[13]如果X为紧致度量空间，φ:+×X→X为拓扑传递的连续半流，且存在μ∈M(φ,X)，使得supp(μ)=X，则φ是拓扑遍历的.

定理2设X为紧致度量空间，φ:+×X→X为连续半流. 如果φ具有平均跟踪性质且具有满支撑，则φ×φ是拓扑遍历的.

证明因为φ具有满支撑，由引理2知，存在μ∈M(φ,X)，使得supp(μ)=X. 显然μ×μ∈M(φ×φ,X×X). 因为supp(μ×μ)⊇suppμ×suppμ=X×X. 所以supp(μ×μ)=X×X, 从而φ×φ具有满支撑. 又由引理3得，φ×φ具有稠密的正上半密度回复点. 由引理1知φ×φ具有平均跟踪性质，所以根据定理1得φ×φ是拓扑传递的. 又由引理2及引理4得到φ×φ是拓扑遍历的.