算子代数上的可乘左导子

贾 娟

(太原学院 应用数学系，山西 太原 030032)

0 引言

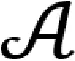
一般地，若对上面的映射δ没有任何线性或可加假设，则称δ为可乘(Jordan)左导子.关于环与算子代数上的各类可乘映射何时是可加的问题，一直备受许多学者的关注.本文的目的是考虑算子代数上可乘左导子的结构性质.

本文首先在一般的环上讨论可乘左导子的结构性质,之后再把该结果应用于算子代数上.结构如下.令是含有单位元1和非平凡幂等元e1的环.假设δ ：→是可乘左导子.本文首先给岀了δ的结构性质，即其定满足：

(i)δ(ei)=0，δ(eiej)=δ(eiejei)={0}，ejδ(eiei)={0}，ejeiδ(eiei)={0},其中i≠j∈{1,2}，e2=1-e1.

(ii)存在可乘左导子δij:eiei→eiej使得对所有x∈成立,i，j∈{1,2}.特别地，若δ在eiei(i= 1，2)上是可加的，则(i)与(ii)是δ成为可乘左导子的充要条件(定理1).在此基础上，得到了三角环上可乘左导子的完全刻画(见推论2),证明了素环上不存在非零的可乘左导子(推论3)，进而得到标准算子代数与因子von Neumann代数上均不存在非零的可乘左导子(推论4-5).

1 主要结果及其应用

本节将在一般环上研究可乘左导子的刻画问题，之后再把该结果应用于算子代数上.

下面是本节的主要结果.

定理1令是含有单位元1和非平凡幂等元e1的环.假设δ :→是可乘左导子，则下列表述成立：

1)δ(ei)=0，δ(eiej)=δ(eiejei)={0},其中i≠j∈{1,2}，e2=1-e1.

2)ejδ(eiei)={0}，ejeiδ(eiei)={0},其中i≠j∈{1,2}.

3)存在可乘左导子δij:eiei→eiej使得对所有x∈成立,i，j∈{1,2}.

特别地，若δ还满足条件δ(eixei+eiyei)=δ(eixei)+δ(eiyei)(i = 1，2)对所有元x,y∈成立，那么δ是可乘左导子当且仅当上面的表述1)-3)成立.

断言1δ(0)=0.

显然有δ(0)=δ(0·0)=0·δ(0)+0·δ(0)=0.

断言2δ(e1)=δ(e2)=0.

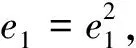
(1)

类似可证δ(1-e1)=0.

断言3δ(ij)={0}，i≠j∈{1,2}.

对任意元x12∈12，由断言2有

δ(x12)=δ(x12(1-e1))=x12δ(1-e1)+(1-e1)δ(x12)=(1-e1)δ(x12).

此式蕴含e1δ(x12)=0.

另一方面，由断言2有

δ(x12)=δ(e1x12)=x12δ(e1)+e1δ(x12)=e1δ(x12).

此式蕴含(1-e1)δ(x12)=0.进而得到δ(x12)=0对所有x12∈12成立.

δ(21)={0}的证明类似可得，省略之.

由断言3以及δ的性质易验证δ(eiejei)={0},其中i≠j∈{1，2}.由此，结合断言2-3知，表述1)成立.

断言4对任意元xii∈ii，我们有ejδ(xii)=0与jiδ(xii)={0},i≠j∈{1,2}.

对任意元x11∈11，由断言1-2有：

0=δ(x11(1-e1))=x11δ(1-e1)+(1-e1)δ(x11)=(1-e1)δ(x11).

再任取x12∈12，并利用断言3,可得：

0=δ(x21x11)=x21δ(x11)+x11δ(x21)=x21δ(x11).

同理可证，对任意元x22∈22与x21∈21,我们有：

e1δ(x22)=0，x12δ(x22)=0.

由断言4知,表述2)成立.

断言5对任意元x11∈11与x12∈12，我们有δ(x11+x12)=δ(x11).

对任意的x11∈11和x12∈12，由断言1和2,有：

δ(x11)=δ((x11+x12)e1)=e1δ(x11+x12)+(x11+x12)δ(e1)=e1δ(x11+x12)

(2)

和

0=δ((1-e1)(x11+x12))=(1-e1)δ(x11+x12)+(x11+x12)δ(1-e1)=

(1-e1)δ(x11+x12).

(3)

结合(2)、(3)式，得到δ(x11+x12)=δ(x11)对所有x11∈11和x12∈12成立.

断言6对任意元x12∈12与x22∈22，我们有δ(x12+x22)=δ(x22).

证明与断言5类似，省略之.

断言7对任意的x∈,我们有δ(x)=δ(e1xe1)+δ(e2xe2).

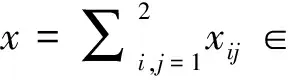
δ(x11)=δ(x11+x12)=δ(e1(x11+x12+x21+x22))=

e1δ(x11+x12+x21+x22)+(x11+x12+x21+x22)δ(e1)=

e1δ(x11+x12+x21+x22)=e1δ(x)

与

δ(x22)=δ(x12+x22)=δ((x11+x12+x21+x22)(1-e1))=

(1-e1)δ(x11+x12+x21+x22)+(x11+x12+x21+x22)δ(1-e1)=

(1-e1)δ(x11+x12+x21+x22)=(1-e1)δ(x).

因此δ(x)=δ(x11)+δ(x22).

注意到，由断言4知，δ(ii)⊆ii+ij(i≠j∈{1,2}).现在定义映射δij:eiei→eiej为：

δij(eixei)=eiδij(x)ej,∀x∈,i,j=1,2.

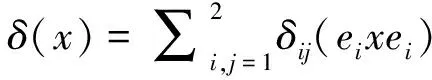
特别地，假设δ还满足条件δ(eixei+eiyei)=δ(eixei)+δ(eiyei)对所有元x,y∈成立，其中i=1,2.为了完成定理的证明，只需验证，若表述1)-3)成立，则δ定是可乘左导子.

δ(xy)=δ(x11y11+x12y21)+δ(x21y12+x22y22)=δ(x11y11)+δ(x12y21)+δ(x21y12)+δ(x22y22)=

δ11(x11y11)+δ12(x11y11)+δ21(x22y22)+δ22(x22y22)

(4)

另一方面，可得

xδ(y)+yδ(x)=x(δ(y11)+δ(y22))+y(δ(x11)+δ(x22))=x11δ11(y11)+x11δ12(y11)+

x22δ21(y22)+x22δ22(y22)+y11δ11(x11)+y11δ12(x11)+y22δ21(x21)+y22δ22(x22)=

δ11(x11y11)+δ12(x11y11)+δ21(x22y22)+δ22(x22y22)

(5)

比较(4)、(5)，即得δ(xy)=xδ(y)+yδ(x).

定理得证.

若定理1中的映射是可加的，则可给出一般环上可加左导子的完全刻画.

推论1令是含有单位元1和非平凡幂等元e1的环.假设δ:→是可加映射.则δ是左导子当且仅当下列表述成立：

1)δ(ei)=0,δ(eiejei)={0},其中i≠j∈{1,2},e2=1-e1.

2)ejδ(eiei)={0},ejeiδ(eiei)={0}，i≠j∈{1,2}.

3)存在可加左导子δij:eiei→eiej,使得对所有x∈成立，i,j∈{1,2}. 下面给出定理1的几个应用.

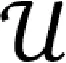
显然，三角环满足定理1中的条件.利用定理1到三角环上，可得下面的结论,其推广了文献[10]中的定理2.1.

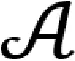
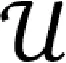
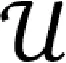
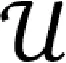
使得δ(X)=δ11(P1XP1)+δ12(P1XP1)+δ22(P2XP2)

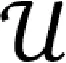
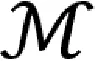
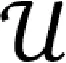
X=P1XP1+P1XP2+P2XP2=X11+X12+X22，

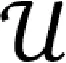
利用表述1)-3),我们有

δ(XY)=δ(X11Y11+X11Y12+X12Y22+X22Y22)=

δ11(X11Y11)+δ12(X11Y11)+δ22(X22Y22)

(6)

和

Xδ(Y)+Yδ(X)=X(δ11(Y11)+δ12(Y11)+δ22(Y22)) +Y(δ11(X11)+δ12(X11)+δ22(X22))=

X11δ11(Y11)+X11δ12(Y11)+X12δ22(Y22)+X22δ22(Y22)+Y11δ11(X11)+Y11δ12(X11)+Y12δ22(X22)+

Y22δ22(X22)=X11δ11(Y11)+X11δ12(Y11)+X22δ22(Y22)+Y11δ11(X11)+Y11δ12(X11)+Y22δ22(X22)=

δ11(X11Y11)+δ12(X11Y11)+δ22(X22Y22).

(7)

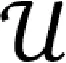
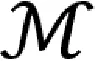
证毕.

推论3令是含有单位元1与非平凡幂等元e1的素环.则上不存在非零的可乘左导子.

证明 假设δ是上可乘左导子.显然,满足定理1中的条件.那么，利用定理1可知表述1)-3)均成立.特别地,对于表述(2)中的式子ejeiδ(eiei)={0}(i≠j∈{1,2}),由的素性可得eiδ(eiei)={0}.该式再结合表述，即得δ(eiei)={0}.因此表述3)蕴涵δ(x)=0对所有元x∈均成立.所以δ≡0.证毕.

众所周知，标准算子代数是素的.利用推论3,下面的结论是显然的.

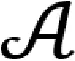
注意到每个因子von Neumann代数是素的.由推论3立得下面结论.

推论5因子von Neumann代数上不存在非零的可乘左导子.