基于四阶非线性偏微分方程的精确解探讨

吴丽娇

(福建船政交通职业学院，福建 福州 350000)

0 引言

经过多年的研究，求非线性微分方程精确解的方法变得越来越多，许多学者利用不同方法在研究一些典型的非线性方程中，已经获得了一些很有意义的解.并且已经发现很多典型的非线性偏微分方程有丰富的行波解.近年来，像积分分支法，广义椭圆方程法，F-展开法等都被广泛运用于求解非线性偏微分方程的领域中.这三种数学方法一直都是非线性分析很好的工具.除此之外，还发现了很多其他求解非线性偏微分的方法，例如：逆散射方法，扩展的双曲正切方法，维尔斯特拉斯函数方法，指数函数展开法方法，对称性方法，Baclund变换方法，同伦分析方法，达布变换方法，广田的双线性方法，正弦余弦方法，平面动力系统分支方法，辅助方程方法和The simpleast equation方法等等.吴登辉等人(2017)提出利用四阶偏微分方程计算方法，结合图像去噪可以有效去除图像中的斑点噪声[1].代慧菊等人(2019)提出利用Bäcklund变换结合李对称分析方法、幂级数展开法获得精确解[2].官翠婷等人(2018)提出结合Jensen不等式解决方程初边值问题可以产生爆破现象[3].基于此，可以看出，利用简便方法获得了一些非线性偏微分方程的很多孤立子解和周期波解，同时在简便方法的基础上进行改进，提出了一种新的简便方法，并将其应用于求解.

1 一阶非线性偏微分方程确定方法

1.1 一阶非线性偏微分方程

经过多年的研究，求非线性微分方程精确解的方法变得越来越多，许多学者利用不同方法在研究一些典型的非线性方程中，已经获得了一些很有意义的解.并且已经发现很多典型的非线性偏微分方程有丰富的行波解.例如： CH方程：ut-uxxt+2kux+3uux=2uxuxx+uuxxx，有孤立尖波解等行波解.CH-γ方程：ut+c0ux+3uux-α2(uxxt+uuxxx+3uxuxx)+γuxxx=0，有紧孤子解和广义纽子波解.著名的KdV方程：ut-6uux+uuxxx=0，有光滑的孤立波解.除此之外，还有double Sine-Gordon方程，Variant Boussinesq方程，(2+1)-dimensional KdV方程都有丰富的行波解.运用这种简便方法求解下面四阶非线性偏微分方程如(1)所示：

(ku+γu2)xx+μuxxtt=νuuxxxx+αuxuxxx+βuxx2+utt，

(1)

到目前为止，已有一些学者对此进行研究，例如Meleshko用一种新算法将该方程转换成三阶线性偏微分方程.Clarkson和Priestley用推广的tanh方法和cosh-sinh方法求出了该方程的周期波解，类孤子解等.

1.2 非线性波方程

对于一个关于独立变量u的一类非线性偏微分方程如(2)所示：

H1(u,ux,ut,uxx,uxt,utt,…)=0，

(2)

该方法通过下面四个步骤寻找非线性偏微分方程的精确解：

步骤一: 如(3)所示

u(x,t)=φ(x,t)+R

(3)

其中R任意常数，将变换(3)代入(2)中，则(2)转换为下面的形式，如(4)所示：

H2(φ,φx,φt,φxx,φxt,φtt,…)=0.

(4)

步骤二: 确定常数R的值.

令

Φ=φ-α2φxx

(5)

其中α≠0.将(5)代入(4)中，使(4)的各项表达式都包含Φ或者Φ的各阶导数，根据方程各项之间系数的关系，得出R的取值.

例如：考虑如下偏微分方程[4]，如(6)所示：

ut+2kux-uxxt+2uux=uxuxx+uuxxx

(6)

其中k是一个常数.将(3)带入(6)中结果如(7)所示：

φt+2kφx-φxxt+2φφx+2Rφx=φxφxx+φφxxx+Rφxxx

(7)

(7)可转换如(8)所示：

(φ-φxx)t+φx(φ-φxx)+φ(φ-φxx)x=-(2R+2k)φx+Rφxxx

(8)

由(5)计算，取α2=1得如(9)所示：

Φt+φxΦ+φΦx=-(2R+2k)φx+Rφxxx

(9)

为了使(9)的每一项都包含Φ或者Φ的各阶导数，必须如(10)所示：

-(2R+2k)=-R

(10)

即，如(11)所示：

R=-2k.

(11)

将(11)代入(9)得如(12)所示：

Φt+φxΦ+φΦx=2kΦx.

(12)

步骤三: 求解方程Φ=0的解.注意到Φ=φ-φxx=0是一线性偏微分方程，因此容易得到该方程的更一般形式的解.

步骤四: 获得(2)的精确解.(5)的变形，(12)的每一项都包含Φ或者Φ的各级导数.则当φ(x,t)是方程Φ=0的解时，φ(x,t)也是(4)的解.实际上，在(12)中，当φ(x,t)是方程Φ=0的解时，φ(x,t)也是(12)的解.通过改变常数t的取值来扩展方程Φ=0的基础解，从而得到(2)的一系列的精确解.

1.3 算法模拟扩展

假如当(2)可化为-kΦxx-Φtt=0的形式时，可令Φ=ct+dx或Φ=φ-φxx=x2-kt2，当φ(x,t)是方程φ-φxx=ct+dx的解或是φ-φxx=ct2-kx2解时，则它也是(2)的解.在计算过程的第四步中，只要在方程Φ=ct+dx或Φ=x2-kt2的基础解之上进行扩充，就可以得到(2)的一系列精确解.从以上的构造可以看出，根据不同的方程，使Φ取不同的形式，最终只要能够转化为每一项都包含Φ或者Φ的各阶导数的方程，就可以用这种扩展后的简便方法求解[5].

2 一类四阶非线性偏微分方程的求解

2.1 精确解

运用这种简便方法求解四阶非线性偏微分方程如(13)所示：

(ku+γu2)xx+μuxxtt=νuuxxxx+αuxuxxx+βuxx2+utt

(13)

其中k，γ，μ，ν，α，β为任意常数.令u(x,t)=φ(x,t)+R，将其代入(13)的结果如(14)所示：

(k+2γR)φxx+2γφx2+2γφφxx+μφxxtt-νφφxxxx-νRφxxxx-

αφxφxxx-βφxx2-φtt=0

(14)

根据步骤二，(14)可转换如(15)所示：

((k+2γR)φ-νRφxx)xx+φx(2γφ-αφxx)x+φ(γφ-νφxx)xx+

φxx(γφ-βφxx)-(φ-μφxx)tt=0.

(15)

令Φ=φ-φxx，为了使(15)的每一项包含Φ或者Φ的各级导数，则(15)的系数必须满足如(16)所示：

μ=1,2γ=α,γ=β,γ=ν,k+2γR=νR

(16)

求解(16)得如(17)所示：

(17)

则(15)可变为如(18)所示：

-k(φ-φxx)xx+2γφx(φ-φxx)x+γφ(φ-φxx)xx+

γφxx(φ-φxx)-(φ-φxx)tt=0

(18)

注意到Φ=φ-φxx，(18)可变为如(19)所示：

-kΦxx+2γφxΦx+γφΦxx+γφxxΦ-Φtt=0

(19)

2.2 情形计算模拟

当γ≠0时，考虑方程Φ=0.即如(20)所示:

φ-φxx=0

(20)

容易求出(20)的基本解组如(21)所示：

φ(x,t)=A(t)ex+B(t)e-x

(21)

其中A(t)，B(t)是任意函数.当B(t)=0时，如(22)所示：

φ(x,t)=A(t)ex

(22)

当A(t)=0时，如(23)所示：

φ(x,t)=B(t)e-x

(23)

则(22)和(23)均为(20)的解，如(24)、(25)所示：

(24)

(25)

可得(26)、(27)也是(20)的解：

φ(x,t)=B(t)e|x|

(26)

φ(x,t)=B(t)e-|x|

(27)

此外，当A(t)≠B(t)时，由(24)、(25)同样可以构造如(28)所示：

(28)

从而可以得出如(29)也是(20)的解：

φ(x,t)=A(t)e|x|+B(t)e-|x|

(29)

由于A(t)，B(t)是任意函数，则可以扩展解(21)如(30)所示[6]：

φ(x,t)=A(t)ex-c1t+B(t)e-x+c2t

(30)

其中c1，c2为任意常数.

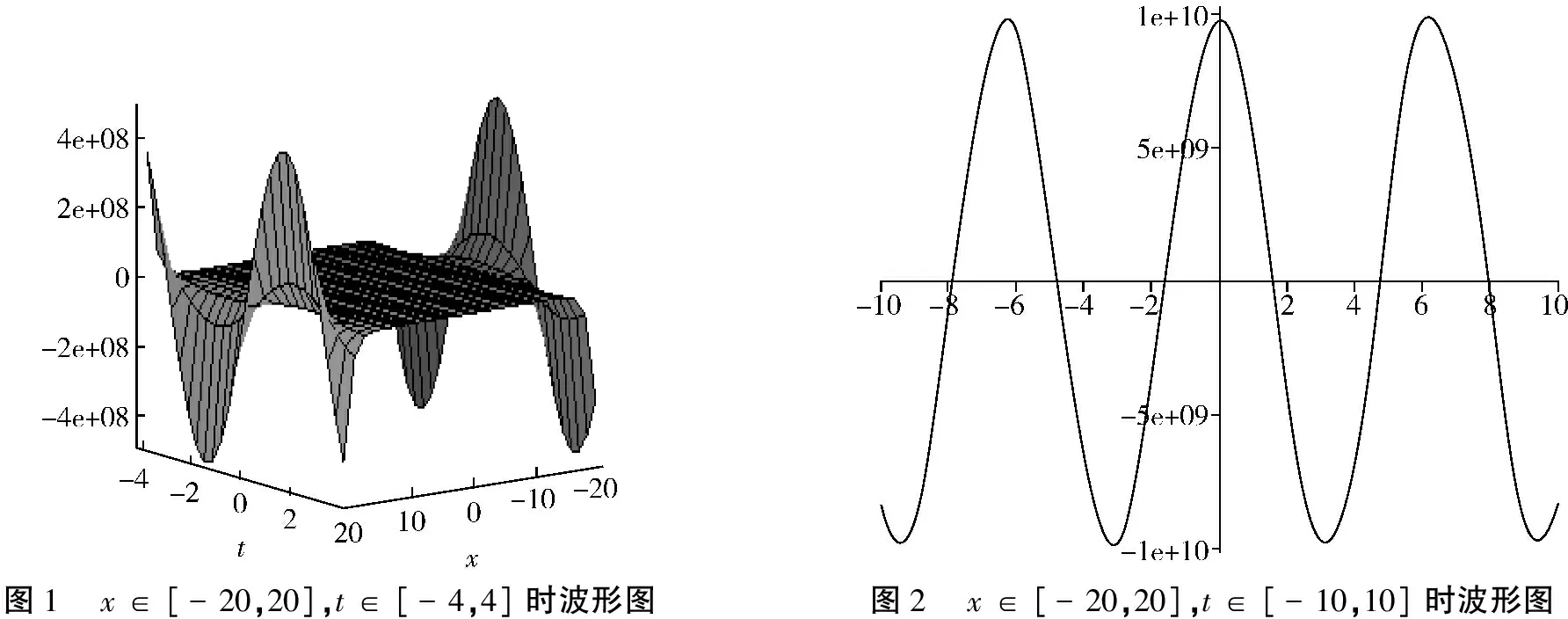
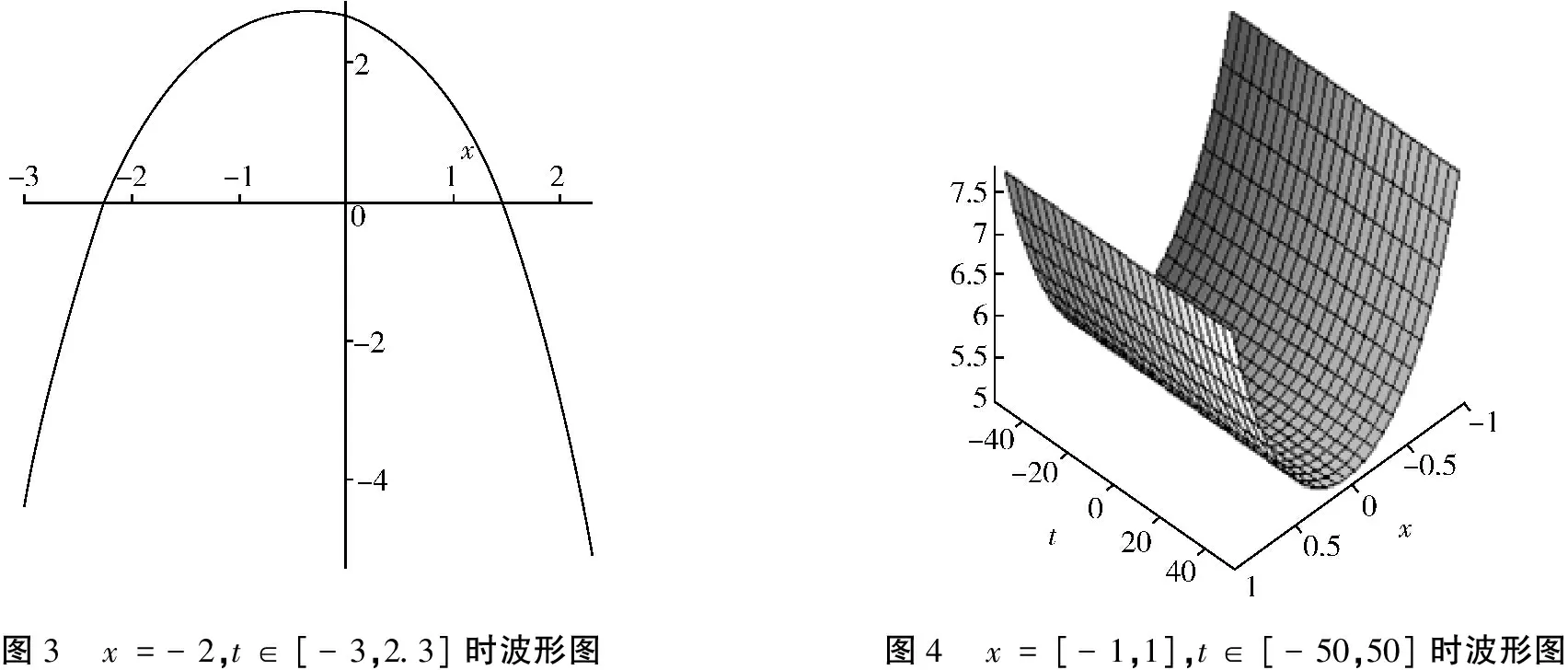
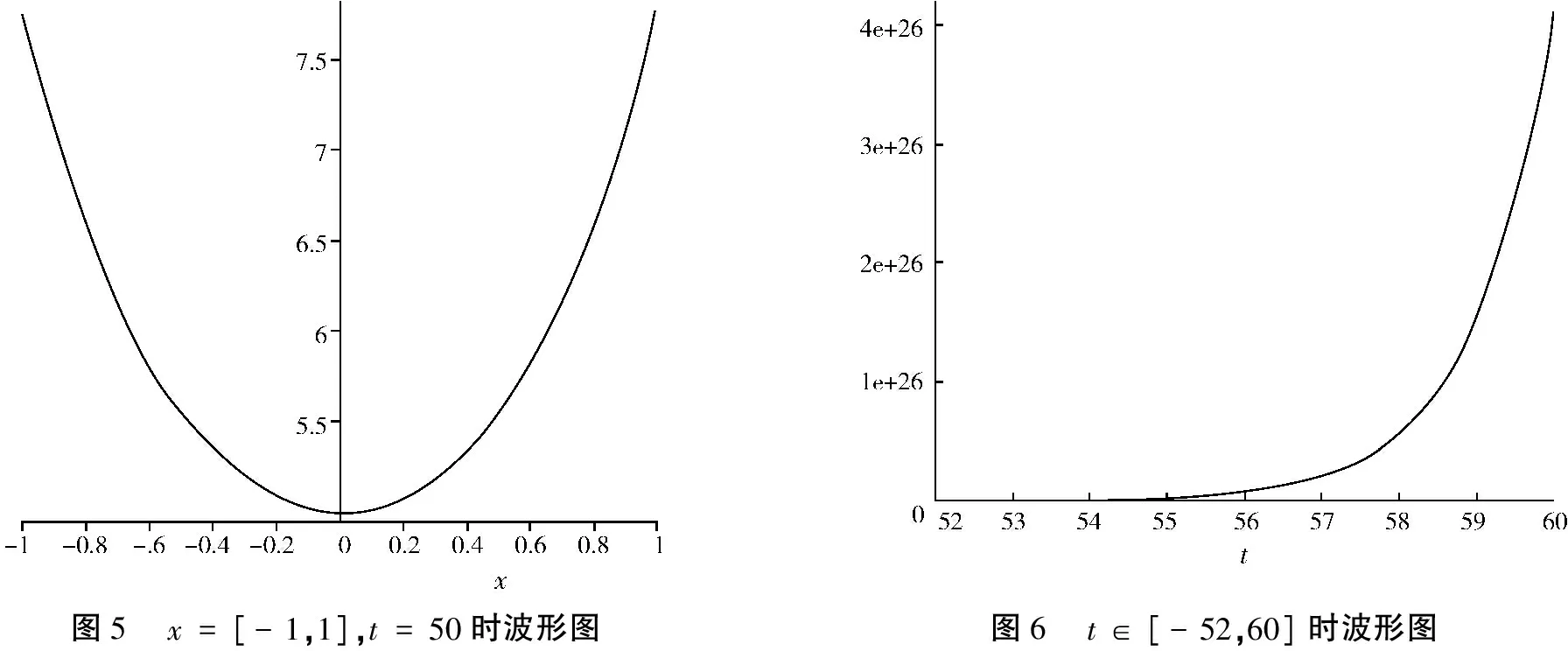
不妨假设00时，则有0

(31)

从(31)中可以得出如(32)也是(20)的解：

φ(x,t)=A(t)e|x-c1t|+B(t)e-|x-c2t|

(32)

除此之外，还能扩展(21)如(33)所示：

φ(x,t)=A(t)ex-p(t)+B(t)e-x+q(t)

(33)

其中p(t)，q(t)为任意函数.通过检验，(33)也是(20)的解.

相类似地，由于p(t),q(t)是任意函数，不妨设0

(34)

由(34)可以得如(35)也是(20)的解：

φ(x,t)=A(t)e|x-p(t)|+B(t)e-|x-q(t)|

(35)

(36)

(37)

其中Ai(t),Bj(t),pi(t),和qj(t)是任意函数，i=1,2,···,N；j=1,2,…,M和N,M是任意正整数.类似构造(20)的解，可得如(38)、(39)所示也是(20)的解：

(38)

(39)

根据双曲函数的定义，(20)不同表达形式的特殊解可通过(36)、(37)构造出来，如(40)、(41)所示：

(40)

(41)

构造(20)的shockpeakon解，每一种shockpeakon解的形式类似如(42)所示：

(42)

其中A,B是任意常数且A≠B.因此(20)有下面形式的解，如(43)所示:

φ(x,t)=Ae-|x|-Bsgn(x)e-|x|

(43)

再通过(44)计算：

(44)

可得如(45)同样也是(20)的shockpeakon解：

φ(x,t)=A(t)e-|x|-B(t)sgn(x)e-|x|

(45)

同理可得如(46)也是(20)的shockpeakon：

φ(x,t)=A(t)e-|x-p(t)|-B(t)sgn(x)e-|x-p(t)|

(46)

它能通过如(47)构造出来：

(47)

其中x是任意给定的常数.类似的，(43)，(45)，(46)也可以扩展为如(48)-(50)所示：

(48)

(49)

(50)

值得注意的是，从上面的这些构造过程中，可以得到(20)的其它精确解.

当k≠0，γ=0时，则(19)可化为如(51)所示：

-kΦxx-Φtt=0

(51)

此时，有两种设法可解(51).

方法一 如(52)所示：

Φ=φ-φxx,φ-φxx=cx+dt

(52)

其中c,d是任意常数.

通过计算可以求出(52)的基本解组为如(53)所示：

φ(x,t)=A(t)ex+B(t)e-x+cx+dt

(53)

其中A(t),B(t)是任意函数.

同理，通过扩展基本解组，可得(53)的下列解，如(54)-(62)所示：

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

满足(52)的解也是(51)的解.

方法二 如(63)所示:

Φ=φ-φxx,φ-φxx=x2-kt2

(63)

其中k是任意常数.它的基本解组如(64)所示：

φ(x,t)=A(t)ex+B(t)e-x+2-kt2+x2

(64)

其中A(t),B(t)是任意函数.

同理，通过扩展基本解组，可得(63)的下列解，如(65)-(73)所示：

(65)

(66)

(67)

(68)

(69)

(70)

(71)

(72)

(73)

满足(63)的解也是(51)的解.

2.3 精确解波形图分析

根据所求得的精确解，利用Maple软件将几个典型的波形图绘制如图所示：

绘图时都取γ=1,k=-4,M=1,N=1.

1)A(t)=sin(t),B(t)=cos(t),x∈[-20,20],t∈[-4,4]时，其波形图如图1所示.

2)A(t)=sin(t),B(t)=cos(t),x∈[-20,20],t∈[-10,10]时，其波形图如图2所示.

3)A(t)=sin(t),B(t)=cos(t),x=-2,t∈[-3,2.3]时，其波形图如图3所示.

4)A(t)=sinh(t),B(t)=cosh(-t),x=[-1,1],t∈[-50,50]时，其波形图如图4所示.

5)A(t)=sinh(t),B(t)=cosh(-t),x=[-1,1],t=50时，其波形图如图5所示.

6)A(t)=sinh(t),B(t)=cosh(-t),t∈[-52,60]时，其波形图如图6所示.

图1 x∈[-20,20],t∈[-4,4]时波形图图2 x∈[-20,20],t∈[-10,10]时波形图

图3 x=-2,t∈[-3,2.3]时波形图图4 x=[-1,1],t∈[-50,50]时波形图

图5 x=[-1,1],t=50时波形图图6 t∈[-52,60]时波形图

3 结论

研究求解非线性偏微分的精确解.得出了一种有效简便方法来求解.和其他方法相比较，这种方法更简单直接，避免了很多繁琐重复的计算步骤.用这种简便方法求解一类四阶非线性偏微分方程，得到了它的一般解的表现形式.利用数学软件MAPLE，通过参数取值得了该方程的一些特殊解，包括孤立子精波解、单峰解、多峰解、多重波解、紧孤子解，广义纽子波解、呼吸子解、爆破波峰解、三角函数解、双曲函数解及它们的混合解.