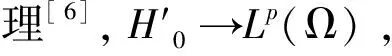一类变系数波方程耦合系统整体解的性质

兰 杰

(山西财贸职业技术学院，山西 太原 030031)

0 引言

本文研究的是变系数波动方程耦合系统：

(1)

带阻尼项的变系数波动方程，在文献[4-5]中都进行了深入的讨论，这篇文章主要对p,q在合适的假设下，在系统(1)[1，3]在[0,T]上存在唯一的局部解(u,v)[3]的基础上，讨论具有阻尼项和源项的变系数波动方程耦合系统(1)解的整体存在性以及能量的多项式衰减.以下文章主要分为两部分，第一部分给出了本文的主要结论，第二部分对相关引理和主要结论进行了证明.

1 主要结论

同文献[1]，引入相同的黎曼流形中的一些符号，我们可以得到如下主要结论.

定理1(解的整体存在性)假设存在θ使得

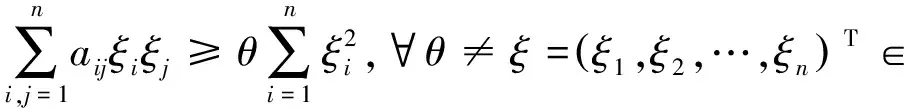
p满足

1

并且(u0,v0)∈S,(u,v)∈L2(Ω)×L2(Ω)满足：

(2)

则系统(1)存在一个整体解(u,v)满足：

定理2(解的衰减性质)若定理1的条件成立，并且q满足2

2 主要结论的证明

2.1 证明主要结论之前，需要引入如下几个重要引理

引理1[2]令y(t):+→+是一个非增函数，并假设存在常数β>1和A>0使得

则

引理2设(u,v)是系统(1)的解，则E(t)满足：

(3)

注：易得E(t)是一个非增函数，即：

E(t)≤E(0),∀t∈[0,)

(4)

引理3[3]假设p满足

1

(u0,v0)∈S,(u1,v1)∈L2(Ω)×L2(Ω)满足(2)式.

则(u,v)∈S,∀t∈[0,T)并且有

(5)

2.2 主要结论的证明

定理1的证明

可得

(6)

其中

(7)

类似可得：

(8)

(9)

(10)

将(7)-(10)式代入(6)式可得

取ε充分小，使得

令T→，则有

运用引理1，有

证毕.

即可知，若定理1的条件成立，并且q满足2