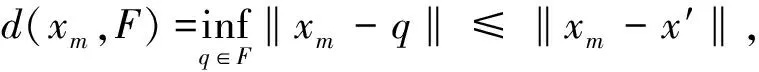严格伪压缩半群迭代序列的强收敛定理

张树义，张芯语

(渤海大学 数理学院,辽宁 锦州 121013)

设E是实Banach空间,E*为E的对偶空间，〈·,·〉表示E与E*之间的广义对偶对.正规对偶映象J:E→2E*定义为J(x)={f∈E*:〈x,f〉=‖x‖2=‖f‖2},∀x∈E.设C是E的非空凸子集,T:C→C是一映象,用F(t)表示映象T的不动点集.

定义1映象集合{T(t):t∈R+}:C→C被称为严格伪压缩半群,如果满足下列条件:

(i)T(0)x=x,∀x∈C；

(ii)T(s+t)x=T(s)T(t)x,∀x∈C,∀s,t∈R+；

(iii) ∀x∈C,映象T(·)x从R+到C是连续的;

全文设F:=∩t≥0F(T(t)),λ=inft≥0λ(t),λ>0.

定义2(i) 映象T:C→C被称为伪压缩的,如果对∀x,y∈C,存在

j(x-y)∈J(x-y),

使得

〈Tx-Ty,j(x-y)〉≤‖x-y‖2.

(ii)T:C→C被称为强伪压缩的,如果存在k∈(0,1),对∀x,y∈C,存在j(x-y)∈J(x-y),使得

〈Tx-Ty,j(x-y)〉≤k‖x-y‖2.

(iii)T:C→C被称为依Browder和Petryshyn意义严格伪压缩的,如果存在λ>0,对∀x,y∈C,存在j(x-y)∈J(x-y),使得

〈Tx-Ty,j(x-y)〉≤‖x-y‖2-λ‖(I-T)x-(I-T)y‖2.

(1)

注1Browder-Petryshyn型严格伪压缩映象一定是Lipschitz连续的.事实上,由式(1),有

λ‖(x-y)-(Tx-Ty)‖2≤‖(x-y)-(Tx-Ty)‖‖j(x-y)‖，

又

λ[‖(Tx-Ty)‖-‖x-y‖]≤‖(x-y)-(Tx-Ty)‖,

因此

λ[‖(Tx-Ty)‖-‖x-y‖]≤‖x-y‖,

即

由此,如果{T(t):t≥0}是C上严格伪压缩半群,则对∀t>0,∀x,y∈C,有

‖T(t)x-T(t)y‖≤L(t)‖x-y‖.

xn=αnxn-1+(1-αn)T(tn)xn,n≥1.

(2)

引理1设E是Banach空间,J:E→2E*是正规对偶映象,则∀x,y∈E,有

‖x+y‖2≤‖x‖2+2〈y,j(x+y)〉,∀j(x+y)∈J(x+y).

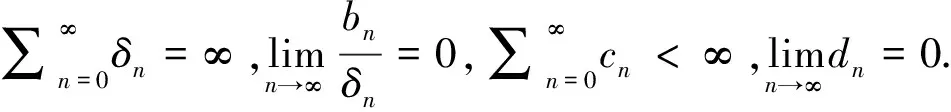
(3)

由Ψ单调增加以及∀t>0,Ψ(t)>0,有

对∀n≥n2,由(3)式可知

(4)

当k=N,(4)式显然成立.假设当k≥N成立,往证对k+1成立.假设结论不成立,则

从而ak+1>ε.由Ψ的单调增加以及∀t>0,Ψ(t)>0,有

从而由(3)式,有

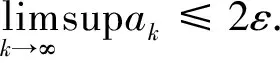
1 主要结果

xn=αnxn-1+(1-αn-βn)T(tn)xn+βnT(tn)xn-1,∀n≥1.

(5)

证明由(5)式,有

(6)

由(6)式,有

(7)

由引理1及(7)式,对任意p∈F(t),存在j(xn-p)∈J(xn-p),使得

‖xn-p‖2=‖xn-1-p+xn-xn-1‖2≤‖xn-1-p‖2+2〈xn-xn-1,j(xn-p)〉=

(8)

(9)

因

‖xn-T(tn)xn‖≤‖xn-T(tn)xn‖+‖T(t+tn)xn-T(tn)xn‖+

以及{T(t):t≥0}满足条件(A),所以

(10)

从而由(9),(10)式,∀n>n1,有

上式对p∈F取下确界，有

(11)

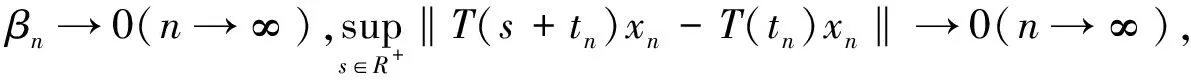
其中

Q=max{‖xn2-x′‖,‖xn2+1-x′‖,…,‖xm-1-x′‖,‖xm-x′‖},

显然0

d(xn,F)≤Q.

(12)

这是一个矛盾.因此当∀n≥m时,(12)式成立.于是,由(11)式,∀n≥m,有

(13)