基于DE-SVM的硅基压阻式压力传感器温度补偿研究∗

文常保，王 蒙，钟晨昊，宿建斌，巨永锋

(长安大学电子与控制工程学院微纳电子研究所，西安710064)

在工业生产领域，硅基压阻式压力传感器以其小体积、高灵敏度以及易于集成等特点而得到了广泛的应用[1-3]。然而，由于硅基半导体具有热敏、负电阻率温度、掺杂等特性，因此硅基压阻式压力传感器极易受到温度等因素的影响，给测量结果带来误差[4]。另外，受掺杂、扩散等工艺水平的限制，压阻式压力传感器硅芯片上的电阻无法实现理论上的完全一致，造成了个体差异，且随着温度变化，这种差异会被放大。

压阻式压力传感器受温度影响具有以下三个特点。第一，由于半导体材料的热敏特性，传感器特性与工作温度变化具有相关性，随着温度变化，传感器输出的误差也在不断改变。第二，由于半导体材料存在的负电阻率温度特性，传感器输出结果与温度之间存在一定的非线性特性。第三，在传感器个体差异存在的情况下，温度和压力变化会放大这种差异，而且具有随机性和不确定性的特点。

目前，温度补偿主要有硬件补偿和软件补偿[5-7]。其中，硬件补偿是通过给检测系统增加附加电路，使系统产生与温度漂移值极性相反的信号以达到补偿的效果。这种补偿方法在一定程度上减小了温度引起的测量误差，但由于存在增大器件体积、增加设计难度以及复杂度等问题，在实际应用中受到了一定的局限。软件补偿方法是一种利用软件算法实现对硅基压阻式压力传感器温度效应进行校正和补偿的方法。由于不增加系统的硬件设备，且具有易修改、精度高等优点，因此相比于硬件补偿方法具有更好的应用和拓展性。目前常用的软件补偿方法主要有最小二乘法、神经网络等[8-9]，最小二乘法无法解决样本数量较多且具有随机性的回归问题，而神经网络存在泛化能力较弱，且过于依赖设计者经验的情况。

支持向量机(SVM)是一种建立在统计学理论基础之上的有监督学习算法，其严格的理论和数学基础有效的避免了经验成分的影响，具有很强的鲁棒性[10-12]。SVM对小样本的非线性数据回归效果好，能够契合压阻式压力传感器受温度影响的特点，是解决传感器输出准确度较低的有效方法。SVM在实际应用时核函数参数和惩罚参数取值困难，此时可以通过差分进化算法(DE)在给定范围内进行全局搜索，获得最佳参数[13]。

本文提出了一种基于DE-SVM的硅基压阻式压力传感器温度补偿模型，该算法能有效提高测量的准确度，并且适用于多传感器情况，改善由于测量环境和生产制造过程所导致的随机性误差。

1 基于DE-SVM的温度补偿方案

1.1 温度对半导体硅材料的影响

硅基压阻式压力传感器是利用集成电路工艺，在N型硅芯片上扩散等值P型电阻形成惠斯通电桥而制成。P型硅的电阻率为

式中:p为空穴浓度，q为电子电量，μp为空穴的迁移率。当给P型硅半导体材料在一定方向施加压力作用时，电阻率变为

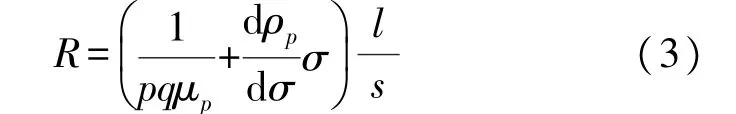
式中:l为半导体长度，s为半导体的截面积。

因此，硅基压阻式压力传感器的输出不仅与所受压力有关，而且与扩散电阻内部载流子浓度和迁移率有着密切的关系，在半导体内部不同散射机构的影响下，迁移率与温度的关系为

在低温下，电离杂质散射起主要作用，由声学波散射主导的AT3/2项忽略不计，载流子主要由杂质电离提供，此时杂质还未完全电离，随着温度T上升，p迅速增加。由式(5)可知，此时R随温度上升而减小。当温度升高到包括室温在内的中间温度区后，杂质已经全部电离，p基本不随温度变化，而声学波散射起主要作用，电离杂质散射主导的BNiT-3/2项忽略不计。因此随温度升高，R上升。当温度继续升高到高温区，本征激发产生大量载流子，远远超过晶格散射带来的的影响，此时R随温度升高快速下降，器件无法正常工作。

传感器内部硅芯片上的电阻一方面受压力影响，电阻率发生变化，从而改变扩散电阻的阻值；另一方面，由于硅材料的热敏和负电阻率温度特性，环境温度变化时，引起硅芯片中载流子迁移率改变，电阻率随之改变，使扩散电阻阻值发生变化。阻值的变化通过内部电路以电压的形式输出，读取电压信号则能够获得压力值。再加之工艺的影响，扩散电阻阻值存在一定的随机性误差，因此，压力传感器在这些因素的共同作用下，输出值必然存在着一定的误差。

1.2 补偿方案及机理

基于DE-SVM的硅基压阻式压力传感器温度补偿方案主要由训练数据预处理模块、DE参数寻优模块、SVM训练模块、数据采集模块、测量数据预处理模块以及SVM校正等模块组成，具体补偿方案结构如图1所示。

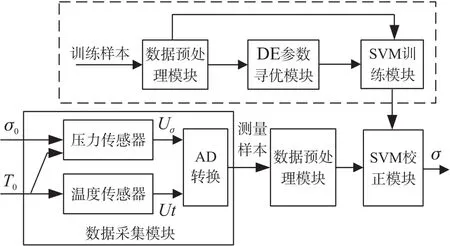
图1 基于DE-SVM的补偿方案结构图

如果设n为样本数目，σ0为实际压力值，xn为输入向量，且 xn＝[T，σt]，T 为环境温度值，σt为传感器输出的压力值，此时训练样本可表示为{(x1，σ01)，(x2，σ02)，…，(xn，σ0n)}。 对训练样本进行预处理，使其归一化至(-1，1)范围内，接着输入DE算法中寻找SVM算法的最优惩罚参数c和核函数参数γ。

在DE参数寻优过程中，给定种群的数量和进化代数，赋予个体两个属性值，c和 γ。其中 c与SVM拟合程度的调节有关，而γ来自于SVM核函数

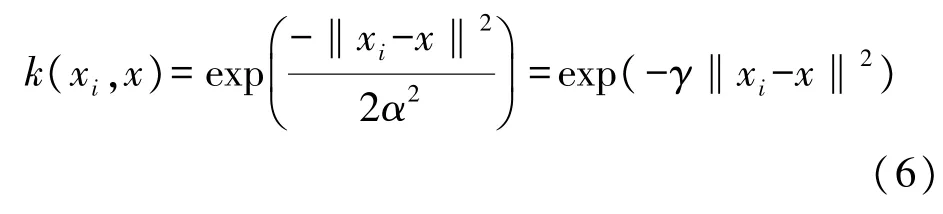
当DE参数寻优模块输出最佳参数赋值给SVM训练模块，SVM训练模块用训练样本训练完成最终的SVM校正模块。在测量过程中，数据采集模块中的传感器感知到环境压力值σ0和温度值T0后，会输出电压型模拟量Uσ、UT，并经过AD转换电路转换为数值量σs、Ts，构成测量样本。通过数据预处理后，输入SVM校正模块，最终输出校正后的压力值σ。

此时，测量压力值σs、校正后的压力值σ和测量温度值Ts满足

式中:反函数部分相当于回归方程，由SVM校正模块决定。

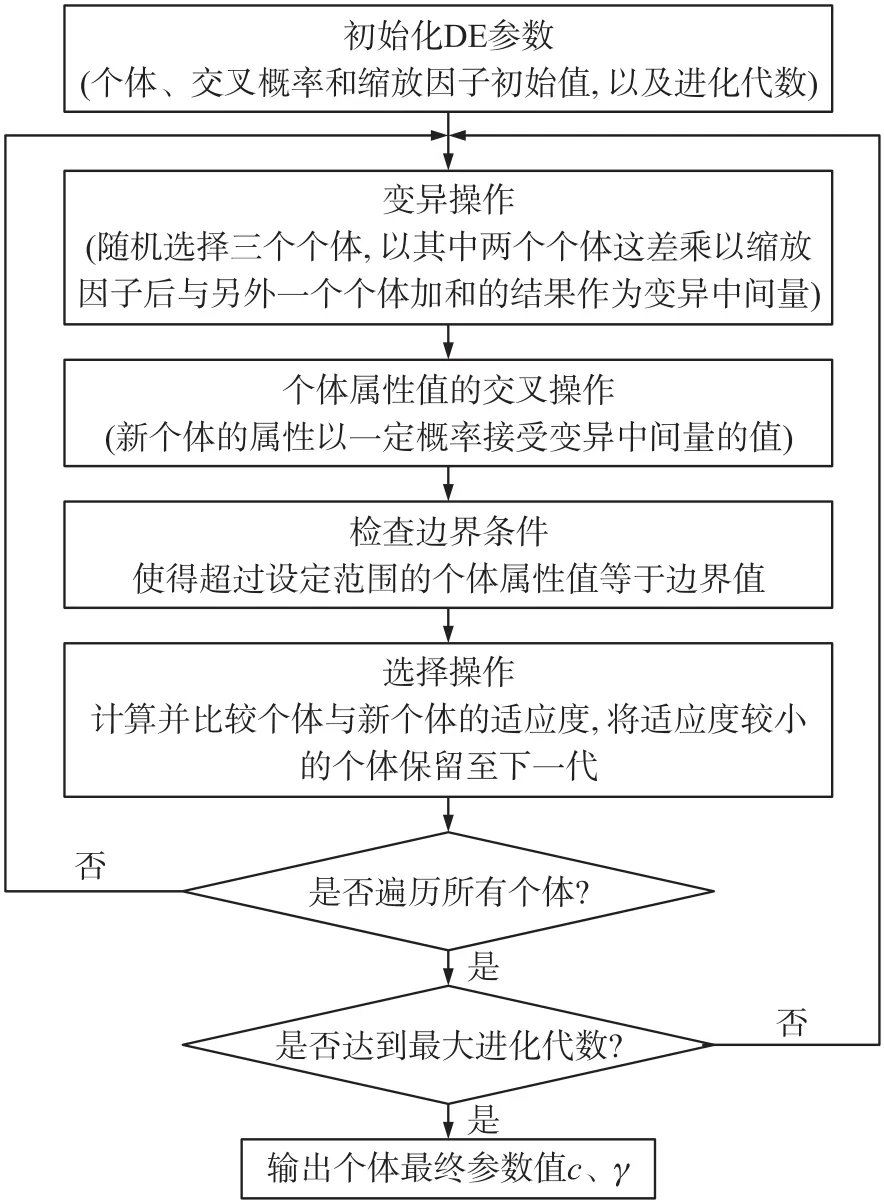
图2 DE算法流程

2 实验分析

实验选用的硅基压阻式压力传感器为表压型，测量范围为0～1.6 MPa，非线性误差为满量程的±0.15%，基准环境温度为25℃，工作温度范围为-40℃～125℃，基于项目需求仅对其中-10℃～80℃做温度补偿实验。

2.1 单传感器温度补偿实验

为了测试传感器输出与温度的关系，以单个传感器为测试对象，将其置于实验箱内。压力设置为0 MPa，分别在-10℃到80℃之间采集传感器的输出值，如图3所示。

由于硅片上扩散电阻在器件能够正常工作的温度范围下，阻值呈先下降后上升的趋势，经由传感器内部电路最终输出的压力值与扩散电阻阻值成反比。图3中温度由低到高变化过程中，传感器输出先上升后下降，呈非线性的特点，与理论分析相符合。

为了测试传感器输出与所受压力之间的关系，在上述实验的基础上，设置实验箱压力值0.8 MPa、1.6 MPa，获得的实验数据如图4所示。

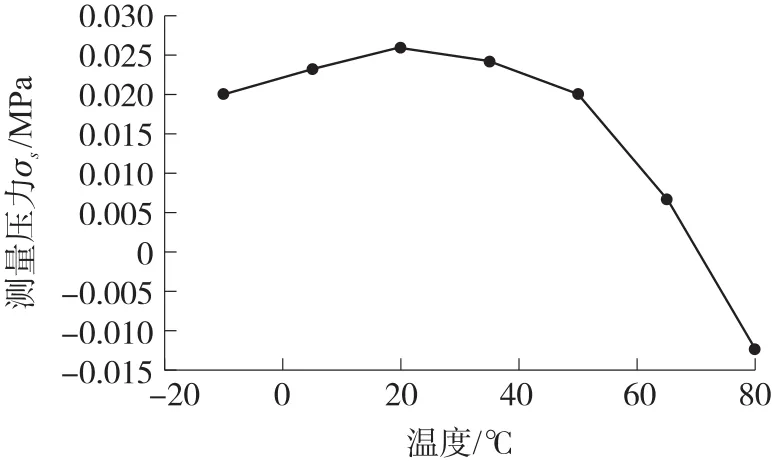
图3 常压下传感器在不同温度下的输出

图4 传感器在不同温度、压力下的输出

图4中传感器测量压力σs与被测压力σ0呈线性关系，与式(2)的结论吻合。同时，可以发现受温度影响，在不同温度下测量压力关于被测压力的折线没有重合，斜率也存在差别，最大误差大约为0.137 MPa，均方误差为 4.69×10-2MPa。

为了验证DE-SVM温度补偿方案在单个压力传感器测量数据上的补偿效果，根据所设计的温度补偿方案对图4中测量数据进行校正，其中，DE参数寻优模块初始化种群数量为10，进化代数为100。校正后的结果如图5所示。

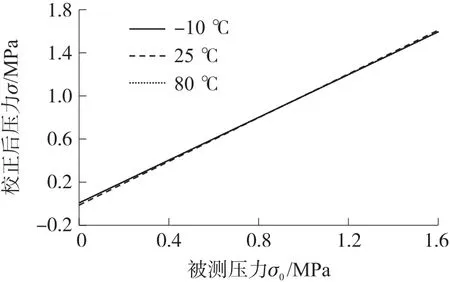
图5 校正后的值

校正后图5中的折线已基本重合，最大误差由0.137 MPa下降至8.40×10-3MPa，减小了93.87%；均方误差由4.69×10-2MPa下降至5.17×10-5MPa，减小了99.89%。

2.2 多传感器温度补偿实验

为了测试多个压力传感器在受温度和压力影响下表现出的个体差异，下面以七块传感器为测试对象进行实验。温度选择-10℃、25℃和80℃，压力选择0 MPa、0.8 MPa和1.6 MPa，分别测量并记录数据，如图6所示。

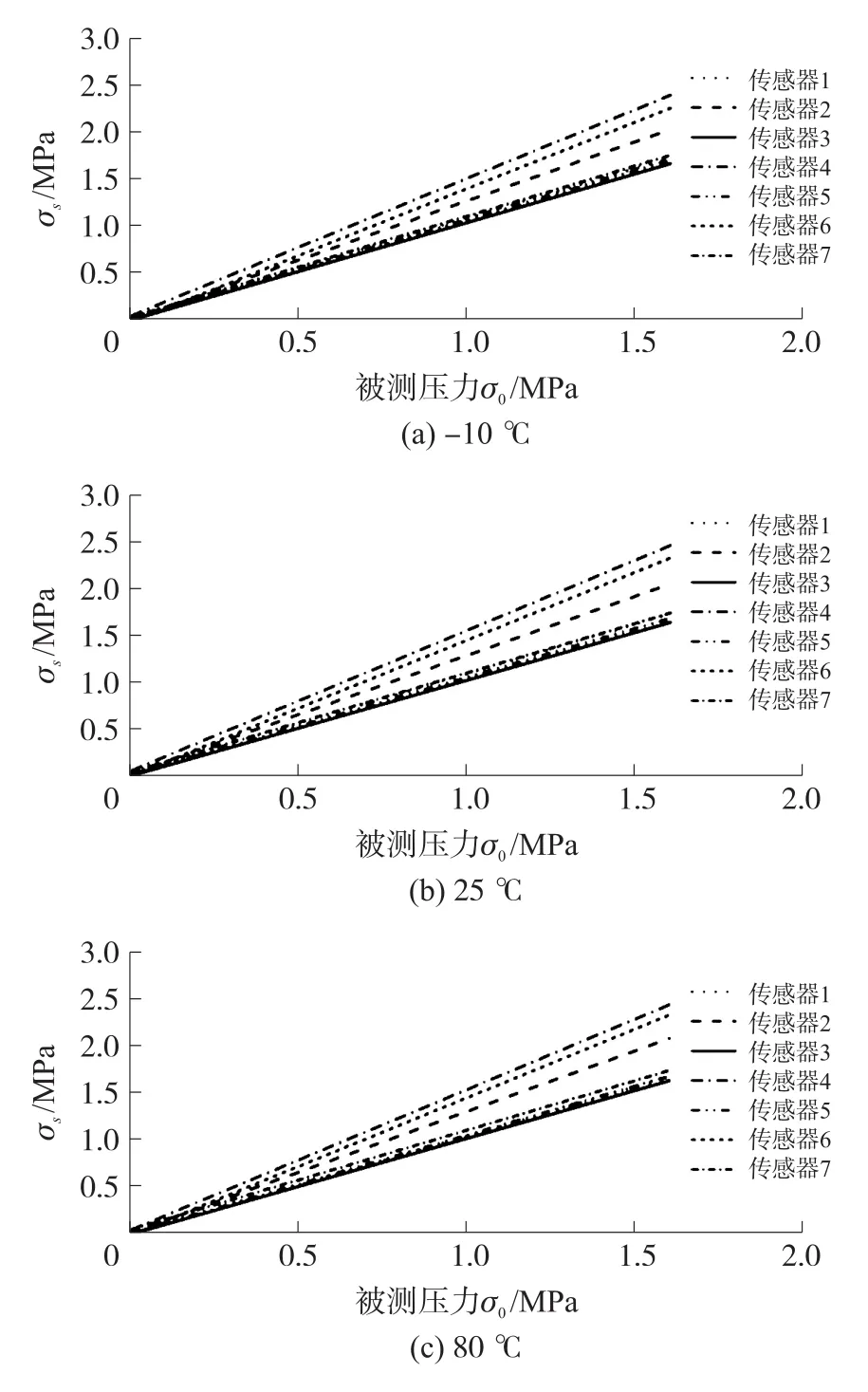
图6 多传感器在不同温度压力下的输出

由图6可以发现传感器在不同温度和压力下的输出均具有良好的线性度，但不同传感器的斜率差别较明显，将会导致随着被测压力的增加，测量值与准确值的偏移量增大的现象。实验中最大误差为0.874 MPa，均方误差为8.52×10-2MPa，平均相对误差达到了14.06%，零位输出的平均误差为1.83×10-2MPa，其零位温度系数α0和灵敏度温度系数αs分别满足

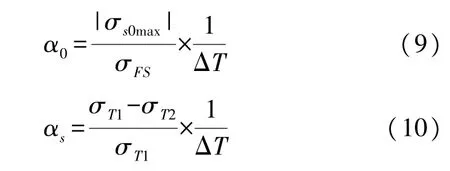
式中:ΔT为温度变化范围，σFS为满量程输出值，σs0max为最大零点漂移值，σT1-σT2为满量程下输出值随温度变化的最大改变量(σT1＞σT2)。经过计算，实验中 7个传感器的平均 α0和 αs分别为 1.31×10-4/℃和 3.03×10-4/℃。

为了测试DE-SVM温度补偿方案在多个压力传感器测量数据上的补偿效果，根据所设计的温度补偿方案对图6中测量数据进行校正，其中，DE参数寻优模块初始化参数不变。校正后的结果如图7所示。

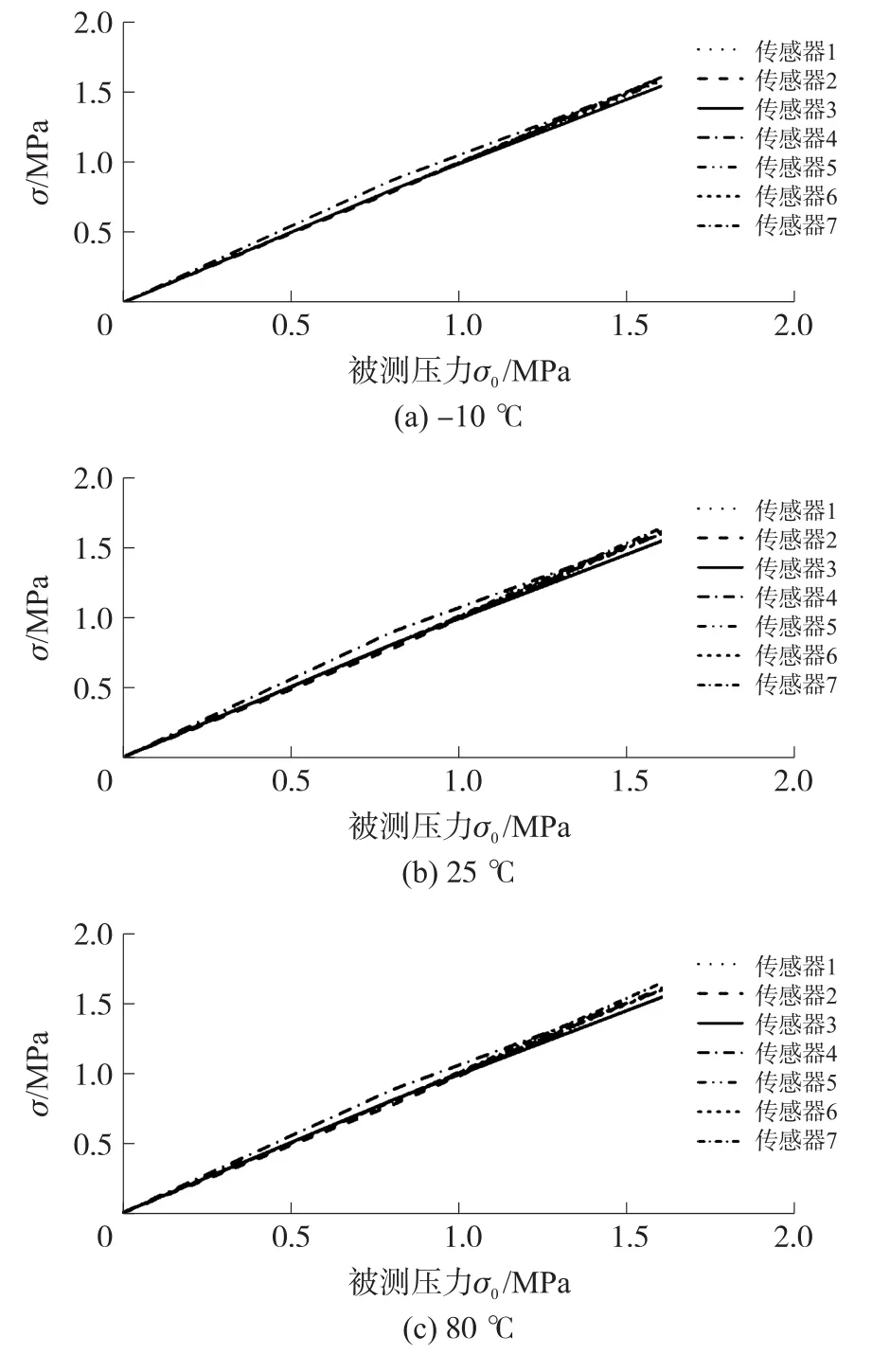
图7 多传感器校正后输出

与图6相比较，图7中七块传感器在不同温度下校正后的压力关于被测压力的折线的一致性得到了明显的改善，最大误差由0.874 MPa下降至5.97×10-2MPa，减小了93.17%，均方误差由8.52×10-2MPa下降至6.19×10-4MPa，减小了99.27%，平均相对误差下降至1.20%，此时零位输出的平均误差为6.7×10-3MPa，根据式(9)、式(10)计算得到平均 α0和 αs分别为 5.14×10-5/℃、7.15×10-5/℃。 因此，通过补偿前后的数据可以发现该温度补偿方案有效地提高了测量的准确度，并且较好地改善了温度稳定性。

2.3 任意温度点补偿性能验证实验

为了测试用三个温度点建立的DE-SVM温度补偿模型在其余温度点的表现情况，温度选择15℃和40℃，压力选择0 MPa、0.8 MPa和1.6 MPa，对7块传感器分别测量并记录数据，如图8所示。

图8 测试点温度校正前输出

经分析计算，40℃时测量数据的平均相对误差为15.01%，均方误差为9.44×10-2MPa。15℃时测量数据的平均相对误差为14.86%，均方误差为9.06×10-2MPa，二者零位输出的平均误差为0.014 MPa。将数据输入之前建立的DE-SVM模型内进行校正，校正结果如图9所示。

图9 测试点温度校正后输出

经过校正，40℃时的平均相对误差下降至1.36%，均方误差下降至 8.85×10-4MPa，减小了99.06%。15℃时的平均相对误差下降至1.31%，均方误差降至7.91×10-4MPa，减小了99.13%，二者零位输出的平均误差降至6.7×10-3MPa。由此可见，三温度点建立的DE-SVM模型适用于其余温度点的温度补偿，并取得了较好的效果。

3 结论

本文提出一种基于DE-SVM的压力传感器温度补偿方案，传感器采集的压力数据经过补偿，可以将环境温度造成的影响在一定程度上加以校正。经实验表明，DE-SVM温度补偿方案能明显降低压力传感器在温度影响下的测量误差，并且在多传感器情况下能够有效改善传感器之间的个体差异。