独立不同分布不确定变量中心极限定理证明及其应用
孟祥飞,王 瑛,李 超,亓 尧,孙 贇
(空军工程大学 装备管理与无人机工程学院,西安 710051)
在对实际问题进行建模时,经常遇到研究对象处于动态复杂环境中的问题,导致所构建模型中的参数难以确定,此现象称为非决定性现象.非决定性现象主要分为两类:① 随机现象,即有大量样本数据的非决定现象;② 带有专家信度的现象,即样本数据非常少或无法得到样本数据而只能依靠专家经验作出判断的现象.
通常采用概率论理论与方法解决随机型的非决定现象,而采用不确定理论解决带有专家信度的非决定现象.解决非决定现象最重要的工作是确定随机变量或不确定变量的分布函数.对于简单的分布函数,一般可用最小二乘法、矩估计法和Delphi法等[1-2].但是对于一些特殊情况,上述方法则不再适用.例如,现实中有很多随机变量是由大量随机因素共同作用而形成的,且每个因素所起到的作用较小,即并非某一个因素起到决定性的作用.为解决这种多种随机因素作用的问题,法国数学家棣莫弗和拉普拉斯首先提出了中心极限定理并给出了证明[3-4].林德贝格、李雅普诺夫及马尔科夫等对该定理进行了更深入的研究.中心极限定理表明,这种随机变量服从的概率分布往往会收敛到一类共同分布,即正态分布.同时,该定理提供了一种近似确定独立随机变量之和分布的近似方法[5].
目前,不确定理论中尚未提出中心极限定理.因此,尚无较好的处理多不确定因素共同作用问题的方法.文献[6]所构建的不确定多目标规划模型将部件的修复率和故障率等参数作为不确定变量,解决了数据缺失条件下可修复系统的冗余分配问题.文献[7-8] 所建模型将交易价格、供应量和需求量作为不确定变量,讨论了不确定环境下多目标股票交易问题.此外,因雷暴等恶劣天气造成航班延误,在处理航班延误的恢复问题时,航班重新出发的时间是一个多因素共同作用的不确定变量问题.在天气好转之前,航班可能无法恢复,而当天气达到起飞或降落条件之后,空管部门可能会对空中交通流量实施管控,导致延误航班仍停留在机场无法执行任务.而飞机机械故障、乘客原因以及机组失误等原因共同造成的航班延误更加难以恢复,签派员只能根据经验进行适当调整[9-11].又如,新型坦克的射击精度受到坦克行驶速度、路面状况、车载武器系统和瞄准系统的小规模震动、底盘线震动以及坦克内部的空间结构设计等因素的影响,凭经验很难估计坦克多次射击的结果.大量文献中不确定变量是受诸多不确定因素的影响[12-18],为简化计算,这些研究直接给定不确定变量分布或根据经验数据拟合其分布,而难以描述多不确定因素对事件所造成的影响.
基于此,本文主要研究不确定理论中的中心极限定理.首先,定义不确定分布的特征函数并分析该定理具有的部分性质.其次,将概率论中的正态分布引入到不确定理论中,提出两个中心极限定理并予以证明.
1 不确定变量特征函数定义及其性质
本文借鉴概率论中随机变量特征函数的概念,提出不确定变量的特征函数.
定义1设ξ为不确定变量,则对于任意实数x,函数Φ(x)=M{ξ≤x}为ξ的不确定分布,M{ξ≤x}为测度函数.
定义2函数Φ(x)为一个正则不确定分布,当且仅当其为一个不满足Φ(x)≡1或Φ(x)≡0的严格单调递增函数.
定义3设ξ是一个不确定变量且服从正则不确定分布,则记Φ(x)的反函数Φ-1(α)为不确定变量ξ的不确定逆分布.其中α为信度,0≤α≤1.
定义4对于ξ,其期望值为
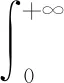

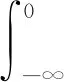
定义5ξ服从正则不确定分布Φ(x),则称φ(t)为Φ(x)或ξ的特征函数,φ(t)=E(eitξ),-∞ 根据定义4,Φ(x)或ξ的特征函数可表示为 (1) 由此可见,不确定变量的特征函数取决于其服从的分布函数,若分布函数相同则特征函数必定相同.ξ的特征函数具有以下性质: 性质1对于任意t,有|φ(t)|≤φ(0)=1. 证明根据欧拉公式可得: 性质2ξ,η为不确定变量,若ξ与η相互独立,则φξ+η(t)=φξ(t)φη(t). 证明根据文献[16],eitξ和eitη为不确定变量且相互独立,于是有 φξ+η(t)=E[eit(ξ+η)]= E(eitξeitη)=E(eitξ)E(eitη)= φξ(t)φη(t) 性质3ξ服从正则不确定分布,其特征函数在(-∞,+∞)上一致连续. 证明对于任意实数t,h,a(0 |φ(t+h)-φ(t)|= 根据性质1,有 |eihΦ-1(α)-1|= 对任意t∈(-∞,+∞),有 即φ(t)在R在一致连续. 证明对于a≥0,根据性质1,有 对于a<0,有 |eia-1|= |eia(ei|a|-1)|≤|eia||ei|a|-1|≤ |ei|a|-1|≤|a| 对于任意a,有 |eia-1|≤|a| (2) 于是 |i||e-itx1||1-e-it(x2-x1)|≤x2-x1 证明根据特征函数的定义有 根据性质3及4,交换积分次序,有 由狄利克雷积分,可知 记 S(T,x,x1,x2)= 则 因此必存在O>0,使得|S(T,x,x1,x2)| 其中:ν为充分小的正数.则有 性质6ξ服从正则不确定分布函数,其特征函数唯一确定. 证明由性质3及5可得 (3) 由式(2)可得 (4) (5) 根据性质5,对Φ(x)上每一个连续点x,当y沿着Φ(x)的连续点趋于-∞时,有 (6) 综合考虑式(5)及(6),可知不确定分布函数在任意x处的取值由其连续点上的值x及其特征函数决定,即不确定分布函数具有唯一确定的特征函数. 证明对Φ(x)求导可得 即Φ(x)关于x单调递增,并且Φ(x)在x∈(-∞,+∞)上连续. 式中:r和θ为极坐标参数,均为正实数. 综上所述,Φ(x)为正则不确定分布函数,记为G(μ,σ2)分布. 则对任意实数x,有 证明根据式(2)可知|eia-1|≤|a|. 当a=0时有 |eia-1-ia|=|1-1|=0≤a2/2 当a>0时有 |eia-1-ia|= (7) 式中:o(x)为x的高阶无穷小. 同理 当a<0时,有 综上,对于任意的实数a,有 (8) (9) (10) (11) 根据式(10)及(11),有 (12) 根据积分运算法则,有 (13) 进一步简化,得 于是林德贝格条件转化为:∀τ>0,有 (14) 即在式(14)的条件下证明 (15) 则有 (16) 根据式(10),有 (17) 根据式(8),式(17)可化为 (18) 其中:1≤i≤n. 根据式(18)可知,∀t∈[-T,T],有 则有 (19) 当n充分大时,根据式(19)有 (20) 由式(20)可知存在正整数M,当n≥M时有 (21) 因此,在任意区间[-T,T],式(16)可展开为 (22) 由式(21)可得 由式(12)及(18)可得 (23) (24) 由式(2)及(8)可得 (25) 当τ足够小时,必存在正实数ρ,使得 式(25)可化为 由式(12)可知,∀t∈[-T,T],有 由式(14)林德贝尔条件,存在正整数A及对应的ρ>0,当n≥A时,有 于是,∀t∈[-T,T],有 |Γn(t)|<λ (26) 根据式(26),当λ取足够小的正实数时,有 于是式(24)转化为 (27) 根据定理1,有 则对任意实数x,有 (28) 必存在实数κ>0及足够小的正实数τ使得 根据不确定变量k阶矩计算公式有 (29) 根据式(29)有 (30) 根据式(28)及式(30)有 根据定理3有 新型坦克在装备之前需经过多次射击进行测试,某场测试中,按难易程度共设置10种标靶,每种标靶的数量为1. 记事件γi1为该坦克命中第i种标靶,事件γi0为该坦克未命中第i种标靶.定义不确定变量ξi如下: ξi的方差为 M(γi1)-(γi1)2=M(γi1)(1-γi1)= 易知从ξ11开始的不确定变量都与ξ10同分布且相互独立.当κ=1时,验证不确定变量序列{ξn}满足李雅普诺夫条件,有 M(γi1)M(γi0)3≤M(γi1)M(γi0) 于是有 即{ξn}满足李雅普诺夫条件,可以使用定理3. 又因为 所以该坦克通过测试的信度为 1-Φ(0.362 7)=1-0.640 6=0.359 4 由此看出,该坦克通过测试的信度约为0.36,信度较低.坦克射击精度测试需对不同类型的标靶进行瞄准射击,测试的总成绩与每一次射击结果密切相关,而且坦克的射击精度受自身性能及外部环境等不确定因素的影响,若专家根据经验无法对坦克通过测试这一事件进行较准确的估计.因此,在处理该问题时,首先需利用不确定中心极限定理确定坦克通过测试这一事件服从的不确定分布,然后再进行分析计算. 本文针对独立不同分布的不确定变量提出中心极限定理.首先定义了不确定分布的特征函数并给出了计算法则.然后将随机理论中的正态分布引入到不确定理论并证明该分布的函数形式可以作为一个不确定分布.在此基础上,提出了两个独立不同分布的不确定中心极限定理,可为不确定理论在现实问题中的应用起到一定的促进作用.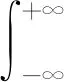







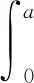



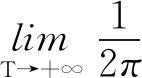
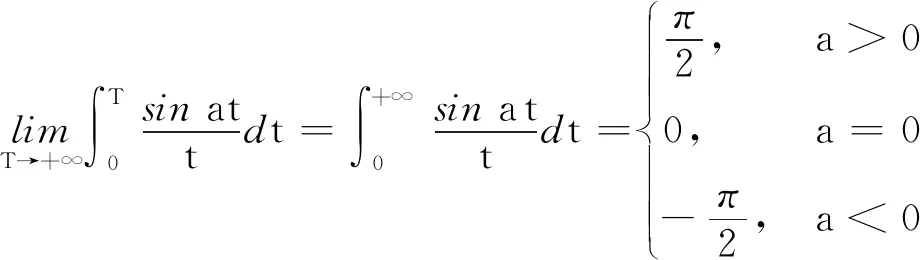
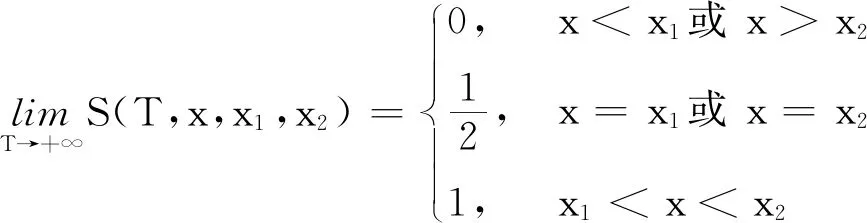
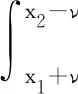
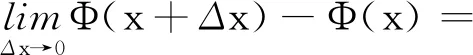

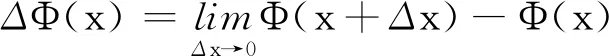
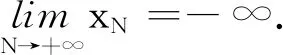
2 独立不同分布不确定中心极限定理

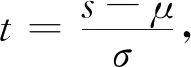
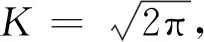
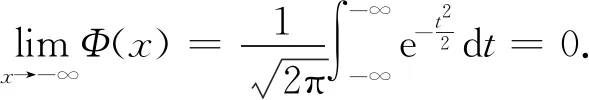
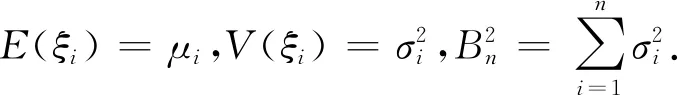
|eia-1-ia+a2/2|=
|1-1|=0≤a3/6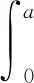
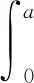

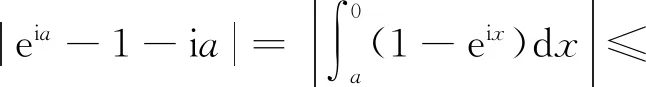
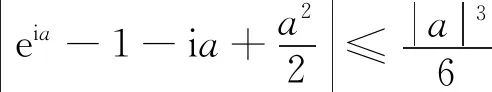
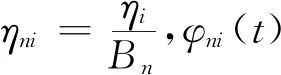
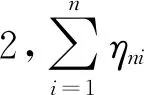

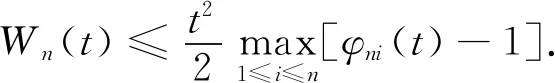

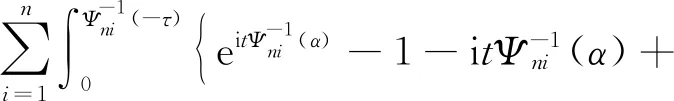

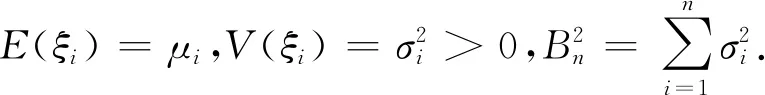

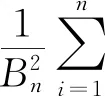

3 案例分析
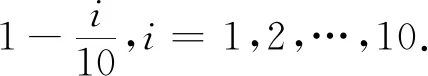




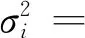
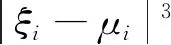
4 结语

