基于Hermite组合核EMD-WT-LSSVM的非平稳非高斯风压预测

李春祥，裴杨从琪，殷 潇

(上海大学 土木工程系，上海 200444)

风荷载是高层、大跨结构建筑的主要设计荷载，掌握风场特性对于大跨结构抗风设计具有的重要意义.随着统计理论与机器学习的快速发展，最小二乘支持向量机(Least Square Support Vector Machine,LSSVM)在解决小样本、非线性及高维数问题中表现出泛化能力强、训练速度快以及全局优化等优点.因此，众多学者采用该方法预测结构风场的数据，利用已知的有限风压时程样本的特征信息进行训练学习，再泛化外推获得未知的风压时程样本息[1-2].

现有的风特性分析方法通常假定风荷载为平稳高斯随机过程.而已有的实测资料表明，复杂地形条件或强风场下，气流容易发生较强的分离或旋涡运动.因此，风荷载通常表现出明显的非平稳性，结构表面风压概率分布呈现出强烈的非高斯随机特征[3-5].该情况下，采用平稳高斯模型进行抗风设计将会导致较大的分析误差.本文将经验模态分解(Empirical Mode Decomposition,EMD)与LSSVM结合，将实测风压分解并通过具备良好时频特性的小波变化(Wavelet Transform,WT)算法对分解所得的固有模态函数进行去噪.将去噪后的固有模态函数及剩余分量输入最小二乘支持向量机进行训练学习并预测重构出所需的风压时程.

1 EMD-WT-LSSVM

1.1 EMD基本理论

经验模态分解法是1种适用于非线性非平稳信号的新型自适应信号时频处理方法.该方法将信号分解为少量满足以下条件的固有模态函数(Intrinsic Mode Functions,IMF)：① 在整个数据集中，极值点的个数与穿零点的个数相等或两数最大差值为1；②在任一点，由所有极大、极小值点形成的包络均值为0.通过筛分过程将IMF分解，直至剩余分量(Rn)很小或为1个单调函数.事实上，经过多次筛分后，剩余分量周期大于样本持时，信号频率较低，可视为时变平均风压成分，则非平稳风压时程P(t)可表示为

(1)

式中：n为分解序列数，N为总分解序列数.

1.2 小波去噪

小波理论具备良好的时频特性，在信号去噪中得到了广泛应用并取得了良好的效果[7-8].高斯白噪声在时间域没有连续性，因此经过小波变换后表现出很强的随机性，而有效信号经小波分解后小波系数较大，选取1个合适的阀值，大于阀值的小波系数可认为是有效信号产生的，应予以保留，小于阀值的小波系数则认为是噪声产生的，将其置为0以达到去噪的目的.小波去噪的基本步骤包括信号的小波分解、高频系数的阈值量化及信号的小波重构.本文选用db4小波母函数对各IMF信号进行两层分解并提取系数，获取各频段阈值，并进行软阈值处理.

1.3 LSSVM

给定一组训练样本集：T={(xi,yi)|xi∈Rn,yi∈R,i=1,2,…,N} ，其中xi为n维输入向量的元素，yi为对应的训练样本输出值，N为样本数.LSSVM利用非线性映射将样本由输入空间映射到高维特征空间，进一步寻找特征空间的线性关系以实现输入空间的非线性处理，其线性回归方程为

y(x)=ωTφ(x)+b

(2)

式中：φ(x)为非线性变换映射函数；ω为权向量；b为偏置量.基于SRM原则，LSSVM的目标优化函数可描述为

(3)

式中：γ为正则化参数；ei为松弛因子，且式(3)满足yi=ωTφ(xi)+b+ei.引入Lagrange乘数法求解函数的最小值：

(4)

式中：αi为Lagrange乘子.对(4)式求偏导：

(5)

消除式(5)中的ω和ei得

(6)

(7)

1.4 Hermite核函数及其组合核

由式(7)可知，核函数作为LSSVM预测算法的核心，其类型直接影响回归模型的预测性能.因此，解决实际问题时，核函数的选取尤其重要.高斯核函数(Radial Basis Function,RBF)具备良好的学习性能，在模式识别及回归预测等问题中被广泛运用且取得了较好的效果[9-10]，其表达式为

(8)

式中：σ为核宽度.

Hermite多项式满足以下递推条件：

(9)

对于给定的权函数ω(x)=e-x2，Hermite多项式序列为正交序列，即当m≠n时，有：

(10)

对于非零向量x，上限为k时的Hermite核函数为[11]

(11)

∬X×XK(x,xi)f(x)f(xi)dxdxi=

(12)

式中：X为任意的积分区域.可见，Hermite核函数为LSSVM允许核函数.

n过大时，预测模型的计算量较大，由式(11)可得一阶Hermite核函数为

K(x,xi)=1+4(x·xi)

(13)

可见，一阶Hermite核函数为全局核函数，该函数的泛化能力强而学习性能较弱，因而将其与典型的局部RBF组合，使得组合核函数兼具局部核函数在小范围内的强拟合性与全局核函数在整个数据集中良好的外推能力，组合核函数为

K(x,xi)=

(14)

式中：g∈(0,1).

支持向量机核函数理论在完备的内积空间中进行讨论，线性加法在希尔伯特空间属于封闭运算，根据Mercer核条件，核函数的线性组合仍为支持向量机允许核函数.本文采用的3种核函数及核参数的范围见表1.

表1 3种模型核函数及参数范围Tab.1 Kernel function expressions and spans of parameters of three models

2 实测风压数据及预测模型

对膜结构表面进行风压实测研究，可为膜结构设计提供依据，同时确保了膜结构体系的安全[12].现对某体育中心膜结构的表面整体风压进行风振实测研究，膜表面风压测点布置如图1所示，图中红圈内风压测点三维布置详图如图2所示.每个测点的上、下位置分别安装了风压传感器，以同步监测膜上下表面的风压时程.风压数据采样频率为100 Hz，最大风速为11.59 m/s，风力等级达到6级，属于强风级别.本文选取1、8和13测点实测风压数据稳定后500 s 内的 1 000 个数据点风压作为单点及空间点预测样本数据.实测风压与经EMD分解及小波去噪重构后的风压(p)信号如图3所示.

由图3可见，EMD-WT方法保留了实测风压序列的基本特征，消除了陡峭的极值，使重构后的风压序列稳定性得到较大提升.运用增广的迪基-福勒(Augmented Dickey-Fuller，ADF)检验法检验时间序列的平稳性.ADF检验表中不同置信水平(一般为1%、5%、10%)的临界值分别为-2.567、-1.941以及-1.616，若测点风压样本ADF值大于上述临界值，则表示该测点时间序列为非平稳时间序列.

表2所示为1、8和13测点的ADF检验值，可以看出，3个测点处风压样本的检验值均大于临界值，均为非平稳时间序列，结合偏度(S)及峰度(K)见表3.由表3可知，3测点处风压为典型的非平稳非高斯时间序列.

文献[13-14]首先将粒子群算法(Particle Swarm Optimization，PSO)应用于人工模拟鸟群的觅食行为，通过协同和竞争寻求粒子的最佳空间位置.采用粒子群算法对LSSVM正则化参数及表1中的核参数进行参数寻优，γ∈[10-2,103]，种群规模为30，最大迭代次数为150.以Hermite组合核函数为例进行单点预测说明，其流程如图4所示.首先，运用EMD将实测风压序列分解为一系列相对平稳的固有模态函数和1个剩余分量；其次，使用小波变换对每个固有模态函数进行去噪，将去噪后的固有模态函数及剩余分量作为样本输入，建立基于Hermit核函数及组合核的 PSO-LSSVM 的风压预测算法得到预测风压；最后，引入评价指标进行客观评价分析.

图1 风压测点布置平面图Fig.1 Wind pressure measuring points

表2 测点处ADF检验值Tab.2 Test value by ADF at measuring points

表3 测点处风压的峰度和偏度Tab.3 Skewness and kurtosis of wind pressure at measuring points

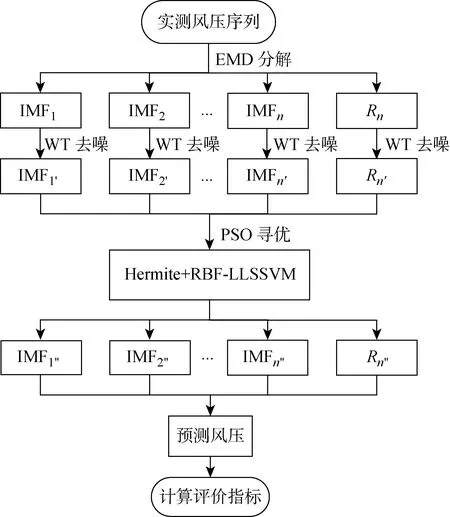
图4 单点风压预测流程图Fig.4 Flowchart of single point pressure prediction

图5 1测点预测风压及实际风压时程图对比Fig.5 Prediction of wind pressure and actual wind pressure time history diagram at Measuring Point 1

3 基于实测风压的预测算法验证

3.1 单点预测和鲁棒性验证

单点预测将EMD分解及小波去噪后的各IMF及Rn分为训练集和预测集2部分，嵌入维度取10，则训练集为490个10维向量，测试集为500个10维向量.将训练集输入LSSVM，构造出确定的输入输出关系，从而建立LSSVM风压预测模型.将预测模型应用到预测集，分别使用3种预测模型对各IMF函数及Rn后250 s的风压时程进行预测，将各分量预测结果叠加，得到1测点风压序列的后250 s非平稳风压，预测结果如图5所示.可以看出，3种模型的单点风压预测结果较好，其中Hermite混合核模型较其余2种模型的单点风压预测结果与实际风压更为吻合，走向与实际风压一致；而Hermite-LSSVM 的预测风压吻合程度明显优于RBF-LSSVM 但较混合核模型仍有差距.此外，RBF核函数为典型的局部核函数，具有较强的学习能力，但泛化能力差，易限于局部最优解.因此，在风压脉动性强的极值处，RBF-LSSVM的预测值与实际风压有较大误差.Hermite核函数为全局核，在整个数据集内具有良好的外推能力但对信号的局部拟合能力较弱，而组合核函数兼具全局核的泛化能力与局部核的学习能力，拟合性能更优.

图6为1测点自相关函数对比图.可以看出：组合核模型的脉动风压与实际风压脉动值的自相关性(M)比RBF-LSSVM与Hermite-LSSVM算法更高.图7为1测点的脉动风压功率谱(N)函数对比图.可以看出，该实际风压中低频成分幅值较大，同时混合核预测模型在低频和高频段与实际风压均更为接近，能更好地反映风压场能量分布，进一步验证此模型的良好预测性能.

图6 1测点预测风压及实际风压自相关函数对比Fig.6 Comparison of predicted wind pressure and actual wind pressure autocorrelation function at Mea-suring Point 1

图7 1测点预测风压及实际风压功率谱对比Fig.7 Comparison of predicted wind pressure and actual wind pressure power spectrum at Measuring Point 1

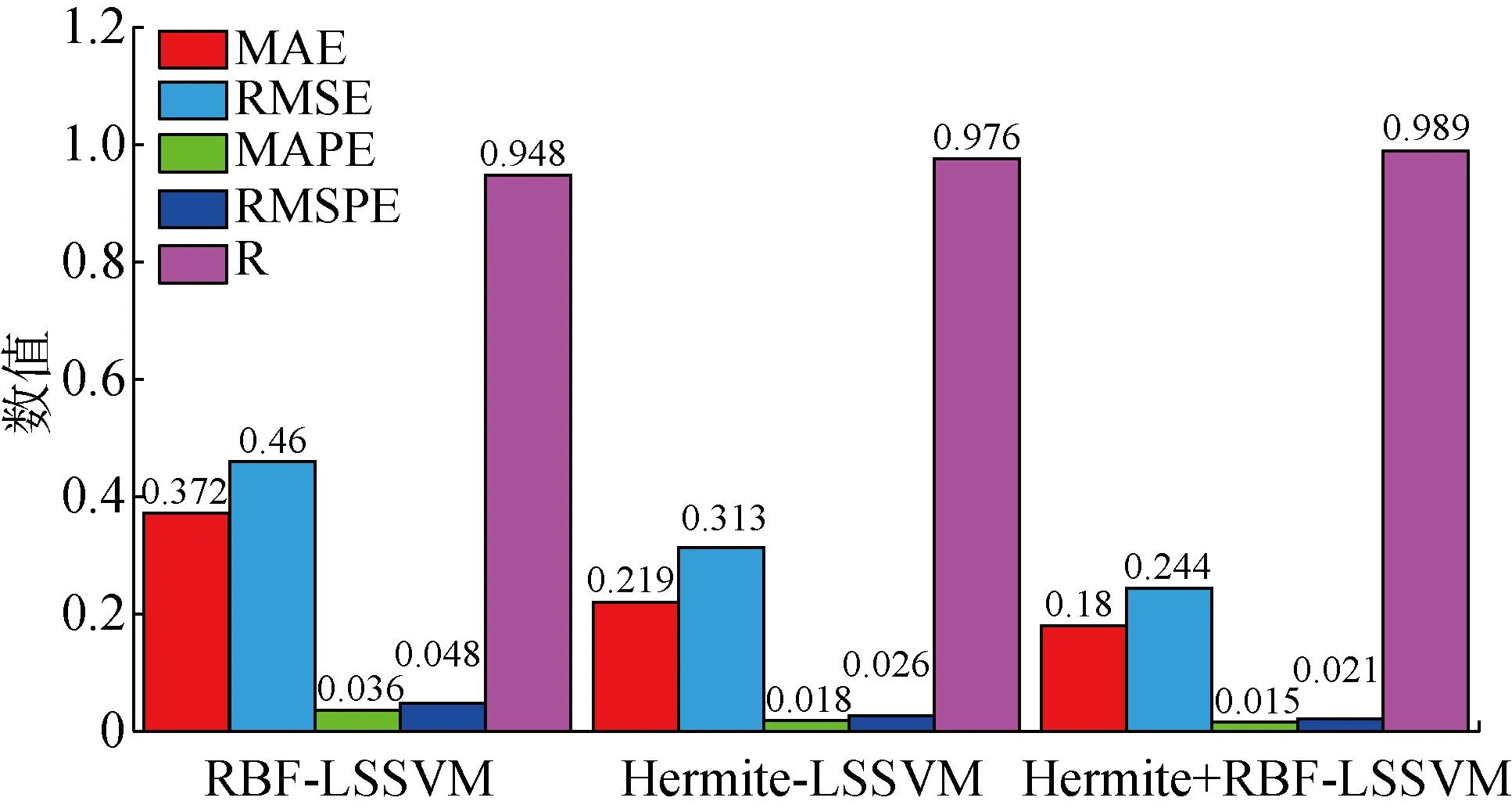
图8 3种预测算法的预测性能评价指标对比Fig.8 Prediction performance indexes of three predicting algorithms

可以看出，Herinte+RBF-LSSVM模型的预测精度最高，性能最优，相较于RBF-LSSVM模型，其MAE和RMSE值分别降低51.6%和47.0%，MAPE和RMSPE值分别降低58.3%和56.3%；较Hermite-LSSVM模型，其MAE、RMSE、MAPE和RMSPE也有不同程度的降低.3种模型的R值均大于0.9且Herinte+RBF-LSSVM模型的R值最大，表明其预测风压与实际风压的相关性最强.RBF-LSSVM、Hermite-LSSVM及Hermite+RBF-LSSVM 3种算法分别耗时273，324，358 s.未明显延长时间消耗的前提下，Hermite+RBF-LSSVM 模型的单点风压预测结果与实际风压之间误差最小，相关系数最高，可实现对单点风压更高精度的预测，为风工程计算分析提供更准确的风压时程.

为验证预测模型的鲁棒性，对青岛西海岸的青岛泽润广场超高层实测风压进行预测.该建筑距离海边大约3 km，场地粗糙度为A类.主楼为28层办公楼，建筑总高度为113 m.主楼结构采用框架-剪力墙结构体系，平面布置呈长方形，长和宽分别为43.6和21.3 m.

图9 风压传感器布置平面图(mm)Fig.9 Layout plan of wind pressure sensor (mm)

对该建筑进行了3面6点的风压现场实测.为了获得在强台风作用下超高层建筑的风压特性，6个风压传感器(wps1-wps6)的布置如图9所示，风向切入夹角为α.6个风压传感器模拟信号通过10 Hz低通抗混滤波器进入A/D转换采集卡，采用20 Hz采样率进行数据采集.

对6个测点时长500 s的实测风压时间序列进行降采样，降采样因子为10，利用3种预测模型分别预测6个测点时间采样序列后250 s的风压.经EMD分解及小波去噪重构后的风压信号如图10所示.表4为两个测点处的ADF检测值.可以看出，两个测点处风压样本检验值均大于临界值，故风压样本时间序列为非平稳时间序列.1，2测点的S及K值见表5.从表5可知，1，2测点风压样本为典型的非平稳非高斯随机过程.

图10 风压样本时程图Fig.10 Time history of wind pressure samples

图11～13分别为Hermite+RBF-LSSVM 的风压时程曲线、自相关曲线及功率谱曲线.可以看出，Hermite+RBF-LSSVM较其余两种模型的预测结果更接近实测风压，与实测结果吻合度最高.

表6为3种预测算法的预测性能评价指标对比，混合核模型预测精度最高，误差最小，在不同测点处均保持较高的预测性能.

表4 测点处ADF检验值Tab.4 Test value by ADF at measuring points

表5 测点处风压的峰度和偏度Tab.5 Skewness and kurtosis of wind pressure at measuring points

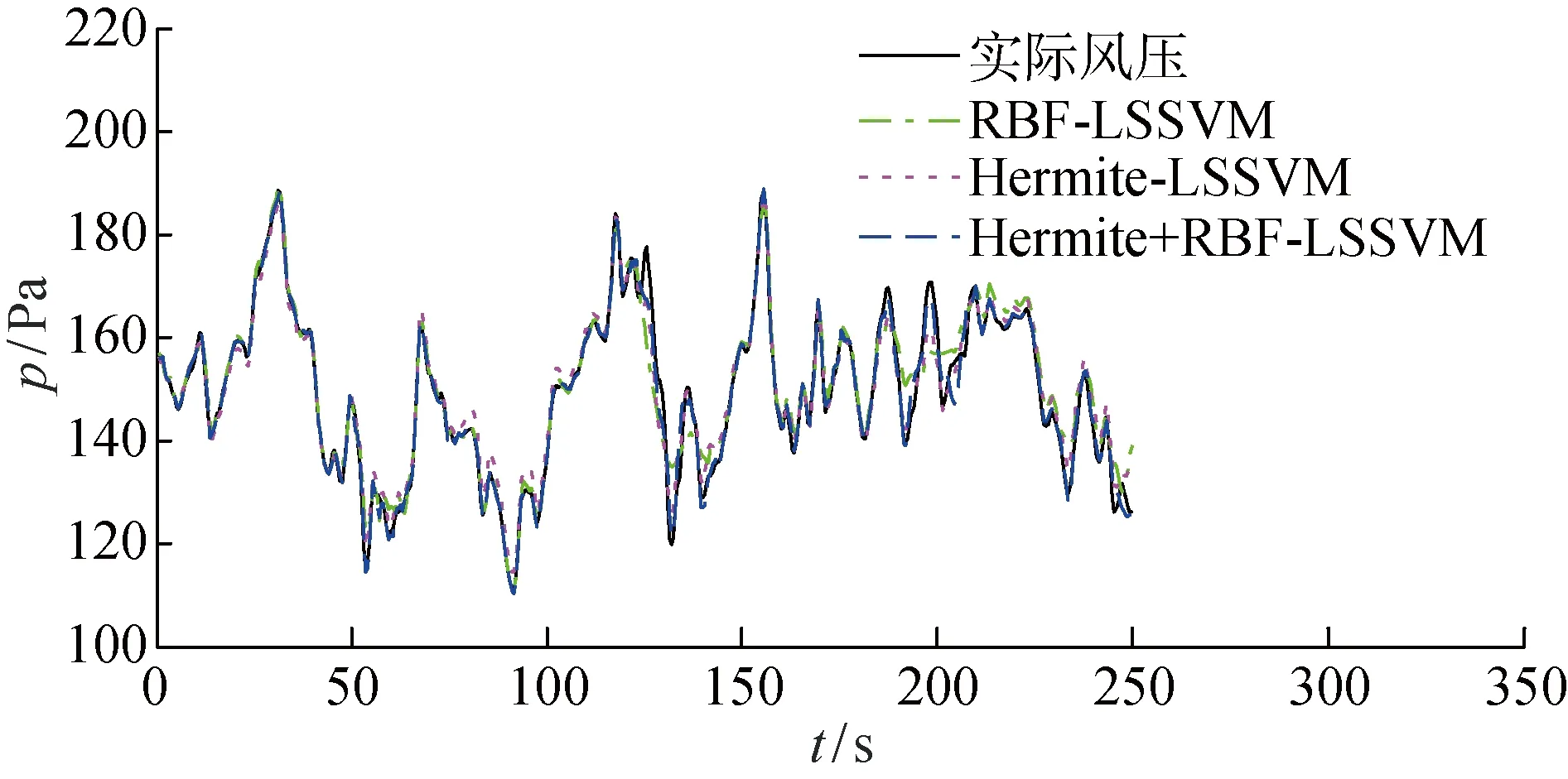
图11 预测风压及实际风压时程图对比Fig.11 Prediction of wind pressure and wind pressure time history diagram

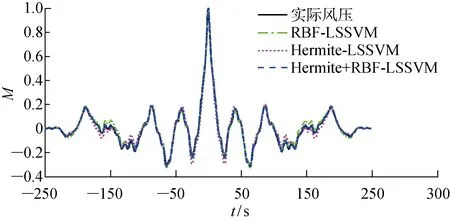
图12 预测风压及实际风压自相关函数对比Fig.12 Comparison of predicted wind pressure and actual wind pressure autocorrelation function

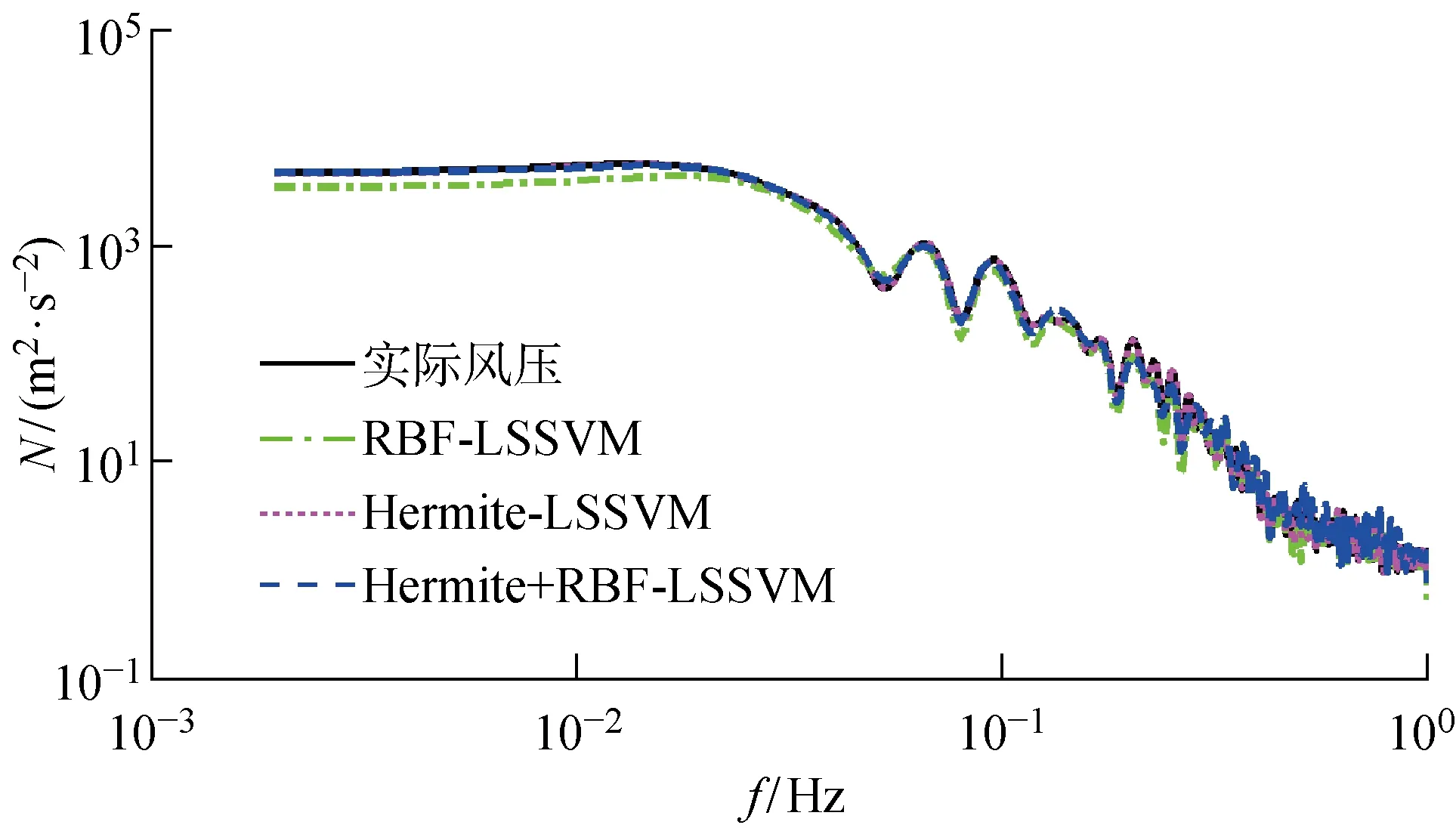
图13 预测风压及实际风压功率谱对比Fig.13 Comparison of predicted wind pressure and actual wind pressure power spectrum

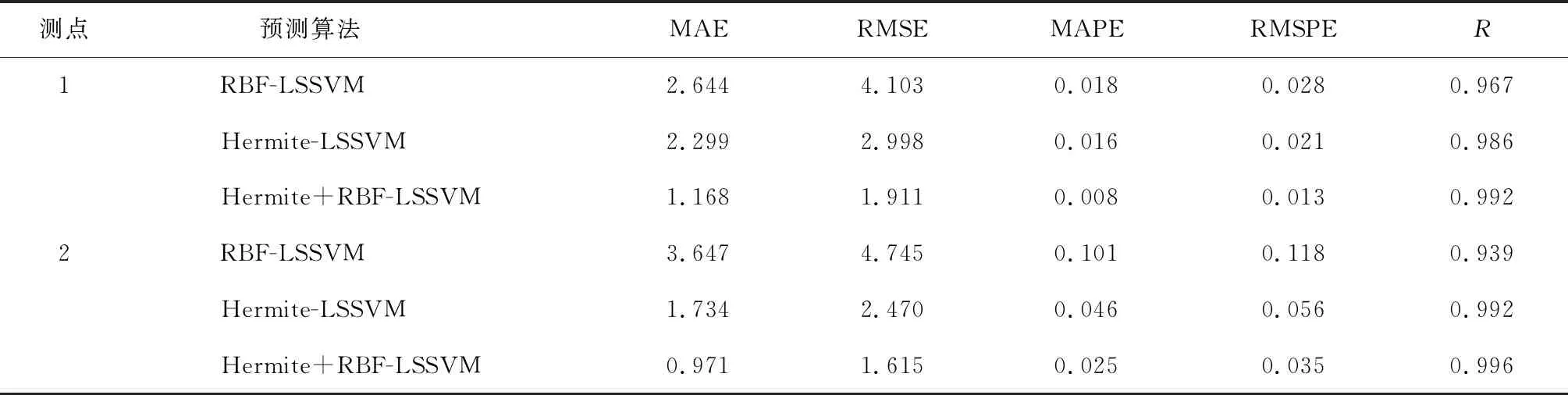
表6 3种预测算法的预测性能评价指标对比Tab.6 Prediction performance indexes of three predicting algorithms

3.2 空间点预测

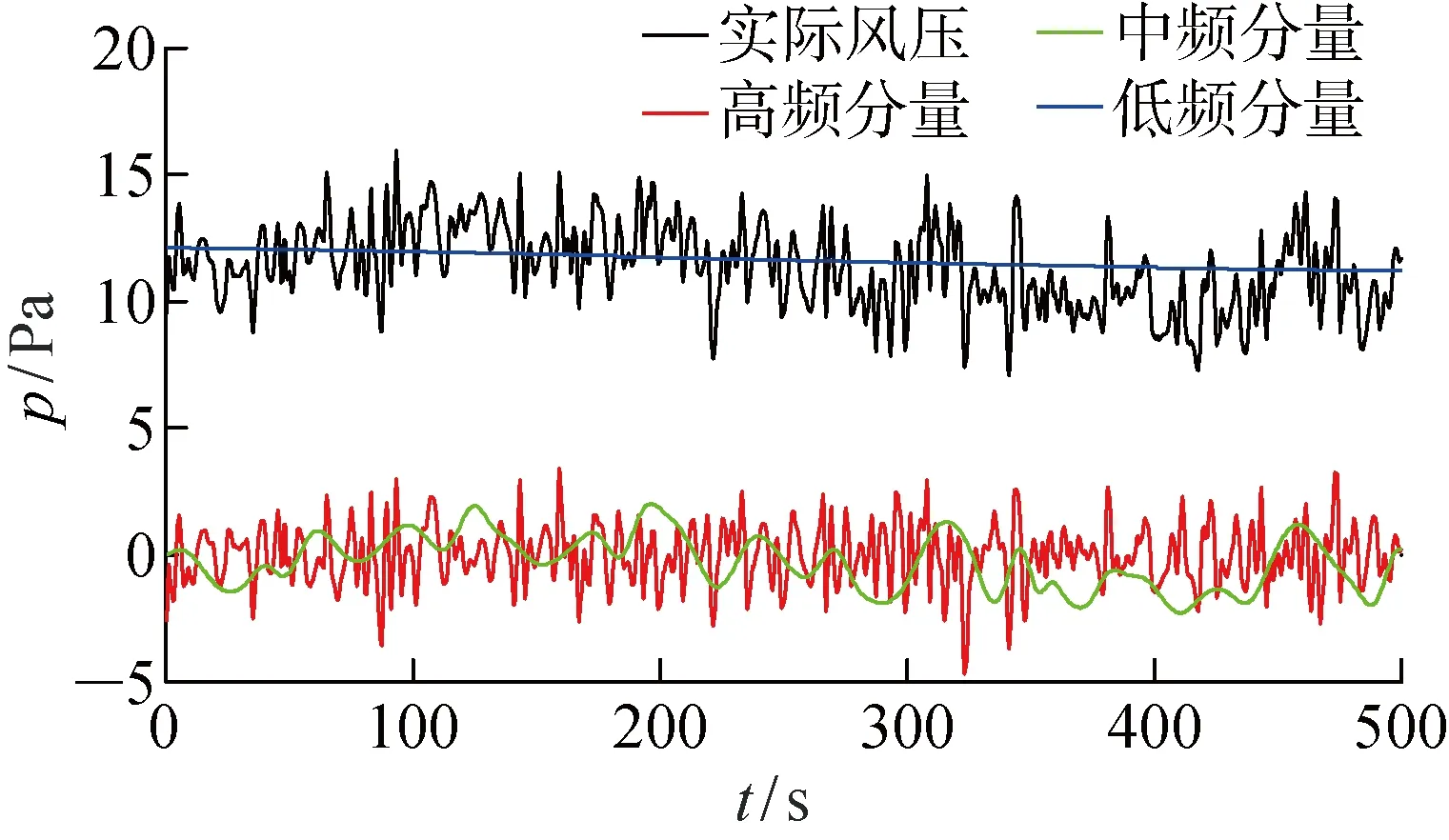
图14 1测点的非平稳风压分量重构图Fig.14 Figure of non-stationary wind pressure reconstruction at Measuring Point 1

表7 3个测点处各分量的游程总数Tab.7 Total number of runs for each intrinsic modal function at the three measuring points

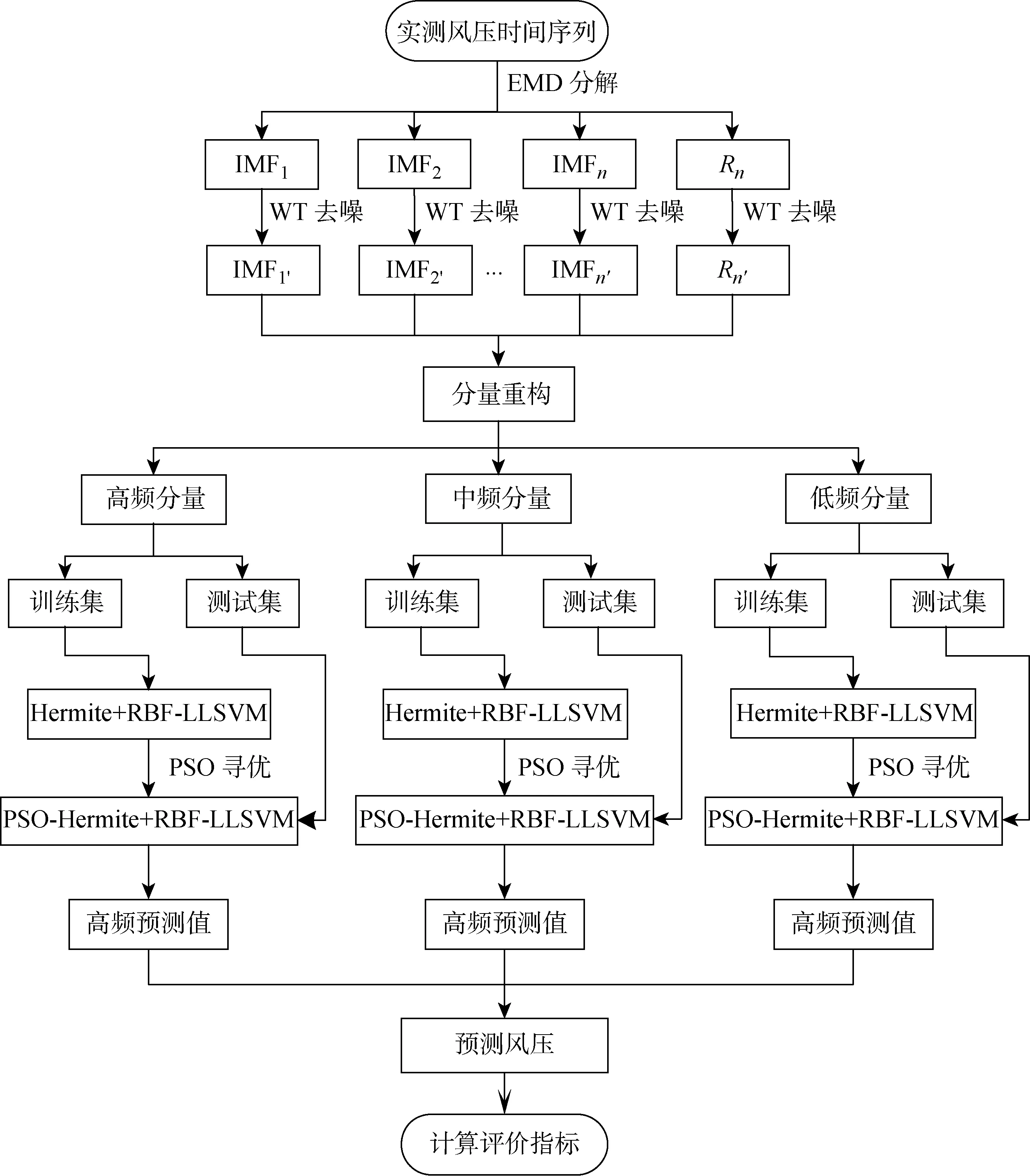
图15 空间点风压预测流程图Fig.15 Flowchart of space point pressure prediction

将3个测点时间长度为500 s的风压实测序列划分为训练集和预测集，取风压实测序列前250 s为训练集，后250 s为预测集，利用训练样本集进行训练学习，构造出确定的输入输出关系，从而建立LSSVM风压预测模型，然后将预测模型应用到预测集，将1，13测点高频、中频以及低频风压数据分别作为输入样本，8测点风压数据作输出，对测点处高、中、低频时间采样序列后250 s风压进行预测，同时给出RBF-LSSVM与Hermite-LSSVM的预测结果作为对比，预测结果如图16所示.

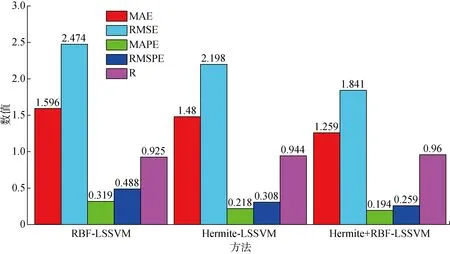
图19 3种预测算法的预测性能评价指标对比Fig.19 Prediction performance indexes of three predicting algorithms

由图16可知，组合核预测模型较其余两种模型效果更好，在空间点预测重构所得的非平稳风压能与8测点处的实际风压更好地吻合.图17为预测风压与实测风压自相关函数和互相关函数对比，图中RBF-LSSVM的结果与实际风压的自相关性存在较大偏差，而组合核预测结果与实际风压的自相关性明显更好.图18为风压及实际风压的功率谱对比，可以看出，混合核模型的预测结果吻合程度明显优于其他两种方法的吻合度.图19中给出了3种模型的5种预测性能指标对比.可以看出，Hermite+RBF-LSSVM模型在空间风压预测中精度最高，MAE、RMSE较RBF-LSSVM分别降低21.1%和25.6%，MAPE和RMSPE分别下降了39.2%和46.9%，较常用的RBF-LSSVM预测性能有较大提升.结合图8和19可知，空间点风压预测效果弱于单点预测，这是由于采用了不同测点处的风压使得样本相关性减弱，预测精度降低.

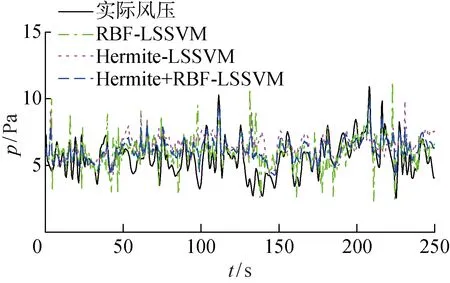
图16 预测风压及实际风压时程图对比Fig.16 Prediction of wind pressure and wind pressure time history diagram

图17 预测风压与实测风压自相关函数和互相关函数对比Fig.17 Comparison of predictive wind pressure and actual wind pressure autocorrelation function and cross-correlation function

图18 预测风压及实际风压功率谱对比Fig.18 Comparison of predicted wind pressure and actual wind pressure power spectrum

4 结论

本文运用3种预测模型对实测非平稳非高斯风压进行了单点及空间点预测.主要结论有：

(1)基于经验模态分解和小波去噪重构的EMD-WT-LSSVM方法对于非平稳非高斯风压预测行之有效，在单点和空间点风压预测中均取得良好的效果；

(2)基于Hermite核函数与RBF核函数的组合核预测模型是一种稳定高精度模型，其在单点和空间点预测结果均优于Hermite-LSSVM及常用的RBF-LSSVM预测模型，处理非线性问题的能力更强，具备较高的工程应用价值.