面向汽车入厂物流系统的订单量协同模型及其算法
张 璇,陈 峰
(上海交通大学 机械与动力工程学院,上海 200240)
汽车零部件入厂物流是汽车物流的重要组成部分,汽车制造商根据生产计划确定每段时间每种零部件的需求量,第三方物流公司根据需求从供应商处取货并配送到制造商仓库,该过程需要制造商、供应商和第三方物流的有效合作,方可避免不必要的费用支出.入厂物流对于减少库存和实现准时制生产都是至关重要的.
目前,有关物流协同模式的研究主要集中在库存路径的问题上.所采用的方法主要有以下几种.
(1)基于分解的启发式算法.该方法一般将原问题分解为多个子问题,如将库存路径问题分解为库存问题和路径问题,再分阶段进行求解.例如:Lei等[1]提出两阶段算法,第一阶段得到直运问题的解,第二阶段对第一阶段的解进行改善;Raa[2]提出基于插入构造和局部搜索的启发式算法;Absi等[3]提出两阶段迭代算法,基于批量大小和分配决策进行迭代.
(2)搜索算法.例如:Moin等[4]提出的分散搜索算法;Belo-Filho等[5]提出的改进的领域搜索法;Vansteenwegen等[6]提出的迭代局部搜索算法.
(3)元启发式算法.例如:陈誉文等[7]提出的基于聚类算法构造初始解的禁忌搜索启发式算法;Mirzaei等[8]提出的基于模拟退火以及禁忌搜索的启发式算法;Azadeh等[9]提出的基于遗传算法的求解方法.
(4)精确算法.例如:Berman等[10]提出基于非线性规划的Lagrange松弛启发式和分支定界法;Archetti等[11]提出分支剪枝算法.
(5)其他方法.例如:Soysal等[12]建立了问题的数学模型并用CPLEX进行求解;Zhong等[13]提出结合DC(Difference of Convex)规划和分支定界法的最速下降混合算法.
以上研究并未考虑订单配送量与需求量的差异可能会对成本产生的影响.因此,本文研究基于订单量的入厂物流协同问题,建立数学模型并提出相应算法,以期降低生产系统的总成本.
1 问题描述与数学模型
1.1 问题描述
本文考虑订单配送量与需求量的差异可能带来的成本增加或减少.对于每个订单,如果配送量小于需求量,会产生缺货带来的风险成本,但可降低其库存成本;如果配送量大于需求量,会产生多余货量的库存成本,但可降低缺货造成的风险成本.此外,考虑到目前物流领域存在货车空载率较高的状况,通过调整订单的配送量,可降低货车的空载率,减少货车的非满载成本.
给定:
承运车的集合{Vk|k=1,2,…,K},其中每辆车的属性包括最大可用容积、固定成本、单位运输成本和单位空载成本;
经销商的集合{Ai|i=1,2,…,S},其中每个经销商可能有1个或多个入厂订单,经销商的属性包括经度和纬度;
入厂订单的集合{On|n=1,2,…,N},其中每个订单属于1个经销商且仅由1辆承运车配送,订单属性包括所属供应商、需求量、单位缺货成本、单位库存成本和最低配送量;
1个入厂物流仓库,所有订单最终配送到该仓库,其属性包括经度和纬度,订单和订单之间、订单和仓库之间的距离通过经纬度计算得到.
总成本包括承运车的固定成本、运输成本、空载成本和订单的缺货成本以及库存成本.承运车的运输成本为承运车单位运输成本与总运输距离的乘积;空载成本为承运车单位空载成本与空载容积的乘积;订单的缺货成本为订单单位缺货成本与订单需求量超过实际配送量的部分的乘积;库存成本为订单单位库存成本与订单实际配送量超过需求量的部分的乘积.
1.2 数学模型
为了降低总成本(C),建立混合整数规划优化模型:
(1)
(2)
(3)
(4)
(5)
x0jk=0
(6)
(7)
(8)
(9)
(10)
Nxijk+ui-uj≤N-1
(11)
式中:
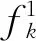



2 优化算法
2.1 启发式算法
本文提出基于贪婪规则的启发式算法.该算法的特点是计算速度快,占用系统资源少且可得到较好的计算结果,可为分支定界算法提供初始上界.步骤如下.
(1)将供应商按订单总量的大小进行降序排列,将每个供应商的订单按订单量多少进行降序排列,得到未装载订单序列(I)并初始化可用承运车序列(D);
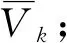
(3)尝试将与Oi′同属1个供应商的其他未装载订单按照需求量装入Vk;
(4)比较以下3个方案:
① 装载Oi′,装载量为Vk的剩余可用容积(vk),则
② 选择Vk已经装载的某个订单Oj,多装载一部分货量,则
③ Vk非满载,则Vk的非满载成本

(5)如果某辆车的装载量比较小,则可以将其换为成本比较低的小型车.对于每辆车的运输路径,选择所有的可行路径中运输成本最小的路径,算法结束.
启发式算法流程如图1所示.

图1 启发式算法流程图Fig.1 Heuristics flow chart
2.2 分支定界算法
分支定界算法是整数规划中一种常用的精确算法,主要包括分支策略、上下界设计以及搜索模式与支配规则3部分,其基本思想是基于分支策略,将原问题分解成规模较小的子问题.
2.2.1分支策略 分支策略是将问题分割成子问题的方法,即如何确定分支节点,每个节点对应1个子问题和相应的子空间.本文将承运车配送订单视为1个装箱问题,每个订单的每种可能的配送量作为1个节点.
解的搜索从第1层开始,第1个订单选择1种可能配送量和可能装入的车,如果该订单有Q1种可能的配送量,则第1层可能会有Q1K个节点;如果第2个订单有Q2种可能的配送量,对应Q2K种选择方案,则第2层可能有Q1Q2K2个节点,依此类推.如果Q1=Q2=…=QN=Q,则N个订单最终最多会产生QNKN个节点.实际中,部分节点不可行或者节点的下界大于全局上界(Bu),则该部分节点会被剪枝,所以实际节点数Nr 2.2.2上下界设计 合理的上下界设计可以有效剪枝,缩小搜索空间,从而提高搜索效率.本文模型的优化目标为总成本最小,当1个节点的局部下界大于Bu时,该分支将被剪除.以启发式算法的解作为初始上界进行搜索,当寻找到比当前上界更小的解时,更新Bu. 对于1个节点的下界,首先计算该节点全部尚未装载订单的最低配送量qL和所有承运车的剩余可用容积vR.如果qL≤vR,则节点的下界为当前已装载订单的缺货成本和库存成本,以及已经装载了订单的承运车的固定成本和最小运输成本.如果节点的下界不小于Bu,则该节点被剪除. 2.2.3搜索模式与支配规则 分支定界的搜索模式包括深度优先模式以及广度优先模式.深度优先模式优先搜索深层节点直到叶节点或者剪枝;广度优先模式则同时计算同一层的多个节点,将会占用更多的系统内存.因此,本文选择深度优先模式进行搜索. 支配规则为优先选择排序较为靠前的订单进行分支. 2.2.4算法流程 (1)以启发式算法的解为初始上界,初始化I. (2)如果存在未装载订单,选择I中的第1个订单Oi,并将Oi从I中删除;否则转步骤(5). (3)如果已遍历Oi的所有可能配送量和选车方案,转步骤(2);否则选择一个方案作为一个分支节点. (4)如果选择的配送量不超过所选车的剩余可用容积且节点下界(Bl)小于Bu,转步骤(2);否则转步骤(3). (5)以所有可能配送路径中运输成本最低的路径作为该节点的路径,计算该节点的总成本,如果C (6)Bu为最优解,算法结束. 分支定界算法流程如图2所示. 图2 分支定界算法流程图Fig.2 Branch and Bound algorithm flow chart 用C#语言在Visual Studio平台开发测试程序,调用ILOG CPLEX求解混合整数规划模型进行数值实验. 表1 承运车信息Tab.1 Information of carrier vehicle 表2 实验设计Tab.2 Design of experiments 表3 模型与算法总成本对比Tab.3 Comparation of model and algorithms total cost 为分析订单量协同对总成本的影响,将式(9)替换为 (12) 上式表示每个订单的配送量等于需求量,即得到非订单量协同问题的数学模型. 利用表2中的数据以及CPLEX模型求解非订单量协同问题的数学模型,求解时间上限为30 min.将计算结果与订单量协同问题的总成本进行比较,结果如表4所示.可以看出,订单量协同可以有效降低系统的总成本. 表4 订单量协同与非订单量协同的总成本对比Tab.4 Comparation of collaborative and non-collaborative total cost 为了分析订单总需求量对固定成本、运输成本、库存成本、缺货成本、空载成本和总成本的影响,指定可用承运车的集合为{C60,C40,C40},选择同一个供应商的15个订单,适当调整订单总需求量,分析总成本的变化趋势.对于每组数据,分别用CPLEX数学模型以及分支定界算法进行求解,时间上限为30 min,选择两者中总成本较低者进行对比,结果如表5所示. 表5 订单总需求量对成本的影响Tab.5 Impact of total order quantity on costs 可以看出,当订单总需求量较小时,只使用2辆承运车运输所有订单.此时,有些订单配送量小于其需求量,即产生缺货成本,但缺货成本小于多使用1辆承运车对应的固定成本、运输成本和空载成本.随着订单总需求量的增加,缺货成本的增加量超过了多使用1辆承运车对应的固定成本、运输成本和空载成本,故使用3辆承运车.此时,固定成本和运输成本增加,缺货成本为0并产生库存成本和空载成本.可见,订单的总需求量对总成本的影响主要体现为权衡不同的成本因素,以使总成本最低. 本文研究了基于订单量的入厂物流协同,建立了混合整数规划模型,提出了启发式算法和分支定界法.通过数值实验验证了模型和算法的有效性.结果表明,订单量协同可以有效降低系统的总成本;订单的总需求量对总成本的影响主要体现为权衡不同成本因素以使总成本最低.
3 数值实验与结果分析
3.1 算法对比



3.2 订单量协同效应

3.3 订单总需求量对成本因素的影响

4 结语

