异形盾构管片原型试验混凝土裂缝宽度预测与可视化

朱叶艇，朱雁飞，张子新，庄欠伟，郑宜枫

(1.上海隧道工程有限公司,上海 200233；2.同济大学 地下建筑与工程系,上海 200092)

国内外很多大型盾构隧道或者新型盾构隧道结构型式在建造前都会进行原型加载试验以评价结构设计的合理性和可靠性，同时研究在不同荷载状态下管片结构的力学响应和极限破坏特征.代表性地，Nakamura等[1]分别对不带立柱和带立柱的三环错缝拼装类矩形盾构隧道衬砌结构进行足尺加载试验，研究类矩形盾构管片在浅覆土和深覆土条件下的结构力学行为规律.何川等[2]创新地研发了采用钢绞线环箍管片模拟水压荷载的多功能盾构隧道结构加载试验系统，分别对不同拼装条件下南京长江隧道和狮子洋水下盾构隧道衬砌结构的力学行为和破坏特征进行研究.Liu等[3]采用24点加载方案对上海地铁圆形盾构管片进行原型极限加载试验，重点对衬砌结构形变演化、接头张开和裂缝开展进行研究.Afshan等[4]通过铸铁管片结构试验研究新建隧道施工对邻近盾构隧道管片引起的大变形条件下的衬砌结构力学响应.

异形盾构隧道因断面型式类圆形且类矩形，相较于圆形隧道和矩形隧道分别具有高空间利用率和高结构承载能力的特征，可以预见其未来在城市地铁、下立交、公路隧道等工程中广阔的应用前景.以往的盾构管片原型加载试验都基于“平躺式”的试验方法进行，弱化甚至忽略管片结构自重对其内力和形变的影响.异形盾构衬砌结构力学特征较矩形和圆形盾构隧道更为复杂，前期的数值计算[5]和后期的原型试验结果[6]共同证明浅覆土条件下自重对异形盾构衬砌结构内力和形变影响巨大，因而进行“站立式”原型管片结构加载试验，考虑自重对衬砌结构力学行为规律的影响.

管片混凝土极限开裂特征是原型管片加载试验研究的重中之重.正常使用状态下管片结构破坏标准为：① 管片最大裂缝宽度不超过 0.2 mm[7]；② 管片混凝土应力达到或超过其抗压强度；③ 接头螺栓应力达到屈服强度.数值模拟和原型管片结构试验[6]均证明异形盾构管片拱顶为受力最不利截面，其内弧面裂缝宽度超过 0.2 mm会先于第二和第三条破坏标准发生.因此，预测和可视化实测管片混凝土裂缝宽度和开展规律对整个原型管片试验加载系统的研发以及后续的管片优化设计至关重要.

需要说明的是，异形盾构管片裂缝宽度的预测基于《纤维混凝土结构技术规程》[8]第 6.1.6 条钢纤维混凝土最大裂缝宽度理论公式进行，须提前获得管片截面弯矩和轴力.再者，由于异形盾构设计暂无相关设计规范和借鉴案例，为提高管片混凝土的抗裂性能，在满足实际混凝土和易性的前提下，本文管片混凝土采用体积率为 2.0% 的CF50钢锭铣削型钢纤维混凝土，但该体积率已经超出《纤维混凝土结构技术规程》范围，裂缝宽度理论计算公式中相关计算参数须通过梁荷载试验获取.另外，原型加载试验过程中管片处于拼装受荷状态，人为进行裂缝搜索和勾勒测量是不被允许的.因此，寻找一种能对特定区域进行持续性非接触式的图像采集监测技术成为原型管片结构试验的重要任务.自从1983年Sutton等[9]第一次提出数字图像相关方法(Digital Image Correlation,DIC)，基于双目立体视觉原理的DIC-3D技术已经广泛应用于实验力学领域[10-12].DIC可通过跟踪变形前图像中以各选定计算点为中心的图像小区在变形后图像中的位置变化来获得各计算点的位移信息[13]，从而获取非平面状态下全域位移分布和应变分布，并基于一定的处理方法判定裂缝出现时机和获取裂缝宽度值.

本文从裂缝宽度预测和可视化实测入手，一方面通过梁构件荷载试验完善体积率为2%的CF50钢纤维混凝土梁裂缝宽度理论计算公式，为异形盾构管片裂缝宽度预测提供理论方法；另一方面基于DIC-3D技术，在拱顶内弧面设置测试区域，通过图像数据处理技术揭示裂缝出现时机和计算裂缝宽度值，为掌握裂缝发生发展规律以及为未来DIC-3D技术应用于大型结构试验提供借鉴经验.

1 试验概况

1.1 钢纤维钢筋混凝土梁荷载试验

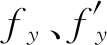
图1 正截面受弯承载力计算简图Fig.1 Calculating diagram of normal section bending bearing capacity

根据文献[8]第5.2.1条有：

x=βxn

(1)

(2)

式中：xn为截面实际受压区高度，由试验实测获得.

式中：ft、fc为混凝土轴心抗拉强度设计值和轴心抗压强度设计值；βtu为钢纤维对受拉区钢纤维混凝土抗拉作用的影响系数，由试验确定；λf为钢纤维含量特征值，本文取值 0.686；α1为受压区混凝土等效应力值的影响系数，根据文献[8]规定，取值 1.0.

因此，结合图1并根据力的平衡原则，受弯构件正截面受弯承载力Mfu可表示为

(5)

综上，β和βtu为梁截面内力求解所需参数，可通过梁多级荷载试验确定.最终，偏心受压构件梁截面弯矩M和轴力N为

(6)

式中：σc、σt分别为梁截面受压区和受拉区边缘混凝土压应力和拉应力，可表示为

(7)

式中：εc、εt分别为梁截面受压区和受拉区边缘混凝土压应变和拉应变，由试验实测获得；Ec为混凝土弹性模量.

根据文献[8]第 6.1.6 条规定：矩形截面钢筋钢纤维混凝土受弯构件、大偏心受压构件、受拉构件最大裂缝宽度wfmax可表示为

wfmax=wmax(1-βcwλf)

(8)

(9)

式中：wmax为根据钢纤维混凝土的强度等级，不考虑钢纤维的影响的钢筋混凝土构件最大裂缝宽度；βcw为钢纤维对钢纤维钢筋混凝土构件裂缝宽度的影响系数，通过试验确定；αcr为构件受力特征系数；ψ为裂缝间纵向受拉钢筋应变不均与系数；Es为钢筋弹性模量；cs为最外层受拉钢筋外边缘至受拉区底边的距离；ρte为纵向受拉钢筋配筋率；deq为受拉区纵向钢筋等效直径.

σs为纵向受拉钢筋等效应力，须利用式(6)中M和N计算而得，故计算梁构件最大裂缝宽度需要首先计算截面内力.

1.1.2试验方法 为尽可能地获得适用于异形盾构管片截面内力和最大裂缝宽度理论公式所需的计算参数，本次钢纤维钢筋混凝土梁荷载试验构件为300 mm×300 mm×550 mm的非标准件(见图2).上、下两排分别为2根和3根直径为12 mm的HRB400钢筋，构件配筋率与管片配筋率一致.

如图3(a)所示，在梁中间截面对应位置的纵筋和混凝土梁外表面设置BX120-3AA箔式应变计，并在梁顶面设置3个BX120-50AA箔式应变计(见图3(b))，以获取纵筋应变和混凝土表面应变.采用康科瑞KON-FK(B)裂缝宽度测试仪(量程10 mm)量测混凝土裂缝宽度.

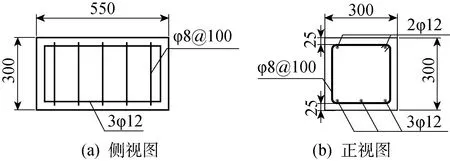
图2 梁配筋图(mm)Fig.2 Reinforcement layout of the beam (mm)

图3 测点布置示意图(mm)Fig.3 Layout of measuring points (mm)

试验加载和控制设备如图4所示.将梁构件放置于铰支座之上，通过分配梁将千斤顶荷载平分成两个线荷载施加于梁顶面.

图4 梁加载图Fig.4 Loading diagram of the beam

1.2 原型管片试验裂缝可视化监测

1.2.1原型管片力学试验概况 异形盾构管片设计如图5所示，管片外径 10.7 m×8.2 m，通过块之间4根M30直螺栓和环之间26根M33弯螺栓完成错缝拼装[14].

图5 异形盾构管片设计图(mm)Fig.5 Design plan of special-shaped segment (mm)

图6 试验平台Fig.6 Testing platform

如图6所示，本次站立式管片原型试验将三环管片错缝拼装于钢加载反力架内，通过88个环向对称分布的千斤顶施加地层荷载，并利用30组纵向加紧装置模拟纵向顶推力.

1.2.2裂缝可视化监测方案 如表1所示，整个加载过程共分为36步，每一步对应相应的管片覆土深度db和静止侧压力系数λ.其中，前22步模拟设计地层施工工况，第23步至33步模拟设计地层运营工况，最后3步模拟设计地层卸载工况.

表1 加载步与覆土深度对应关系Tab.1 Correspondence between the step numbers and buried depths

管片拱顶内弧面三个测试区域如图7所示，将3套DIC-3D专业定制版系统(每个观测区域尺寸 0.8 m×0.8 m，CCD像元尺寸3.45 μm，分辨率 2 448 像素×2 048 像素，12 mm镜头)相机部分固定于距离待观测区域1.5 m处.人工将哑光白自喷漆均匀喷射在待观测区域，并用黑色油性笔轻戳出大量直径约为2 mm的散斑，使待测区域表面整体上形成随机的灰度分布.调节相机俯仰角及相机间夹角，直至左右相机视图中均显示同一片待观测区域且充满视场后锁紧相机.拧松镜头光圈控制螺丝，调节光圈至全场清晰成像.调节光源，待光场均匀后锁紧光源，并调节光源前端和镜头前端的偏振片，消除杂散光.采用9行12列共108个圆点，圆心距为25 mm的圆点标定板完成系统标定后开始图像采集，采集帧率为10帧/s.

作为一种规律，对于普通猪禽饲料而言，调质过程中，物料温度每升高10℃，水分增加0.6%～0.7%[9]。但对于水产饲料而言，因饲料吸水率较低，采用高压、低蒸汽量、长时间调质，温度每升高10℃，水分增加0.5%～0.6%。对反刍动物的精料补充料也有类似的情况。

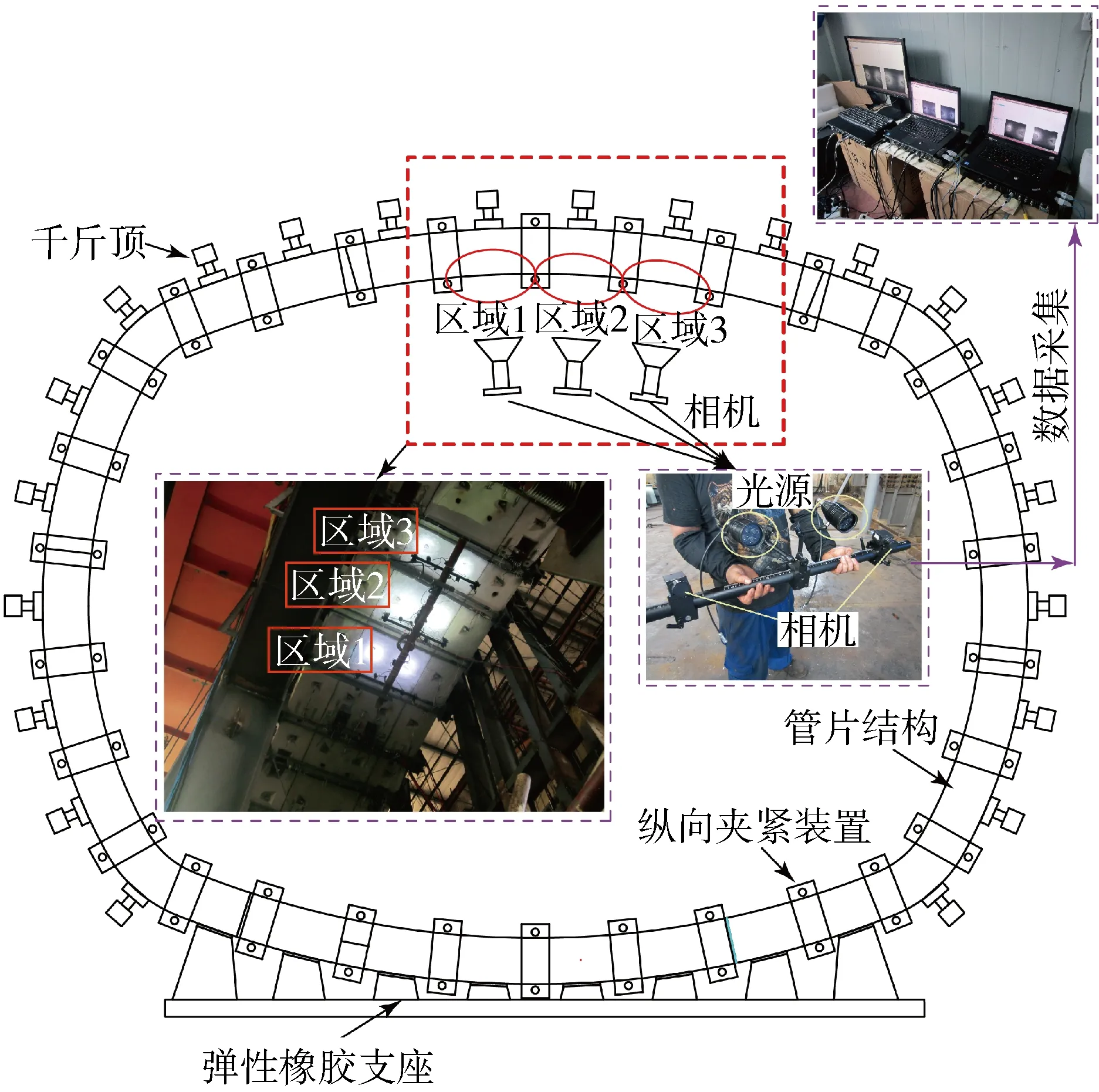
图7 测试区域和测试设备Fig.7 Monitoring zones and equipment

1.2.3DIC-3D基本原理 如图8所示，双目立体视觉[13]的基本原理与人类的视觉原理类似，即须通过两个摄像机从不同方位分别同时记录同一空间场景中的待测P点，使其分别成像于左、右摄像机像平面上的P1点和P2点.Oc1和Oc2分别表示左、右两个摄像机的光心，P点即为Oc1P1和Oc2P2两条直线的交点.通过预先人为设定的世界坐标系，根据由标定得到的两个摄像机的内外部参数，就可以计算得到该点在空间中对应坐标系的三维坐标，变形前后待测点P的空间坐标之差即为待测点P的三维位移.对三维位移场进行差分计算或平滑后再差分计算即可求得相应的应变场.

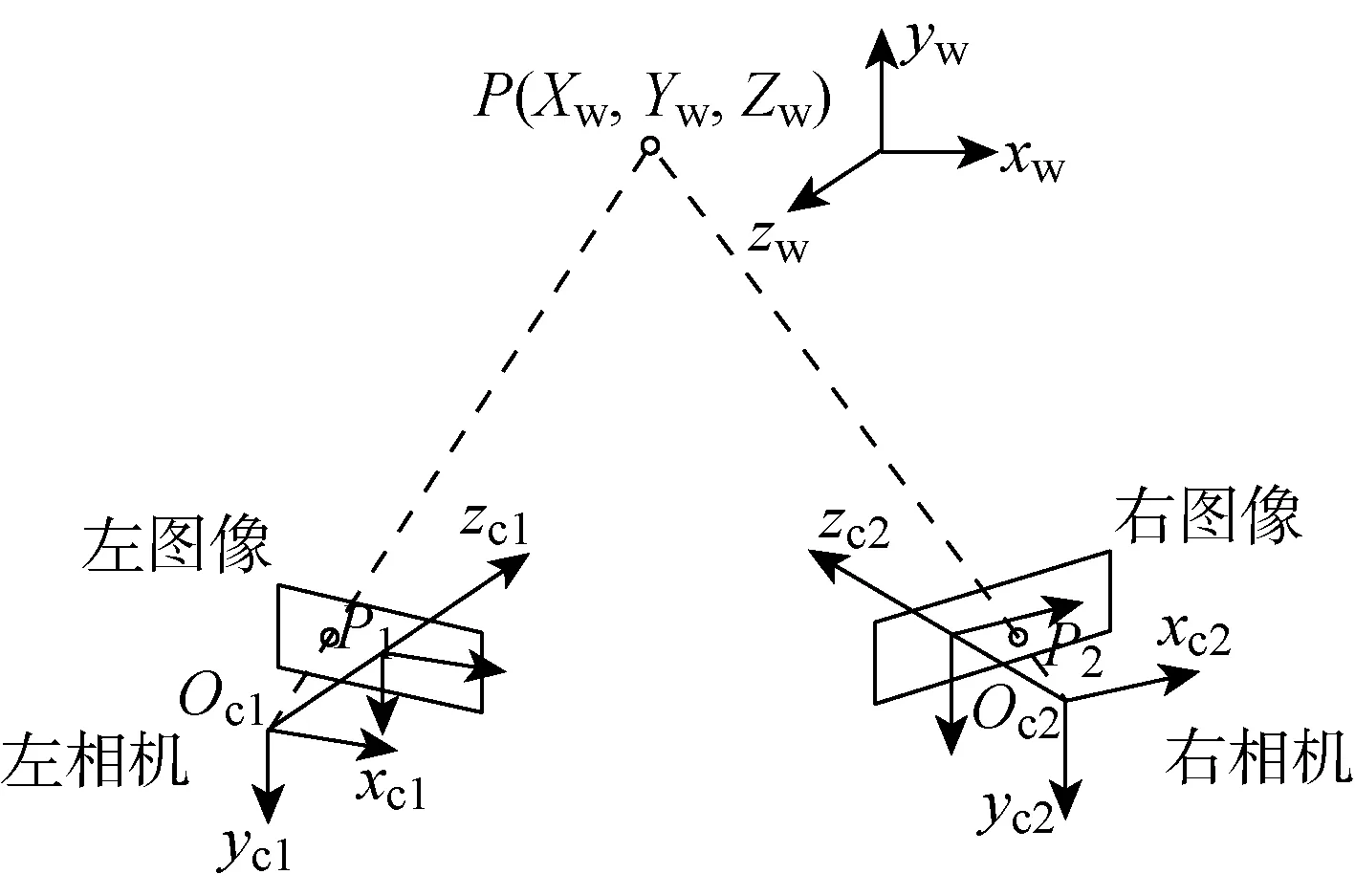
图8 双目视觉原理图Fig.8 The principle of binocular stereovision

2 试验结果分析

2.1 管片原型试验裂缝可视化分析

2.1.1相关计算 根据极限破坏工况加载进程和试验数据采集时间表，对照DIC-3D系统图像采集时间记录及10 帧/s的采集速度，依次找出区域1、2、3对应于各极限破坏工况数据稳定时间的图片帧序号，再将它们提取出来按顺序从加载步0至加载步36编号，作为DIC-3D待分析图像.在DIC-3D分析系统中导入筛选后的散斑图像进行相关计算和分析.裂纹出现时，裂纹两侧垂直裂纹方向的位移场和最大主应变场变化情况会明显不同，并在裂纹两侧呈现出明显的梯度变化.

图9 计算区域1和种子点Fig.9 Calculation region and the seed in Zone 1

以区域1为例(见图9)，相关计算是指在参考图中(加载步0)选取感兴趣的计算区域(AOI)，根据选定的网格点间距(本文为5像素)划分网格，以网格点为中心选取图像子区作为模板(即子区大小，以网格点为中心选取的图像子区的大小，较小的模板尺寸拥有较高的空间分辨率，但同时过小的模板子区细节不够丰富，难以精确匹配，本文定为49像素)，然后用归一化的最小平方距离相关函数(ZNSSD)相关准则[12]匹配网格点在变形图中的位置.参数设置好后，进行种子点分析，即在参考图右相机图像及后续的36对图像序列中匹配出种子点位置.种子点分析完成后继续计算，得出整个相关计算区域内各点的匹配关系.

2.1.2重构分析 如图10所示，三维重构及应变计算后，建立以试件中部为原点，水平向右为x轴正向、竖直向上为y轴正向，离面朝外为z轴正向的全局坐标系.

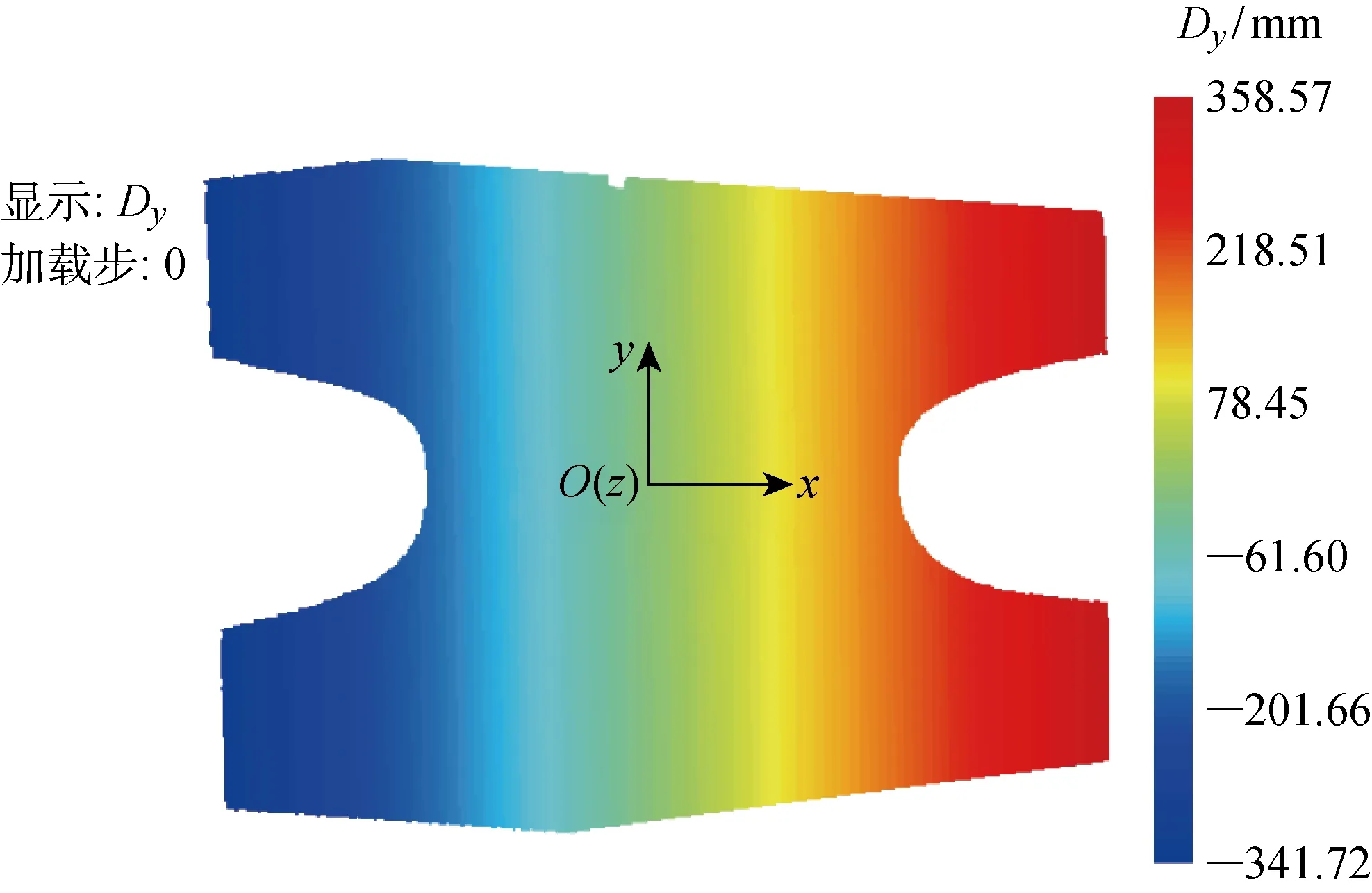
图10 全局坐标系Fig.10 Global coordinate system

位移场、应变场都是当前帧相对于参考图计算获得的.其中，图11(a)为所建立的坐标系下加载步36相对于加载步0的y向位移场Dy，从颜色分布可以直观地看出Dy场在区域1上、中、下部各形成1条颜色突变线，且线的走向为横向，线的上下部Dy值有明显的突变；图11(b)为加载步36相对于加载步0的最大主应变场E1，同样也可以看出上、中、下部各有1条应变数值明显较大的“线”，全场其余位置应变值都较小.通过与图11(c)裂缝实际勾勒图对比确认，区域1共有3条明显的裂缝，从上至下裂缝分别命名为1-A、1-B和1-C.

(1)裂缝出现时机判定方法.在DIC-3D软件分析界面中，观察加载步0至加载步36的二维贴图，找出加载步36中主裂缝1-A明显较宽的一些位置，并垂直于裂纹走向绘制阶段线(即SL，该线段从起点至终点等距分布一系列网格点)，依次记为 SL1-0～SL1-4(见图11(a))，并绘制这些阶段线的Dy空序曲线(阶段线中各网格点位移分布曲线).其中，横轴代表距阶段线起点的距离，纵轴代表Dy值.观察加载步0至加载步36各个加载步5条阶段线的空序曲线变化情况，发现阶段线SL1-1的Dy空序曲线率先在加载步4(db=5 m，见图12(b))时出现了稳定-跌落-稳定的分布，而加载步3(db=4 m，见图12(a))时未出现此规律分布，可以得出加载步4为裂缝1-A出现裂缝的时机.

根据此方法同样可以判断出：裂缝1-B在加载步3(db=4 m)出现在阶段线SL1-9处，裂缝1-C在加载步5(db=6 m)出现在阶段线SL1-12处.

图11 E1和Dy场以及裂缝实际勾勒图Fig.11 E1 and Dy fields and actual sketching map of cracks

图12 阶段线SL1-1的空序曲线Fig.12 Change of the spatial sequence curves for SL1-1

(2)裂缝宽度w计算方法.考虑到裂缝的影响，理论上应在垂直裂缝走向并靠近裂缝两侧选取两网格点，这两点垂直于裂缝走向的位移差即为裂缝宽度.但是相关计算区域绘制时会包含裂缝，而裂缝处位移计算有一定的平滑效应，且子区大小为49像素，因此在裂缝两侧25像素外位置处各绘制一小矩形区域(即SR，该区域包含一定数量的网格点)，再建立以每条阶段线与裂缝交汇处为原点，以垂直该裂缝走向为y轴的局部坐标系，最终将局部坐标系下两矩形区域内的Dy均值之差作为裂纹宽度.

因此，可得如图13所示的区域1内3条裂缝共14条阶段线在各自局部坐标系下对应的上、下阶段矩形Dy均值差(裂缝宽度)随加载步的变化曲线.

纵观区域1内3条裂缝各阶段线对应裂缝宽度随荷载增加基本呈“三阶段”规律：

阶段一，初始阶段.初始阶段，结构承受外荷载较小，裂缝尚未出现，衬砌混凝土处于小变形阶段.

阶段二，稳定阶段.管片结构整体处于弹性状态或者局部弹塑性阶段，结构形变和管片混凝土应变在此阶段随荷载增加呈线性增长趋势.

阶段三，加速阶段.管片整体结构处于塑性阶段，混凝土开裂加快，裂缝宽度随荷载增加呈指数增长趋势.

究其原因，如图14和15所示，异形管片结构整体呈竖向闭合、横向张开的“横鸭蛋”形.将结构在竖向对称轴方向的形变定义为竖向闭合量Dver，在水平对称轴方向的形变定义为横向张开量Dhor，并将竖向和水平向横向刚度有效率分别定义为η1和η2.基于试验仪器安全考虑，加载至db=16 m后管片形变量测设备被撤出，后续管片形变未能捕捉.从图14和图15中可以看出，管片形变和横向刚度有效率随db增加呈两阶段分线性增长趋势：当隧道db小于14 m，管片结构形变和横向刚度随db增加呈线性增长趋势，说明管片结构整体处于线弹性状态；当隧道db超过14 m后，管片结构形变增长速率稍有变大，横向刚度有效率略有下降，说明管片结构进入局部弹塑性阶段直至整体塑性阶段.

图13 区域1各阶段线处裂缝宽度随加载步变化规律Fig.13 Variation of the crack widths for each step line with the loading steps in Zone 1

图14 管片形变量随覆土深度变化规律Fig.14 Variation of the segmental deformations with buried depths

图15 管片横向刚度有效率随覆土深度变化规律Fig.15 Variation of transverse effective rigidity ratios with buried depths

至加载结束，裂缝1-A宽度并未达到0.2 mm，裂缝宽度最大值位于阶段线SL1-1处，约为0.19 mm；至加载结束，裂缝1-B中阶段线SL1-5、7、8、9处裂缝宽度均超过了0.2 mm，阶段线SL1-7、8处裂缝宽度增量最大，在加载步32(db=23 m)时均已达到0.2 mm；至加载结束，裂缝1-C中阶段线 SL1-10～SL1-13处裂缝宽度均超过了0.2 mm，阶段线SL1-13在加载步32(db=23 m)时裂缝宽度达到0.2 mm，裂缝宽度最大值(0.28 mm)同样位于阶段线SL1-13.

图16 区域2和3阶段线和阶段矩形绘制Fig.16 Sketching of the step lines and step rectangles in the displacement contours of Zone 2 and 3

图17 区域2和3各阶段线处裂缝宽度随加载步变化规律Fig.17 Variation of the crack widths for each step line with the loading steps in Zone 2 and 3

将区域2和3的位移场云图以及阶段线和阶段矩形的绘制示于图16，并将各阶段线在对应局部坐标系下的裂缝宽度随加载步变化规律示于图17.需要说明的是，在极限破坏工况之前，测试区域2中3条裂缝(2-A、2-B和2-C，见图16(a))和测试区域3中的2条裂缝(3-A和3-B，见图16(b))已经存在，但宽度极小，并未达到破坏标准.至加载结束，该区域也未出现新的裂缝，而已有的裂缝宽度明显增加.因此，本文针对已有的裂缝进行监测，采用裂缝宽度的增量作为本测试区域裂缝宽度值.

如图17(a)所示，除区域2中裂缝2-B(黑圈范围内的3条阶段线)未经历裂缝开展加速阶段以外，其余的裂缝与区域1中的裂缝相似，都经历了裂缝开展三阶段.

如图17(a)所示，加载步32(db=23 m)时，裂缝2-A中阶段线SL2-1所在位置裂纹宽度超过0.2 mm，至加载结束宽度达到0.31 mm；至试验结束，裂缝2-B裂缝宽度均未达到0.2 mm，最大值(0.13 mm)位于阶段线SL2-6处；至加载步24(db=18.5 m)时，裂缝2-C中阶段线SL2-9、10所在位置处裂缝宽度均达到0.2 mm，至加载结束，阶段线SL2-9、10处裂缝宽度也均达到最大值(0.39 mm).

如图17(b)所示，加载步33(db=24 m)时，裂缝3-A中阶段线SL3-1所在位置的裂缝宽度达到了0.2 mm，至加载结束时为0.26 mm；加载步24(db=18.5 m)时，裂缝3-B中阶段线SL3-3所在位置的裂缝宽度达到0.2 mm，至加载结束，裂缝宽度达到最大值0.40 mm.

综上，测试区域2中裂缝2-C和测试区域3中裂缝3-B在db=18.5 m时，裂缝宽度同时达到0.2 mm，即达到设计要求的管片结构破坏标准.因此，本文将18.5 m作为异形盾构衬砌结构的极限覆土深度.

2.2 最大裂缝理论宽度预测方法

钢纤维混凝土梁荷载试验[6]获得混凝土受压区等效矩形应力图形高度系数β为0.56，正截面受拉区钢纤维混凝土抗拉作用的影响系数βtu为0.75，钢纤维对钢筋钢纤维混凝土构件裂缝宽度的影响系数βcw为0.91.最终，式(6)和(8)得以完善，异形盾构管片截面弯矩M和轴力N为

(10)

最大裂缝宽度为

wfmax=0.38wmax

(11)

为验证截面设计参数有效性，本文基于隧道覆土17 m时的原型试验监测数据，通过式(10)计算获得管片内力分布如图18所示.图中：弯矩分正负；拉力为正，压力为负.从图18可以看出，异形盾构管片最大正弯矩(+1 047 kN·m)位于拱顶，对应轴力 1 653 kN，通过式(11)计算最大裂缝宽度理论值为0.209 mm，管片结构达到理论破坏标准.该覆土深度与上述DIC-3D技术实测极限覆土深度接近，证明了理论公式计算参数的有效性.

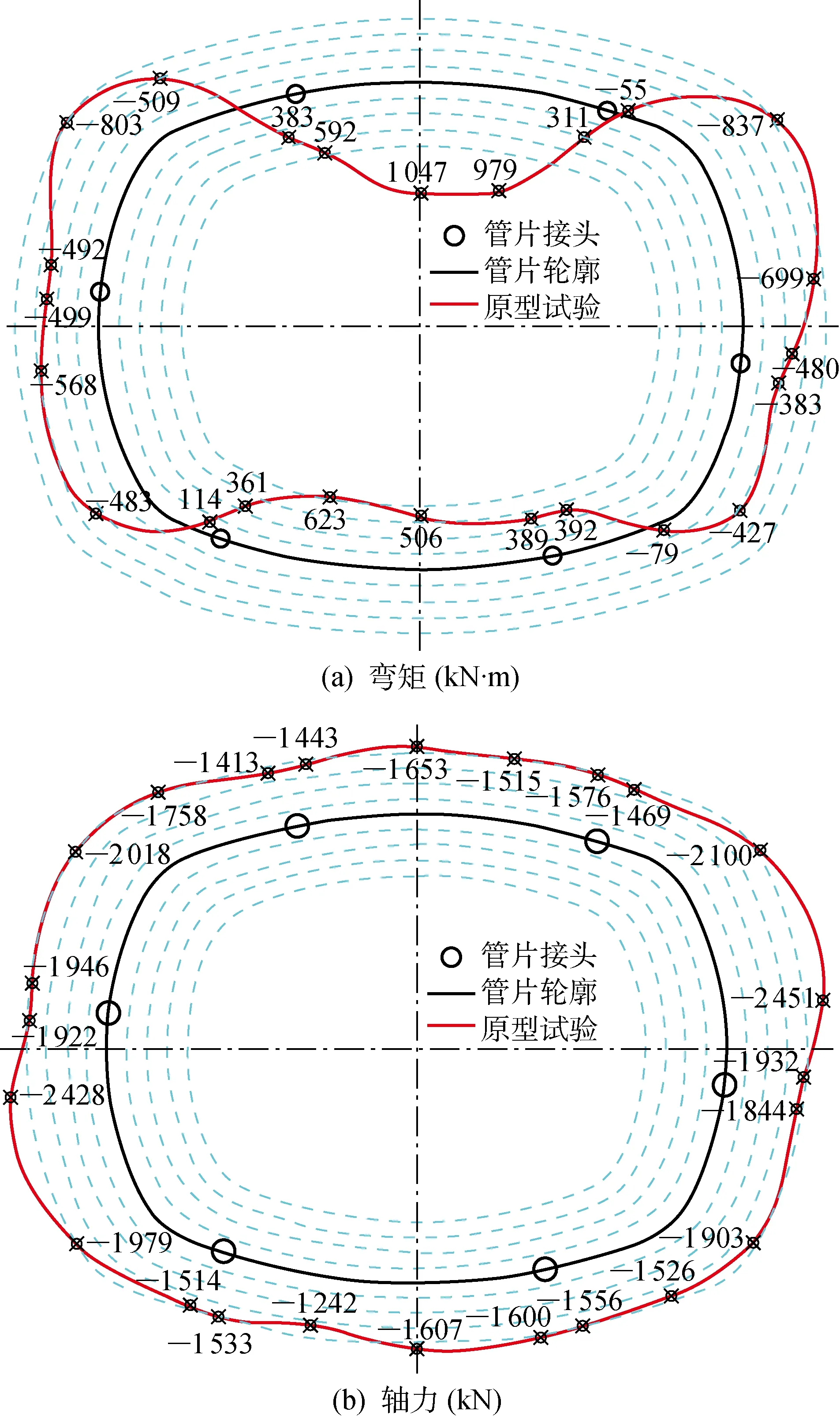
图18 17 m覆土深度下管片内力分布Fig.18 Distribution of the internal forces in the buried depth of 17 m

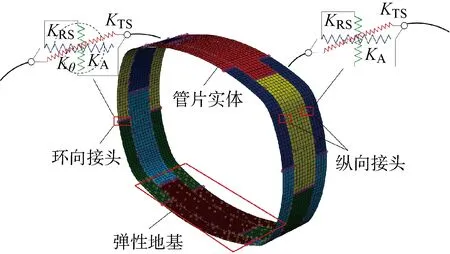
图19 异形盾构管片壳-弹簧模型Fig.19 Shell-spring model for special-shaped tunnel

未来对于异形盾构管片混凝土裂缝宽度的预测须先获得管片结构的内力.已有的研究成果[15-16]一致认为，壳-弹簧模型可以较为真实地反应管片内力真三维分布.图19所示为异形盾构管片壳-弹簧模型，图中：Kθ为接头转动刚度；KA为接头轴向抗压刚度；KTS为接头轴向剪切刚度；KRS为接头径向剪切刚度.

本文作者将异形盾构管片结构试验结果与壳-弹簧模型计算结果进行对比，同样验证了该模型的有效性[6].故提出未来可先通过壳-弹簧模型进行异形盾构管片内力计算，并结合梁荷载试验所获计算参数进行混凝土裂缝宽度的科学预测.

3 结论

本文通过钢纤维混凝土梁荷载试验和原型管片裂缝DIC-3D可视化监测试验，对异形管片混凝土裂缝宽度进行研究，得出以下结论：

(1)通过原型异形盾构管片加载DIC-3D裂缝监测试验，给出了裂缝出现时机判定方法和裂缝宽度计算方法，对管片混凝土裂缝开展特征进行了研究，提出了反映管片整体结构受力特性的裂缝开展三阶段规律，并确定出异形盾构管片极限覆土深度为18.5 m.

(2)通过钢纤维混凝土梁荷载试验完善了CF50钢纤维混凝土裂缝宽度理论计算公式，并基于理论公式预测的异形盾构管片极限覆土深度与DIC-3D技术实测的极限覆土深度接近，证明了理论公式的合理性和裂缝可视化监测的科学性.

(3)未来可基于壳-弹簧模型获取异形盾构管片最不利断面的内力，并通过理论公式预测管片极限覆土深度，这将为未来异形盾构的设计优化提供有力的理论支持.