基于动网格技术的双定子马达配流结构优化

刘巧燕 闻德生 吕世君

(1.黄淮学院智能制造学院， 驻马店 463000； 2.燕山大学机械工程学院， 秦皇岛 066004)

0 引言

由闭死现象造成的高压回流冲击是叶片马达产生振动和噪声的主要原因之一，对马达的正常工作影响较大[1-6]。从20世纪70年代开始，国内外已开始重视对降低泵和马达噪声的研究，因此出现了很多性能优良的低噪声泵和马达[7]。

双定子叶片马达是基于国际专利技术的一种新型液压元件[8-9]，形成了一个壳体内存在一个转子对应两个定子的结构，可以组成多个相互独立的单马达，各单马达可以分别单独工作、联合工作以及差动工作。目前已对双定子系列元件进行了较多分析与研究[10-21]，但是，双定子马达也同样存在着因闭死容腔内压力急剧变化而引起的定子、转子径向振动问题。

动网格模型可以用来模拟由于流体域边界运动或边界变形引起的流体域形状随时间变化的各种流动问题。由于马达一直处于运动状态，而静态分析不足以说明问题。因此本文采用动网格技术对双定子马达的配流以及闭死容腔内压力的变化特性进行研究。

1 双定子马达配流

双作用双定子马达通常取定子曲线的大、小圆弧区段的幅角与相邻两叶片之间间隔角相等，图1为双作用双定子马达的原理简图，图2为马达三维结构图。

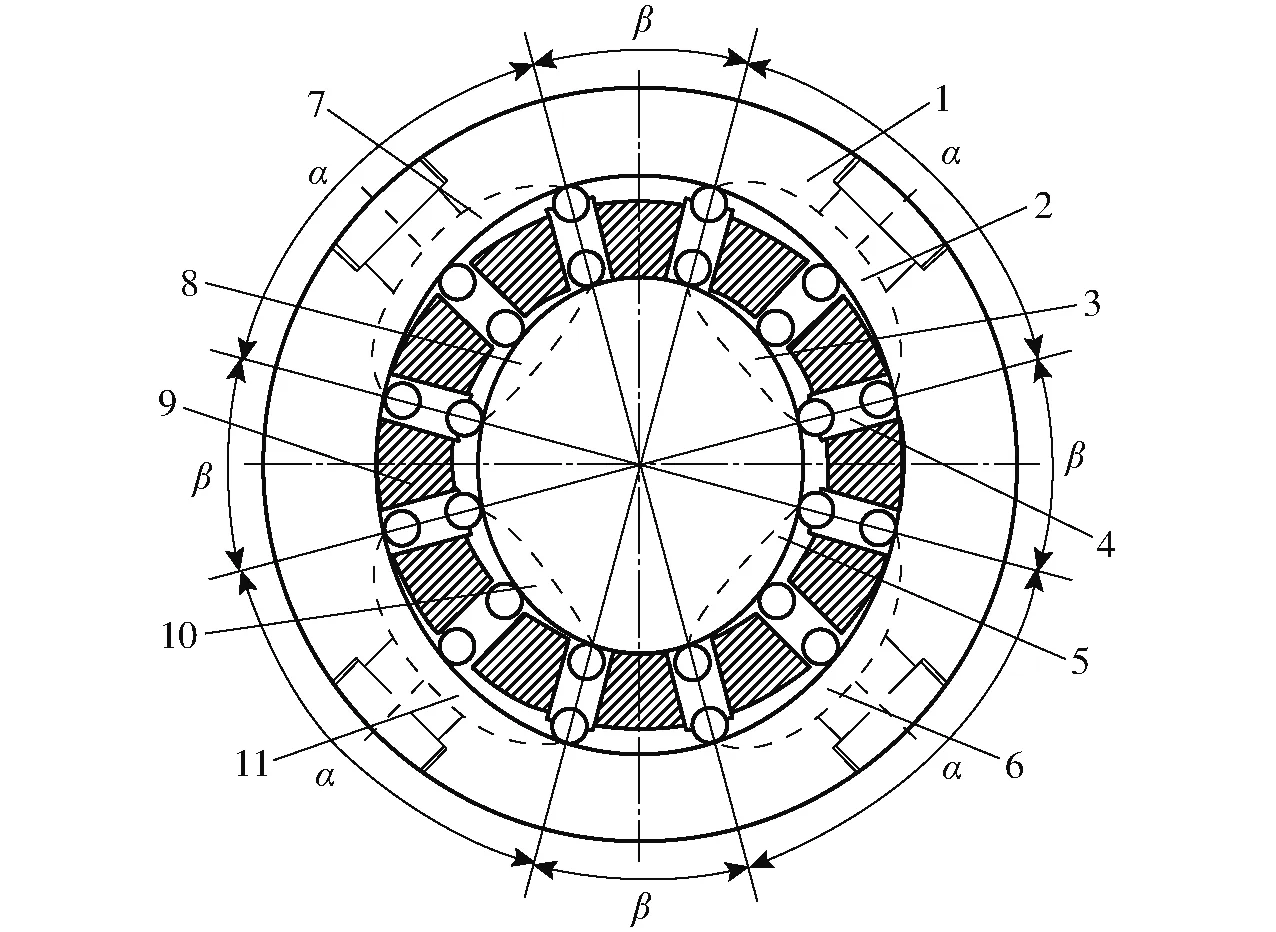
图1 双作用滚柱连杆式双定子马达原理简图Fig.1 Principle diagram of roller connecting bar double-acting double-stator motor1.外定子 2、11.外马达出油口 3、10.内马达进油口 4.滚柱连杆组 5、8.内马达出油口 6、7.外马达进油口 9.转子

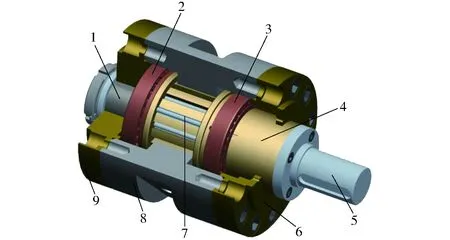
图2 马达三维结构图Fig.2 Three-dimensional structure of motor1.内定子 2、3轴承 4.转子 5.传动轴 6.左端盖 7.叶片 8.外定子 9.右端盖

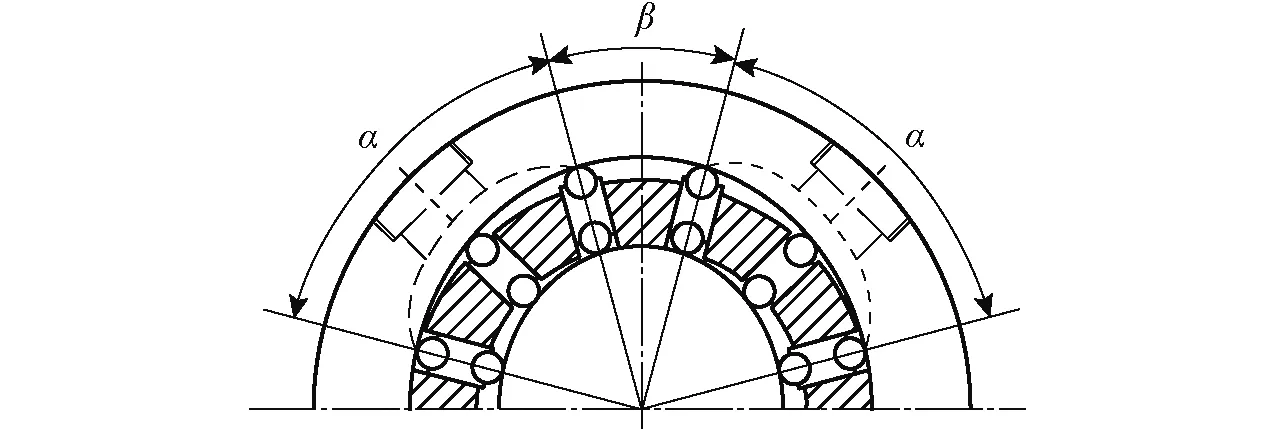
图3 外马达的通油流道分布Fig.3 Flow passage distribution of external motor

现有叶片式双定子马达的配流方式为：外马达为壳体配流，内马达为轴配流。其中外马达的油口结构及分布方式如图3所示，过油通道开设在过渡曲线区段的整个区间。由于两相邻滚柱连杆组间的区间角与大、小圆弧区的幅角相等，因此马达在工作的过程中也会像原有叶片马达一样存在高压回流冲击现象。

2 双定子马达预升压与预卸压

由闭死现象而引起的高压回流液压冲击以及突然泄压的现象会对叶片马达的正常工作造成极大的影响，但是闭死现象不可避免，否则叶片马达将无法正常运转。对双定子马达来说，消除配流过程中产生的油压冲击的方法之一就是进行预升压与预卸压。如图4所示，当两相邻的滚柱连杆组中的前一个进入大圆弧区段时，若此时让两相邻叶片间的工作腔不与大圆弧区段相连通，而是先转过一个角度之后再与大圆弧区段相连通，它们之间所组成的工作腔便处于机械封闭状态，体积开始增大，压力逐渐降低，在此作用下两相邻叶片间封闭的油液压力便可按照一定的规律下降，即当压力降至与出油口压力相等时，使其与大圆弧区段相连通，而在此过程中叶片转过的角度φ1称为闭死膨胀角。同理，预升压的过程中预先转过的角度φ2称为闭死压缩角。

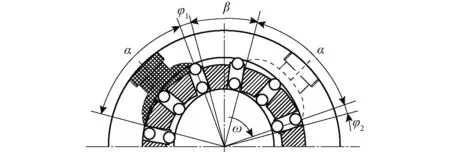
图4 改进配流通道的分布简图Fig.4 Distribution of improved channel assignment

对于外马达来说，大圆弧区两相邻叶片组成的工作容腔的油液初始体积为

(1)

式中Rw——外定子大圆弧半径，mm

R——转子外径，mm

s——滚柱连杆组厚度，mm

B——滚柱连杆组宽，mm

z——滚柱连杆组数

令工作腔在升压过程中由机械压缩引起的体积变化为ΔV1，则通过对封闭的油液体积进行压缩产生增大压力的效果，可表示为

(2)

其中

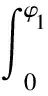
(3)

式中 Δp——双定子马达的额定工作压力，MPa

E——油液弹性模量

V——工作腔中油液初始体积

以等加速等减速过渡曲线为例进行计算，将其曲线方程代入式(3)可得

(4)

其中

式中A1——过渡曲线的系数

rw——外定子小圆弧半径，mm

ρ——等加速等减速曲线的矢径

α——定子曲线过渡区夹角

将式(4)代入式(3)并整理可得

(5)

同理可知处于外马达小圆弧区段相邻两叶片间的封闭油液初始体积为

(6)

则当处于小圆弧区段的两叶片转过闭死角φ2之后，两叶片间封闭油液的体积变化量为

(7)

将式(7)代入式(3)并整理可得

(8)

由式(5)与式(8)可以计算外马达的闭死压缩角与闭死膨胀角，从而实现双定子马达的预升压与预卸压以达到减小配流冲击的目的。

同理，可得出内马达的闭死膨胀角与闭死压缩角计算式为

(9)

(10)

其中

式中Rn、rn——内定子曲线大、小圆弧半径，mm

r——转子内径，mm

当双定子马达的各项结构参数及额定工作压力一定时，便可根据式(5)～(10)求解得到相应的闭死角。

由图3可知，当双定子马达通入高压油后，闭死容腔中的油液转过一个叶片厚度便进入进油区，工作腔中油液压力急剧上升，闭死容腔中的压力变化如图5所示。

图5 现有双定子马达工作腔中压力变化Fig.5 Pressure change in working chamber of existing double stator motor

3 三维模型与网格划分

首先运用三维软件建立双定子液压马达的外马达流体域模型(内马达分析过程类似，在此仅对外马达进行分析)，然后通过ICEM建立流体域网格模型，外马达流体域的三维模型和网格划分如图6所示。

为了实现对不同网格的单独控制，根据流体域的运动状态，将整体网格分割成为两个基本组成单元，分别为梯形块网格与滚柱网格，整体网格与局部放大网格如图7所示。

图6 三维模型与网格划分Fig.6 3D model and meshing

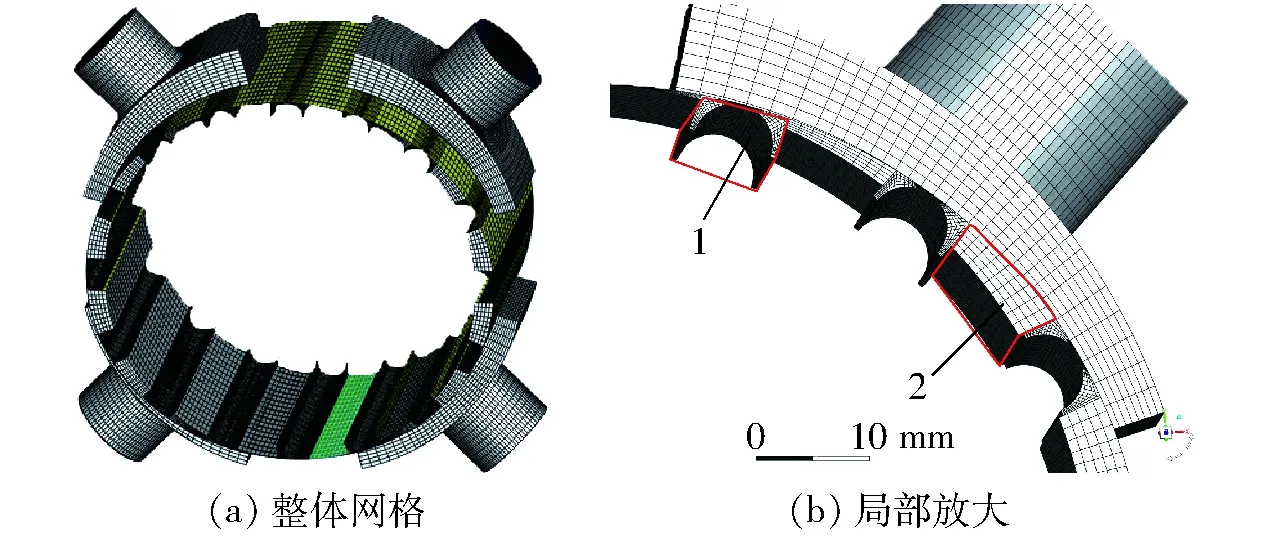
图7 整体网格与局部放大Fig.7 Overall grid and partial magnification1.滚柱网格 2.梯形块网格

通过UDF(user-defined-function)分别控制梯形块网格的外表面，滚柱网格的外表面及滚柱网格的内表面运动，以模拟流体域的变化。其中梯形块网格与滚柱网格外表面采用GRID_MOTION用户自定义宏对表面上每个点进行运动控制，滚柱内表面采用CG_MOTION用户自定义宏对内表面网格整体进行刚性运动控制。

3.1 梯形流体域网格外表面的运动控制

首先通过三维软件确定梯形块网格外表面与内表面两连线交点位置，作为初始值，交点位置及编号如图8所示，坐标值如表1所示。

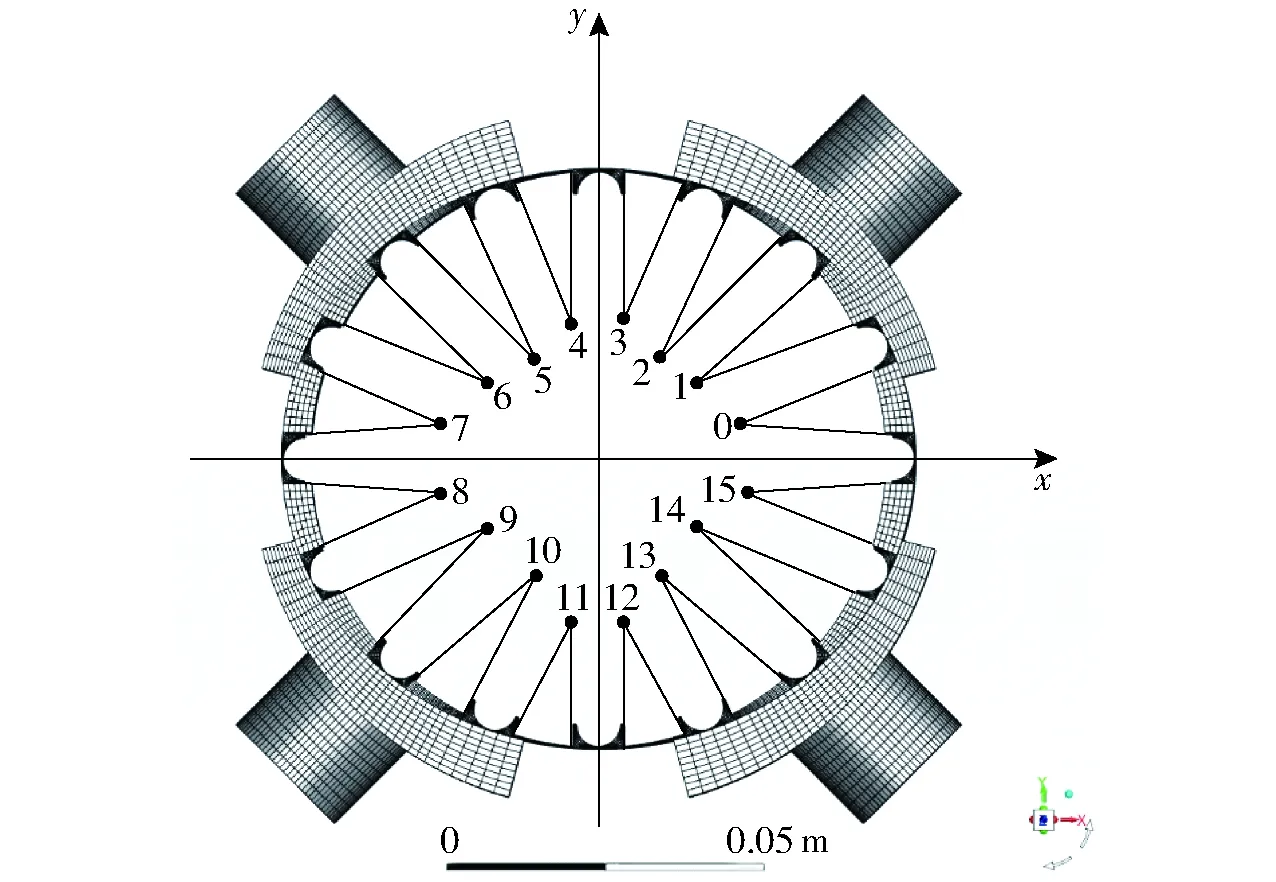
图8 梯形流体域的两侧面连线交点位置示意图Fig.8 Intersection of two sides of trapezoidal fluid domain

3.2 滚柱网格外表面的运动控制

滚柱网格外表面与梯形块网格的外表面运动相似，不同之处在于滚柱网格中没有两侧面交点。因此本文首先通过三维软件获得坐标原点与滚柱圆心连线与定子曲线交点坐标，作为初始值，位置及编号如图9所示，坐标值如表2所示。

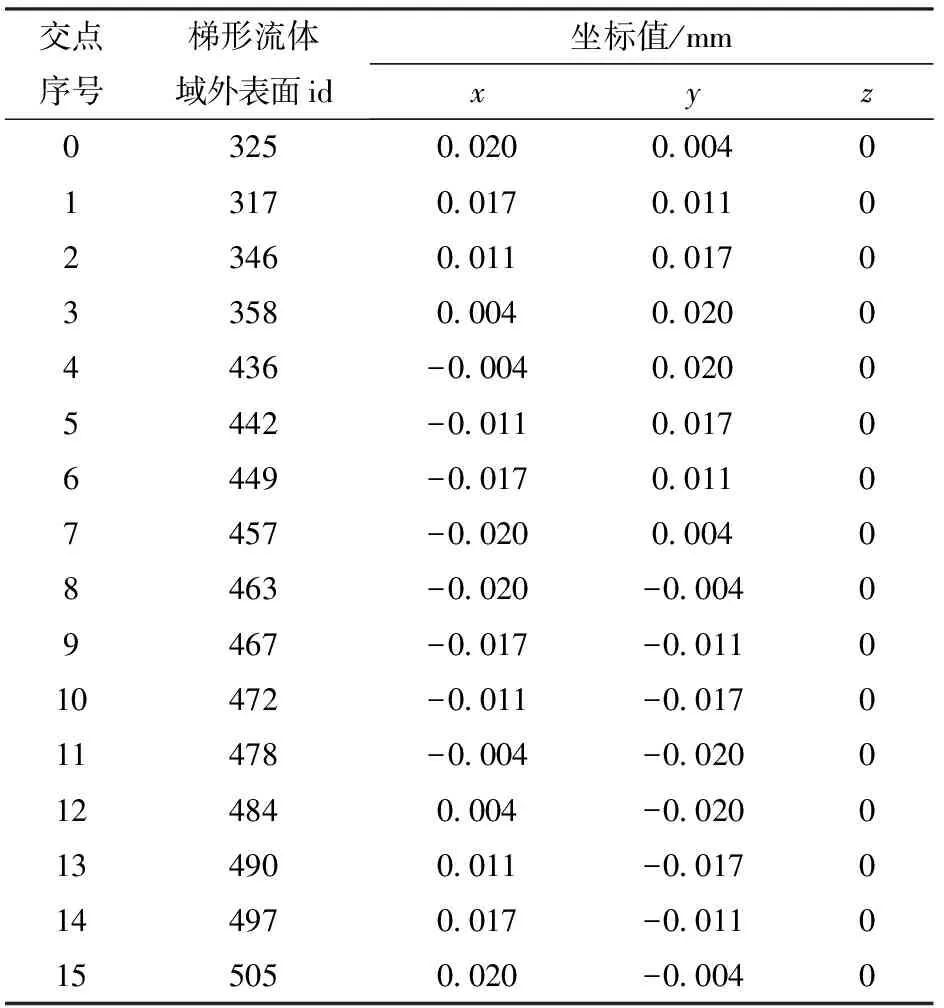
表1 梯形流体域的两侧面连线交点坐标Tab.1 Intersection coordinates of two sides of trapezoidal fluid domain

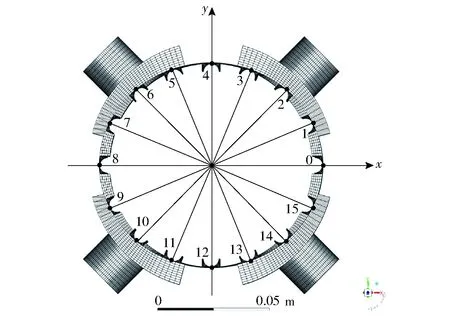
图9 滚柱流体域编号示意图Fig.9 Roller fluid domain numbering diagram

梯形块网格与滚柱网格及配流通道网格间通过滑移网格实现连接，由于网格弹性光顺过程中表面网格涉及两次旋转变化，再加上运动不规律，滑移交界面处网格再变形尺度较大后将产生法向变形，进而引起网格失败。因此需要在网格交接面处设置geom以限定滑移交界面处网格不产生法向运动。

4 模型的边界条件与求解控制

采用SIMPLE(Semi-implicit method for pressure linked equations)算法，基于压力的速度分离求解算法的求解迭代过程如图10所示，控制算法中调用的C语言程序函数如图11所示。

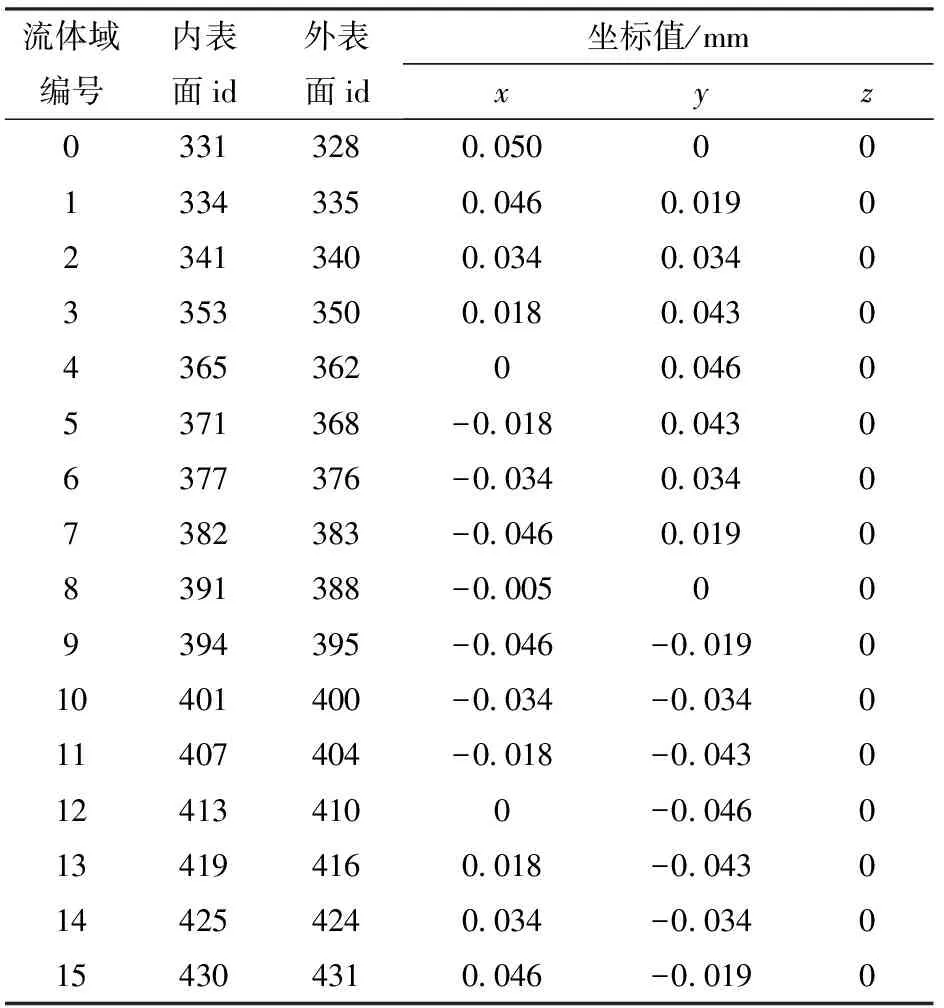
表2 坐标原点与流体域圆心连线与定子曲线交点坐标Tab.2 Coordinate of intersection of coordinate origin and center of fluid domain with coordinates of stator curve

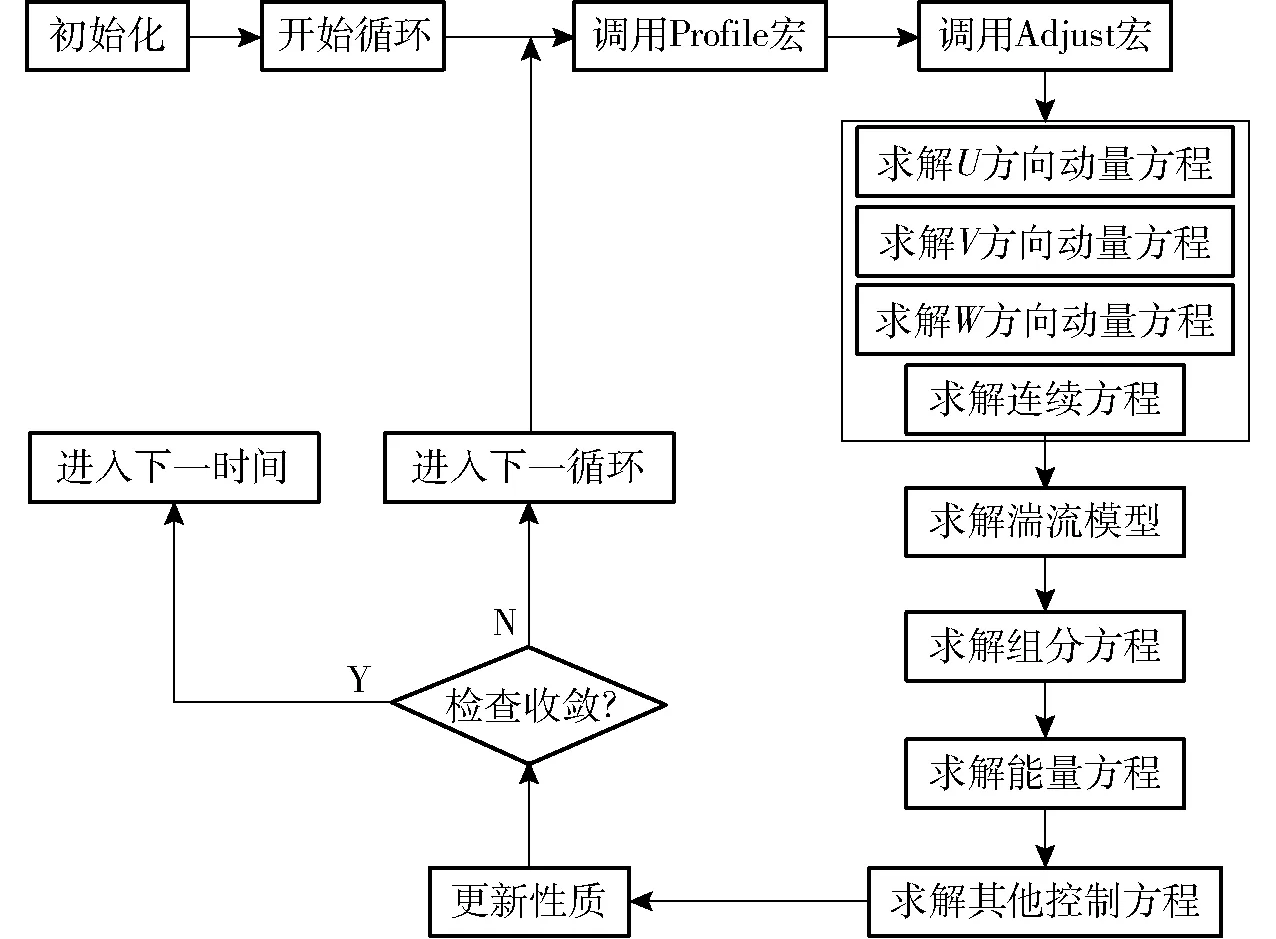
图10 AMG求解器迭代过程Fig.10 AMG solver iterative process diagram

图11 控制算法调用的C语言程序函数Fig.11 C program function called in control algorithm

基于压力的求解过程在进行求解域离散化之后，将确定求解方程，包括动量方程、连续方程、能量方程与状态方程。通过宏命令DEFINE_PROFILE、DEFINE_INIT、DEFINE_PROPERTIES初始化求解域，完成后准备进行迭代求解。在每一个循环开始前，都可以通过宏命令DEFINE_PROFILE、DEFINE_ADJUST对求解域进行一系列需要的操作，包括调整求解域内变量值，进行数值积分等。在迭代求解收敛候通过C语言编写的动网格宏命令，控制求解域进行相应的结构变化，进行下一次求解器迭代过程，直至达到设置的网格运动收敛条件。

流体域入口边界条件为压力入口，出口边界条件为压力出口，基本网格单元之间的交界面为滑移交界面，壁面为无滑移壁面。模型采用SSTk-ω湍流模型，流体模型为不可压缩，密度为840 kg/m3，动力粘度为0.027 7 Pa·s。采用SIMPLE算法求解基本控制方程与湍流模型方程，在迭代周期中将调用通过C语言编写的程序以实现对网格运动变形的控制和检测流体域的瞬时压力。时间离散步长为10-5s，收敛标准设定为残差低于10-4。通过调节欠松弛因子，每个时间步长内收敛的迭代计算循环在20左右。瞬态计算的残差曲线如图12所示。

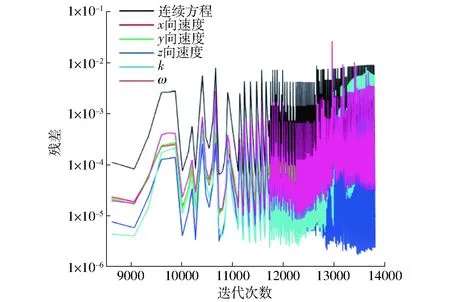
图12 瞬态计算的残差曲线Fig.12 Transient calculation residual curves

5 模型求解结果

通过以上算法能够实现双定子液压马达瞬态计算过程中流体域的变化。不同时间节点的网格模型以及压力云图如图13～15所示。

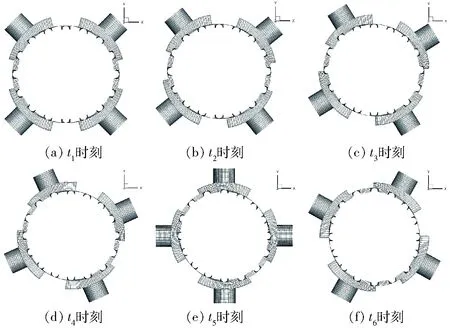
图13 流体域在不同时刻节点的网格模型Fig.13 Grid models of fluid domains at different time nodes

从图14、15可以看出，外马达闭死容腔中的压力在随马达旋转的过程中均平滑过渡。因此，通过开设闭死压缩角与闭死膨胀角可以在一定程度上改善双定子液压马达的高压回流与突然卸压的问题。

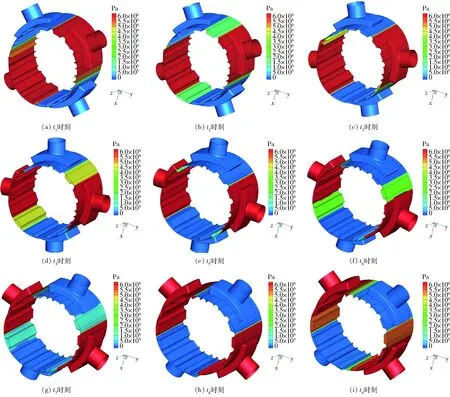
图14 进口压力边界6.3 MPa、转速1 000 r/min时的压力云图Fig.14 Pressure cloud diagrams at inlet pressure boundary of 6.3 MPa and 1 000 r/min

为了更清楚地观测流体域在经过闭死容腔时的瞬时压力变化情况，分别对图16所示的两个梯形块流体域在两种条件下的压力进行检测，并得出两个位置的瞬时压力变化曲线如图17所示。

从图17可以看出，位置1的流体域在随着马达的旋转而逐渐进入闭死容腔，随后又经过马达出油口的过程中，其压力变化先逐渐升高而后基本保持与马达出油口的压力一致。位置2的流体域随着马达的旋转而逐渐进入闭死容腔，随后在经过马达进油口的过程中，其压力先逐渐降低而后基本保持与马达进油口的压力一致。此外两个位置的瞬时压力变化均平滑过渡，基本没有出现压力突变的现象。

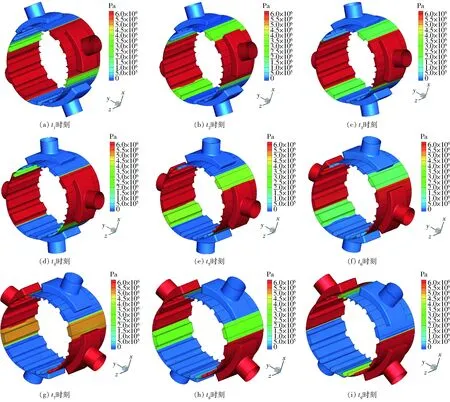
图15 进口压力边界6.3 MPa、转速1 500 r/min时的压力云图Fig.15 Pressure cloud diagrams at inlet pressure boundary of 6.3 MPa and 1 500 r/min

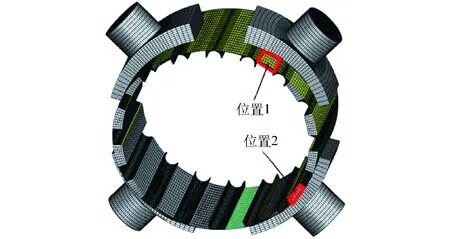
图16 两个压力监测点的位置Fig.16 Position of two pressure monitoring points

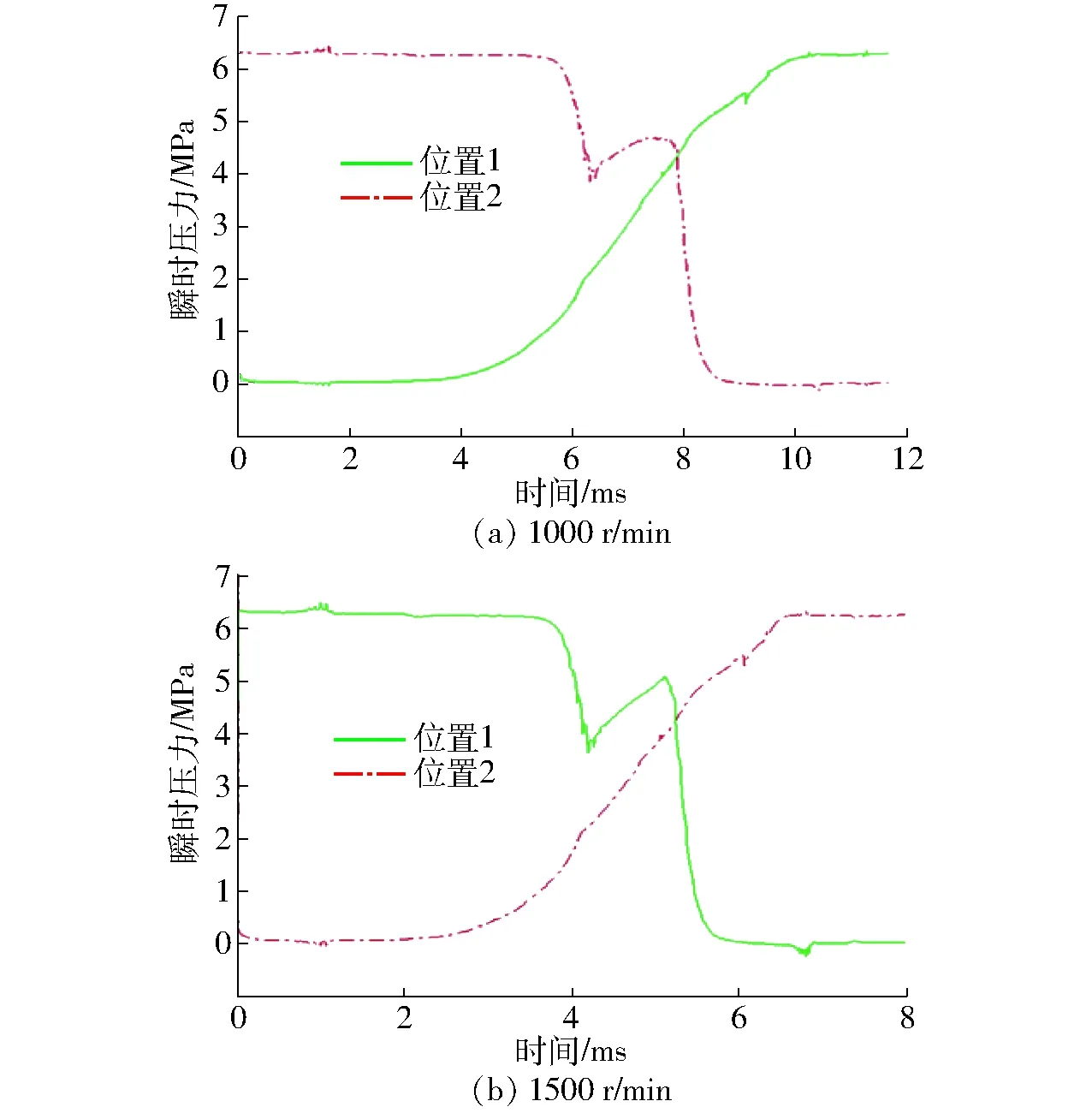
图17 瞬时压力变化曲线Fig.17 Instantaneous pressure curves

在CFD模型的建立过程中，采用了SSTk-ω模型，其适合从高雷诺数流动到低雷诺数的流动问题。计算过程中，为了保证准确性，采用了很小的时间离散步长(10-4)与较高的收敛精度(10-5)。同时，还进行了网格独立性研究，计算了网格数为3×104、6×104、1.2×105、2.1×105、3×105的模型，结果表明网格数由2.1×105增至3.0×105时，压力变化已经不明显，因此该结果独立于网格数量。

6 结论

(1)配流冲击是双定子马达的主要噪声源之一，在双定子马达的配流机构上开设闭死角，可以使闭死容腔中的油液压力过渡到与其接通油腔的油液压力相等时再接通，从而消除配流冲击，有效降低马达的振动与噪声，提高马达效率、可靠性和寿命。

(2)合理设计闭死角，能够使闭死容腔中油液压力变化曲线平滑过渡，即缓慢升高至额定压力、缓慢降至出油口油压，有效地解决了压力突变的问题，避免了双定子马达的高压回流与突然卸压的现象。