基于唯一域方法的机器人逆向运动学求解
李 光 肖 帆 杨加超 章晓峰 马祺杰
(湖南工业大学机械工程学院, 株洲 412007)
0 引言
机器人逆运动学求解是机器人离线编程、轨迹规划、控制算法设计等其他课题研究的基础[1]。逆运动学求解的实质是完成机器人工作空间到关节空间的映射,逆运动学方程组具有高维、非线性的特点,求解复杂且不易求出[2]。很多学者在该领域做了大量研究,提出了许多理论与方法。传统方法有代数法[3]、几何法[4]和数值法[5]等。代数法主要以消元的方式,将机器人位置反解中的高维方程组简化为低维方程组,从而求得所有逆运动学解。该方法需要进行大量的三角代换,简化过程十分复杂,HUSTY等[6]认为求解非线性代数方程往往需要靠直觉甚至运气才能获得。几何法针对机器人的某些特殊结构进行简化,再进行求解,一般无法单独使用,甚至根本无法使用[7]。数值法的求解速度与初始值相关。
随着计算机技术的快速发展,许多学者将智能优化方法应用于机器人逆运动学问题[8-11]。文献[8-11]的方法均属于进化算法的范畴,其迭代过程中不受梯度和初始值的影响,具有通用性,但无法有效求得机器人所有逆运动学解。文献[12-13]将关节空间划分为多个子空间,采用多神经网络的方式,分别求得了平面2R机械手和空间3R机械手的逆运动学多解,但是均未提出一种划分关节空间的通用方式。
RASTEGAR等[14]提出利用det(J)=0(J为雅可比矩阵)方程,将非冗余机器人关节空间划分为与逆解数目相同的唯一域,再在每个唯一域中用数值法迭代求解,进而求得所有逆运动学解。其思路可行,因MANOCHA等[15]举例说明在某种情况下6自由度机器人的逆解问题有16个实数解,并确定解的数目上限为16;WENGER[16-17]进一步完善了利用det(J)=0划分唯一域的条件。
在det(J)=0划分唯一域的理论指导下,MOULIANITIS等[18]使用48个多层感知器近似求解了KUKA 7自由度仿人臂前6个关节的逆运动学多解(文中所提的KUKA机器人为该款机器人);周枫林等[19]用多模块RBF神经网络求解了PUMA560机械手前3个关节的逆运动学多解。然而,神经网络需要大量的样本进行训练,无法保证求解的实时性;同时,样本的数量和分布会影响训练好的神经网络的泛化精度,并且位于奇异点附近的样本,神经网络无法直接训练。
本文将方程det(J)=0作为划分6自由度机器人关节空间的依据,将各个唯一域的边界作为约束条件,采用协方差自适应矩阵进化策略(Covariance matrix adaptation evolution stategy,CMA-ES)[20]对6自由度机器人进行有约束寻优;使用佳点集方法产生初始搜索点,从而求得所有逆运动学解。在钱江一号6R工业机器人和KUKA仿人机械臂上进行仿真实验。
1 6R机器人唯一域的确定
文献[17]将非冗余机器人分为了尖面机器人(Cuspidal robot)和非尖面机器人(Noncuspidal robot),在非尖面机器人中可以直接采用det(J)=0方程划分唯一域。图1为非尖面6自由度机器人划分唯一域求逆解的方法流程图,Qn为唯一域中的逆运动学解,其中n≤16。
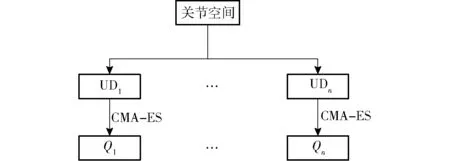
图1 非尖面6R机器人逆运动学求解流程图Fig.1 Flow chart for solving inverse kinematics of noncuspidal 6-DOF robot
由于非尖面6自由度机器人的结构不同,最终划分唯一域的方法也会有所差异。为了能详细地阐述本文所提的方法,以工业6R机器人为例进行详细说明。
1.1 6R工业机器人正向运动学及适应度函数
图2是钱江一号6R工业机器人[21]以D-H法建立的连杆坐标系,表1是其D-H参数,其中a1=150 mm,a2=550 mm,a3=160 mm,d4=594 mm,机器人零位是关节3以括号内的角度旋转后所得。
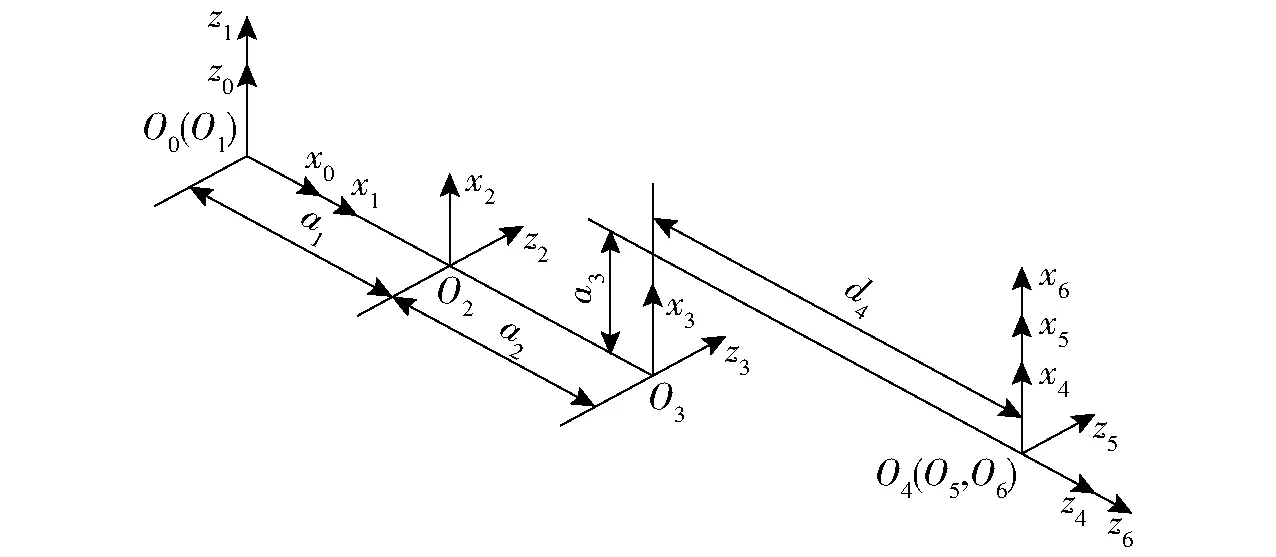
图2 钱江一号机器人连杆坐标系Fig.2 Linkage coordinate system of Qianjiang No.1 robot
机器人连杆{i}坐标系相对于{i-1}坐标系的变换矩阵为
(1)
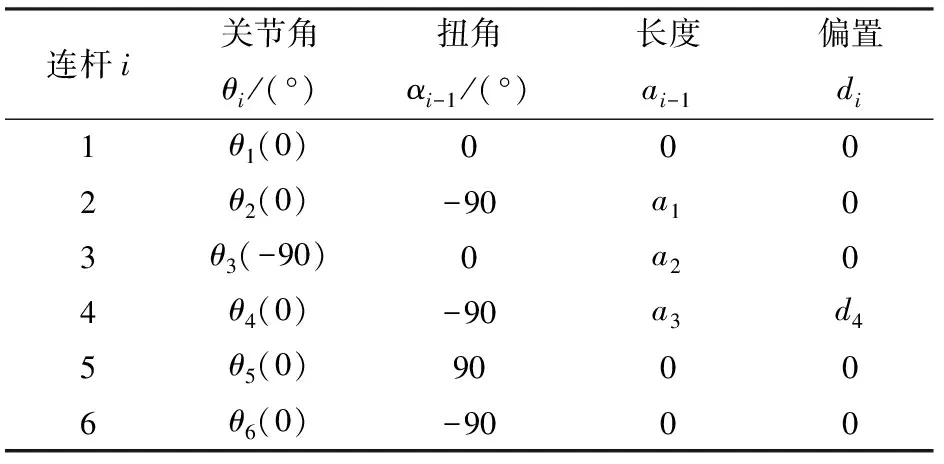
表1 钱江一号机器人的关节参数Tab.1 Joint parameters of Qianjiang No.1 robot
其中,sθi、cθi、sαi-1和cαi-1为sinθi、cosθi、sinαi-1和cosαi-1的简写形式。已知机器人的关节向量θ=(θ1,θ2,θ3,θ4,θ5,θ6),根据式(1)和表1中的D-H参数,得到机器人腕部相对于基坐标系的位姿矩阵
(2)
机器人手腕的位置由前3个关节可以完全确定,其姿态最终由后3个关节确定,所以采用臂腕分离的方式建立适应度函数
fitness1=‖pdes-pcur‖
(3)
fitness2=‖ades-acur‖
(4)
式中fitness1——目标位置pdes与实际位置pcur之间的误差
fitness2——目标接近矢量ades与实际接近矢量acur的误差
其中接近矢量与θ6无关,如需要求解的机器人不能臂腕分离求解,则适应度函数可参照文献[7],用位置误差和姿态误差加权和的形式表达。由于姿态是建立在前3个关节基础上得到的,所以可以先用式(3)求解θ1、θ2、θ3,然后代入式(4)求θ4、θ5。θ6可将求得的前5个关节角作为已知条件,联立oz、nz求解,即
(5)
其中
A=s23sinθ5-c23cosθ4cosθ5
B=c23sinθ4
式中c23、s23分别表示cos(θ2+θ3)、sin(θ2+θ3)。
1.2 唯一域划分
通过微分法[22]在Matlab中计算,求得机器人的雅可比矩阵行列式为
det(J)=Pn1Pn2Pn3
(6)
其中
Pn1=a2sinθ5
Pn2=a3cosθ3-d4sinθ3
Pn3=a1+d4c23+a3s23+a2cosθ2
由式(6)可以看出,工业机器人的奇异性只与关节2、3、5有关。
Pn1和Pn2分别只与θ3、θ5有关,可直接求出θ3、θ5的值作为边界:θ3的边界分别为-2.940 8 rad、0、3.342 4 rad;θ5的边界分别为-π、0、π。Pn3不方便求解,可直接作为非线性约束条件。根据1.1节中适应度函数的构造,θ2和θ3所划分的唯一域只与fitness1有关,令f=Pn2Pn3,可在θ2和θ3组成的平面内进一步研究f=0时唯一域的划分。
图3中绿色线为θ2和θ3平面内的奇异轨迹线,在上半区θ3∈[0.200 8,3.342 4] rad,Pn3≤0的部分组成了UD1,Pn3≥0的部分组成了UD3;在下半区θ3∈[-2.940 8,0.200 8] rad,Pn3≤0的部分组成了UD2,Pn3≥0的部分组成了UD4。如果没有限制θ2,则沿θ2轴的方向上,每个唯一域都会有无数种解,因为根据三角函数知识,θ2与2kπ+θ2(k∈Z)对应的三角函数值相等,所以选择唯一域时,可以根据图3适当调整θ2的边界,使得边界内包含一个完整的UDi(i=1,2,3,4)即可,如图4红色区域,图中各区域的边界条件见表2。
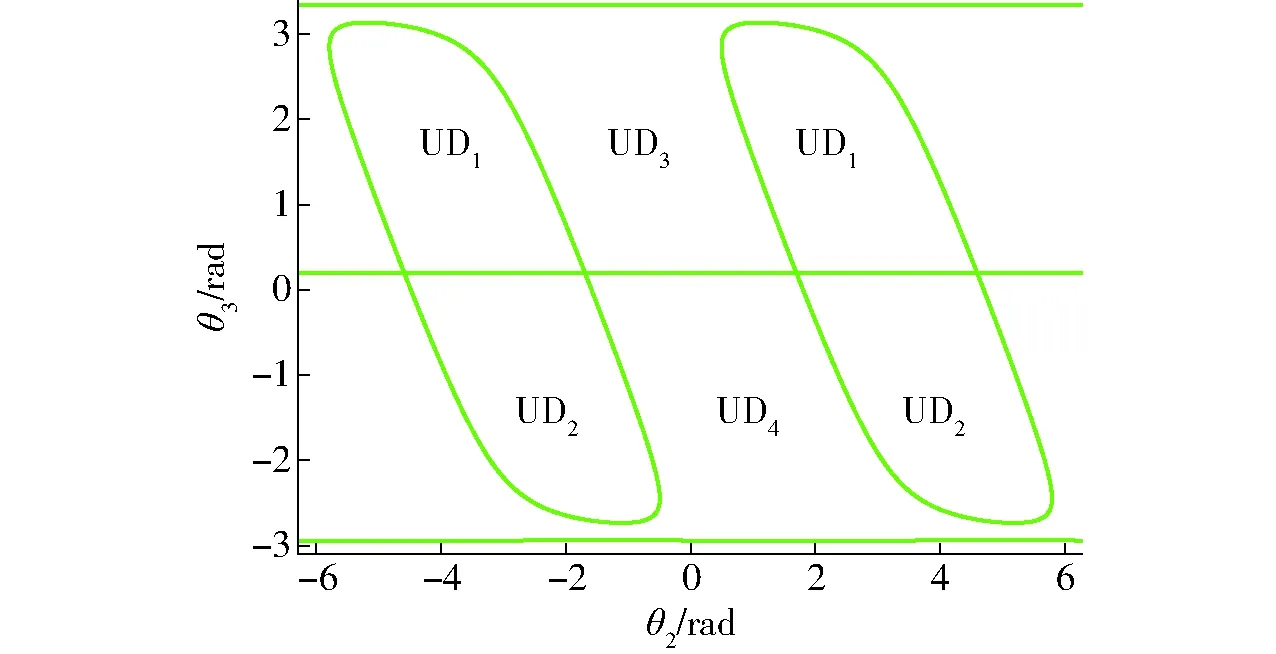
图3 唯一域划分Fig.3 Uniqueness domains division
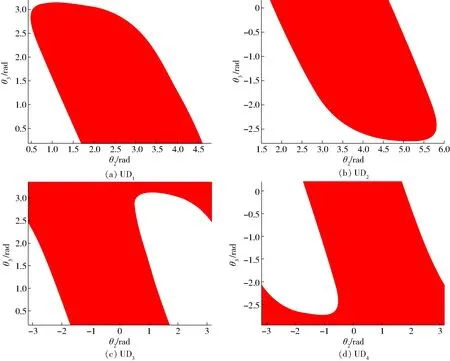
图4 θ2和θ3间的唯一域划分Fig.4 Uniqueness domains partition between θ2 and θ3
又因为θ5将[-π,π]以0为界划分成了2个唯一域,与UDi(i=1,2,3,4)可以组合得到8个唯一域,记为UDij(j=1,2),如图5所示,图中“+”表示组合。
2 基于CMA-ES算法的逆运动学求解
2.1 CMA-ES算法原理
CMA-ES算法的本质属于进化策略类算法。经典进化策略算法主要依赖于突变来寻找最优解,而突变方向需要依据经验设置,以该方法调整会导致无效的突变,进而浪费计算成本。为克服经典进化策略的局限性,CMA-ES采用多维正态分布N(m,C)产生搜索种群,m代表种群分布的中心;C是协方差矩阵且对称正定,对其特征分解可得C=BDBT,其中BBT=I,B的列向量由C的特征向量正交基组成,D为对角阵,对角元素是C矩阵特征值的平方根。
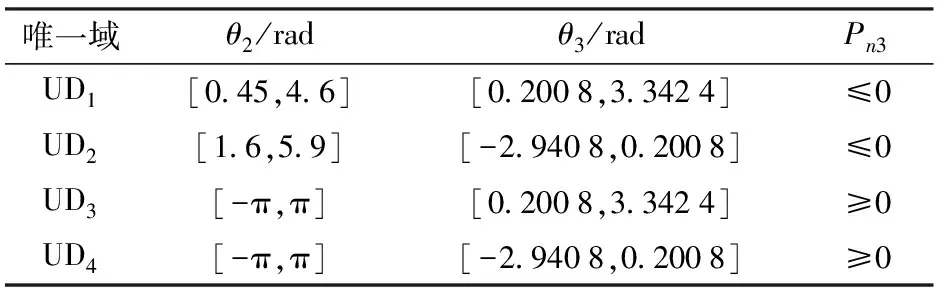
表2 各唯一域确定条件Tab.2 Uniqueness domains determination conditions
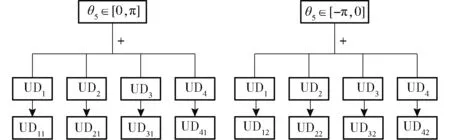
图5 8组唯一域组合方式Fig.5 Eight groups of uniqueness domains combinations
CMA-ES算法实现步骤如下[23-25]:
(1)参数设置及初始化。静态参数:种群大小λ,父代个体数为μ<λ,重组权值ωi(i=1,2,…,μ),以及自适应调整时所需的常量cσ、dσ、cc、c1、cμ、μeff,最大迭代次数为G。动态参数:初始分布均值m∈RN(N是问题维数),全局步长σ∈R+,进化路径pσ=0,pc=0,协方差矩阵C=I,迭代次数g=0。静态参数的计算公式见文献[25]。
(2)抽样。通过对多元正态分布进行抽样生成搜索种群,抽样公式为
yk=BDN(0,I)~N(0,C)
(7)
xk=m+σyk~N(m,σ2C)
(8)
式中xk——种群的第k个个体
yk——均值为0的多元正态分布
(3)优选重组,即均值更新,具体计算公式为
(9)
(10)
其中
式中xi:λ——种群排名第i的个体
对于最小化问题,其排名由目标函数从小到大的排序决定。
(4)步长控制。首先更新步长进化路径pσ,即
(11)
式中μeff——方差有效选择质量,且1≤μeff≤μ
步长σ的更新公式为
(12)
式中dσ——接近1的阻尼系数
E‖N(0,I)‖——正态分布随机向量范数的期望
(5)协方差矩阵调整。更新进化路径
(13)
式中hσ是Heaviside函数,可以在‖pσ‖较大时使pc更新停顿,从而避免协方差矩阵C在线性环境中轴线过快增长。协方差矩阵的调整公式为
(14)
其中
δ(hσ)=(1-hσ)cc(2-cc)
式中c1——C的秩为1的更新学习率
cμ——C的秩为μ的更新学习率
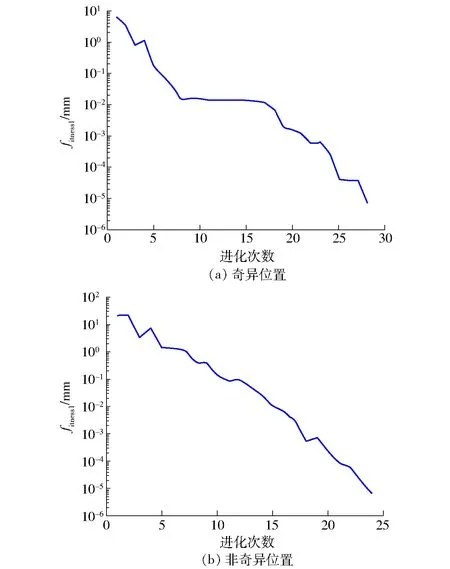
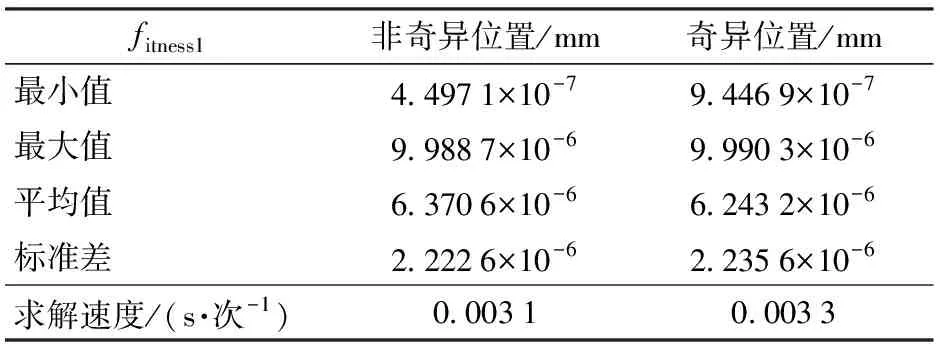
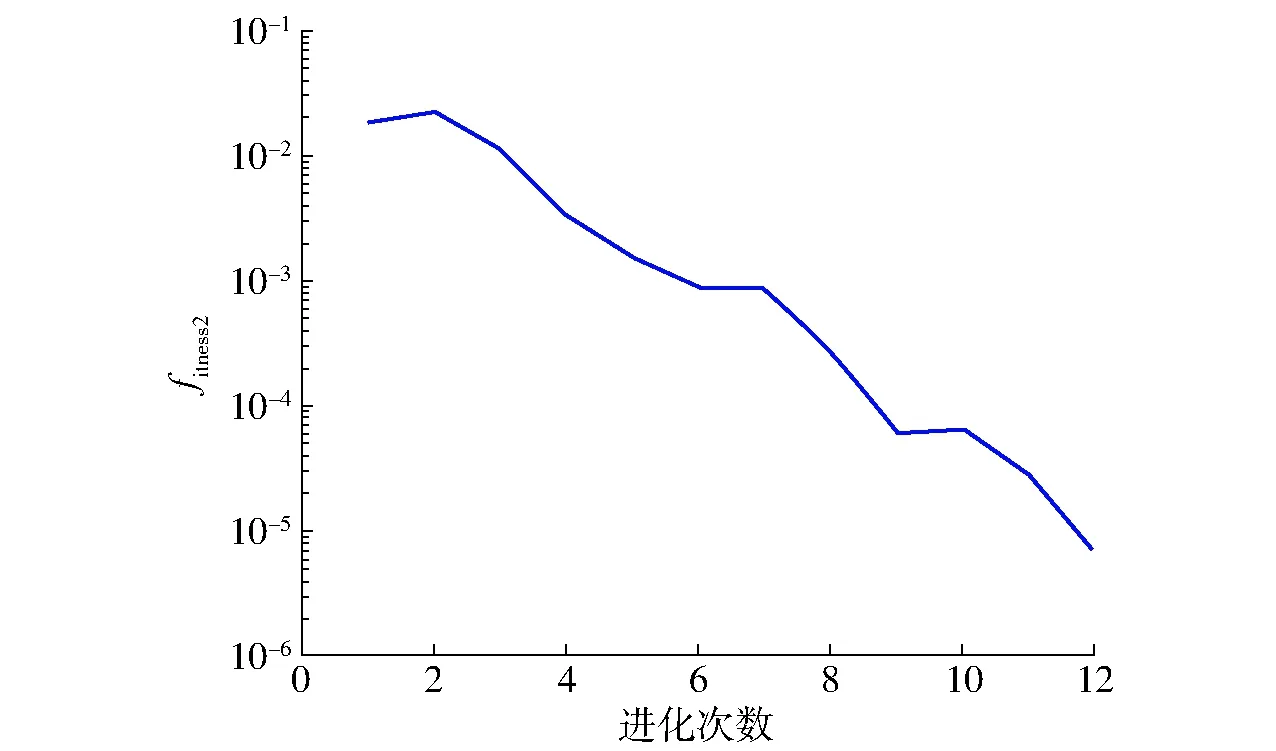
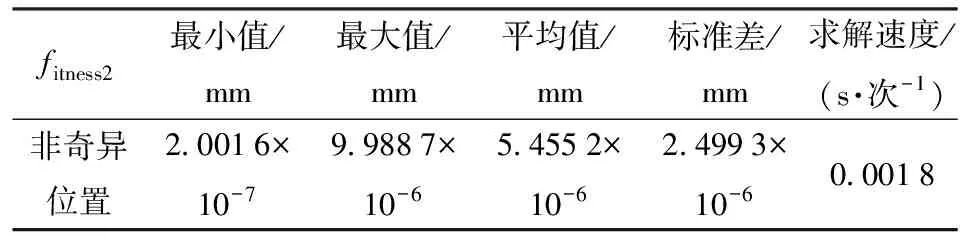
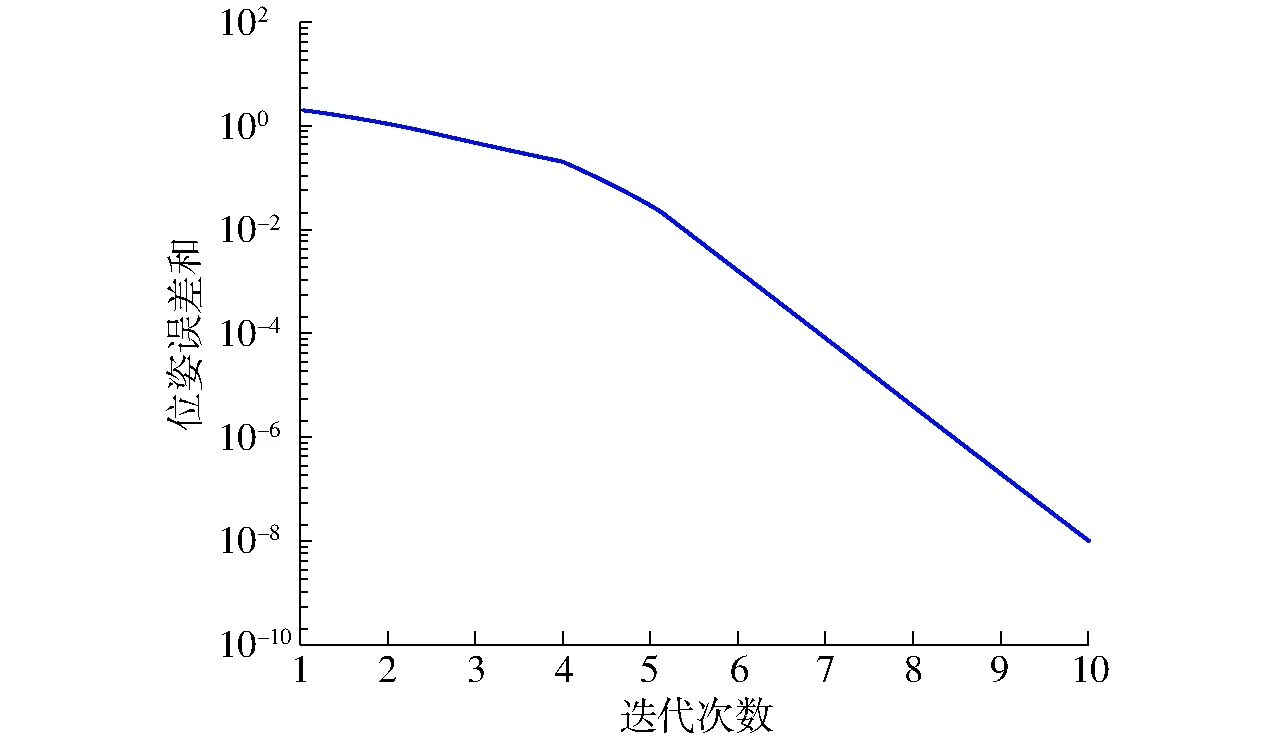
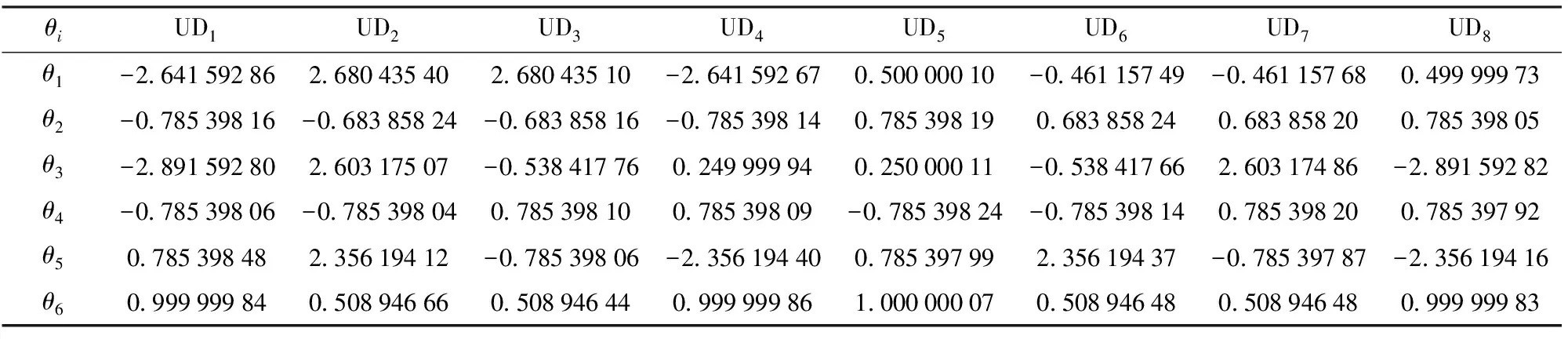
(6)终止判断。若g 步骤(5)中,协方差矩阵C结合了秩μ、秩1更新率,前者可以充分利用当前代的信息,后者利用了代与代之间的信息,二者的有机结合,避免了算法求解精度上对种群大小的过分依赖,以及进化过程中种群“早熟”的问题;同时引入进化路径来引导种群的寻优搜索,提高了算法的寻优效率和可靠性。C的更新机制,使得算法在寻优过程中具有确定性。 图6为CMA-ES算法的进化过程,其中“★”表示种群的均值,“●○”表示种群中所有个体,“●”表示种群中前μ个优秀个体,“▲”表示最优值,虚线为种群分布形状。可以看出种群的进化过程随着优秀个体的引导接近最优值。 图6 CMA-ES进化过程简示图Fig.6 Simplified diagram of evolution process of CMA-ES 原始的CMA-ES算法初始均值点随机产生,从第1节唯一域的划分可以获知,随机产生的均值点,可能不在需要求解的唯一域内。同时在每个唯一域内适应度函数都是单峰函数,如果均值点在每个要求解的唯一域内,并且接近峰值,则可以大大地缩小算法的搜索时间。实现初始均值点的产生步骤如下: (1)采用佳点集[26]方法获得分布于唯一域边界条件内的均匀点集,记为Pb。 (2)如果求fitness1,则将Pb中的θ2和θ3代入第1节中的Pn3,根据Pn3大于(或小于)0筛选符合唯一域内的点集,并记为PU;如果是求fitness2,则跳过此步骤。 (3)如果求fitness1,将PU代入适应度函数,选择其中使得适应度最小的点作为初始均值点;如果求fitness2,则将本步骤中方法的PU改为Pb。 佳点集计算公式[27]为 rk=ek(1≤k≤t) (15) Pbi(k)={{r1i},{r2i},…,{rti},i=1,2,…,n} (16) 式中t——维数 {rki}——rki的小数部分 Pbi(k)中每个维度都在[0,1]内,可以映射至搜索空间,即 (17) 从表2可看出,θ2和θ3不全部位于[-π,π]之间,可对求得的逆运动学解进行转换:如θi>π,则θi=2π-θi;如θi<-π,则θi=2π+θi;否则θi不变,i=1,2,…,6。 将进行两个仿真算例,算例1求本文所提的工业机器人的8组逆解;算例2求文献[18]中仿人臂前6个关节组成的6R机械臂的8组逆解。每个案例中都将用本文所提方法与文献[5]所提的数值法进行比较。 用于仿真的计算机配置如下:操作系统为64位Windows 7专业版,处理器为IntelCore i3-6100,CPU速度为3.70 GHz,安装内存为8.00 GB;仿真计算软件为Matlab 2016a。 先在工业机器人唯一域UD31中,利用式(3)与CMA-ES算法分别对奇异点和非奇异点求逆解;然后将求得的非奇异位置作为已知条件,用式(4)与CMA-ES算法求解θ4和θ5;最后求出所有唯一域中的逆运动学解。数值法采用CMA-ES算法的初始值进行迭代,直接求UD31非奇异位置的6个关节角。 3.1.1参数设置 θ1、θ4、θ6的取值范围均设为[-π,π]。佳点集的点数n设为800,CMA-ES算法中的种群数λ=100,优秀个体数μ=50,初始步长σ=0.1,终止条件为G=100,或者fitness1(fitness2)<10-5mm;数值法的步长α=0.95,终止条件G=100,或者位姿误差和Eerr<10-5mm。 3.1.2UD31中仿真结果 分别取非奇异位置的关节角Q1=[1,-1.2,2.2,0.5,-1,2]rad和奇异位置关节角Q2=[1,-2.465 226 450 132 348,1.564 034 453 319 104,0.5,-1,2]rad,代入正向运动学式(2),得到位姿T1、T2,然后在唯一域条件下,分别用CMA-ES算法对T1、T2的位置单独求解1 000次。 图7和表3是CMA-ES算法对位置求解的结果,可以看出CMA-ES算法在奇异位置和非奇异位置上的求解误差和速度总体相差不大,适应度函数几乎呈线性收敛。 图7 UD31中CMA-ES单次求解进化过程Fig.7 Single-time evolution of CMA-ES in UD31 图8和表4为求出的T1前3个关节角作为已知条件求解UD31的θ4和θ5,由于只搜索两个关节角,所以算法收敛迅速,求解速度比位置求解快将近一 表3 UD31中CMA-ES独立运行1 000次的fitness1结果Tab.3 fitness1 results for CMA-ES running independently 1 000 times in UD31 图8 CMA-ES单次求解θ4和θ5进化过程Fig.8 Single solution of θ4 and θ5 evolutionary processes by CMA-ES fitness2最小值/mm最大值/mm平均值/mm标准差/mm求解速度/(s·次-1)非奇异位置2.0016×10-79.9887×10-65.4552×10-62.4993×10-60.0018 倍。θ6是代数公式求解,其速度为10-4ms/次,可以忽略不计。 图9是数值法求T1逆解的迭代过程图,从图中可以看出,收敛速度很快,并且每次求解都收敛于7.08×10-7,独立运行1 000次测出的求解速度为7.5 ms/次。 图9 数值法迭代过程Fig.9 Numerical method iterative process 从数据对比可以看出,在6R工业机器人逆运动学求解中,CMA-ES算法的求解稳定性与精度比数值法稍微逊色,但求解时间优于数值法,CMA-ES算法求一组逆运动学平均求解时间约5.1 ms/次。 对文献[18]中KUKA机器人的前6个关节求逆运动学多解。通过该机器人的雅可比奇异方程,可以直接求出θ2、θ4和θ5(表5),所以唯一域可以直接由边界的方式划分,划分方法参照第1节。CMA-ES的适应度函数为位置与姿态的加权和[7],位置误差的加权系数为0.004,姿态误差的加权系数为1,θ1、θ3和θ6的取值范围均为[-π,π]rad。将Q3=[0.5,π/4,0.25,-π/4,π/4,1]rad代入式(2)得到目标位姿T3。 在唯一域UD1中对CMA-ES和数值法进行求解对比,结果见表6。 表5 KUKA机器人的唯一域Tab.5 Uniqueness domains of KUKA robot rad 从表6可以看出,在KUKA机器人逆运动学求解中,CMA-ES算法的稳定性与精度同样稍逊于数值法,求解速度却快了将近3倍。表7、8为两款机器人的8组逆解,各关节角均转换至[-π,π]。 表6 UD1中CMA-ES独立运行1 000次的绝对位置误差Tab.6 Absolute position error for CMA-ES running independently 1 000 times in UD1 表7 工业机器人的8组逆运动学解Tab.7 Eight solutions of inverse kinematics of industry robot rad 表8 KUKA机器人的8组逆运动学解Tab.8 Eight solutions of inverse kinematics of KUKA robot rad 从两个算例可以看出,在满足精度要求的前提下,CMA-ES算法的求解速度明显优于文献[5]所提的数值法。 KUKA机器人中的逆运动学求解速度比工业机器人求解速度慢,主要因为该机器人无法臂腕分离,从而增加了算法的搜索维度,进而增加了求解过程中的时间消耗。经测算,CMA-ES算法中68%~74%的时间消耗用于适应度函数计算,如果可以加快该算法适应度函数的计算,则其求解速度将会得到显著提高。同时,CMA-ES算法的原理导致其进化过程中,会向不可行域探索,从而在进化中产生无效搜索,如果在这一方面也进行改进,则求解速度将会有所提高。 (1)利用det(J)=0及图像可视化方法,将钱江一号6R工业机器人的关节空间划分为8个唯一域,缩小了CMA-ES算法的搜索空间;结合其臂腕分离的特点,分别对手腕位置和接近矢量建立了适应度函数,降低了算法的搜索维度。 (2)利用CMA-ES算法在唯一域中进行有约束寻优;采用佳点集算法均匀分布的特点,优化了算法的初始均值点;应用同样的逆解唯一域划分方法和算法,求解了一类KUKA仿人机械臂前6个关节的8组逆解。 (3)在满足精度要求的前提下,与数值法相比,本文提出的算法平均求解时间更短:在工业机器人中,CMA-ES算法平均求解速度约为5.1 ms/次,数值法平均求解速度约为7.5 ms/次;在KUKA机器人中,CMA-ES算法平均求解速度约为18.9 ms/次,数值法平均求解速度约为54.8 ms/次。CMA-ES算法在两款机器人中逆解的位置精度均能稳定在10-6mm数量级。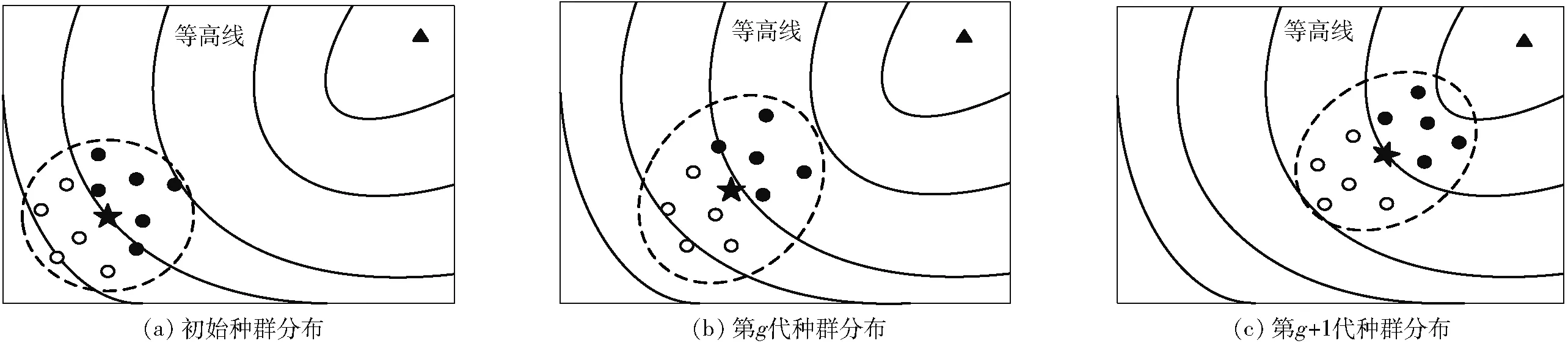
2.2 初始均值确定
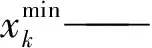
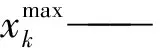
2.3 逆解处理
3 仿真算例
3.1 算例1
3.2 算例2



3.3 结果分析
4 结论

