环形沟槽几何参数对隔振区域影响的试验研究

刘晶磊， 于川情， 刘 杰

(1.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000；2.河北建筑工程学院 土木工程学院，河北 张家口 075000)

近年来，随着我国城镇化建设的深入发展，施工建设、机械运行、交通设施等产生的人工振动，对附近居民的工作和生活及精密仪器和设备的正常使用产生了不利影响，严重时甚至危及附近建筑及古建筑的安全使用和维护。目前，设置隔振屏障是解决这一环境振动问题的方法之一。隔振屏障有连续和非连续两种，对于地质较好的土层可以选择连续隔振屏障。

沟槽是一种连续隔振屏障，关于沟槽隔振国内外许多专家与学者进行大量研究。Woods[1]对沟槽进行大量试验，研究沟槽几何参数与波长比值对隔振效果的影响；Ahmad等[2]、Klevin等[3]、刘晶磊等[4]同样也进行了一系列试验研究沟槽几何参数与位置对隔振效果的影响，为设计沟槽提供了一些合理化建议；姚锦宝等[5]通过沟槽外侧任一点土体振动响应的计算公式，研究沟槽对车致振动的影响，结果表明沟槽的隔振效果与波长有关，深度对隔振效果影响相对明显，沟槽对高频振动的隔振效果较低频更为显著；徐平[6]运用波动函数展开法研究沟槽对P波、S波的隔离效果，结果表明沟槽长度对隔振效果影响较大，当沟槽长度达到6 m时，振动屏蔽区内的隔振效果超过70%；巴振宁等[7-8]采用2.5维间接边界元法建立含沟槽层状饱和地基轨道耦合动力系统，研究了沟槽对车致振动的隔振问题并分析影响因素；高广运等[9]、时刚等[10]采用薄层法，熊浩等[11]采用格子法研究了不同地基中沟槽隔振效果及其影响因素；邓亚虹等[12]采用有限元及积分隐式的方法，研究了沟槽的深度、宽度及位置对列车引起地基土体振动隔振效果的影响；淳庆等[13]采用有限元结合现场测试的方法分析了沟槽不同距离、深度及宽度对沟槽隔振效果的影响，结果表明沟槽深度对隔振效果影响较大，而宽度对隔振效果基本不影响。刘晶磊等[14]、陈昆等[15]、肖世伟等[16]通过数值分析的方法，研究了沟槽对高速铁路的隔振效果，并分析沟槽几何尺寸对隔振效果的影响。

以上研究成果中多数以矩形沟槽的隔振效果为研究对象，研究内容多停留在隔振效果及其影响因素的分析上，缺乏对沟槽隔振影响区域的分析。针对上述问题，本文以环形沟槽作为隔振屏障，采用试验的方法对环形沟槽隔振效果的影响区域进行研究，分析了深度、宽度、振源距离及沟槽圆心角因素对隔振区域分布规律的影响，并将这种影响与上述因素建立关系，为环形沟槽的设计提供了建议。

1 试验概况

开展试验的场地尺寸为4 m×4 m×2 m(长×宽×深)。将原位土换填为均质砂性土，并分层夯实，使其密度控制在1.70～1.80 g/m3,含水率控制在12%～13%。试验采用WS-Z30型振动台控制系统，其中包括信号发生器、激振器、电荷放大器、功率放大器、加速度传感器(灵敏度为4 PC/m/s2，频率响应为0.20～8 000 Hz，测量范围为50 m/s2，质量为28.50 g)，数据采集控制仪、加速度计放大器等，部分试验设备如图1所示。本试验选定的激振频率[17]为30 Hz、60 Hz、120 Hz，激振波为正弦波，采样频率设置为5 000 Hz，时间为3 s。同时，在整个试验过程中，电荷放大器值始终保持一致。

图1 现场试验及设备Fig.1 Test site and equipment

试验场地布置情况如图2所示，其中,AB为平行于试验场地中线的直线。激振器布置在AB直线一侧土体表面之上，主要作用是充当振源。环形沟槽围绕激振器布置且关于AB对称，其半径设置为100 cm。本试验中，由于隔振区域关于AB对称，因此测试区域取环形沟槽的一半作为研究对象。为准确测试瑞利波经过环形沟槽前后的变化情况，本试验根据环形沟槽圆心角设置不同个数的编组，每个编组以振源为圆心且相邻编组的夹角布设为10°，具体编组工况，见表1。

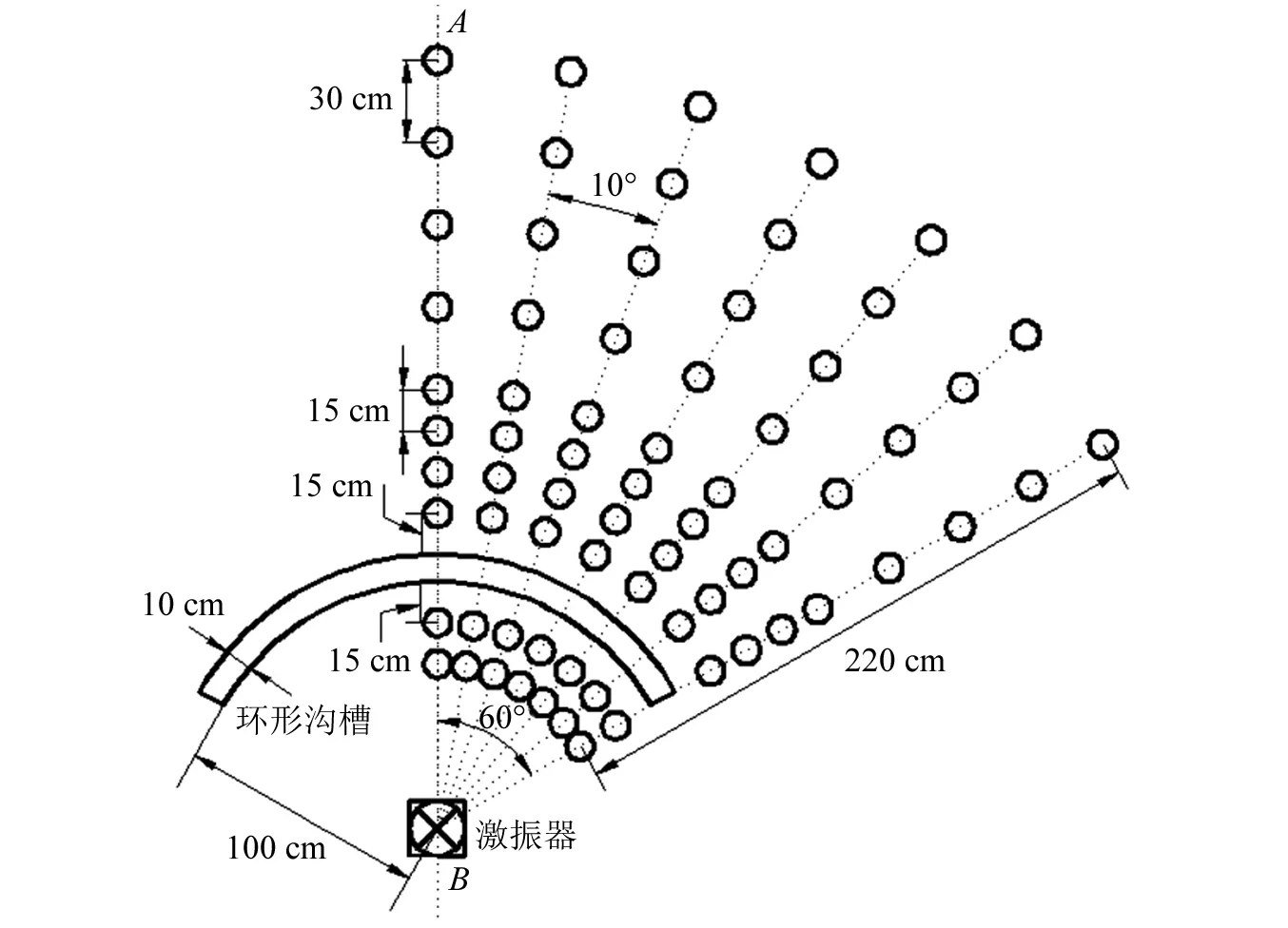
图2 试验场地布置图Fig.2 The layout of the test site

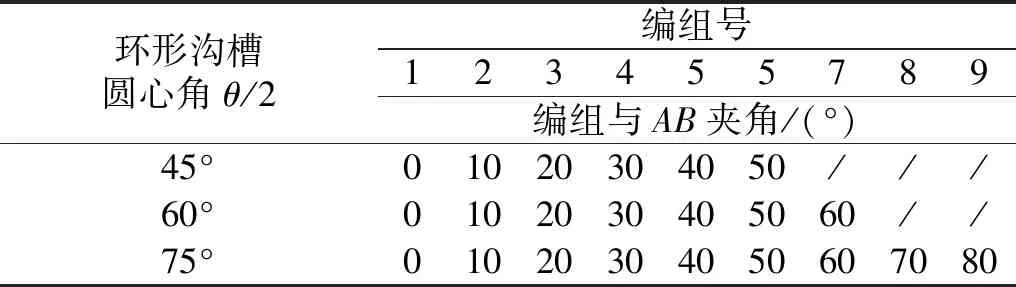
环形沟槽圆心角θ/2编组号123455789编组与AB夹角/(°)45°01020304050///60°0102030405060//75°01020304050607080

每个编组均采用10个加速度传感器，各传感器与振源的相对位置，见图2。所涉及1#、2#传感器布设于环形沟槽内侧(即激振器一侧)，3#～10#传感器局布设于沟槽外侧，2#和3#两传感器与环形沟槽边界间距固定为15 cm。环形沟槽参数水平如表2所示。

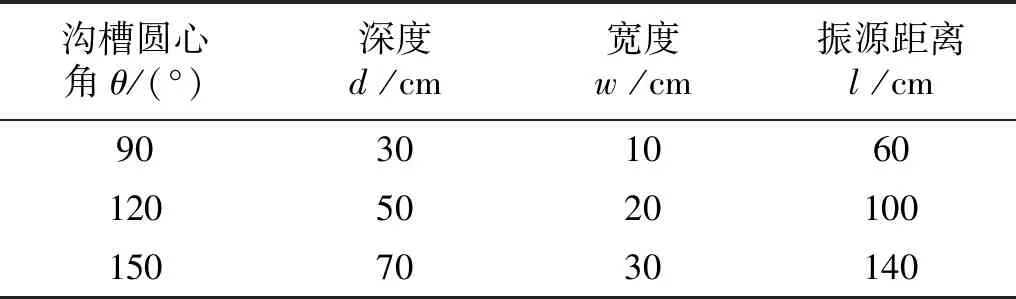
表2 环形沟槽参数水平Tab.2 The parameter level of annular trench

2 评价指标

2.1 隔振效果评价指标

每种试验工况均重复三次并选择较平缓的时域曲线的加速幅值的平均值作为该点的竖向加速度。本试验采用地表振幅降低比Ar作为评价指标，其目的是衡量隔振效果，Ar表达式见式(1)，Ar越小表示隔振效果越好

Ar=a1/a0

(1)

式中：a1为设置环形沟槽时测点的加速度值；a0为无环形沟槽时对应测点的加速度值。

2.2 参数分析指标

为了研究环形沟槽的尺寸及振源距离对隔振区域的影响，引入下列参数对其进行分析评价。

(1) 深度参数D

环形沟槽深度d与瑞利波波长λR的比值为D，表示环形沟槽深浅对其隔振区域影响的物理量。计算式为

D=d/λR

(2)

式中：d为环形沟槽的深度；λR为瑞利波波长。

(2) 宽度参数W

环形沟槽宽度w与瑞利波波长λR的比值为W，表示环形沟槽宽度对其隔振区域影响的物理量。计算式为

W=w/λR

(3)

式中：w为环形沟槽的宽度；λR为瑞利波波长。

(3) 距离参数L

环形沟槽振源距离l与瑞利波波长λR的比值为L，表示环形沟槽位置对其隔振区域影响的物理量。计算式为

L=l/λR

(4)

式中：l为环形沟槽与振源距离；λR为瑞利波波长。

3 瑞利波波速测定

试验采用表面波频谱分析方法[18]测定瑞利波波速。在试验场地上布置1#和2#传感器，在激振荷载作用下，瑞利波从振源首先经过1#传感器传向2#传感器并向外继续传播。利用频谱分析方法，可得到两信号的互功率谱和相干函数频谱图。在互功率谱中可得到波在传播过程中时间滞后所产生的相位差；利用相干函数可以评价频段上信号的质量。相干函数在某频段上接近于1，表示信号1和信号2在该频段上具有良好的相关性，试验中若相干函数值大于0.85[19]则可视为相干性良好，即为1#～2#传感器接收到的为同一波。图3给出了现场瑞利波波速测定传感器布置图。

图3 波速测定传感器布置图Fig.3 The layout of sensor for the measurement ofwave velocity

瑞利波从1#传感器到2#传感器所需要用的时间t可根据相位差算得，计算式为

t=φ/(360f)

(5)

式中：t为时间；φ为相位差；f为频率。

两传感器的距离X是已知的，波依次通过1#和2#传感器，因此瑞利波波速的计算式为

VR=(360Xf)/φ

(6)

式中：VR为瑞利波波速；X为两传感器距离。

依据波速、频率和振动波长存在式(7)关系，可得出不同频率下瑞利波的波长。

λR=VR/f

(7)

式中：λR为瑞利波波长；VR为瑞利波波速；f为频率。

将试验结果代入式(5)与(6)可得到瑞利波波速，瑞利波波速取均值为109.99 m/s；将瑞利波速代入式(7)可计算出瑞利波波长，经计算瑞利波波长最大值为3.67 m，最小值为0.92 m。

4 隔振区域试验结果分析

4.1 深度对隔振区域的影响

为了研究环形沟槽深度对隔振区域的影响，试验采用宽度为20 cm、圆心角为120°、振源距离为100 cm的环形沟槽作为研究对象，将深度作为变量。激振频率采用30 Hz(低频)、60 Hz(中频)、120 Hz(高频)作为对比工况，具体工况见表3。

表3 参数d试验安排Tab.3 The test arrangement of parameter d

徐平等[20]以隔振效果40%为例，分析矩形沟槽几何参数对隔振区域的影响，基于此，本试验以环形沟槽外侧且Ar值处于0～0.35的区域(即隔振效果达到65%的区域)作为有效隔振区域，用来分析环形沟槽对有效隔振区域分布规律的影响。

综合考察低中高频不同工况，这里以中频60 Hz为例说明问题，其它试验工况Ar值的等值线图作为校核对比，未在文中给出。选取表3中的工况1-4～1-6进行深度隔振效果分析，振幅降低比的二维等值线图如图4所示。环形沟槽设置于数据采集区AB线上距激振器100 cm处，传感器设置与图2对应。图4中标注的S1和S2为两条以激振器为圆心的弧线，供分析之用，下文中不再重复说明。

对比工况1-4～1-6，数据采集区内Ar的等值线产生了一些相同变化，体现在如下三方面：首先，在隔振区域内与AB轴线形成了一个扇形的有效隔振区域，有效隔振区域内Ar值处于0～0.35，环形沟槽显示出了一定的隔振效果。同时，D值从0.16增大到0.38时，有效隔振区域面积也在逐渐增大，S2所在位置有效隔振区域的角度增大了13°，这说明：通过增加深度，可以增大有效隔振区域面积；其次，S1和S2所在位置为两条振动加强带，随着深度的增加，两条振动加强带面积均在减小；最后，环形沟槽内侧及沟槽末端附近存在明显振动加强区，上述区域内土体振动强于周围区域。分析振动加强区域出现的原因，是由于表面瑞利波的传播途径被沟槽阻碍，瑞利波沿沟槽绕射并在隔振区域汇集而形成。

图4 工况1-4～1-6等值线图Fig.4 Amplitude reduction ratio contour map onconditions of 4～6

作进一步分析，为了分析深度变化对有效隔振区域面积的影响。本文引入了面积比η用来描述有效隔振区域面积相对变化情况，定义式为

η=A0.35/A

(8)

式中：A0.35为有效隔振区域的面积(即沟槽外侧隔振区域内Ar值处于0～0.35的区域)；A为沟槽外侧隔振区域的面积。

因此，有效隔振区域面积先求得，如表4所示。绘制回归方程的拟合图像，如图5所示。由图5可知，随着D值不断增大，η值也在不断增大：当D值小于0.31时，η值增大了0.18，此时，增加环形沟槽深度，可以显著增大有效隔振区域的面积；当D值为0.31～0.54时，η值增大了0.08，此时，有效隔振区域面积继续增大，但增加幅度相对减小；当D值为0.54～0.77时，η值增大了0.05，此时，有效隔振区域变化不明显。对采集到的数据进行整理，并对数据进行拟合，在不同工况下，D与η相关关系如式(9)所示

表4 隔振区域面积一览表Tab.4 List of vibration isolation area

η=0.14lnD+0.72,R2=0.85

(9)

综上分析可知，环形沟槽深度是影响有效隔振区域分布的重要参数。在一定范围内，通过增加深度可以显著增大有效隔振区域面积，限于本文试验条件，当D值为0.54～0.77时，有效隔振区域面积变化不明显。

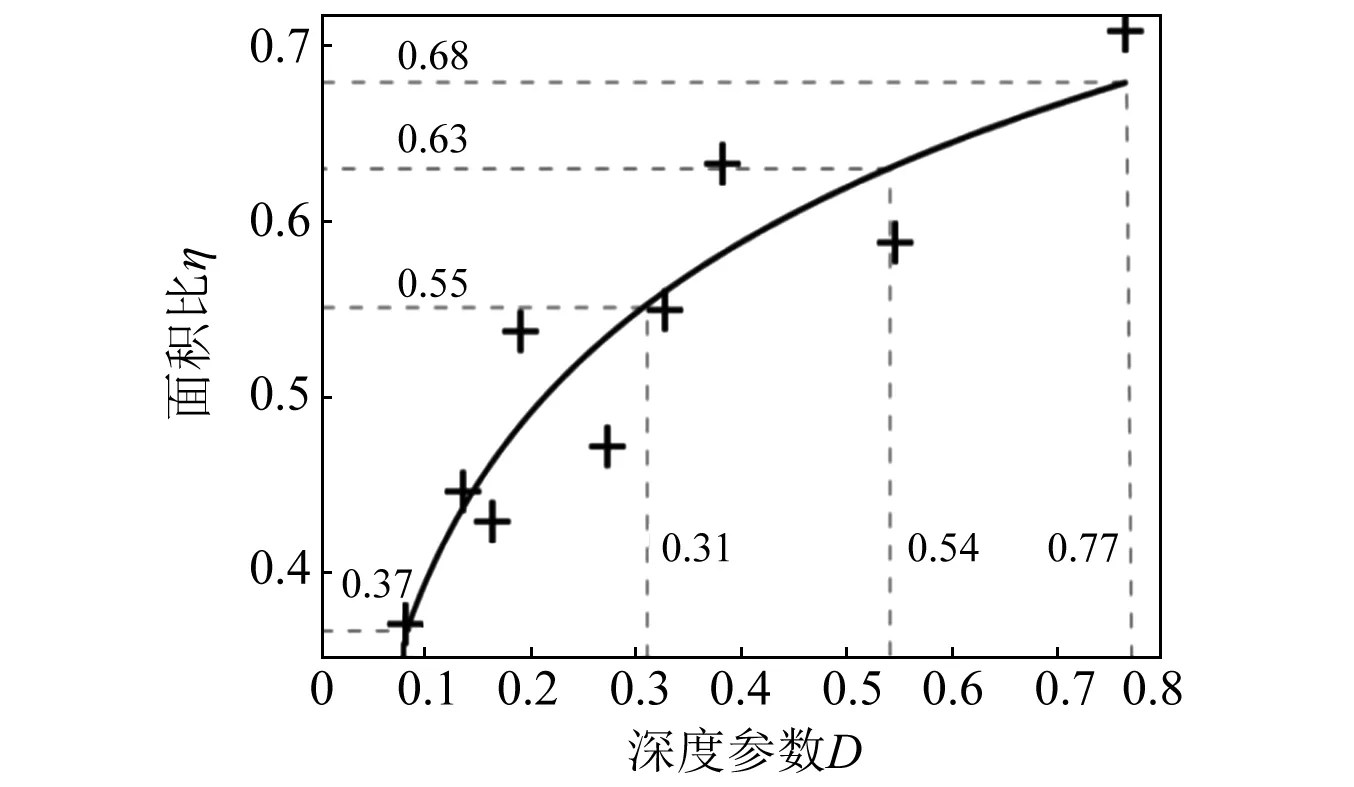
图5 D与η拟合曲线Fig.5 The fitting curve of D and η

4.2 宽度对隔振区域的影响

为了研究环形沟槽宽度对隔振区域的影响，试验采用深度为50 cm、角度为120°、振源距离为100 cm的环形沟槽作为研究对象，将宽度作为变量。同深度试验安排相同，激振频率同样采用30 Hz(低频)、60 Hz(中频)、120 Hz(高频)作为对比工况，具体工况如表5所示。

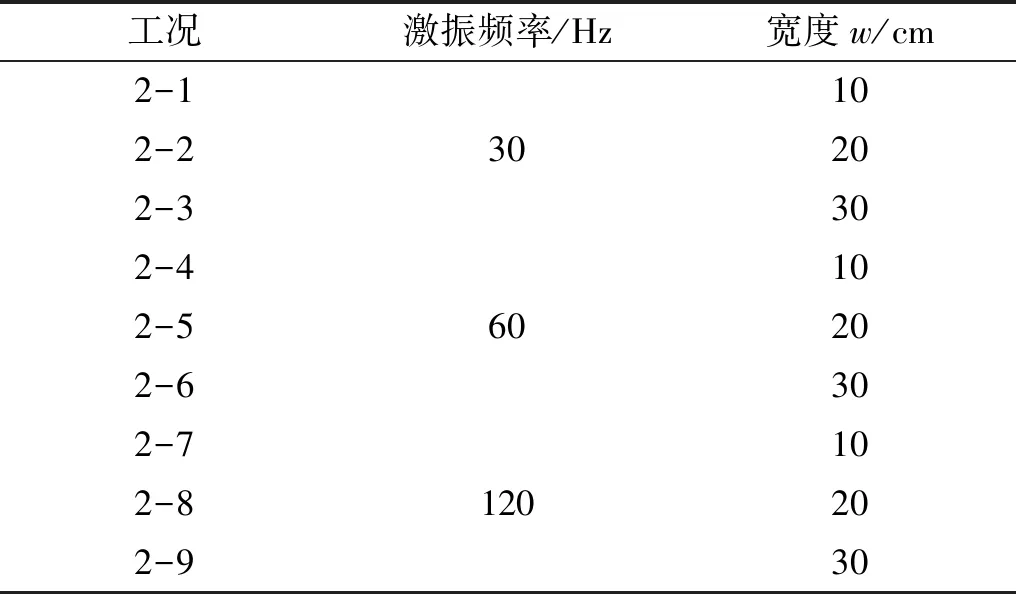
表5 参数w试验安排Tab.3 The test arrangement of parameter w

综合考察各工况并同深度试验分析一致，这里以中频60 Hz为例说明问题，其它试验工况Ar值的等值线图作为校核对比，未在文中给出。以表5中工况2-4～2-6为例进行宽度隔振效果分析，Ar的二维等值线图如图6所示。其中，工况2-5的等值线图参见图4工况1-5所示。

对于工况2-4～2-6而言，沟宽变化对Ar的二维等值线图产生了两方面相同的影响。首先是隔振效果：沟后形成一定范围的有效隔振区域，并且随着沟槽宽度的增大，有效隔振区域的面积也逐渐增大。其次是振动加强区域：与研究深度对隔振区域影响相同，振动加强区位于沟槽内侧及沟槽末端并延伸至沟槽末端隔振区域内，产生的原因主要是由于瑞利波的绕射。振动加强区域在下文试验中均不同程度存在且与深度试验分布规律基本相同，下文中不再重复说明。相比于深度参数对隔振区域的影响，宽度参数对隔振区域的影响表现出了异同点。第一，如工况2-4所示在隔振区域S2所在位置，出现一条角度为60°振动加强带，Ar值处于0.35～0.70之间。产生的原因是由于瑞利波穿过沟槽底部而形成的。第二，当深度一定时，可以增加沟槽宽度，从而增大有效隔振区域的面积，如工况1-5和2-6所示。这是因为增加沟槽宽度，可以减少沟底瑞利波绕射。

图6 工况2-4、2-6等值线图Fig.6 Amplitude reduction ratio contour map onconditions of 4、6

同深度分析方法相同，利用面积比η分析沟槽宽度对有效隔振区域面积的影响。有效隔振区域面积如表6所示。对采集到的数据进行整理，并对数据进行拟合，绘制回归方程的拟合图像，如图7所示。

表6 隔振区域面积一览表Tab.6 List of vibration isolation area

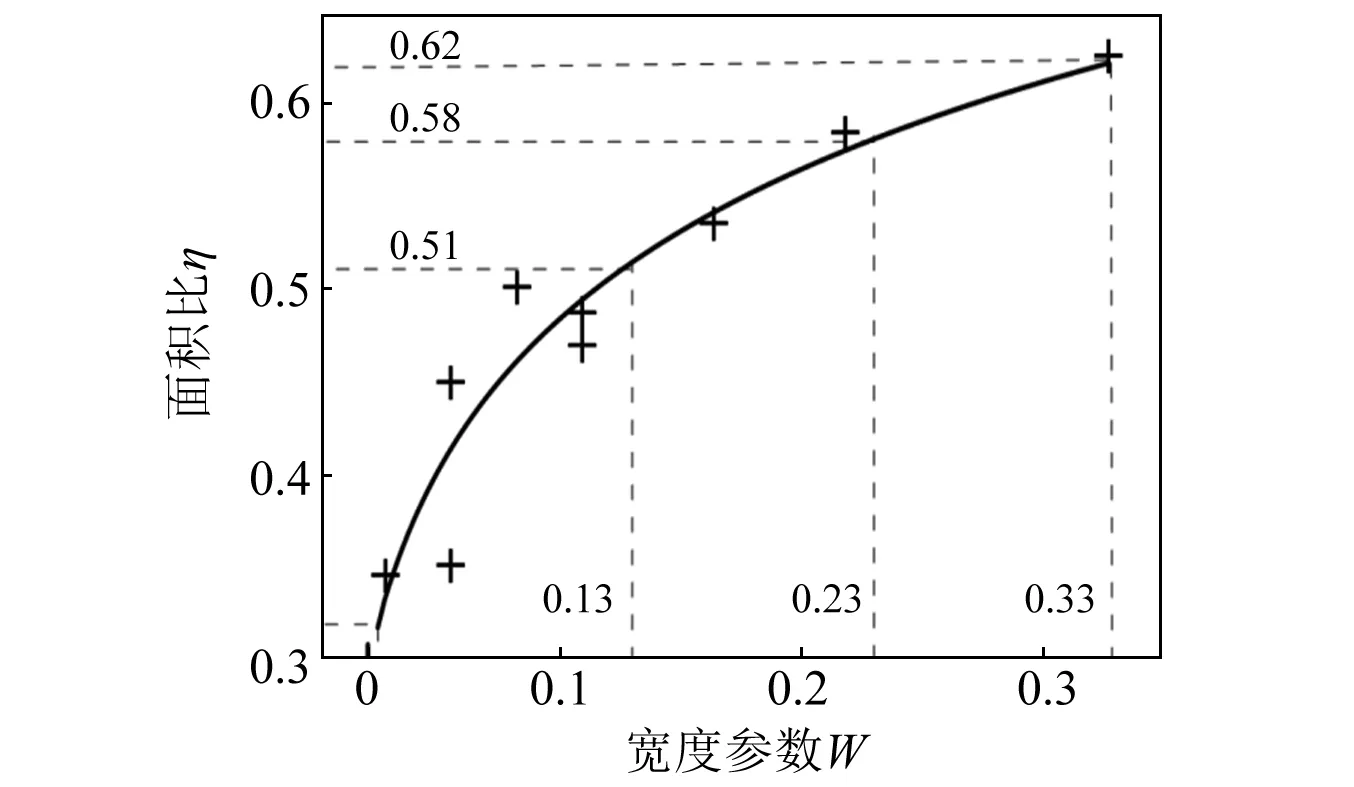
图7 W与η拟合曲线Fig.7 The fitting curve of W and η

由图7可知，随着W值不断增大，η值也在不断增大：当W小于0.13时，η值增大了0.19，此时，增加沟槽宽度可以显著增大有效隔振区域面积；当W取0.13～0.23时，η值增大了0.07，此时，沟槽的有效隔振区域面积继续增大，但增加幅度相比较小；当W取0.23～0.33时，η值增大了0.04，此时，有效隔振区域面积虽然不断增大，但效果不明显。在不同工况下，W与η相关关系式为

η=0.81W0.25，R2=0.89

(10)

综上分析可知，环形沟槽宽度对有效隔振区域分布影响较大。限于本文试验条件，W取0.23～0.33时，可以获得良好有效隔振区域面积。

4.3 振源距离对隔振区域的影响

为了研究振源距离对隔振区域的影响，试验采用深度为50 cm、宽度为20 cm、角度为120°的环形沟槽作为研究对象，将振源距离作为变量。同深度试验安排相同，激振频率同样采用30 Hz(低频)、60 Hz(中频)、120 Hz(高频)作为对比工况，具体试验工况如表7所示。

表7 参数l试验安排Tab.7 The test arrangement of parameter l

综合考察各工况并同深度试验分析一致，这里以中频60 Hz为例说明问题，其它试验工况Ar值的等值线图作为校核对比，未在文中给出。

以表7中的工况3-4～3-6为例进行振源距离隔振效果分析，Ar的二维等值线图如图8所示。其中，工况3-5的等值线图参见图4工况1-5所示。对比工况3-4～3-6，振源距离的改变对Ar的二维等值线产生了两方面的影响。首先是对有效隔振区域的影响：当振源距离较小时，有效隔振区域的分布是不连续的，如图8工况3-4所示，隔振区域内形成S1和S2两条振动加强带将有效隔振区域分成3部分。随着振源距离不断增大，3部分有效隔振区域逐渐连接成一个整体，这是由于当振源距沟槽较近时，瑞利波在沟底和沟槽末端产生两方面绕射现象，随着振源距离不断增大经过沟底瑞利波的数量不断减小，沟槽末端绕射现象也在不断减弱，期间伴随瑞利波能量的消耗；其次是对有效隔振区域面积的影响：通过增大振源距离，隔振区域内的S1和S2两条振动加强带逐渐减小，与之相对应的是有效隔振区域的面积增大，图工况1-5和3-6所示。

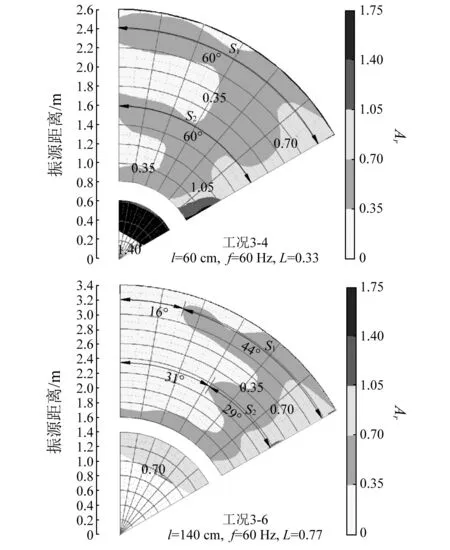
图8 工况3-4、3-6等值线图Fig.8 Amplitude reduction ratio contour map onconditions of 4、6

进一步分析，同样利用面积比η去分析振源距离对有效隔振区域面积的影响。有效隔振区域面积如表8所示。对数据进行拟合并绘制拟合图像，如图9所示。随着L增大，η值也在不断增大，这表明随着振源距离的增加，有效隔振区域面积所占整个隔振区域面积的比例随也不断增加。当L值小于0.50时，η值增大了0.18，此时，增加振源距离可以显著增大有效隔振区域面积；当L值在0.50～0.84和0.84～1.18时，η值分别增大了0.08和0.06，此时，沟槽的有效隔振区域面积继续增大，但增加的幅度相比较小；当L值在1.18～1.52时，η值增大了0.04，此时，有效隔振区域面积增加不明显。在不同工况下，L与η相关关系如式为

η=0.16lnL+0.58，R2=0.82

(11)

综上分析可知，振源距离对有效隔振区域的分布有较大影响，可以通过增加振源距离获得良好的有效隔振区域面积。限于本文试验条件，建议L取值范围为1.18～1.52。

表8 隔振区域面积一览表Tab.6 List of vibration isolation area

4.4 环形沟槽圆心角对隔振区域的影响

为了研究环形沟槽圆心角对隔振区域的影响，试验采用深度为50 cm、宽度为20 cm、振源距离为100 cm的环形隔振沟槽作为研究对象。将圆心角作为变量，激振频率同样采用30 Hz(低频)、60 Hz(中频)、120 Hz(高频)作为对比工况，具体试验工况见表9。

表9 参数θ试验安排Tab.9 The test arrangement of parameter θ

综合考察各工况并同深度试验分析一致，这里以中频60 Hz为例说明问题，其它试验工况Ar值的等值线图作为校核对比，未在文中给出。以表9中的工况4-4～4-6为例进行分析，Ar的二维等值线图如图10所示，其中，工况4-5的等值线图参见图4工况1-5所示。

对比工况4-4～4-6，环形沟槽圆心角的改变对Ar的有效隔振区域产生了三方面的影响。首先是隔振区域分布的影响：如工况4-4所示，隔振区域内形成两条角度为45°的振动加强带S1和S2，S1和S2两条振动加强带将有效隔振区域分成不连续的3部分，随着环形沟槽圆心角的增加，有效隔振区域逐渐构成一个整体；其次是对有效隔振区域面积的影响：随着环形沟槽圆心角的增加，S1和S2两条振动加强带的圆心角在不断减小，与之相对应的是有效隔振区域面积逐渐增大；产生以上两个方面的变化规律是由于瑞利波沿沟槽末端绕射引起；最后是环形沟槽圆心角对振动加强带的影响：随着环形沟槽圆心角的增大，S1和S2两条振动加强带与AB夹角也在不断增大，但通过对比工况4-4～4-6可知，S1和S2两条振动加强带的圆心角均未小于39°，产生原因主要与瑞利波在沟槽末端绕射能力有关。

进一步分析，同样利用面积比η去分析环形沟槽圆心角对有效隔振区域面积的影响，有效隔振区域面积，见表10。对采集到的数据进行整理，并对数据进行拟合，绘制回归方程的拟合图像，见图11。

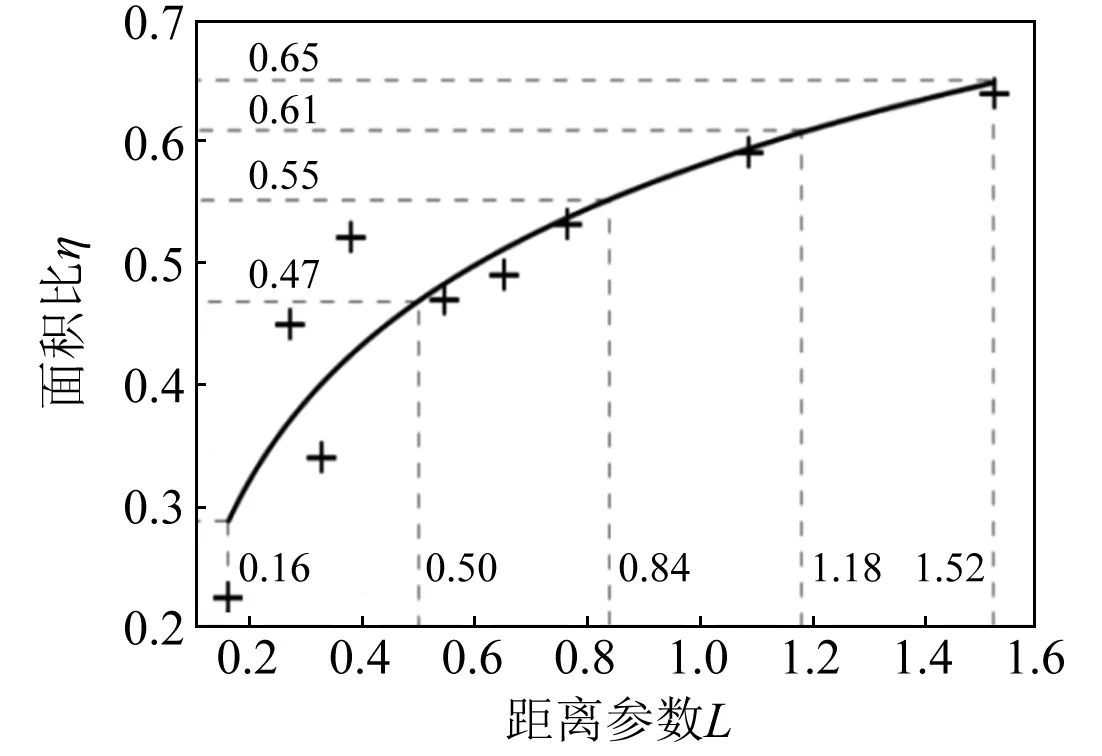
图9 L与η拟合曲线Fig.9 The fitting curve of L and η

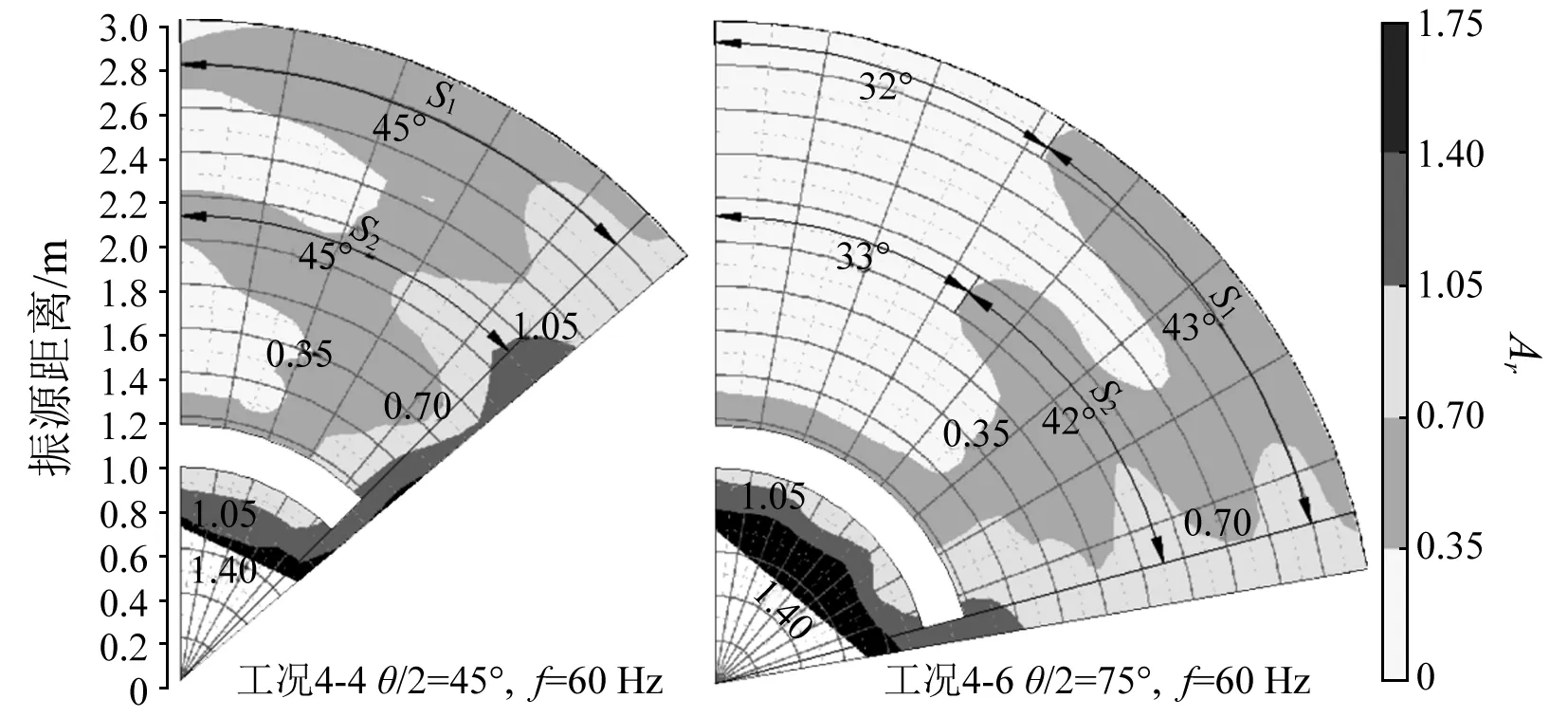
图10 工况4-4、4-6等值线图Fig.10 Amplitude reduction ratio contour map onconditions of 4、6

工况4-14-24-34-44-54-64-74-84-9A0.350.621.782.620.831.863.221.252.343.56η0.210.450.530.280.470.650.420.590.72注:A45=2.97 m2、A60=3.96 m2、A75=4.95 m2其中,45/60/75代表环形沟槽圆心角的一半,单位:度

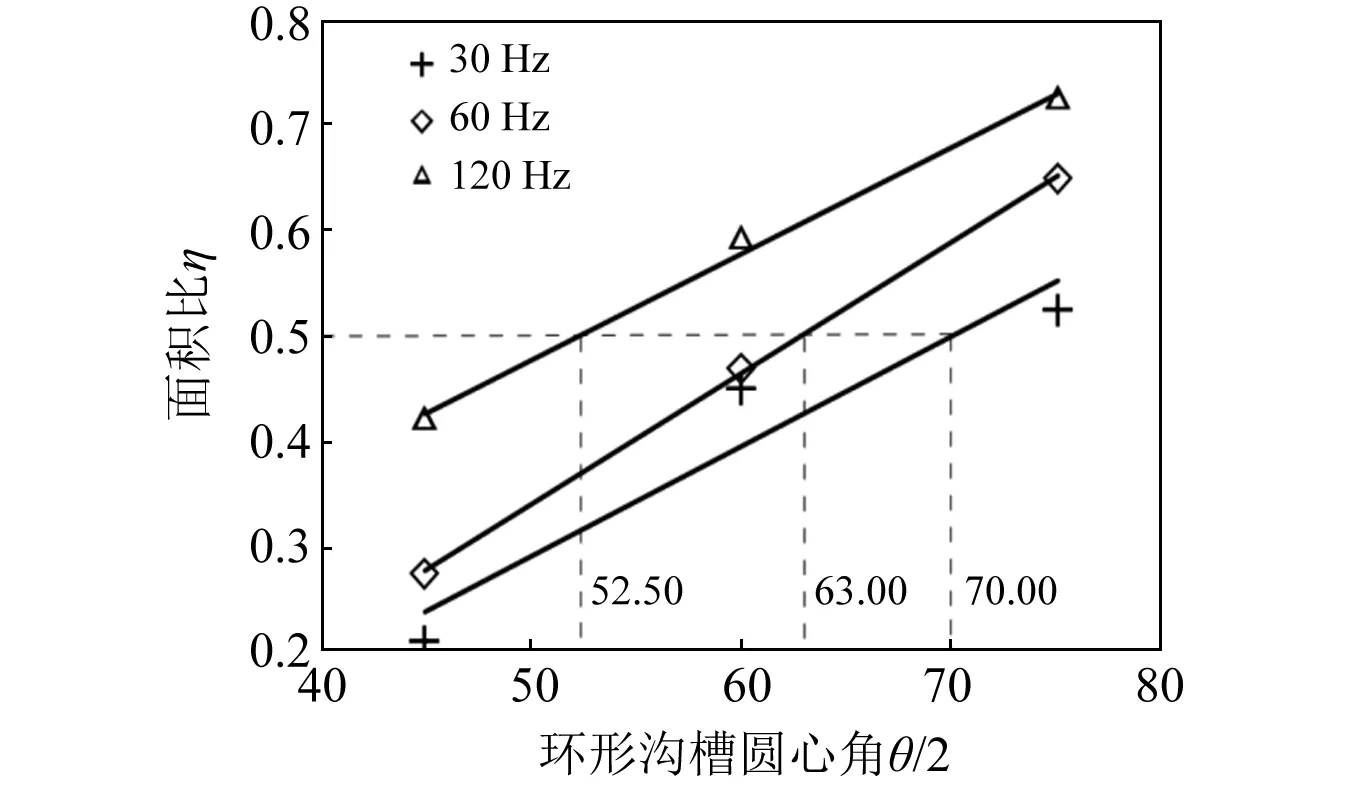
图11 θ与η拟合曲线Fig.11 The fitting curve of θ and η

图11给出了3条不同频率的θ与η拟合曲线，其中，3条拟合曲线上升趋势相同：随着θ值不断增大，η值也在不断增大，这表明增大环形沟槽圆心角可以显著提高有效隔振区域的面积。另外，频率不同，3条拟合曲线的位置也不同。随着频率的增大，拟合曲线位置依次上升，这表明当环形沟槽圆心角一定时，有效隔振区域面积随激振频率增加而增大。换而言之，当有效隔振区域面积一定时，环形沟槽圆心角随频率的减小而增大。以η=0.5为例，激振频率分别取120 Hz、60 Hz、30 Hz时，对应所需环形沟圆心角依次为105°、126°、140°。在不同工况下，θ与η相关关系，见表11。

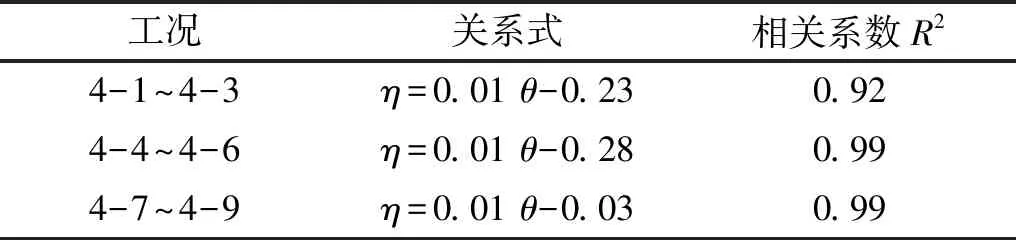
表11 θ与η的相关性分析Tab.11 The correlation analysis of θ and η

综上所述环形沟槽圆心角是影响有效隔振区域的分布的重要参数。选取环形沟槽圆心角时，宜优先选取大于90°的环形沟槽；另外，环形沟槽圆心角的选取与频率有关，达到同等有效隔振区域面积，频率越小所需圆心角越大。

5 结 论

本文通过室外试验的方法，绘制试验场地振幅降低比的二维等值线图，以Ar≤0.35的区域(有效隔振区域)作为研究对象，对影响该区域分布的几何因素进行了研究，主要结论如下：

(1)环形沟槽的深度、宽度、振源距离及其圆心角均会对有效隔振区域产生影响。设计环形沟槽时，应将上述几何参数综合考虑。

(2) 深度对有效隔振区域的影响：隔振区域内形成较为完整的有效隔振区域，随着深度的增加，有效隔振区域面积不断增大。限于本文试验条件，建议D值的取值范围为0.54～0.77，继续增大D值，有效隔振区域面积变化不明显。

(3) 宽度对有效隔振区域的影响：起初有效隔振区域被分割成不连续的两部分，随着宽度的增加，有效隔振区域连接为一个整体并不断得到加强。在沟槽深度相同时，可以通过增加宽度进而加强有效隔振区域面积，建议W取值范围为0.23～0.33。

(4) 振源距离与环形沟槽圆心角对隔振区域的影响较为相似。变化规律为随着参数的增加，有效隔振区域被分割为不连续的三部分，随后有效隔振区域连接为一个整体并不断得到加强。建议L取值范围为1.18～1.52。

(5) 环形沟槽圆心角的选取与频率有关。达到同等有效隔振区域面积，频率越小所需圆心角越大。宜优先选取大于90°的环形沟槽，否则隔振区域内将形成不连续的有效隔振区域。