伺服阀用超磁致伸缩致动器结构设计及输出位移建模

郑佳伟， 何忠波， 周景涛， 薛光明， 荣 策， 柏 果

(陆军工程大学 石家庄校区 车辆与电气工程系，石家庄 050003)

电液伺服阀(Electro-Hydraulic Servo Valve, EHSV)，是电液伺服控制系统的关键部件。它具有控制精度高、输出功率大、动作灵活等优点，因而在航空航天、国防军事工业等领域获得广泛应用[1-2]。阀用致动器(又称电-机转换器)作为连接电气元件和液压元件的桥梁，是EHSV乃至液压控制系统的核心元件之一，其性能的优劣，直接关系到EHSV的性能指标。现阶段用于EHSV的致动器主要包括伺服电机、力矩马达及音圈电机等[3-5]，但传统的致动器往往不能兼具高频响、高输出等特性，因此在一定程度上限制了EHSV在某些动态性能要求较高的场合上的应用。

目前，将新型功能材料应用于高性能致动器的研究逐渐成为热点[6-11]，其中以超磁致伸缩材料(Giant Magnetostrictive Material，GMM)为基础的超磁致伸缩致动器(Giant Magnetostrictive Actuator，GMA)因具有精度高、能量大、响应快、结构简单等优点而备受青睐[12-16]。对于不同的使用用途，所设计GMA结构不同，Sato等[17]设计了一种GMM棒串联布置的GMA，在GMA中，6根GMM棒被分成2组，分别置于“Z”型夹持器两端，可实现2组棒输出位移的叠加，且GMA上端安装有位置传感器，用于监测输出位移并进行反馈；范文涛等[18]设计了圆筒状GMA，并通过建模与仿真的方法研究了GMM筒轴向长度对磁场强度及均匀性的影响；薛光明等[19]设计了用于驱动高压共轨喷油器球阀的GMA，并建立了将轴向磁场不均匀性考虑在内的多自由度动力学模型；崔旭等[20]设计了带有套筒结构的阀用GMA，通过GMM棒料、GMM筒料与套筒间配合，能在几乎不损失机械性能的前提下有效减小GMA的总体积。

不同学者为解决特定问题以满足GMA的驱动要求，设计了不同结构的GMA。本文在上述基础上，针对传统永磁偏置式GMA轴向磁场均匀性差的问题，设计了一种具有分布式永磁偏置结构的阀用GMA，通过仿真分析的方法确定了GMM棒与永磁体的最佳分布结构，并以此阀用GMA为研究对象，建立了其输出位移模型，制作了GMA样机，进行了相关实验。

1 阀用GMA偏置磁场结构设计

1.1 阀用GMA的工作原理

阀用GMA装置结构如图1所示，其主要由GMM棒、永磁体、驱动线圈、输出杆及预压弹簧等组成。工作时，驱动线圈在通入电流的作用下产生驱动磁场，该磁场与偏置磁场共同作用于GMM棒，使其发生磁致伸缩应变，同时，产生轴线方向的微位移，该位移经输出杆传递，进而驱动阀芯工作。预压碟簧通过前、后端盖之间间距的调节，为GMM棒提供合适的预压力。冷却腔内通入流动的冷却液，可使整个GMA工作于相对稳定的环境温度中。

1. 外壳 2. 左端盖 3. 驱动线圈 4. 冷却腔 5. 线圈骨架 6. 右端盖 7. 碟簧 8. 输出杆 9. 冷却液入口 10. GMM棒 11. 冷却液出口 12. 永磁体 图1 阀用GMA结构图Fig.1 Structure diagram of GMA

1.2 阀用GMA偏置磁场结构仿真设计

阀用GMA体积大小往往受工作环境限制，因此设计永磁偏置结构时，采取控制变量的方法，在限定永磁体及GMM棒总长度及半径不变的基础上，研究永磁体和GMM棒段数对GMM棒内偏置磁场强度影响。设定GMM棒总长度为L=45.0 mm，共n段，永磁体总长度为l=15.0 mm，共n+1段，二者半径均为r=4.0 mm，即可得各段GMM棒、永磁体长度Ln、ln分别为：

(1)

有限元建模时，忽略GMA中预压碟簧、进出液口等特征部件，同时利用软件中二维轴对称模式对GMA模型进行简化。GMA模型各部件材料及其相对磁导率μr数值，如表1所示。

表1 部件材料及其相对磁导率Tab.1 Component material and magnetic permeability

针对阀用GMA结构特点，采用自适应网格划分方式，网格尺寸为极细化，网格划分结果，如图2所示。

设定永磁体剩磁Br=1.2 T，依次改变n值，对模型进行有限元分析，得到模型对应的偏置磁场强度分布状态，如图3所示。

图3 磁场强度分布云图Fig.3 Magnetic field intensity distribution

在对各n值对应模型GMM棒轴线上偏置磁场强度进行分析时，引入磁场不均匀度指标η进行描述，η可表示为

(2)

式中：N为等间距获取的采样点个数，Hi为第i个采样点的磁场强度，Havg为所取采样点的平均磁场强度。

磁场不均匀度η越小，则GMM棒内的磁场均匀性越高，对应GMA的输出效果(包括输出位移及输出力)越好，进而使得其所驱动的阀芯具有更好的动态性能。

经对采集数据进行处理后，得到η、Havg数值随GMM棒段数n增加的变化，如图4所示。

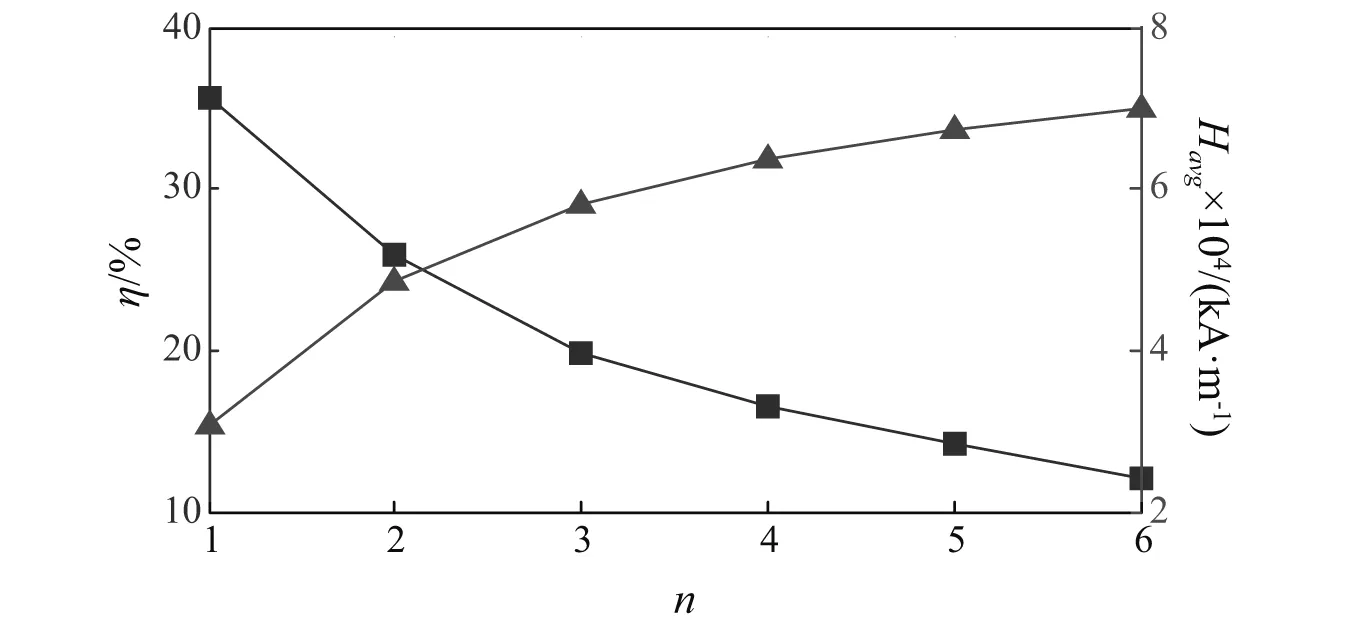
图4 n值对偏置磁场的影响Fig.4 Influence of n on bias magnetic field

由图4可知，随着GMM棒段数的增加，其轴线方向上的平均磁场强度逐渐增大，磁场分布不均匀度也在逐渐降低，由此可知，采用分布结构的偏磁施加方式是合理的。同时，考虑到GMM脆性较大，切割加工较难，且过薄的永磁片在反向磁场中易退磁等原因，最终确定偏磁施加的最佳分布结构为GMM棒数n=3时，此时GMM棒轴线上偏置磁场强度Hb随其轴线距离xr变化趋势，如图5所示。

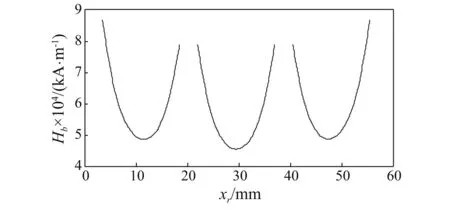
图5 磁场强度分布图Fig.5 Magnetic field intensity distribution

2 阀用GMA输出位移建模及求解

2.1 阀用GMA输出位移建模

阀用GMA输出位移建模包括建立电流-磁场强度-磁化强度-磁致伸缩应变-位移的模型。

作用于GMM棒内的磁场由驱动线圈和永磁体共同提供。由于整个GMA结构具有对称性，因而其内部磁路也具有对称性。为便于分析，将致动器内部磁路沿GMM棒轴线方向剖开，即可得两条无分支磁路，其中单支磁路图如图6所示。通入电流后，驱动线圈与永磁体产生磁场，磁感线经GMM棒→永磁体→输出杆→前端盖→外壳→后端盖→GMM棒(或逆向)，形成闭合磁路。

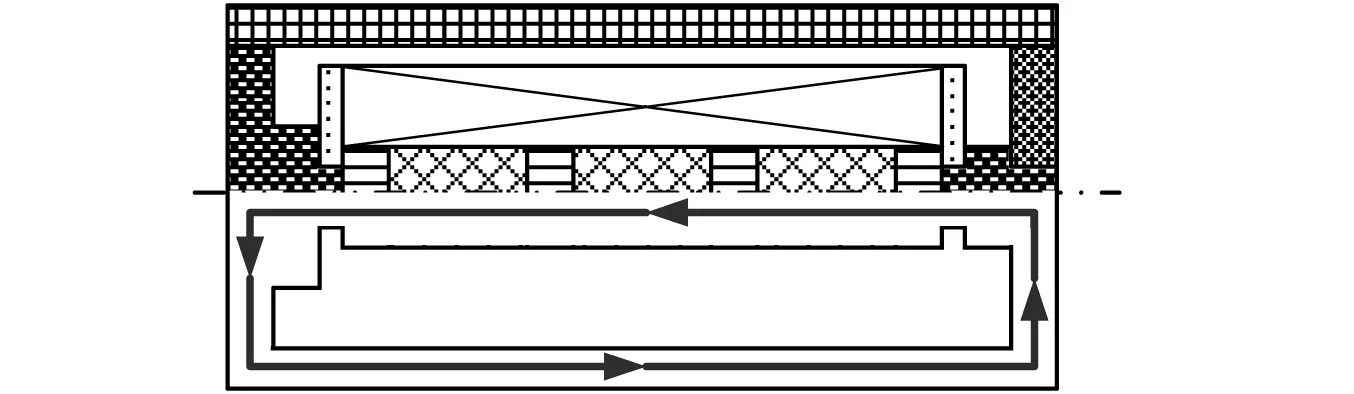
图6 单支磁路简图Fig.6 Single diagram of magnetic circuit

考虑到GMA的输出杆、外壳及前、后端盖部件均由轭铁加工，其磁阻远小于GMM棒和永磁体，可忽略不计，同时忽略空气间隙对GMA磁路的影响，从而由基尔霍夫第二定律可知，对于磁路中的任意截面，驱动磁场对应的磁通量Φ可表示为：

(3)

式中：N为驱动线圈匝数，I为驱动电流大小，Rg，μg， 分别为GMM棒的磁阻、磁导率，Rp，μp分别为永磁体的磁阻、磁导率。

穿过GMM棒截面的磁通量可由GMM棒内驱动磁场强度Hg表示为

Φ=4πr2μgHg

(4)

将式(3)代入到式(2)中，同时将GMM棒内永磁体产生的偏置磁场强度Hb进行叠加，最终可得GMM棒轴线上磁场强度H为

(5)

此处，每一段GMM棒上的偏置磁场强度取值为图5中有限元分析后对应段轴线上的平均偏置磁场强度。

磁化模型反映外界磁场强度和GMM棒磁化强度之间的关系。Jiles-Atherton模型(J-A模型)是描述这一关系的常见模型，其将材料的磁化过程解释为磁畴的转动和畴壁的移动，进而建立了一组包含明确物理含义的磁化模型方程，即

(6)

对式(6)整理可得外界磁场强度和GMM棒磁化强度之间的关系为

(7)

式中：He为GMM棒中有效磁场强度；Man为无磁滞磁化强度；Ms为饱和磁化强度；Mrev和Mirr分别为可逆和不可逆磁化强度；α为与分子场和预应力相关的磁化常数；k为钉扎系数；a为形状参数；c为可逆系数；当dH/dt>0时，δ=1； dH/dt<0时，δ=-1。δM为去除负磁化系数的参数，可以表示为

(8)

考虑到M与H的关系由非线性常微分方程给出，此处采用4阶龙格-库塔法进行求解，计算过程如下

(9)

式中：h为计算步长，Mn，Hn分别为第n步中的磁化强度和磁场强度值。

GMM的磁致伸缩应变通常用λ表示， 在一定应力作用下，对于各向同性的棒状GMM材料， 其磁致伸缩应变λ与磁化强度M的关系可用基于能量方法的二次畴转模型进行描述，即

(10)

式中：λs为饱和磁致伸缩应变系数。

根据振动理论相关知识，在对阀用GMA进行动力学分析时，考虑到GMA轴线上3段GMM棒内平均偏置磁场强度不同，将整个系统可简化为由(GMM棒+永磁体)、(GMM棒+永磁体)、(GMM棒+永磁体+输出杆)三个振动单元组成的三自由度弹簧-阻尼-质量振动系统，即如图7所示。

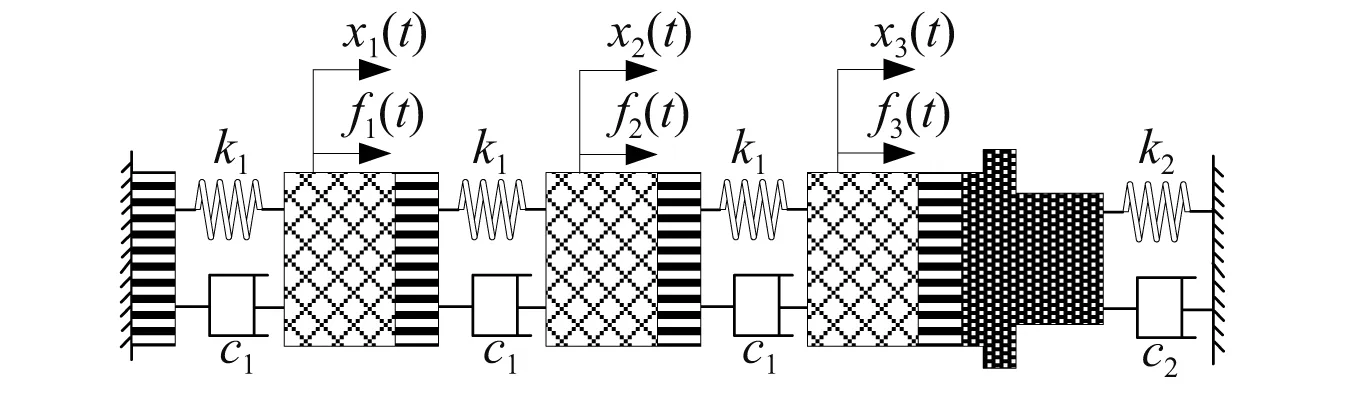
图7 振动模型图Fig.7 Diagram of vibration model

由牛顿第二定律可得振动系统的三自由度动力学模型，表示为

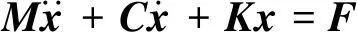
(11)

式中：M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，各振动单元位移矩阵为x=[x1(t)，x2(t)，x3(t)]T， 所承受磁致伸缩驱动力矩阵F=[f1(t)，f2(t)，f3(t)]T，mg，mp，mr分别为GMM棒、永磁体、输出杆等效质量，c1，c2分别为GMM棒和负载等效阻尼，k1，k2分别为GMM棒和负载等效刚度。

mg，mp，f与k1分别可表示为

(12)

式中：ρg为GMM棒密度，ρp为永磁体密度，g为重力加速度，Eg为GMM棒弹性模量，λ0磁致伸缩应变初值。

联立式(5)、(7)、(10)～(12)即可得阀用GMA输出位移模型。

2.2 模型求解

考虑到系统中GMM棒阻尼较大，模型解析解求取时，式(8)中矩阵方程解耦较难，精确解析解不易获取，且若对阻尼矩阵C进行对角化的简化会出现较大误差，因而采用数值方法对系统进行求解。

为便于模型的数值求解，采用状态空间法对振动模型进行描述，设振动系统的状态向量为Y=[y1，y2]T， 其中，y1，y2为

(13)

经对式(8)进行转换，振动系统的状态空间模型可表示为

(14)

式中：I为单位矩阵。

阶跃响应中，系统稳态输出位移及响应时间是判断GMA性能重要指标。此处，系统响应时间为各振动单元到达稳态时间的最大值。向系统中通入阶跃信号，系统响应至稳态后，各振动单元处的驱动磁场强度、磁致伸缩驱动力、输出位移均趋于常值。此时，系统输出可表示为

(15)

式中：x0为振动单元稳态位移矢量，F0为稳态磁致伸缩驱动力矢量，x0为GMA稳态输出位移。

谐波响应中，系统任意时刻的输出能反映出阀用GMA的在谐波激励下的响应特性。向系统中通入正弦信号，系统输出波形为类似正弦波形的拟正弦波形。系统的最终输出x3可表示为

x3=(0,0,1)(I0)Y

(16)

本文采用Matlab中lsim函数对系统阶跃响应及谐波响应进行数值求解。

3 试验测试

3.1 试验系统硬件组成

制作的阀用GMA样机如图8所示，其中，GMM棒与永磁体间采用粘接。阀用GMA样机主要参数如表2所示，其中负载等效质量、刚度、及阻尼均通过参数辨识得出。

图8 阀用GMA样机Fig.8 Prototype of GMA for valve

用于测试阀用GMA输出性能的试验系统如图9所示。其中，Rigol-DG1022U信号发生器，用于产生激励信号； GF800功率放大器，用于放大激励信号，驱动GMA工作；MicrotrakTM3-LTS-025-02激光位移传感器，精确测量位移大小；IT6932A可编程电压源，输出24 V恒定电压，为激光传感器供电；冷却机构，维持GMA工作温度基本稳定；pico-TA189电流钳，精确测量线圈电流；Rigol-DS1074Z数字示波器，采集实验数据；高斯计，用于测试GMA偏置磁场强度。

表2 阀用GMA主要参数Tab.2 Main parameters of GMA

图9 试验系统图Fig.9 Diagram of test system

3.2 偏置磁场强度分布试验

对GMM棒偏置磁场分布测试时，按从左至右的顺序，依次从各段GMM棒上(考虑到GMM棒轴线上磁场强度无法测量，因而选用棒表面沿轴向取固定一条直线测量，此处仿真分析时亦如此)等间距取5个点进行测试，共计15个测试点。每个测试点测取10组数据，取平均值，后经处理得到实验与仿真结果曲线，如图10所示。

由图可知，实验结果与仿真结果具有相同的变化趋势，说明所设计偏磁结构是合理的。

3.3 阶跃响应试验

阀用GMA的阶跃响应特性可通过其对不同幅值阶跃激励的响应曲线获取。即依次向阀用GMA中通入幅值为0.5 A，1 A，1.5 A，2 A，2.5 A，3 A，3.5 A，4 A，4.5 A，5 A的阶跃信号，待响应达到稳态后，获取阀用GMA的稳态输出位移计算结果与试验结果对比及响应时间试验结果，如图11所示。

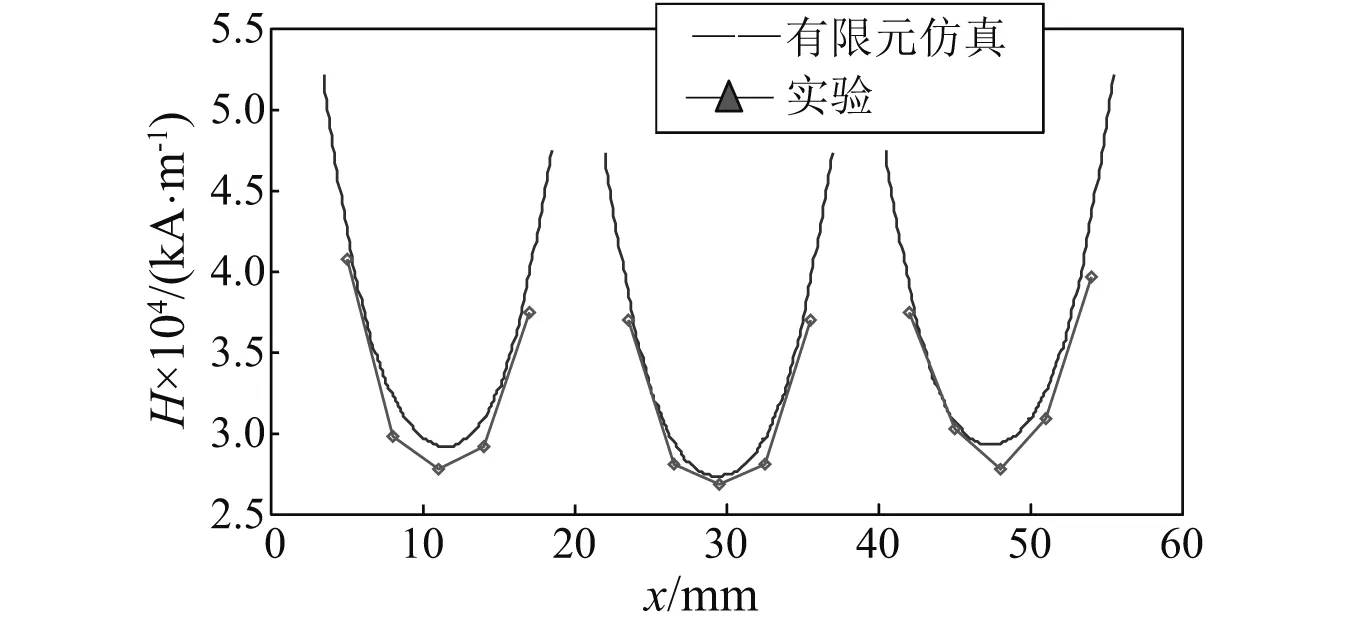
图10 实验与仿真结果图Fig.10 Experiment and simulation results

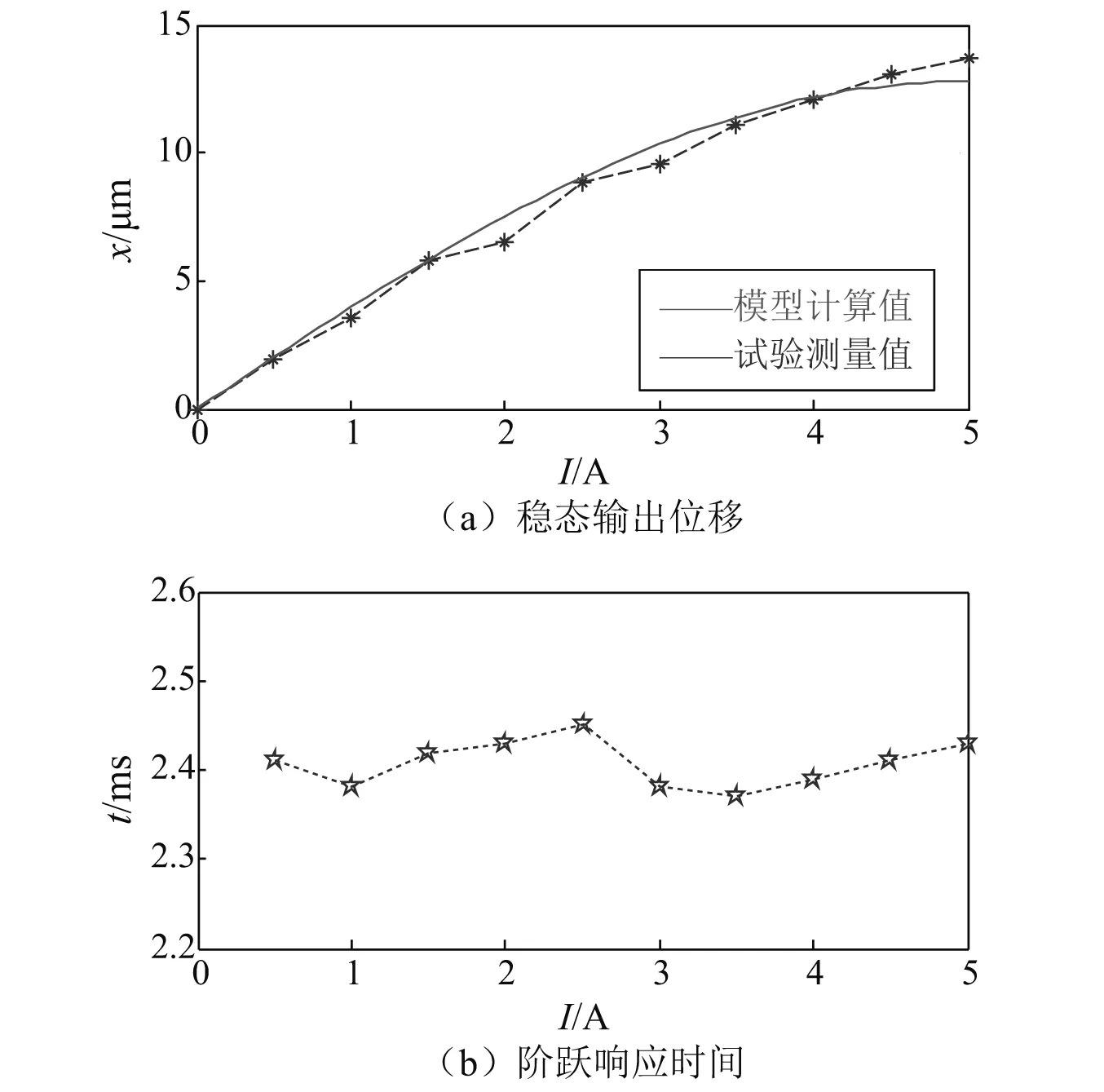
图11 阶跃响应结果Fig.11 Step response result

由数据处理结果可知，阀用GMA的稳态输出位移计算结果与试验结果基本吻合。结果对比的最大误差约为0.92 μm，相对误差为7.2%，此时通入电流值为5 A；阀用GMA的阶跃响应时间试验结果在2.37～2.45 ms间波动，说明所设计GMA能够较好满足伺服阀的驱动要求。

3.4 谐波响应试验

阀用GMA的谐波响应特性可通过其对不同频率正弦激励的响应曲线获取。即设置电流幅值为3 A，依次向阀用GMA中通入频率为20 Hz，80 Hz，160 Hz，200 Hz的正弦信号，获得阀用GMA正弦激励的响应测试结果与计算结果对比，如图12所示。

由图11可知，在20～200 Hz的频率范围内，所建阀用GMA输出位移模型的计算结果与实验结果吻合度较高。模型与实际结果之间的误差产生的原因主要有：①在实际中，GMM棒及碟簧的刚度在其工作过程中会发生改变，而模型中设为定值；②随着谐波驱动频率的增加，GMA自身的热损耗、线圈阻抗会增大，进而影响其输出特性。

图12 谐波响应结果Fig.12 Harmonic response results

4 结 论

(1) 针对传统的永磁体偏置式GMA偏置磁场强度均匀性较差的问题，设计了一种具有分布式永磁体偏置结构的阀用GMA，该GMA采用GMM棒、永磁体交替排布，能够有效提高其偏置磁场均匀度。

(2) 考虑到伺服阀工作空间环境限制，采用控制变量的方法，在限定永磁体及GMM棒总长度及半径不变的基础上，对阀用GMA偏置磁场分布结构进行了有限元仿真设计，并确定了其最佳分布结构。

(3) 基于磁阻理论、J-A模型、二次畴转模型和振动理论知识建立了阀用GMA的输出位移模型，并计算了该GMA的阶跃响应稳态输出特性及谐波响应位移-电流关系。

(4) 制作了阀用GMA样机并搭建了相关试验系统，试验结果表明：所设计阀用GMA阶跃响应时间可达2.37 ms，在20～200 Hz的频率范围内，谐波响应试验结果与模型计算结果基本吻合，验证了模型的准确性。