基于偏序集的模糊互补矩阵次序一致性检验与调整
吴 伟, 顾 丹
(1.辽宁工程技术大学 应用技术与经济管理学院,阜新转型创新发展研究院,辽宁 阜新 123000; 2.辽宁工程技术大学 党委宣传部,辽宁 阜新 123000)
0 引言
自从1977年匹茨堡大学教授萨蒂提出层次分析法(Analytic Hierarchy Process,简称AHP)以来,因其有效、实用的特点[1],该方法被广泛的应用在经济、管理、军事、技术工程等多个领域。单一准则下,人们常常通过比较两两方案的偏好信息构造判断矩阵( 通常为互反判断矩阵或模糊互补矩阵) 进行决策选择[2],相比这两种判断矩阵,模糊互补矩阵更符合人的心理习惯,更容易为决策者掌握和使用。在实际决策中,模糊互补矩阵的一致性是保证决策过程合理性的重要前提,直接影响排序向量的可靠性[2~6], 一些学者提出了包括基本一致性、满意一致性、次序一致性概念。但由于受专家的认识能力、知识水平等诸多主观因素的影响,加上客观对象本身的模糊性、复杂性,模糊互补矩阵很难保证基本一致性[7,8],魏翠萍提出当矩阵具有满意一致性时,也能得到合理的排序向量[9],文献[5]提出模糊互补矩阵满足次序一致性也能得到和专家意见一直的排序结果,并证明了满意一致性和次序一致性的等价性,杨静等人提出次序一致性是判断矩阵的基本条件[10],由不具备次序一致性矩阵获得的排序向量不可能是“对某种属性的合理测度[11~13]”,因此,为了得到准确的排序结果,有必要对判断矩阵次序一致性检验问题进行探讨。
学者们对模糊互补矩阵次序一致性检验尽管不多,但已经有了一些研究成果,文献[11]给出了检验矩阵次序一致性的通用方法;文献[8]提出用有向图讨论了判断矩阵次序一致性的性质,给出了检验判断矩阵满足次序一次性的方法;文献[5]提出判断矩阵满足次序一致性的充要条件是存在一个置换矩阵P,给出了次序一致性的标准形式和调整完全次序一致性的方法;Zhang等人通过对矩阵分解,阐述了次序一致性矩阵检验的新方法[14],侯福均提出互补判断矩阵如果任意两行对应元素大小都保持同向的关系[15],则矩阵具有可接受一致性,该方法简单、易操作,符合人们的惯性思维。另外,行和行的可比其实就是方案和方案之间可比,方案的排序是全序,具有传递性,而全序是特殊的偏序,因此蕴含了互补判断一致性问题可以用偏序集来表示。学者们对矩阵次序一致性的检验方法各有特点,都能对判断矩阵次序一致性进行有效检验,但是以上文献对矩阵次序一致性的研究也存在以下几个问题:第一,只给出检验方法,但是并未给出如何调整不一致,如文献[8]和文献[11],第二,检验和调整方法运算过程较为繁琐,判断矩阵阶数较高时,计算量较大问题,应用性较差,如文献[5]文献[11]调整过于牵强,缺乏赋值依据。基于以上分析,本文在阐述偏序集理论、模糊互补矩阵次序一致性的基础上,给出若干性质,然后讨论模糊互补矩阵次序一致性检验问题,给出hasse矩阵检验判断矩阵次序一致性的方法基础上,提出一种不满足次序一致性矩阵的调整方法。
1 基本概念
1.1 偏序集
定义1[16]设R是集合A上的一个二元关系,若R满足:
(1)自反性:对任意x∈A,有xRx;
(2)反对称性:对任意x,y∈A,若xRy且yRx,则x=y;
(3)传递性:对于任意x,y,z∈A,若xRy且yRz,则xRz。
则称R为A上的偏序关系,记作⪯,并称(A,⪯)是一个偏序集。
如果该集合对象可数,则我们可用矩阵的形式表示,称之为偏序关系矩阵[17]。
定义2[16]给定偏序集(A,⪯),对于∀ai,aj∈A,若ai⪯aj,则记sij=1;若ai≻aj或者ai与aj不可比,则记sij=0。则S=(sij)n×n为(A,⪯)的偏序关系矩阵。
由偏序关系矩阵S可以形成hasse矩阵,偏序关系矩阵转换hasse矩阵的公式:
定理1[18]设S=(sij)n×n为偏序矩阵,则HR=(S-I)-(S-I)2。
其中,S为偏序关系矩阵,HR为hasse矩阵(元素都为0和1),I为单位矩阵,矩阵(R-I)2为布尔代数。
1.2 模糊矩阵一致性
在多属性决策中,设X={x1,x2,…,xn}为方案集[19],且N={1,2,…,n}。决策者常常很难直接给出方案集的排序,但是却可以给出方案的两两优劣比较的用实数表示的模糊偏好信息bij,所给出的矩阵B=(bij)n×n,描述如下:
定义3[20]设矩阵B=(bij)n×n,若∀bij∈[0,1],则称B是模糊矩阵。
根据定义3可知:
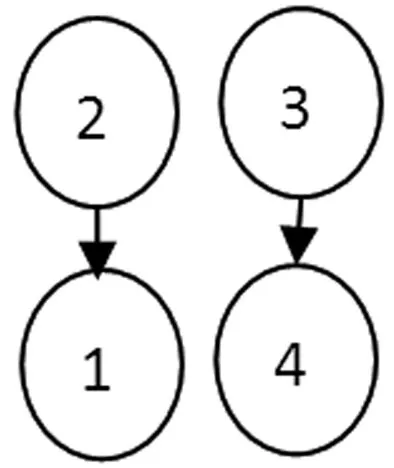
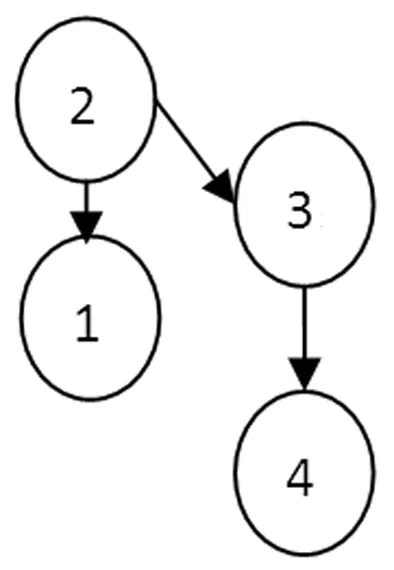
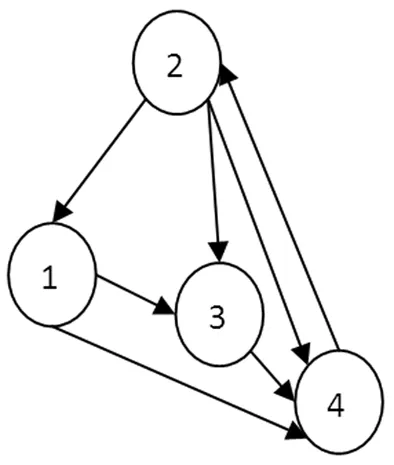
(1)0.5 (2)0≤bij<0.5,表示方案xj优于方案xi; (3)bij=0.5,表示方案xi和方案xj同样重要。 定义4[21]若模糊矩阵B=(bij)n×n满足:对于∀i,j∈N有bij+bji=1,则称B是模糊互补矩阵。 定义5[22]对模糊互补矩阵B=(bij)n×n,若对∀i,j,k,bij≥0.5,bjk≥0.5时有bik≥0.5,则称B有次序一致性。 从定义5能够帮助我们判断模糊互补矩阵是否具有次序一致性[21],但是如果方案较多时,直接进行判断不太容易,但是我们看到,次序一致性只关注被比较方案的优劣关系,而对优劣程度关心较少。因此,我们在研究模糊互补矩阵的次序一致性的检验和调整方法时,还需考虑方案之间的优劣程度,可以将模糊互补矩阵按照下列原则,转换成截集矩阵Bλ。 定义6[23]设B=(bij)n×n对任意的λ∈[0,1],称Bλ=(rij)n×n为模糊矩阵B的截集矩阵,其中 (1) 定义7[5]若次序一致性判断矩阵B,若xi优于xj,则对∀k有bik>bjk时,称B具有完全次序一致性。 定理2若对于任意的x,y∈X,若(x,y)∈R当且仅当y≥x,则(X,R)是偏序集。 证明(1)对于任意的x∈X,显然有x≥x,即同一个方案本身和本身能比较优劣,(x,x)∈R,即R满足自反性; (2)对于任意的x,y∈X,若(x,y)∈R且(y,x)∈R,则x≥y且y≥x,即方案x优于方案y且方案y优于方案x,因为方案一定是可比的,根据定义3得出bij≥0.5且bji≥0.5,根据定义4得bij+bji=1,所以,bij=0.5,bji=0.5,方案x和方案y一样好,x=y,R满足反对称性; (3)对于任意x,y,z∈X,若(x,y)∈R且(y,z)∈R,则x≥y且y≥z,即方案x优于方案y,方案y优于方案z,我们很容易判断出方案x优于z,x≥z,R满足传递性。 因此,R是X上的偏序关系,(X,R)是一个偏序集,证毕。 定理3给定偏序集(X,⪯),若Bλ(λ=0.5)是模糊互补矩阵B截集矩阵,则Bλ(λ=0.5)为偏序关系矩阵⟺B满足次序一致性。 证明⟹当Bλ(λ=0.5)为偏序关系矩阵,若sij=1,根据定义2可知,ai≥aj,根据定义3中(1)和(3)可知,bij≥0.5,所以当sij=1,sjk=1时,根据定义1中(3)可知,sik=1,自然得到bik≥0.5,又因为,bjk≥0.5,根据定义5可知,B满足次序一致性。 ⟸必要性:若bij≥0.5,由定义6可知,Bλ(λ=0.5)中,rij=1,所以当bjk≥0.5,rjk=1,因为B满足次序一致性,根据定义5,则bik≥0.5,则rik=1,满足定义1中的(3),又根据定理2中的(1)和(2),即本文所研究的模糊互补矩阵中方案都是可比的,所以满足定义1中的(1)和(2),因此,截集矩阵Bλ(λ=0.5)为偏序关系矩阵,证毕。 若截集矩阵Bλ(λ=0.5)为偏序关系矩阵,由定理1可知,按照公式(1)能转为hasse矩阵HR,因此,定理4给了我们一个的判断模糊互补矩阵B具有次序一致性的简单、便捷的方法,即按照定理1中的公式,Bλ(λ=0.5)偏序关系矩阵能转换为hasse矩阵HR,则该矩阵B具有次序一致性。那么,如果Bλ(λ=0.5)偏序关系矩阵不能转换为hasse矩阵HR,则矩阵B不具有次序一致性。 定理4给定偏序集(X,⪯),模糊互补矩阵B满足完全次序一致性的充要条件是任意截集矩阵Bλ(0.5≤λ≤1)满足传递性。 证明⟹对于B的任意截集矩阵,当x1>xj,bij>0.5,假设xj>xk,bjk>0.5时,因为模糊互补矩阵B满足完全一致性,根据定义7,xi优于xj时,bik>bjk,所以bik>bjk>0.5,因此根据定义1中(1)可知,xi>xk,满足定义1中(3)的传递性。 ⟸任意截集矩阵Bλ(0.5≤λ≤1)满足传递性,根据定义1中(3)可知,当xi>xj,如果xj>xk时,xi>xk,又根据定义3,xj>xk和xi>xk两两方案的优劣程度用实数表示为bik和bjk,所以,确保这种传递关系在截集矩阵Bλ(0.5≤λ≤1)中成立,当xj>xk优劣关系出现在Bλ(0.5≤λ≤1)截集矩阵时,即bjk≥λ,xi>xk优劣关系在Bλ(0.5≤λ<λ1≤1)截集矩阵已经出现便可,即bik≥λ1,又因为λ1>bjk≥λ,所以bik>bjk,证毕。 定理5给定偏序集(X,⪯),设Bλ(λ>0.5)为截集矩阵,若Bλ满足传递性,则Bλ+I为偏序关系矩阵。 证明⟹因为Bλ(λ>0.5)满足传递性,Bλ∈Bλ+I,因此在Bλ+I中,这种传递关系依然存在,即根据定理2中(3)可知,若xi>xj,xj>xk,则xi>xk所以Bλ+I满足传递性,又根据定义6可知Bλ中方案满足xi>xj(i≠j),则rij=1,I中方案满足xi=xj(i=j),rij=1所以Bλ+I中方案满足xi≥xj,则rij=1,xi ⟸若Bλ+I为偏序关系矩阵,在Bλ+I中,根据定义1中(3),若xi>xj,xj>xk则x1>xk又根据定义6可知,bij>λ,bjk>λ,bik>λ,截集矩阵Bλ按照定义6亦满足bij>λ,bjk>λ,bik>λ,又因为λ>0.5,则根据定义3中(1)可知,方案xi优于方案xj,方案xj优于方案xk,则方案xi优于方案xk,所以根据定义1中(3)Bλ满足传递性,证毕。 因此,模糊互补矩阵次序一致性检验和调整步骤: 第一步:首先求出模糊互补矩阵B的截集矩阵Bλ(λ=0.5),如果其可以转换为hasse矩阵,则Bλ具有次序一致性,如果不能转换为hasse矩阵则转为第二步; 第二步:把模糊互补矩阵B中大于等于0.5的元素按降幂排列,然后逐个检查截集矩阵Bλ(0.5≤λ≤1)递性,若某个截集矩阵Bλ(0.5≤λ≤1)不能转换为hasse时,则进入调整1,若所有截集矩阵Bλ(0.5≤λ<1)都能转换为hasse时,完毕; 调整1画出偏序关系矩阵,Bλ的关系图,检验Bλ的关系图新增的箭头线是否有回路rki,如果有,则把回路rki去掉,Bλ矩阵rki元素变成0,B中bki=1-bik,返回到第二步,如果不存在回路rki,则进入调整2; 调整2在Bλ中把rik从0改成1,rki变为0,B矩阵中相应的元素变成1>bik≥λ1>1的任何数,返回到第二步。 算例1某公司准备给某个项目投资一笔钱以获得效益最大化,公司聘请一名专家对方案集X={x1,x2,x3,x4}进行决策[18],这四个项目分别是:x1企业行业,x2是房地产行业,x3是电子行业,x4是奶制品行业。专家给出的模糊互补矩阵为: HR=(B0.5-I)(B0.5-I)2 能转换为hasse矩阵,所以该模糊判断矩阵具有次序一致性,和文献[1]中的结论一样。 算例2假设专家针对算例1给出的模糊判断矩阵为: HR=(B0.5-I)-(B0.5-I)2 第二步:把矩阵B中的≥0.5元素从大到小排列为0.9>0.8>0.7>0.6<0.5。根据定理5: B0.9关系图如图1所示: 图1 B0.9关系图 B0.8关系图如图2所示: 图2 B0.8关系图 新增加的关系是方案2到方案3的关系r23,并不存在回路,进入调整2,将B0.8中的r24调整为1,将B中的b24元素变为0.9 B0.7关系图如图3所示: 图3 B0.7关系图 Y=B0.6关系图如图4所示: 图4 B0.6关系图 Y=B0.6不能转换成hasse矩阵,进入调整1,图3和图4相比较,新增加r42回路,所以去掉r42回路,B中的b42修改为1-r42=0.05,B0.6中的r42调整为0,新增方案1到方案3的关系r13,根据调整2,把r34修改为0.6,保证r14>r34,把r23修改为0.92,保证r23>r21,返回到第二步,根据定理4: HR=(B0.5-I)-(B0.5-I)2 在实际决策中,决策者给出的模糊判断矩阵很难满足完全一致性,却能给出具有次序一致性的矩阵,由次序一致性矩阵给出排序向量具有很好的可信度[5],本文在讨论模糊矩阵次序一致性分析必要性和现有判断矩阵次序一致性研究成果存在缺陷的基础上,首先,给出了模糊互补矩阵B0.5能转换为hasse矩阵,则其满足次序一致性的检验定理,其次,给出了模糊互补矩阵满足完全次序一致性和任意截集满足传递性(截集矩阵Bλ+I能转换为hasse矩阵)的等价性的检验定理,即通过调整模糊互补矩阵的所有λ≥0.5截集矩阵满足传递性,使其满足完全次序一致性,之后,给出了检验和调整模糊判断矩阵次序一致性的步骤,最后通过两个算例进行了验证。通过算例,我们发现该检验和调整方法简单、不丢失信息、直观、易操作、鲁棒性好。与文献[15]的方法相比,首先,本文方法在增加了加上条件“若xi优于xj,则对∀k都有bik≥bjk”时,两种方法等价;其次,本文也解决了一致性的悖论,不仅利用偏序关系矩阵来判断互补的次序一致性,检验直观,而且还利用偏序关系矩阵把互补判断矩阵调整到完全次序一致性。徐泽水给出了模糊互补矩阵和互反判断矩阵的转换公式[24],因此,本文的方法还可以推广到互反判断矩阵。2 模糊互补矩阵次序一致性偏序集检验与调整
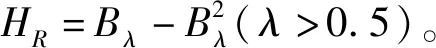
3 算例分析

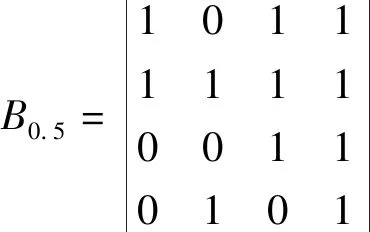
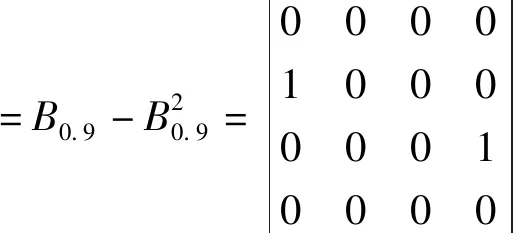
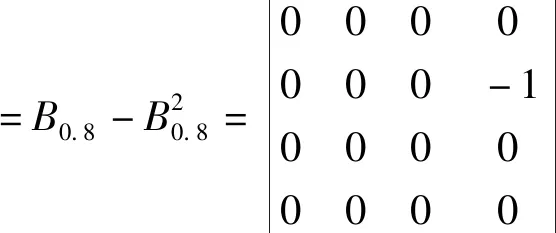
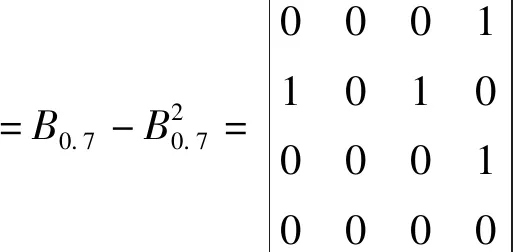

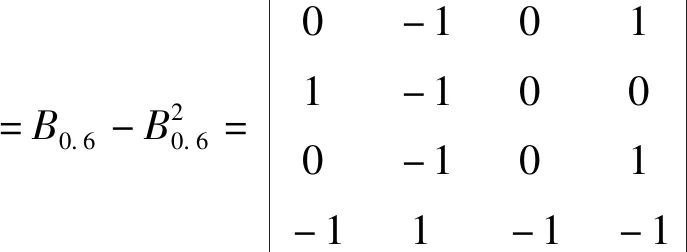

4 结论

