考虑情绪因素的城市拆迁RDEU博弈模型与系统脆性分析

熊国强， 张 毅

(西安理工大学 经济与管理学院，陕西 西安 710048)

0 引言

随着我国工业化和城镇化进程的加速，城市发展用地规模明显不足，以往城市各功能区的空间布局随着发展的需要也亟待进行调整。如何重新整合已有资源，提高土地利用效率，缓解城市横向发展空间不足等问题便显尤为迫切。近年来，全国许多城市陆续开展了对老街区、城中村、棚户区以及地铁沿线的拆迁改造工作，然而拆迁工作纷繁庞杂，涉及利益群体众多，是一个复杂的系统工程，各方对自身损益都颇为敏感，利益分配稍有偏倚，群体情绪便极易受到挑拨，拆迁纠纷就可能发展为群体性冲突。因此，深入剖析各利益相关方的行为规律，揭示城市拆迁纠纷引发群体性冲突的内在机理成为亟待研究的重要问题。

近年来，国内外学者对城市拆迁纠纷所引发的群体性冲突进行了一定研究。一些学者认为当前城市拆迁纠纷不断，拆迁冲突频发，其症结主要在于利益之争并从博弈论角度分析了城市拆迁相关方的行为特征。杨青等建立了城市拆迁的零和博弈模型，研究发现拆迁人和被拆迁人之间存在竞争地位的优劣势，博弈的占优策略使得拆迁双方都不能得益，必须通过政策干预来影响博弈的可能解[1]。唐代中等建立了城市拆迁补偿的演化博弈模型，分析了不同收益情况下的演化稳定策略[2]。刘德海等运用情景分析法定义了两种城市拆迁模式，建立了地方部门与城市住户间的博弈均衡演化模型，分析了两种拆迁模式之间相互竞争的均衡演化方向[3]。申海成构建了包含拆迁人、被拆迁人、中介机构和政府四方的博弈模型，分析了拆迁人和被拆迁人、中介机构的博弈均衡[4]。但是，经典博弈理论囿于参与人完全理性假设，难以解释诸多“非完全理性”因素对行为人决策的影响，分析结论与现实中人们的直观感受往往不符。大量实验研究和反例分析表明，博弈论的根基期望效用理论(简称EU理论)存在缺陷问题[5]。Quiggin提出的RDEU理论(Rank-Dependent Expected Utility Theory，简称RDEU)引入非线性概率函数能够克服EU的局限性[6]。熊国强基于RDEU理论构建了非期望效用下的RDEU博弈模型，揭示了博弈问题的纳什均衡与局中人情绪因素的相关性[7]。文献[8]建立了RDEU鹰鸽博弈模型，研究了局中人情绪因素对均衡解的影响。目前，基于RDEU理论建立博弈模型研究拆迁冲突问题的文献鲜有见到。

城市拆迁博弈作为复杂社会系统的一个子系统，由拆迁纠纷引发群体性冲突的过程也是一个复杂系统的脆性激发和演化过程，当其遭受足够大的打击而崩溃时，由于各子系统间的脆性关联性，其破坏性的演化行为最终会波及整个社会系统。也可以说，城市拆迁可能成为诱发巨大社会灾害的脆性源。一些学者已经将复杂系统脆性理论应用到了突发事件或事故的脆性风险研究之中。林德明等构建了基于一维元胞自动机的脆性演化规则并用其对传染病在全国的大规模扩散进行了仿真分析[9]。吴红梅等通过建立风险熵函数研究了煤矿事故系统的脆性风险[10]。刘明等从非合作博弈视角研究了船舶电力的系统脆性问题[11]。阎耀军等基于支持向量机模型的脆性熵评价方法研究了公共危机事件的脆性风险预警问题[12]。但是，从复杂系统脆性角度研究城市拆迁冲突的脆性演化规律，目前尚未见到相关研究成果。

本文将RDEU博弈模型与复杂系统脆性理论集成来研究城市拆迁冲突的演化问题，首先基于RDEU理论将人的情绪因素融入期望效用函数之中，分别给出了地方政府、被拆迁人的RDEU期望收益函数，以此建立了城市拆迁RDEU博弈模型；根据博弈双方的情绪状态，通过求解最优反应条件，分析了被拆迁人采取抗争和地方政府采取强拆两种极端行为的条件和行为趋势；基于熵和初等元胞自动机建立了城市拆迁系统的脆性演化规则，并利用该规则分别模拟了两种极端行为下城市拆迁冲突的脆性激发演化过程，最后提出了相应的对策建议。

1 城市拆迁RDEU博弈模型

1.1 博弈的基本要素

在城市拆迁中，多由地方政府主导实施，在拆迁完成后再进行地块的出让。由于在拆迁中并未直接涉及开发商的利益，因此，博弈主体为地方政府(G)和被拆迁人(R)。设城市拆迁冲突中，地方政府选择“强拆”和“妥协”两种策略，强拆策略是指对被拆迁人给与一定的补偿并进行强制拆迁，妥协策略是指同意被拆迁人要求的补偿标准再进行拆迁。被拆迁人有“抗争”和“合作”两种可选策略，抗争策略是指要求地方政府给出更高的补偿标准并拒绝拆迁，合作策略是指同意地方政府给出的补偿标准并积极配合拆迁活动。

这样，地方政府(G)的策略集S1包括“强拆”策略F和“妥协”策略C，记为S1={F，C}。被拆迁人(R)的策略集S2包括“抗争”策略P和“合作”策略A，记为S2={P，A}。城市拆迁冲突的博弈收益矩阵如表1所示。

表1 地方政府与被拆迁人的博弈收益矩阵

其中，V1为城市拆迁中地方政府所得收益，政府作为经济人，其所得收益V1由经济利益与政治利益两部分共同组成，一方面通过城市拆迁获得财政收入，促进地区经济增长，另一方面，地方政府也会同时考虑拓展政绩的政治利益。V2为被拆迁人得到的收益，房屋拆迁必然会改变被拆迁人的现有生活状况，他们的收益体现在居住利益和财产利益中。ΔV1是地方政府采取强拆且以低于市场价值进行补偿，在出让土地后所带来的超额利润，目前许多地方政府依赖土地财政，为了获得超额利润，往往忽略住户土地使用权让渡等增值因素以低于市场价值进行补偿，甚至借助公权力和专政机关的力量强行拆迁与民逐利。V为地方政府采取强拆策略而受到的惩罚成本，为了维护自身利益，被拆迁人可能采取上访抗争策略进行反抗，地方政府既会受到上级政府的惩戒，又要承担强拆给住户所带来的损失。ΔV2为被拆迁人上访抗争所得的补偿。C1为地方政府妥协策略下被拆迁人抗争的成本，C2为地方政府强拆策略下被拆迁人抗争付出的成本。

随着城市居民自主意识的崛起，当被拆迁人的合法利益受到侵害时，被拆迁人会选择网络媒体曝光和上访维权等途径维护自身合法权益，政府采取强拆不仅将招致其政治声誉受损、公信力下降，还得不到差级地租ΔV1以及赔偿强拆给住户所带来的损失ΔV2，即有V>ΔV1+ΔV2。

当地方政府采取强拆策略时，被拆迁人抗争所付出的成本往往很大，甚至不惜以死相逼采取自焚等极端方式，有C2>ΔV2。而在地方政府妥协情况下，被拆迁人选择抗争的方式相对会比较平和，所付出的成本C1也就较小，则有ΔV2>C1。

因此，上述量值之间存在以下关系：

V1+ΔV1>V1>V1-ΔV2>V1+ΔV1-V

(1)

V2+ΔV2-C1>V2>V2-ΔV1>V2+ΔV2-ΔV1-C2

(2)

1.2 构建城市拆迁的RDEU博弈模型

假设地方政府G的混合策略为 (p，1-p) ，即政府以概率p选择“强拆”，以概率1-p选择“妥协”；被拆迁人R的混合策略为 (q，1-q) ，即被拆迁人以概率q选择“抗争”，以概率1-q选择“合作”。考虑到情绪对城市拆迁博弈的现实影响，在博弈结构中引入反映参与者情绪状态的情绪函数，设地方政府G的情绪函数为w1(p)=pr1，被拆迁人R的情绪函数为w2(q)=qr2，其中r1，r2>0，分别称为地方政府G和被拆迁人R的情绪指数。

由博弈收益矩阵表1看出，城市拆迁双方博弈过程中，有{强拆，抗争}、{强拆，合作}、{妥协，抗争}、{妥协，合作}四种策略组合，每个博弈方都具有四种可能收益，根据RDEU理论模型，可以得到地方政府G和被拆迁人R获得相应收益时的概率分布、秩位及决策权重，如表2和表3所示。

表2 地方政府G收益值对应的概率分布、秩位及决策权重

表3 被拆迁人R收益值对应的概率分布、秩位及决策权重

因此，地方政府G所对应的RDEU期望收益函数为

UG=(V1+ΔV1)w1(p-pq)+V1[w1(1-q)-w1(p-pq)]+(V1-ΔV2)[w1(1-pq)-w1(1-q)]+

(V1+ΔV1-V)[1-w1(1-pq)]

=ΔV1(p-pq)r1+ΔV2(1-q)r1+(V-ΔV1-ΔV2)(1-pq)r1+(V1+ΔV1-V)

(3)

同理，可得被拆迁人R的所对应的RDEU期望收益函数为

UR=(V2+ΔV2-C1)w2(q-pq)+V2[w2(1-p)-w2(q-pq)]+(V2-ΔV1)[w2(1-pq)-w2(1-p)]+

(V2+ΔV2-ΔV1-C2)[1-w2(1-pq)]

=(ΔV2-C1)(q-pq)r2+ΔV1(1-p)r2+(C2-ΔV2)(1-pq)r2+(V2+ΔV2-ΔV1-C2)

(4)

至此，本文建立了城市拆迁问题的RDEU博弈模型，有如下定义。

定义1城市拆迁的RDEU博弈模型为R(S1,S2;UG,UR)，其中S1，S2分别是地方政府G和拆迁人R的混合策略集，UG，UR为地方政府G和拆迁人R的RDEU期望收益函数。

下面给出RDEU博弈模型混合策略下的Nash均衡定义。

定义2城市拆迁的RDEU博弈模型R(S1,S2;UG,UR)，如果存在混合策略组合{(p*,1-p*)，(q*，1-q*)}，简记为(p*，q*)，∀p,q∈[0,1]，使得下面不等式成立，即

UG(p,q*)≤UG(p*,q*)≤UG(p*,q)

UR(p,q*)≤UR(p*,q*)≤UR(p*,q)

则称(p*，q*)为R(S1,Sj2;UG,UR)的混合策略Nash均衡。

2 情绪对RDEU博弈模型Nash均衡的影响分析

根据Nash均衡求解的基本方法，当城市拆迁博弈双方都采用混合策略时，对地方政府和被拆迁人的RDEU期望收益函数(3)和式(4)，分别对p和q求偏导，得到

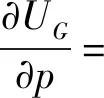
(V-ΔV1-ΔV2)r1q(1-pq)r1-1

(5)

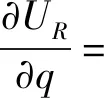
(C2-ΔV2)r2p(1-pq)r2-1

(6)

令偏导(5)、(6)同时为0，得到城市拆迁RDEU博弈模型的纳什均衡解满足的条件：

ΔV1(p-pq)r1-1(1-q)-(V-ΔV1-ΔV2)q(1-pq)r1-1=0

(7)

(ΔV2-C1)(q-pq)r2-1(1-p)-(C2-ΔV2)p(1-pq)r2-1=0

(8)

可以看出，方程组(7)、(8)是一个超越方程组，难以求得其解析解，但可以从典型情形进行讨论。在现实中，城市拆迁博弈双方的情绪状态可能不一致，如一方存在情绪而另一方理性，或博弈双方都存在情绪。限于篇幅和考虑现实情景，本文主要对博弈双方都受情绪因素影响的情形进行讨论。

博弈双方都受情绪因素影响下，即有r1≠1,r2≠1，地方政府和被拆迁人相应的最优反应函数分别为：

(9)

(10)

命题1对城市拆迁的博弈模型R(S1,S2;UG,UR)，当C2>ΔV2，ΔV2>C1时，无论博弈双方为哪种情绪状态，则总存在两个纯策略Nash均衡{妥协，合作}和{强拆，抗争}。

证明由式(9)和(10)看到，当C2>ΔV2，ΔV2>C1时，不论博弈双方的情绪指数r1与r2如何，如果地方政府选择强拆的概率p=1，则被拆迁人相应的最优反应选择是q=1，即(p*，q*)=(1，1)，故存在纯策略Nash均衡{强拆，抗争}。

同理，有(p*，q*)=(0，0)，即存在纯策略Nash均衡{妥协，合作}。

下面讨论博弈双方采用混合策略的情况，在(9)和(10)两式中，我们将p，q分别看作为r1，r2的函数，这时，p受到r1的影响，记为p(r1)，q受到r2的影响，记为q(r2)。

对p(r1)和q(r2)分别关于r1，r2求一阶导数，通过分析p′(r1)和q′(r2)的变化来观察函数p(r1)和q(r2)曲线的变化，从而可了解情绪指数r1，r2的不同状态对p，q的影响。可得:

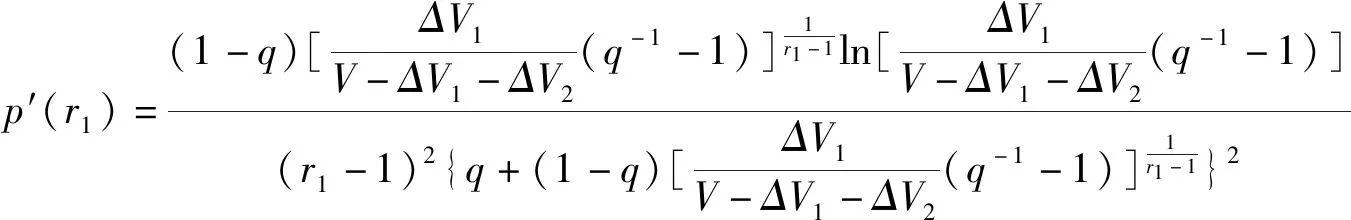
(11)

(12)

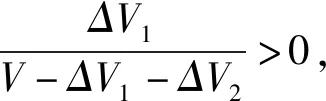
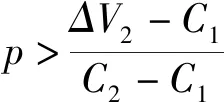
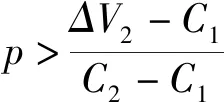
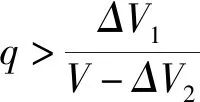
这一理论结果正好说明了现实生活中城市拆迁纠纷之所以会演化为群体性冲突正是博弈双方受“悲观”等非理性情绪因素影响的结果，诸多群体性冲突的典型案例也表明悲观情绪对纠纷升级为对抗冲突有着内生的驱动作用。

3 城市拆迁的系统脆性分析

虽然上述RDEU博弈模型R(S1,S2;UG,UR)描述了城市拆迁利益相关方的博弈结构和行为策略，可以揭示不同情绪状态下城市拆迁纠纷内生为对抗冲突的演化行为，但是从复杂系统视角看，城市拆迁仅是社会系统的一个子系统，城市拆迁博弈行为对社会系统的其它子系统可能产生连锁影响，甚至城市拆迁对抗升级可能导致整个社会系统的崩溃，RDEU博弈模型难于刻画这种复杂系统的耦合关系。基于RDEU博弈模型视角的局限性，下面尝试将RDEU博弈模型与复杂系统的脆性理论集成来研究情绪因素影响下城市拆迁冲突的系统脆性激发过程。

3.1 系统脆性的熵

城市拆迁是个系统工程，它不仅仅是拆迁，还涉及被拆迁人的就业、入托上学、老人瞻养、城市低保以及城市交通等诸多社会问题，在城市拆迁由纠纷演化为群体性冲突的过程中往往伴随有上访、封桥堵路和打砸抢烧等暴力行为，这时城市拆迁的系统脆性被全面激发，由于社会系统的各子系统间进行着各种物质能量的交换，因此它的崩溃会导致其他子系统的有序状态也遭到破坏，这种连锁反应就如同多米诺骨牌，一经触发会自动依次递推下去直至整个社会系统崩溃，这种系统崩溃的特性称之为系统脆性。

熵可以用来量化评价城市拆迁系统脆性的程度。基本思想是：城市拆迁系统遭受足够大的外力冲击而崩溃的过程所表现出的正是系统内熵增的过程，由于系统的自组织性，城市拆迁系统会向与其相邻的社会各子系统(如城市交通子系统和国民经济子系统)吸收负熵流以减缓熵增速度，尽力维持原有的内部秩序。然而相邻子系统向外输出负熵流的同时也引起了自身熵增速度加剧，其所能够提供的负熵流会越来越少，得不到外来负熵的平抑，城市拆迁系统内部熵增速度会逐渐加快最终走向崩溃。相邻子系统受其所累又会陷入这种外部负熵供应不足，内部熵增速度加剧的境地直至崩溃，各系统间的耦合会使这种连锁循环效应依次传导直至整个社会系统崩溃。

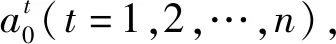
(13)

那么，a0在t时段的状态熵[13]为

(14)

其中K为常数。

当城市拆迁由拆迁纠纷开始向拆迁冲突演化时，博弈双方采用混合策略情形下呈现的是“强拆”和“抗争”状态，由前文分析知，每种状态的概率分别为p(r1)和q(r2)，其中p、q分别受到情绪r1与r2的影响，于是，a0的初始状态为

(15)

于是，a0对应的初始状态熵为：

(16)

设a-1，a1在t时刻提供的负熵流分别为

(17)

(18)

其中，g(x,y)是连续单调递减函数，对任意x，y有g(x,y)>0。

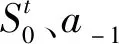
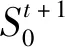
(19)

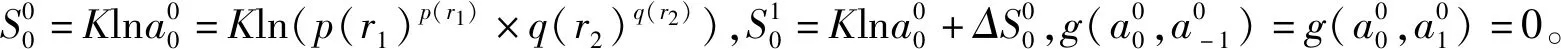
3.2 系统脆性的演化规则

本文采用初等元胞自动机建立系统的脆性演化规则，并据此模拟城市拆迁系统的脆性演化行为。元胞自动机是一种有自组织行为的时空离散、状态离散的并行数学模型。其基本思想是：元胞当前自身的状态与其邻居的状态共同决定下一时段元胞的状态[14]。元胞状态演化的函数称为状态演化函数，也就是系统的演化规则。初等元胞自动机是常用的一种元胞自动机模型，它的元胞状态只有2个，邻居半径为1，元胞都遵循同样的演化规则。

(20)

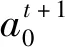
(21)

可以验证，该元胞自动机为合法元胞自动机。

根据式(19)，由下向上依次递归进行迭代得：

(22)

则得城市拆迁的系统脆性演化规则：

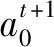
(23)

4 系统脆性的模拟分析

依据某地城市拆迁的补偿政策，博弈的收益矩阵中各要素的值分别设为：V1=10万，V2=6万；ΔV1=4万，V=11万，ΔV2=4万；C1=3万，C2=5万。可以看到，各要素量值之间满足式(1)和(2)，则有

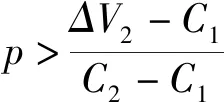
不妨假设地方政府选择强拆策略的概率为p=0.52，此时p为一定值，q(r2)为情绪的函数。为反映悲观情绪的加剧对被拆迁人行为影响的动态过程，情绪指数r2分别取0.9和0.8。

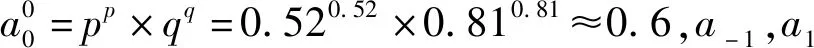
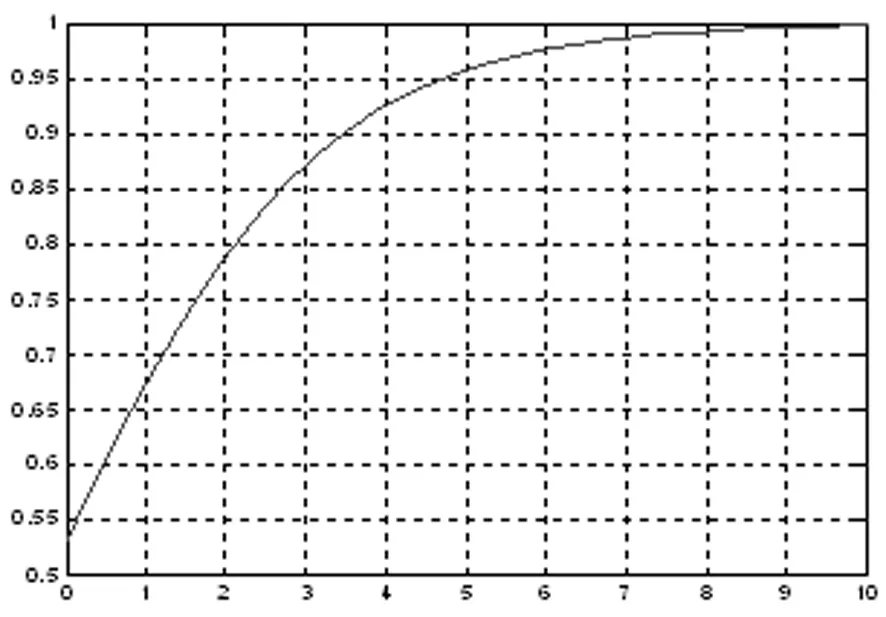
图1r2=0.9时a0的状态曲线

图2r2=0.8时a0的状态曲线

比较图1和图2可以发现，当r2=0.9时，系统演化到t=9时，a0崩溃。而随着悲观情绪的加剧(r2减小到0.8)，系统演化到t=6，a0就崩溃了。这表明随着被拆迁人悲观情绪的加剧，城市拆迁系统崩溃所需的时间也缩短了，也就是说，城市拆迁纠纷演化为对抗冲突的速度加快了。这一结果正与社会实际相吻合，即当地方政府选择强拆策略，随着被拆迁人悲观情绪的不断加剧，而管理部门又不能及时发现和疏导被拆迁人的悲观情绪，并与被拆迁人进行沟通，其结果就是拆迁纠纷以更快地速度演化为对抗冲突。

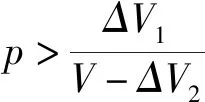
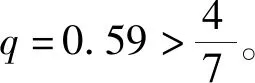
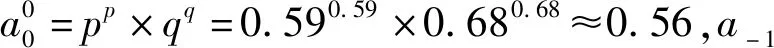
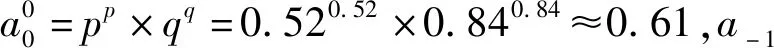
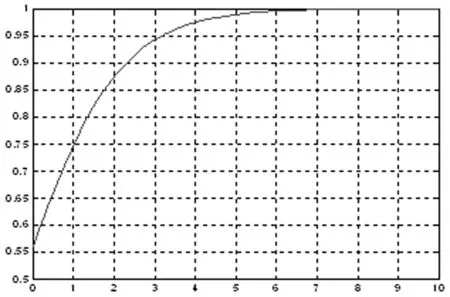
图3r1=0.9时a0的状态曲线

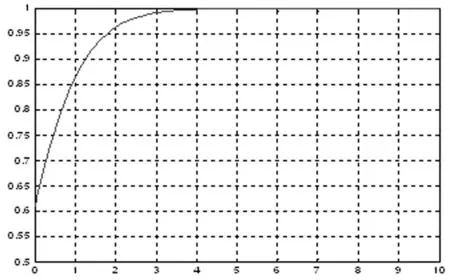
图4r1=0.8时a0的状态曲线

由图3和图4可以看到，在情绪指数r1=0.9时，系统演化到t=7时，a0趋于崩溃。而当r1=0.8时，系统演化到t=4时，a0就崩溃了。结果表明，随着地方政府悲观情绪增强，城市拆迁系统崩溃的时间缩短，拆迁纠纷演化为对抗冲突的速度加快了。

5 结论与建议

本文基于新的RDEU理论将参与人的情绪因素融入期望效用函数之中，建立了城市拆迁的RDEU博弈模型，讨论了情绪影响之下被拆迁人采取抗争策略和地方政府采强拆策略的行为演化规律。基于熵和初等元胞自动机理论建立了城市拆迁的系统脆性演化规则，模拟了城市拆迁由纠纷演化为对抗冲突的脆性激发过程。研究结果表明：无论是被拆迁人还是地方政府，当他们具有“悲观”情绪时，随着情绪的加剧，他们采取强硬策略相互对抗的可能性也会越来越大，悲观情绪也会使城市拆迁系统崩溃所需的时间缩短，拆迁纠纷会快速演化为对抗冲突。

本文研究结论可为处置城市拆迁冲突提供一些有益的启示。政府部门或社会应把握时机向城市拆迁系统及时地引入负熵流(如信息流)，疏导被拆迁人的悲观情绪，避免拆迁纠纷升级为对抗冲突。因此，社会相关方在城市拆迁管理过程中应注意以下几点：

(1)在城市拆迁中，当拆迁纠纷发生时，博弈各方的情绪神经都极易受到刺激，双方都应保持克制而不是单方面采取极端做法，避免触动对方反抗底线使事态升级恶化。

(2)应建立健全低成本、常态化、快速化的利益诉求表达机制，保证信息传递渠道的畅达。拆迁系统的脆性被激发后，内部熵增很快，为了维持本系统的稳定它会不断地从外界吸收负熵流，这一连锁效应会直接波及其它社会子系统。此时避免拆迁纠纷发展为群体性冲突的理想办法就是向拆迁系统充分地引入负熵流。譬如保障信息流的充分注入和高效输出是降低系统无序化程度，形成能量反馈回路，从而快速平息事态的重要举措。因此，通过建立高效畅通的信息传递渠道，快速反映各方的利益诉求，避免因信息缺失所导致的误解。此外还应注意规范媒体信息报道，引导舆论宣传导向，打击蓄意煽动和谣言传播，为真实信息传递扫清障碍。

(3)完善突发事件的监控预警，及时反馈事态动向，把握化解矛盾的有效时机。由于拆迁纠纷升级为对抗冲突的脆性演化很快，冲突一旦爆发相关管理部门很难在短时间中给出较好的解决办法，因此在城市拆迁实施前，地方政府应进行广泛的听证调研，积极鼓励各方表达意见，通过协调使拆迁的政策目标最大化满足各方利益，尽量避免因政策失当所引发的群体性事件。拆迁纠纷一旦显现出升级的迹象，应做好可能引发群体性冲突的态势评估工作，提早启动监控预警机制，及时反馈各方动向。

(4)应实时监测、评估各方的情绪反应，及时疏导参与人的不良情绪，诸如猜疑、忧虑、不公平感等悲观情绪的滋生蔓延，如果参与人不良情绪难以通过正常渠道得到合理宣泄，必然会从其它途径寻求突破，非理性决策的结果往往是通过各种偏激手段以抒胸中块垒。值得注意的是参与人的悲观情绪常常容易引起其他个体的同情，并通过各种社会关系传染给其他个体，产生群体性集合行为。因此不妨依靠社区组织、民间团体等群众自组织的力量密切关注被拆迁人的心理和情绪反应，加强舆论引导和心理干预，排解被拆迁人的悲观情绪，以使事态得到有效控制。