基于数值分布的激励型综合评价方法
许世存, 易平涛, 郭亚军, 宫诚举
(1.东北大学 工商管理学院,辽宁 沈阳 110169; 2.哈尔滨工程大学 经济管理学院,黑龙江 哈尔滨 150001)
0 引言
综合评价是指对被评价对象所进行的客观、公正、合理的全面评价[1~3]。随着科学技术的日益进步,数据和信息量的急剧增加,综合评价被广泛应用于众多领域。激励评价是综合评价的一个重要分支,所谓激励,就是需求者以追求某种利益为目的,使执行者具有能够完成该目的的积极性和内在推动力,这种积极性和内在推动力的产生,通常是靠科学、合理、公正的激励方法来实现的。目前有关激励评价方法的研究已取得丰硕的成果,文献[4]利用被评价对象在不同时段的增益水平确定优劣激励点进而得出激励结果。文献[5]通过设置两条正负激励控制线来实现对不同被评价对象的奖惩。文献[6]针对双激励控制线的不足,提出了具备“状态激励”和“趋势激励”的泛激励控制线多阶段信息集结方法。文献[7]在泛激励控制线的基础上,通过对指标的综合修正来实现对多指标的动态奖惩。文献[8]从动态评价的角度将被评价对象在不同时间点的信息集结起来,引导被评价对象实现更高层次的突破,文献[9]和文献[10]是在传统密度算子中将激励因素考虑进去,从静态评价的角度对被评价对象在某一时点的状态进行评价。
数值分布是指一组给定的离散数据在某一区间不同位置的分散或集中程度;等级区间的划分(简称等级划分)是指根据数值分布情况将某一区间划分为若干互不相交的子区间。等级区间划分的结果不同,得到的综合评价结果亦不相同,因而如何科学的划分等级区间是综合评价需要考虑的重要问题。
针对目前已有文献总结出以下几个问题:(1)目前对于等级的划分方法通常是事先人为确定好相邻等级区间的分界点,然后按照数值的大小将其归类到应属等级。然而该方法存在以下两点不足:①忽略了数值的实际分布情况。即相邻等级区间的分界点完全是由评价者事先主观给定的,缺少对数据实际分布情况的考虑;②缺少对各被评价对象在数值上的比较。已有的等级划分方法对每个被评价对象的等级划分都是独立完成的,也就是说,每个被评价对象的等级划分结果都是孤立的,这种不涉及与其他被评价对象进行比较的结果往往会使其他被评价对象不以为然,难以站稳脚跟。(2)对等级权向量进行归一化处理。若对没有达到高等级的被评价对象的等级权向量进行归一化处理,有可能会使其在低等级的权重过大,造成评价过程不具有公平性。下面通过一个例子来解释说明:例如有两个被评价对象和6个指标值,假设将指标值划分为4个等级,两个被评价对象的指标值及等级划分情况如表1所示。

表1 评价数据及其等级划分情况
从表1可以看出,两个被评价对象在等级2中的指标个数和指标值均相同,假设两个被评价对象经过归一化处理后的等级权向量分别为ξ1i(k=1,2,3,4)和ξ2j(j=1,2),由于等级权向量反映了等级的重要程度,因此等级权重是随等级的递增而递增的,所以两个被评价对象在等级2的权重ξ12和ξ22是不相同的,在这种情况下对被评价对象进行激励是不科学的,很难使被评价对象接受。
针对上述问题,本文提出了一种基于数值分布的等级划分方法,与现有的等级划分方法不同的是,该方法是将所有被评价对象的数值一起进行比较划分,并且具备能够根据评价者的需求来实现和调整数据间等级差异的功能;在此基础上对传统密度算子进行拓展,以实现对被评价对象进行科学、合理的激励为目的,确定指标权向量和等级权向量,从而形成一种基于数值分布的激励型信息集结方法,进而实现促进被评价对象的全面发展。
1 基于数值分布的等级划分方法
本文对被评价对象激励的原则是对各被评价对象处于高等级区间的指标进行较大的激励,对于处于低等级区间的指标进行较小的激励,因此需要对各被评价对象的不同指标值进行等级划分。
由于平均值可以衡量一组数据的一般水平,用平均值作为划分数值的依据即遵从了数值的实际分布情况,又体现了各数值之间的比较,此外评价者将等级总数设置的越大,可以突出数值间的等级差异。基于上述思想,本文对等级区间分界点进行调整,使其能够实现并调整数值间的等级差异。
记n个被评价对象o1,o2,…,on,在m个评价指标x1,x2,…,xm下的值经过预处理后的数值矩阵记为
假设共划分为q个等级,按照如下步骤对m×n个数据进行等级划分。
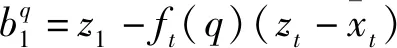
(1)
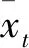
式(1)中的数值差异偏好系数ft(q)可按下式确定
(2)
式(2)中,mt为等级差异影响指数, 且mt>q,t=1,2,…,q-1。
(3)
因此可以通过调整St的取值来实现和调整数值间的等级差异,由式(3)可知St由mt唯一确定。
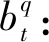

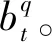
基于数值分布的等级划分方法的步骤:
步骤1确定等级总数q;

步骤3重复步骤2,直到将矩阵A中的数值划分出q个等级。
需要说明的是,并不是所有被评价对象的数值均分布于q个等级内,即某些被评价对象可能存在某一或某些等级区间内没有数值的情况。
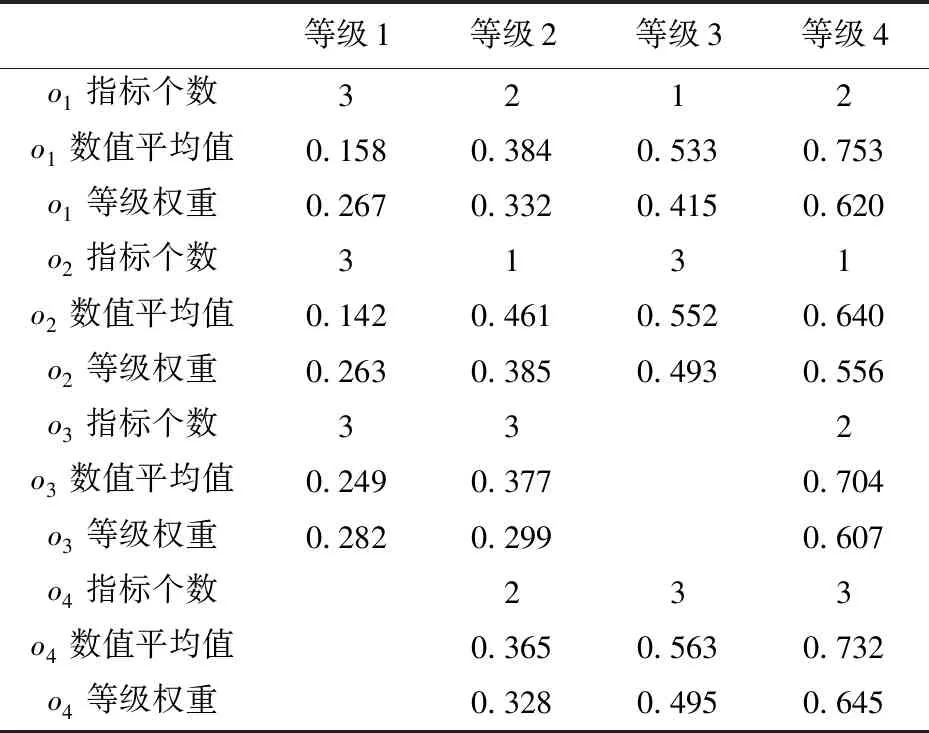
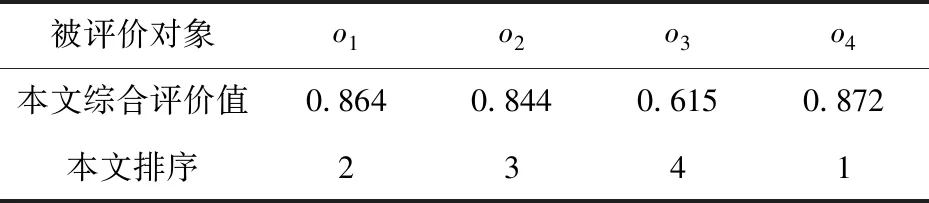
由于0 由等级区间划分的过程可知,任意等级划分时所用到的等级区间分界点都可作为该等级区间的上限和下一等级区间的下限,数值越远离其所属等级区间的下限且所处的等级越高,则应给予其更多的激励。下面根据上述思想确定指标权重。 设被评价对象的集合为O={o1,o2,…,on},评价指标的集合为X={x1,x2,…,xm}。为方便起见,记N={1,2,…,n},M={1,2,…,m}。被评价对象oi(i∈N)关于指标xj(j∈M)的预处理后的取值用xij表示,不失一般性,规定xij∈[0,1]。 定义2设共划分出q个等级(q>1),由低到高的等级系数分别用d1,d2,…,dq表示,称 μi=di/di-1,i=2,3,…,q (4) (5) 定义4设被评价对象oi(i∈N)关于指标xj(j∈M)的标准化数值xij被划入第t等级内,则称 (6) 为被评价对象oi(i∈N)关于指标xj(j∈N)在第t等级内的增长度,满足ρij[0,1]。 定义5设共划分出q个等级,被评价对象oi(i∈N)关于指标xj(j∈M)的标准化数值xij被划入第t等级内,则称 (7) (1)由于式(5)中分子的取值范围介于dt+dt-1到2dt之间,所以被划入t等级的指标的权重大于被划入小于t等级的指标的权重,从而突出了高等级指标的优势; (2)由式(7)可知wij是关于ρij的增函数,ρij越大,wij增大的速率就越大,从而实现了对同等级内指标的激励。 等级权重的确定应当结合等级系数、等级内指标的个数、等级内数值的均值大小来进行确定。对于处于低等级的数值,等级权重应与其中数值个数成反比关系,与数值均值成正比关系;对于处于高等级的数值,等级权重应与其中数值个数及数值均值成正比关系。本文基于上述思想对等级权重进行调整,以达到对被评价对象进行科学、合理激励的目的。 设被评价对象的集合为O={o1,o2,…,on},被评价对象oi(i=1,2,…,n)的指标值经过等级划分后,分布于l个等级(l≤q)。 定义7对于不同等级的权向量ξi=(ξi1,ξi2,…,ξil)T,称 p=1,2,…,l,t=1,2,…,q (8) 定理1等级权向量ξi=(ξi1,ξi2,…,ξil)T,当q>2时,恒有0<ξip<1(p=1,2,…,l)。 由定理1可知等级权向量不存在各等级权重在量级上相差不合理的情况,而在实际应用中为了突出数值的等级差异,等级的划分通常大于两个等级,为保证对被评价对象激励的公平性,所以不需要对等级权重进行归一化处理。 在确定了不同被评价对象的等级权重向量ξip=(ξi1,ξi2,…,ξil)T及指标权重向量wij=(wi1,wi2,…,wim)T的基础上可按“线性”和“积性”密度算子集结。 定义7称 (9) 定义8称 (10) 为带有激励作用的“积性”集结模型,式中字母含义与定义7相同。 为了验证本文研究方法的有效性,本文以文献[9]中的应用算例作参考,对本文提出的方法进行说明,具体计算过程如下: (1)用本文提出的等级划分方法对评价数据进行等级划分,设一共划分4个等级,这里取m1=6,m2=10,m3=20划分结果如表2所示。 表2 评价数值在各等级的分布情况 (2)根据式(5)确定出等级系数d1=0.173,d2=0.217,d3=0.271,d4=0.339,然后依据定义6的方法确定出各指标的权重,结果如表3所示。 表3 各被评价对象的指标权重 (3)根据定义7的方法确定各个等级的权重,结果如表4所示。 表4 各等级的权重 (4)用带有激励作用的“线性”集结模型对评价信息进行集结,求出各被评价对象的综合评价值和排序结果如表5所示。 表5 被评价对象的综合评价值及排序结果 本文提出的基于数值分布的激励型评价方法的激励原则是:对于不同等级区间,区间越高,对其进行的激励越大;对于同一等级区间中的不同指标值,指标值越大,对其进行的激励越大。与文献[9]相比,本文最大的区别在于指标值等级区间的划分,进一步得到的等级权重和指标权重也出现改变,因此相较于文献[9]中各被评价对象的评价值(0.592,0.489,0.513,0.629)、排序结果(2,4,3,1)和等级划分情况可以看出:首先本文提出的方法进一步提高了各被评价对象的评价值,所有被评价对象均得到了激励;其次被评价对象o2从第4名上升至第3名,原因在于被评价对象o2有一个指标从等级3上升到等级4,从而被给予较强激励,而被评价对象o3虽有两个指标从等级3上升到等级4,但有两个指标从等级2下降到等级 1,减弱了其上升的优势,从而激励力度不及被评价对象o2,因此综合评价后被评价对象o2超越被评价对象o3位居第3。因此可以看出,指标值的等级区间划分方法的不同会对等级权重产生影响,进而对指标权重产生影响并最终影响对被评价对象的激励程度,从而改变被评价对象的指标值和排序。 本文提出的基于数值分布的激励型综合评价方法具有如下的特点: (1)相比于现有的等级划分方法,本文采用的划分方法是基于数值的分布情况来确定等级区间分界点,可依照评价者的需求来调整数值间的等级差异,具有的主客观相结合的特征,在此基础上侧重各被评价对象之间的比较,使划分结果易于被接受; (2)在确定等级权向量时,解决了由于归一化带来的低等级权重过大的问题,使本文方法在评价的应用中更具有公平性; (3)利用本文提出的等级划分法确定出的等级区间分界点来确定数值的增长度,在此基础上进行指标赋权,使赋权结果更贴近实际情况,激励标准更加客观; (4)已有的密度加权向量是通过评价数值的疏密程度来确定的,而本文的等级权重向量在考虑数值疏密程度的基础上,又结合了等级系数和数值均值增加了激励的力度。2 指标权重的确定

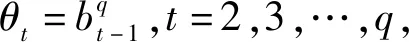
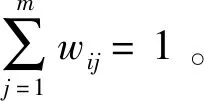
3 等级间评价信息的集结
3.1 等级权重的确定
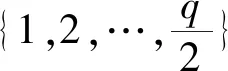
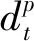

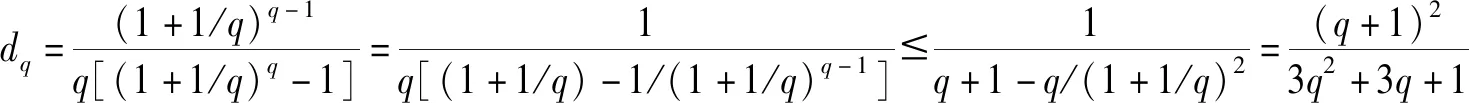
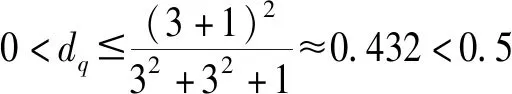
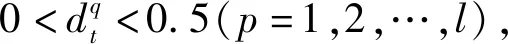
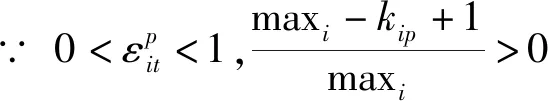
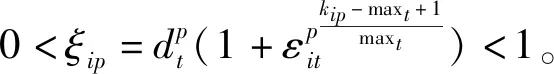
3.2 评价信息的集结
4 应用算例


5 结束语

