月面巡视器路径规划方法研究

于天一，费江涛，李立春，程 肖

（北京航天飞行控制中心，北京 100094）

引 言

我国成功实施了人类首次月球背面巡视探测活动，月球背面的复杂地形给月面巡视探测带来了更多的新挑战。在月面巡视器遥操作过程中，地面飞控人员需要根据科学探测目标进行遥操作任务规划，依据规划结果实施遥操作控制。路径规划是遥操作任务规划的重要组成部分，需要在任务规划过程中提供可通行性评估、行走策略制定等方面的技术支撑。

1 规划任务分解

月面巡视器的遥操作规划通常分为任务整体规划、探测周期规划、导航单元规划3个层次。

任务整体规划属于战略层面的规划，主要任务是对科学家提出的系列探测点进行初步评估，确定各探测点的探测顺序。探测周期规划属于事件级规划，主要解决从当前状态到完成一个科学探测点探测过程的规划。一般来说，科学探测点与巡视器所处位置通常距离数为几十米。受感知能力限制，巡视器每次移动距离一般不超过10 m，因此周期规划过程中需要将从当前点移动至探测点的过程分解成若干个导航点。路径规划在探测周期规划过程中依据地形和时变参数来确定导航点的位置。导航单元规划属于战术层面的规划，主要负责生成巡视器从当前点移动至下一导航点的控制计划和注入数据。路径规划在导航单元规划过程中负责规划行走路线，生成控制策略。

2 探测周期规划支持

探测周期规划需要确定每个行为的执行时间和地点。由于巡视器执行一个探测周期耗费的时间较长，因此在确定一个探测周期内各导航点的位置时，需要综合考虑光照、通信等时变因素和地形等非时变因素。

2.1 月面综合环境表达

月面环境通常采用栅格化的数字高程图来表达，通过提取和分析月面地形的坡度、坡向、阶梯障碍等相关特征[1]，处理转换成可供搜索的月面综合环境图。在探测周期规划过程中，既需要从空间维度对巡视器所处地形进行描述，又需要从时间维度对不同时刻巡视器所处的时变环境进行描述。可以建立月面环境立方模型，如图1所示，对时变和非时变环境进行描述。

月面环境立方有3 个维度，其中X和Y构成平面直角坐标系，表达巡视器所处的空间环境。T为时间维度，可以划分为多个层次，第1层为非时变层，该层内的栅格存储了由地形高程数据计算得来的巡视器行走代价信息，当某一点可通行时，其通行代价值的取值区间为[0，1），当不可通行时，通行代价值为1010；从第2 层开始为时变层，每一层代表某一个时间点上的时变信息，由于月球没有大气，因此不考虑太阳、地球等在不同角度下光照通信的差异。时变代价值采用二值法描述，0 表示时变代价满足，1 表示时变代价不满足。

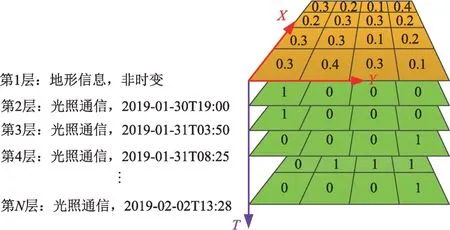
图1月面环境立方Fig.1 Lunar surface integrated environment cubic

2.2 时变信息计算

巡视器在月面探测过程中，主要考虑光照和通信2个方面的时变信息。

1）通视性分析

所谓通视性就是指给定视点和目标点，能否从视点直接看到目标点，即视点和目标点之间的地形和地物是否遮挡住了两者之间的连接线（即视线）。通视性原理如图2所示，如果能够通视，则视点和目标点连线上任意一点的高度都要大于两者之间对应位置的地形或地物高度。

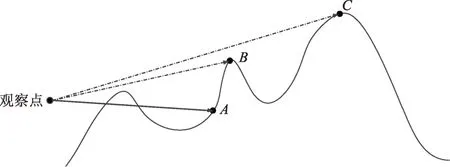
图2 通视性分析原理示意图Fig.2 Visibility analysis sketch

计算光照和通信情况时，可以将观察点分别设置为太阳和中继卫星的位置，此时视线是一组来源于太阳（或中继卫星）的平行光，其入射的高度角、方位角即为太阳（或中继卫星）的高度角、方位角。月面巡视器单次感知获得的地形数据通常在几十米范围内，采用通视性分析的方法可以解决几十米范围内的近距离地形遮挡问题[5]。

2）天际线分析

巡视器若在月球背面的环形山中着陆，四周远处的山脉不在巡视器感知地形范围内，却可能直接影响到巡视器的光照和通信，远距离地形的遮挡可以通过天际线分析的方法实现。

巡视器通过其所携带的相机进行环拍感知时，可以获得所处月面环境的照片。通过分析提取，再根据巡视器姿态和相机参数能够计算得出巡视器所处月面环境四周天际线的高度角和方位角。天际线的提取和高度角、方位角计算属于视觉测量范畴，具体计算方法详见参考文献[2]。

在某一特定地点，天际线高度角θl和方位角φl可以建立一一对应关系。因此，通过获取太阳星历可以计算得出任意t时刻太阳相对于巡视器所处月面的高度角θs(t)和方位角φs(t)，则基于天际线的光照代价Ctf计算方法为

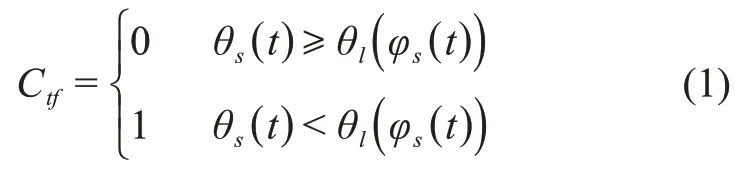
通信代价的计算方法与光照类似，只需将太阳星历替换为中继星星历。

3）时变步长设定

在月面巡视探测过程中，时间是连续变化量，光照和通信情况随着时间连续变化。为简化规划的求解难度，可以将光照和通信情况作为离散参数来考虑。比如，月面的太阳高度角大约每3 h变化1°，可以近似地认为3 h内的太阳光照情况不发生变化。因此，月面环境立方中时变信息可以按照一定的时间步长来进行分段式描述[6]。

2.3 导航点搜索

在探测周期规划过程中，导航点搜索需要综合考虑时变和非时变因素，因此采用多约束搜索方法进行路径搜索。多约束搜索以A*算法为基础，在进行代价计算时将时变和非时变代价均计算在内。

在A*算法中，某一点移动到相邻点的代价根据搜索策略的不同，通常为相邻点所在栅格的代价值，或者当前点到相邻点的欧几里得距离，或者为前两者的加权叠加。

在多约束搜索中，需要先明确巡视器在起点s开始移动的时刻t0，导航点间的期望里程d。计算从第i个点移动到其相邻点的代价时，需要考虑如下信息，一般的A*算法搜索过程中不需要记录里程信息，但在多约束搜索中，从起点移动至第i个点的里程信息Li关系到导航点的确定，如图3所示。当abs(Li%d)≤m时（m为栅格分辨率），则认为第i个点为导航点。

图3 周期规划中的起止点与导航点Fig.3 Start-stop points and navigation points in period planning

巡视器从起点移动至探测点过程中通常需要经过多个导航点，从离开一个导航点到移动至下一个导航点的过程，通常在几分钟内完成。相比巡视器在导航点上的停留时间，移动过程的时间消耗可以忽略不计。若设Δti为巡视器在第i个导航点上的预期工作时长，则从第i个点移动至相邻点的时刻为

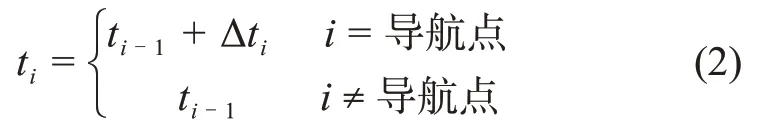
从第i个点移动至相邻点的非时变代价Cnt可以取当前点到相邻点的欧几里得距离。

从第i个点移动至相邻点的时变代价Crt为其相邻点在ti时刻的时变代价值。如前文所述，若Crt为0则认为相邻点的时变因素满足要求，否则认为不满足要求。

综上所述，从第i个点移动至相邻点的综合代价为

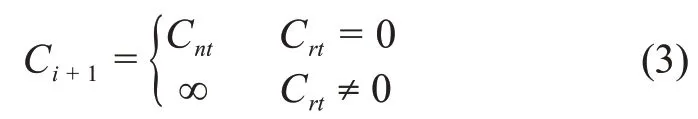
在探测周期规划过程中，根据获取的月面数字高程图和巡视探测区域内太阳和中继卫星的高度角与方位角信息，采用通视性分析和天际线分析等方法对时变参数进行分析计算，建立月面环境立方模型，采用多约束导航点搜索方法进行导航点确定。

3 导航单元规划

导航单元中路径规划负责计算从当前点到下一个导航点之间的行走路线。

3.1 搜索区域分割

对于轮式移动巡视器来说，行驶路径曲线存在拐点意味着两次行走控制之间需要增加原地转弯控制，原地转弯控制时车轮与月面钩挂风险相对较高且控制效率相对较低，因此月面巡视器的路径规划期望得到的是一条尽量平滑连续的行驶路径。当月面的障碍较多时，搜索得到的路径可能是一条复杂的曲线。为了简化问题的求解，可以将从规划起点到规划终点的区域划分成若干个区域，然后分别求解每个区域内的路径，再将各段路径连接起来得到整条规划路径。各区域的起点和终点统称为路径导引点。路径导引点可以从使用A*搜索算法获取到的路径点序列进行筛选得到。

1）导引点t提取

使用A*算法搜索得到路径点集合后，可以使用光束法提取路径导引点。提取路径导引点的原则是路径导引点尽量稀疏且相邻两点较容易到达。在工程处理过程中，为了使计算更加简捷高效，可以将路径导引点的提取标准修改为尽量稀疏且相邻两点直线可达。

2）可通行性判断

可通行性的判断可以使用计算机图形学中的Bresenham算法确定两个路径导引点之间经过的栅格，然后依次判断经过栅格的可通行性。Bresenham算法原理是过各行、各列像素中心构造一组虚拟网格线，按直线从起点到终点的顺序计算直线与各垂直网格线的交点，然后确定该列像素中于此交点最近的像素[3]。

3）导引点优化

在地形相对平坦的环境下搜索路径点时，由于算法本身追求的路径最短或者代价最小，经常会出现路径紧贴障碍边缘的情况，如图4所示，蓝色区域表示障碍，非障碍区域内颜色越深表示行走代价越小，路径从障碍边缘经过。为了使搜索到的整条路径尽量平滑，应尽量保证与导引点相连的两段曲线在导引点处相切。如果导引点紧贴障碍边缘，会降低导引点处巡视器航向的选择范围。

图4 路径搜索结果Fig.4 Path search result

为了避免导引点紧贴障碍边缘，在搜索路径点时，可以将月面综合环境图中的障碍在原有尺寸的基础上进行附加膨胀。这样搜索得到路径点就不会出现紧贴原有尺寸障碍的情况。如图5所示，深蓝区域表示按照正常尺寸膨胀的障碍O1，淡蓝色区域为提取导引点时使用的障碍区域O2，按照O2区域搜索得到的路径点已经与O1区域保持了一定的距离。按照导引点提取流程将图5所示的路径点处理后，可以得到图6所示的路径导引点。

图5 障碍附加膨胀的路径点Fig.5 Path nodes of obstacle additional expansion

图6 障碍附加膨胀的导引点Fig.6 Guidance point of obstacle additional expansion

4）导引点航向的初步确定

巡视器在导引点处的航向很大程度上决定了整条路径的优化程度，但在提取导引点的过程中难以简单地确定航向。为了方便计算两个导引点间的路径，在导引点提取过程中，需要初步确定导引点处的航向。若设P点为从S(x0，y0)点到D(x1，y1)点的路径导引点，则P点航向角θ的初步计算方法为

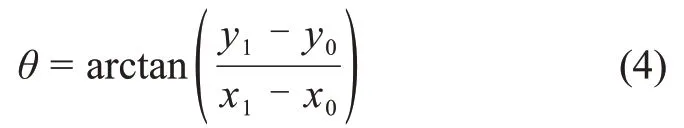
3.2 路径计算与拼接

路径导引点提取完成后，需要完成相邻两个导引点间的路径计算和与导引点相连两段路径的拼接。相邻两个导引点间的路径计算结果与巡视器在两导引点处的航向密切相关，而与导引点相连的前一段路径的终止航向和后一段路径的起始航向也直接决定了巡视器在该导引点上是否需要原地转弯，因此相邻导引点间的路径计算和导引点处的路径拼接需要同步考虑。

1）路径计算

相邻导引点间的路径可以采用基于试算法的预置曲线路径的方式来计算获得[4]，通过这种方法可以获得一个由不多于3段曲线组成的相对平滑路径集合，这个路径集合中的每一条路径都能够确保巡视器从前一个导引点安全行驶到后一个导引点。得到路径集合后需要对每一条路径进行代价的评估。

路径搜索在栅格化的月面综合代价图上进行，综合代价图上栅格的数值表示了巡视器通过该栅格需要付出的代价。行走代价Cs与路径经过的各栅格的综合代价值g相关，计算方法为

行走里程不同的路径，其代价也会不同，因此需要考虑路径的里程代价Cm。里程代价值的大小取决于路径的里程m和单位长度的代价值cpm，计算方法为

巡视器的移动控制期望更少地使用原地转向，因此在计算路径代价时，可以附加计算路径原地转向控制的代价Ct。原地转向代价与原地转向角度φ和单位角度的转向代价值cpt相关，计算方法为

巡视器移动路径的曲线段数越多，移动控制效率就会越低。因此需要考虑路径的控制代价Cc。控制代价取决于组成整段路径的单元个数n和每个路径单元的地面控制代价cpc，计算方法为

为了提高控制效率，应尽量避免得到的路径中包含里程较短的曲线，需要附加计算短里程曲线的路径单元里程代价Cum。假定仅当路径单元的里程mu小于d时，开始计算路径单元里程代价，并设μ为代价系数，计算方法为

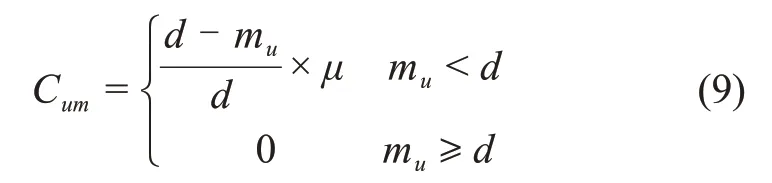
综合上述分析，路径综合代价Cg的计算方法为

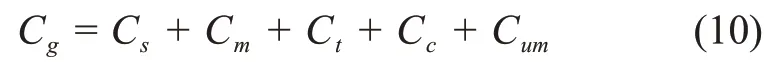
2）路径拼接

导引点处路径拼接与相邻导引点间的路径计算同步进行。路径拼接需要解决不同导引点间路径计算的顺序以及导引点航向调整两个问题。受到转弯半径限制，路径导引点之间距离越短，路径对起止点航向的适应调整能力越小。为了尽量保证路径的平滑性，多路径点的曲线拼接可以按照路径点间距离由小到大的顺序进行。相邻的两个导引点间路径计算完成后，若在导引点处存在原地转向且相邻的路径还未计算，则可以尝试调整导引点处的期望航向，尽量消除原地转向。

4 仿真实验结果

为了验证路径规划方法的合理性和有效性，分别对探测点可达性评估、多约束导航点搜索和平滑曲线路径搜索方法进行实验和分析。

图7的底图为经过适当比例缩小的真实月面影像，在探测周期规划过程中，点1为当前点，点7为探测点，经过多约束导航点搜索，得到了点2～6共5个导航点，各导航点设置较均匀，各导航点满足光照和通信要求。

图7 导航点搜索结果Fig.7 Search result of navigation points

对平滑曲线路径搜索方法特针对单一障碍地形和复杂障碍地形两种情况进行实验和分析，分析使用的图像为地面模拟巡视器在月背进行相机成像处理后得到的地形图。

图6所示的地形为模拟巡视器所处环境的正射投影图，并叠加了综合代价图，蓝色表示障碍。在获得如图6所示的路径导引点后，以点1为起点（航向90°），点3为目标点（航向60°），进行路径计算，得到了图8所示的曲线路径。路径由4段圆弧组成，无原地转向。

图9所示的路径为使用A*算法得到的路径点基础上提取得到导引点，并根据导引点信息计算的按直线加原地转弯方式行走的路径。通过分析图8和图9所示的两条路径可以发现，曲线路径的里程比直线路径略长，但曲线路径的控制次数更少，无须原地转向控制，具体数据见表1。总体来说，曲线路径控制效率更高，路径更优化。

图8 曲线路径Fig.8 Curve path

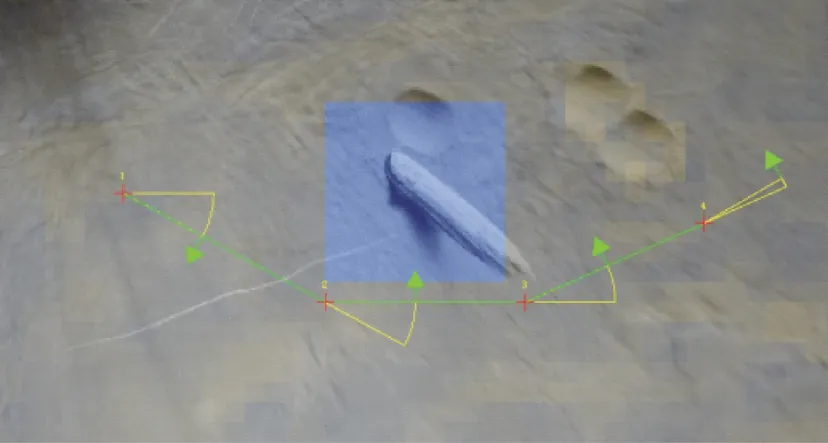
图9 按直线方式行走的路径Fig.9 Path of straight line walking

为了验证该方法在更复杂环境下的适应能力，模拟了图10所示的月面环境，A点为起点（航向90°），B点为目标点（航向60°）。图中显示的点为使用A*算法搜索得到的路径点。

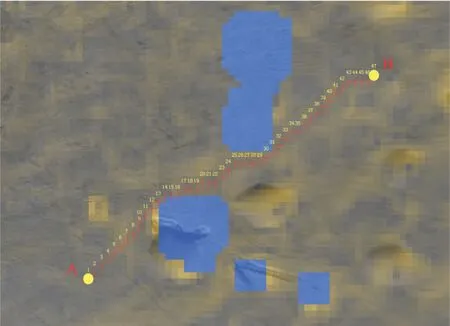
图10 A*算法得到的路径点Fig.10 Path nodes obtained by A*algorithm

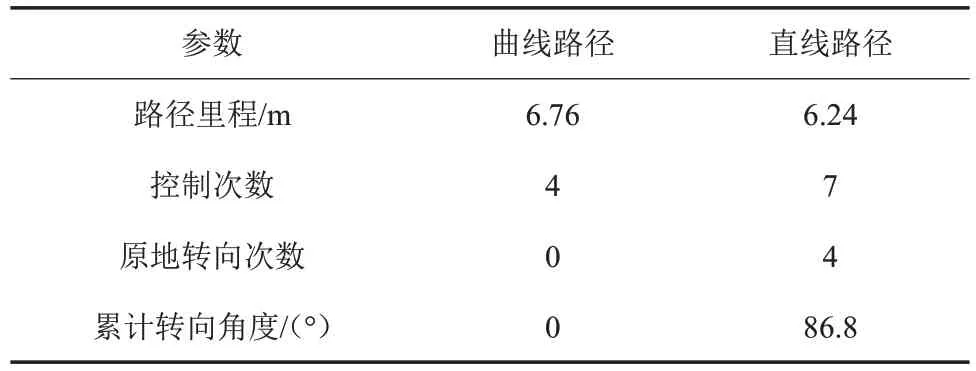
表1 单个障碍的路径搜索结果比较Table 1 Path search result comparison of single obstacle

通过对比图11所示的两条路径可以发现，曲线路径与直线路径的里程基本相当，曲线路径的控制次数更少，原地转向控制的累积转向角度更小，具体数据见表2。总体来说，曲线路径控制效率更高，路径更优化。

图11 复杂环境下的曲线和直线路径Fig.11 Curve and linear path under complex environment

表2 复杂环境下的路径搜索结果比较Table 2 Path search result comparison of complex environment

5 结 论

本文根据月面巡视器遥操作控制流程，提出了探测点可达性评估、多约束导航点搜索以及平滑曲线路径搜索方法。仿真结果表明，通过上述方法得到的规划结果可以提高控制效率，能够在不同规划层次上对遥操作规划提供技术支撑。