深空探测器可重构性评价与自主重构策略

徐赫屿，王大轶，刘成瑞，李文博，符方舟，张科备

（1.北京控制工程研究所，北京 100094；2.北京空间飞行器总体设计部，北京 100094）

引 言

近年来，深空探测受到各国学者的广泛关注。开展深空探测活动，是航天技术发展的必然选择，也是人类进一步了解宇宙、认识太阳系、探索地球与生命的起源和演化、获取更多科学认识的必需手段。由于深空探测飞行距离远、时间长、环境未知性较强，深空探测器必须具备自主导航与控制的能力[1-2]。要实现自主运行，需要针对深空探测过程中资源严重受限（包括计算资源、硬件资源以及能量资源）和不可维修的特点，开展深空探测自主故障处理的研究。

为了实现对深空探测器控制系统的自主故障处理，系统自身必须是可重构的。可重构性的定义为：在资源配置和运行条件一定的情况下，在保证安全的时间内，系统通过自主改变空间构型或控制算法等方式克服故障，恢复全部或部分既定功能的能力[3]。进行可重构性研究是提高深空探测器故障处理能力的根本所在。随着对深空探测器控制系统性能、可靠性和安全性的不断增长的需求，可重构性评价方法与自主重构策略设计引起了广泛的关注[4-6]。进行可重构性的理论研究、建立适用于航天器控制系统的可重构性综合评价与设计方法体系和实现深空探测器在轨故障处理的前移，对提升整个深空探测器的运行可靠性和在轨使用寿命、可维护性开辟了新的途径，具有较高研究价值和工程意义。

在可重构性评价方面，Moore等最早利用线性定常系统的能控性和能观性格莱姆矩阵对线性系统的可重构性进行评估[7]；针对非线性系统，Gehin等[8]利用伪逆法对系统的可重构性进行评估；除此之外，还有很多学者从组件角度出发，采用结构分解、功能分析等方法分析了系统可重构性[9-10]。然而，通过分析可知，现有成果存在一定的问题：没有综合考虑不同影响因素作用下，系统的可重构性定量评价，这将直接影响到评价结果的全面性，从而导致后续基于可重构性设计的控制器无法满足实际需求甚至失效的情况。

在自主重构策略设计方面，Qi等[11-12]针对无人机执行器故障，通过求解一组线性矩阵不等式（Linear Matrix Inequality，LMI），分析了自愈模块中参考模型的可达性并对参考模型重新设计，从而使故障系统达到重构目标；刘等[13]针对以单框架控制力矩陀螺为执行机构的航天器，分别设计了状态反馈控制器和反步法控制器，提出了分步设计控制律来实现欠驱动姿态控制。此外，大多数现有方法都没有在故障诊断模块和容错控制方案的设计阶段考虑时间延迟带来的影响。针对该问题，Liu等[14]和Dowell等[15]研究了故障诊断和重构控制的综合设计。然而，文献中的故障诊断模块和重构控制模块仍然是单独设计的。鉴于此，Casavola等[16]和Zhou等[17]提出了自愈控制的概念，其定义是：将故障诊断和重构控制方法纳入统一的框架，主动克服故障并使系统保持一定的控制性能。对照重构的定义可以看出，自愈控制是自主重构控制的一种有效途径，同时也是系统可重构能力的实现过程。Qi等[11]针对执行器卡死故障，提出了基于自愈控制的自主重构方法，保证了故障系统可以通过自愈控制恢复全部或部分功能。

综上所述，目前没有指标来检验这些重构策略的有效性等。除此之外，已有自愈控制未将观测误差考虑在内，这将极大地降低所设计控制器的实用性。本文给出了考虑系统能控性、跟踪性能和鲁棒性的可重构性综合评价指标，并基于所提出的可重构性综合评价指标，利用自愈控制的方法，进行自主重构策略的设计，实现了控制系统自主故障处理的目标。

1 深空探测器控制系统建模

深空探测器姿态运动学和动力学方程是研究评价方法和设计自主重构方案的基础。考虑如下航天器动力学方程[18]为

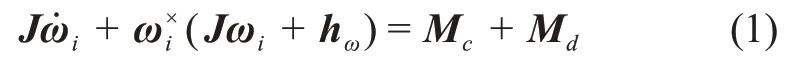
其中：J为深空探测器的惯量矩阵；ωi=[ωxωyωz]T为星体相对与惯性空间的角速度在星体坐标系中的投影矢量；hω为角动量；Mc为飞轮控制力矩；Md为各种干扰力矩总和；定义为

3-1-2转序下由欧拉角[φθψ]描述的运动学方程为

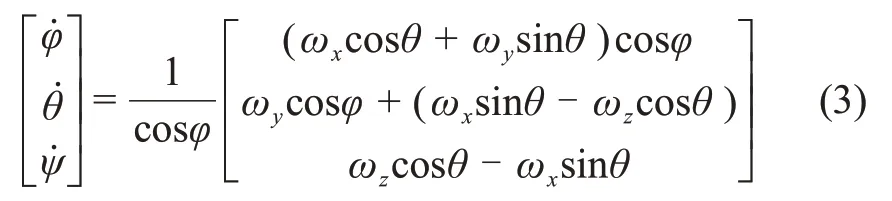
其中：ω=[ω1ω2ω3]T为深空探测器姿态相对轨道坐标系的转动角速度在星体坐标系下的投影。

ω与ωi大小满足的条件为

其中：Cob为轨道坐标系到星体坐标系的转换矩阵；ω0=[0ω00]T为轨道角速度。

其中：矩阵A为系统矩阵；矩阵B为系统控制矩阵；矩阵C为系统观测矩阵；x(t)为状态变量；u(t)为控制输入向量；y(t)为测量输出向量。

系统发生故障后，式(5)变为

其中：矩阵A、B、C分别为系统矩阵；Tu(t)、Tf(t)分别为系统执行器力矩和执行器故障；Td(t)系统干扰矩阵。

本文将针对式(5)和式(6)所描述的控制系统进行可重构性评价，并基于此给出合适的重构策略。

2 控制系统可重构性评价方法

控制系统的重构实际上是系统重构控制器在线重新设计的过程。在设计过程中，需要知道在哪些故障情况或部件失效的情况下能够通过自主重构达到目的。在设计系统重构控制器之前，首先需要对系统的控制可重构性进行分析与评价，定性或定量地判断系统是否具有可重构性或者可重构性能力的大小，从而为控制律重构设计提供理论依据。

2.1 考虑能控性的可重构性评价指标

控制可重构性本质上度量的是控制系统在不利条件下被控过程剩余的能控性。所以，需要研究故障系统的可重构性和剩余能控性之间的关系。

已有研究将控制系统基于能控性的可重构性指标定义为[7]

其中：Wc为系统能控性格莱姆矩阵；λmin(Wc)即为系统能控性矩阵的最小特征值。

由上述量化指标可以看出：可用ρc表征系统可重构性的大小，ρc越大，系统的可重构性越大，反之亦然。

在故障模式下，针对控制目标的重构控制问题，需要满足的条件为

其中：ρpth是预设的阈值，表示针对该重构目标所允许的最大边界。

假设控制矩阵表示为Bf(a)=[bf1a1bf2a2…bflal]T，则ρpth=maxρc，其中ρc满足如下条件

其中：Ω为控制变量的可行域。

式(9)给出了预设能量阈值ρpth的求取方法。该值与系统的输入变量、状态变量的约束有关。在阈值面ρpth之上的区域，均可通过重构控制，达到重构的目标。但若系统故障后，通过可重构性分析评价所得可重构性ρc不在阈值面ρpth之上的区域，则无法进行重构控制。该指标表征了系统剩余能控性[7]，可以从系统能控性的角度量化系统可重构性。

2.2 考虑系统跟踪性能的可重构性评价指标

系统良好的姿态机动性能和跟踪性能是深空探测器完成诸如在轨维修、空间观测等复杂任务的前提和保障。在重构设计时，需要检测原始参考是否可以渐近地实现。如果不能，将通过重构参考模型计算新的最佳参考。鉴于此，需要在可重构性评价中考虑系统的跟踪性能，从而实现故障情况下闭环稳定性和跟踪性能恢复的重构目标。定义如下考虑系统跟踪性能的可重构性指标

其中：δ代表系统干扰和系统故障；Δy代表受控输出的跟踪误差。

在故障模式下，针对考虑跟踪性能的重构控制问题，需要满足条件为

其中：Δy*为引起任务失败的最小受控输出的跟踪误差；ρtth表示针对考虑跟踪性能的可重构性指标阈值。

由式（11）可知，ρt的大小取决于系统的跟踪误差和干扰，该指标越小，意味着系统跟踪能力越强，原始参考能够渐进的实现，达到重构目标，因此该指标从跟踪性能的角度表征了系统的可重构能力。

2.3 考虑鲁棒性的可重构性评价指标

在重构控制系统中，需要同时做到：控制器具有鲁棒性、故障检测与诊断或参数辨识算法具有鲁棒性、重构的控制律具有鲁棒性。因此，鲁棒性也将作为衡量系统可重构性的一项度量指标。重构设计中，要求故障估计的误差对干扰是鲁棒的，即

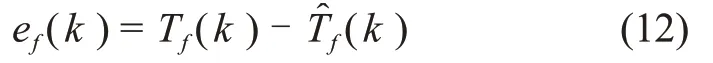
定义考虑系统鲁棒性的可重构性指标为

类似的，在故障模式下，针对考虑鲁棒性的重构控制问题，需要满足条件

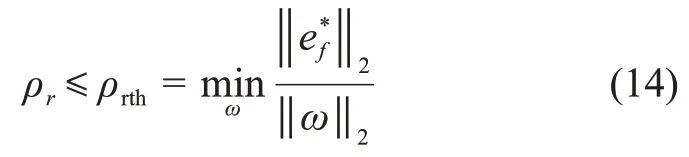
由式（14）可知，ρr的大小取决于系统的故障估计情况和干扰，该指标越小，意味着故障估计越准确，对干扰的鲁棒性越强，从对干扰的鲁棒性的角度表征了系统的可重构能力。

2.4 可重构性综合评价指标

控制重构的目标依原始控制器的目标而定，而单一的某一目标不足以描述所有问题，因此需要根据实际情况综合考虑不同的重构目标[19]。通过综合考虑系统的能控性、跟踪性能和鲁棒性，定义如式(15)所示可重构性综合评价指标。

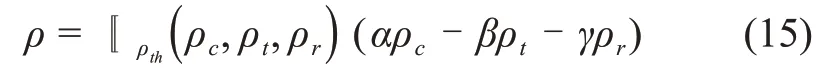
其中：α,β,γ分别为系统能控性、跟踪性能和鲁棒性在可重构性分析中的权重，通常由设计人员依据原始模型控制目标和实际任务需要选定；函数

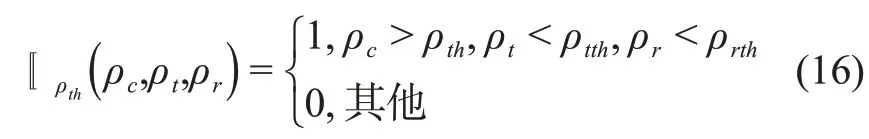
由ρc,ρt,ρr的定义可知，当该指标大于零时，表示系统是可重构的，且可重构性综合评价指标ρ越大，则系统可重构性越强。

本节给出了考虑到系统能控性、跟踪性能和鲁棒性的可重构性综合评价指标。该指标综合描述了系统的重构能力，为设计者在地面设计阶段对系统重构策略的设计提供必要的理论依据，实现深空探测器故障处理的前移，从而达到自主故障处理的目的。

3 深空探测器控制系统自主重构策略设计

本节将根据所得到的可重构性综合评价指标，给出基于自愈控制的系统自主重构设计方法。

3.1 自愈控制问题描述

模型参考方法用于设计系统(6)的跟踪控制器，参考模型为

其中：xr∈R6,Tur∈R3,yr∈R3分别是参考模型的状态、控制输入和输出向量。

参考系统的输出是所需的轨迹，给出如下参考模型的控制律

其中：Kx∈R3×6是保证系统稳定的状态反馈控制矩阵；Kr∈R3是保证参考模型中yr能够跟踪参考姿态r(k)的前馈控制矩阵。

令

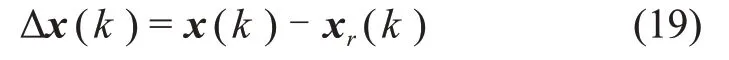
通过式(17)和离散化后的式(6)做差，得到误差动力学方程为

其中，

可以看出，通过设计合适的控制器ΔTu(k)可以使姿态误差渐近地收敛到零，从而跟踪上期望的姿态。

故障动力学模型和干扰可被描述为

其中：ΔTf(k)是两个连续时间间隔之间的故障模型的误差，Af=diag([Af1,Af2,Af3])表示自愈重构控制设计中的附加自由度；类似的，δTd(k)是2个连续时间间隔之间由于观测器干扰引起的误差，Afd=diag([Afd1,Afd2,Afd3])表示相应的附加自由度。令

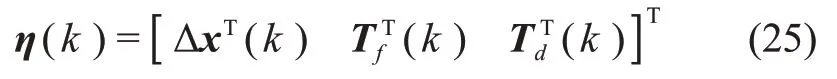
由式（20）～（22）和式（25）可得

其中：

根据系统(26)，提出的故障估计器/控制器为

针对上述自愈控制问题，已有文献给出了参数矩阵AF∈R9×9,BF∈R9×3,KF∈R3×9,DF∈R3×9,的具体算法，解决了自愈控制设计的问题。

3.2 基于可重构性评价指标的自主重构策略有效性判定

本节将基于第2节所得可重构性评价指标，利用上述自愈控制方法对系统自主重构策略进行进一步的设计。

文献[17]给出了自愈控制方法的适用条件，在此基础上，为了在设计阶段提高系统的重构能力，给出了综合考虑系统能控性、跟踪性能和鲁棒性的可重构性评价方法，具体结论如定理1所示。

定理1.考虑可重构性指标ρ>0，若存在正定矩阵X=XT∈R9×9,Y=YT∈R9×9,和矩阵使以下矩阵不等式成立，则式(27)描述的自主重构策略能够完成重构目标。

其中：M∈R9×9,N∈R9×9为式（34）的解。

该定理具体证明过程类似文献[17]，此处将不再展开。

根据定理1，给出基于可重构性评价指标的重自主构策略设计的流程：

步骤1：由于系统能控性是系统可重构的一个必要条件，所以首先分别计算考虑能控性、跟踪性能和鲁棒性的可重构性指标，判断是否满足自主重构条件；

步骤2：若满足，根据深空探测任务目标给出可重构性综合评价指标中的权重α,β和γ，求解可重构性综合评价指标，若不满足，则该系统不具有可重构性；

步骤3：设计控制器确定矩阵参数AF∈R9×9,BF∈R9×3,KF∈R3×9,DF∈R3×9,并通过式(30)～(33)得到矩阵具体形式为

步骤4：通过定理1和步骤3所得结果判断该自主重构策略是否有效。

4 仿真算例

考虑文献[21]中的深空探测器，具体参数如表1所示。

表1 深空探测器参数表Table 1 The parameter table of deep space detector

考虑如下扰动

其中：As表示扰动的幅度。

结合系统矩阵的定义，易得

当系统正常运行时，姿态角如图1所示。

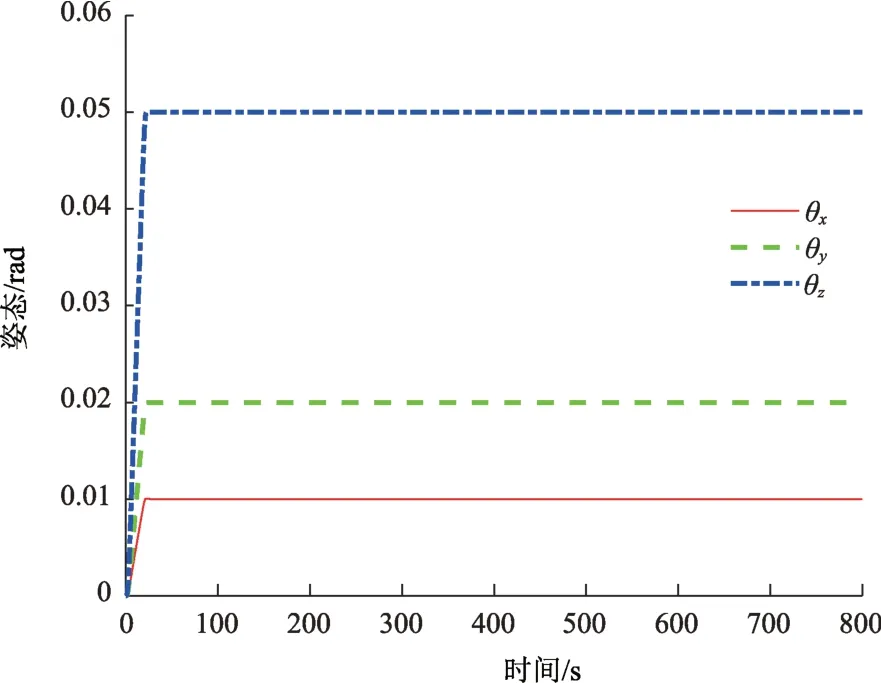
图1 无故障情况下的姿态角Fig.1 Attitude angle without fault

为不失一般性，设考虑系统能控性可重构性阈值、考虑跟踪性能可重构性阈值和考虑鲁棒性可重构性阈值分别为ρpth=0.79,ρtth=0.79,ρrth=0.79；故障矩阵和干扰矩阵分别为Af=0.99I3和Afd=0.1I3；系统故障力矩情况如图2所示，参考姿态为r(k)=[0.01 0.02 0.05]Trad，绘制系统发生故障时的可重构面如图3所示。

图2 故障情况Fig.2 Fault conditions

图3中横坐标分别表示执行机构a1,a2的故障情况，纵坐标表示该故障系统随着执行机构a1,a2故障的变化，可重构性的变化情况。在可重构面以上的区域，认为该系统故障后仍然保持能控性。根据式（7）计算所得系统基于能控性的可重构性指标ρc=0.95>ρpth，此时故障后的系统仍然具备足够的能控性。

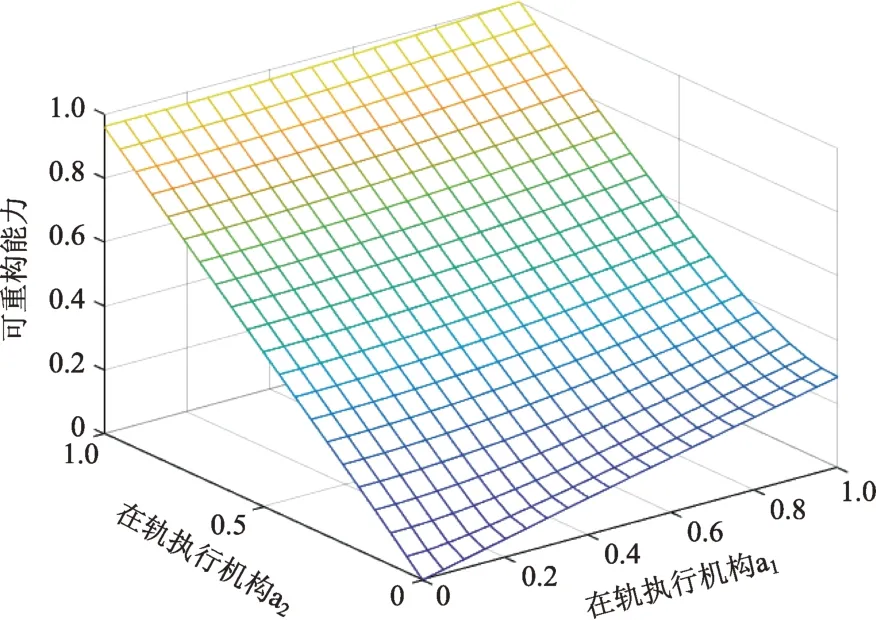
图3 考虑能控性的可重构性评价指标Fig.3 Results of reconfigurability evaluation index considering controllability

类似地，根据式（10）和式（13），可得系统基于跟踪性能和鲁棒性的可重构性评价指标分别为ρt=0.61<ρtth,ρr=0.52<ρrth，均满足自主重构条件。取权重α=0.5,β=0.25,γ=0.25，由式（15）计算其可重构性综合评价指标ρ=0.19>0，该系统具有可重构性。该指标综合描述了系统重构能力的大小，并在进一步自主重构设计中起到指导作用。

在自主重构设计中，所设计的故障估计器/控制器参数为

将参数矩阵AF∈R9×9,BF∈R9×3,KF∈R3×9,DF∈R3×9代入式（35）～（38）可得矩阵经验证，该组系数矩阵和可重构性指标ρ=0.19>0满足矩阵不等式（28）和式（29），根据定理1可知，该自主重构控制器可以达到重构目的。图4为故障后姿态角的情况，可以看出，即使在存在执行器故障和外部干扰的情况下，仍然以高精度遵循期望的姿态，达到重构目标，验证了定理1的正确性和有效性。

另考虑故障系统矩阵为=1.22I3；参考姿态为保持不变，此时可重构性指标ρc=0.65<ρpth，而可重构性综合指标ρ=0，即该故障无法进行自主重构。图5为故障后姿态角的情况，可以看出，此时系统不具备重构能力。

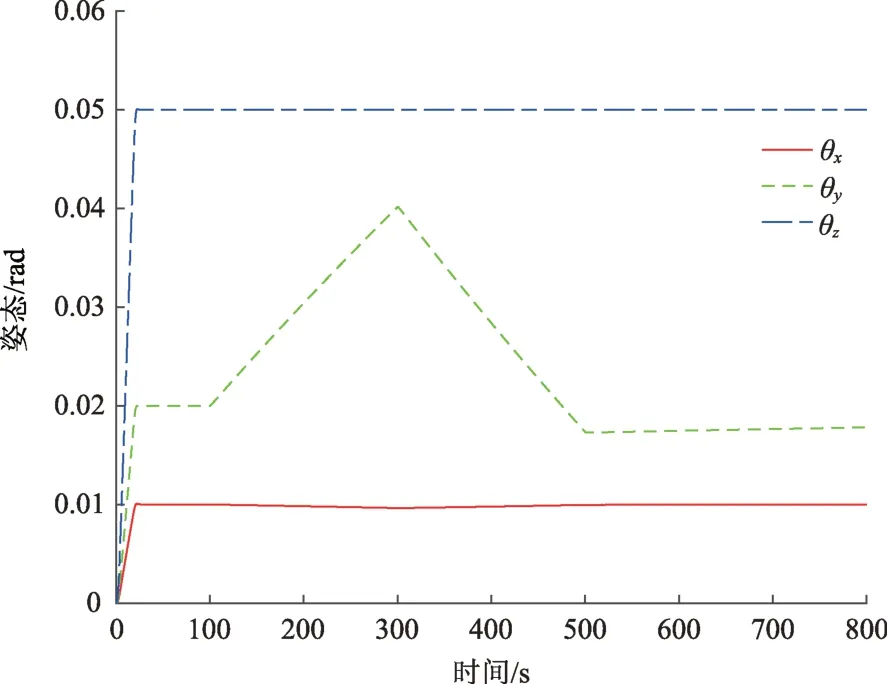
图4 故障矩阵为Af时的重构控制结果Fig.4 Reconfigurable control results with fault matrix Af

图5 故障矩阵为后重构控制结果Fig.5 Reconfigurable control results with fault matrix

5 结 论

本文阐述了深空探测器自主运行的必要性，通过综合考虑影响系统重构能力的因素，给出了可重构性综合评价方法。所得评价指标可以全面地描述系统的重构能力，为深空探测器自主重构策略设计提供必要的理论依据。由仿真结果可知，利用该指标对自主重构策略进行设计，可以有效地提升深空探测器在轨故障应对能力及自主控制能力，可确保探测器在轨运行阶段的安全性。