一种基于太阳自转轴观测角的新型天文导航方法

宁晓琳，晁 雯

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

引 言

天文导航是一种重要的深空探测导航技术，它具有全自主、抗干扰、误差不随时间积累等优点[1]。天文导航方法按量测量的不同可分为测角导航[2-5]、测距导航[6-8]、测速导航[9-10]3种。天文测角导航是目前应用最成熟的天文导航方法，已成功应用于“水手号”“旅行者号”“深空1号”“深度撞击号”等[2-5]深空探测器上，其不足是导航精度随探测器到目标天体之间距离的增加而降低。脉冲星测距导航是一种新兴的导航技术，其导航精度不受探测器位置的影响，但脉冲星发出的信号微弱，所需的观测时间较长，另外导航精度还会受到脉冲星星历误差、星载原子钟差、运动多普勒效应等的影响[6-8]。Liu等[7]提出一种新的脉冲星导航方法来抑制多普勒效应的影响。天文光谱测速导航可直接获得探测器的速度信息，但易受恒星自身光谱频率变化的影响[9-10]，针对这个问题，Ning等[10]提出一种差分多普勒辅助天文导航方法，但对于传感器测量噪声的影响需要进一步研究。现有的自主天文导航方法都存在局限性。因此，研究新型量测量及自主天文导航方法，为现有的天文导航方法提供补充是十分必要的。

太阳的观测和研究为人类探索天文导航方法提供了一种新的思路[11-12]。对太阳光谱进行频率鉴别诊断，可以提取太阳的有用信息。利用载有高光谱分辨率的空间外差光谱仪和原子鉴频仪的新型太阳敏感器观测太阳光谱波长的变化，可实现太阳光球层和色球层中物质运动速度场等信息的高精度测量，从而可获取太阳圆面不同位置处的速度差值[13]。中国科学院物理与数学研究所通过开展基于原子机制鉴频器的太阳观测，成功地获得了太阳全日面的多普勒速度观测结果[14]。通过光谱仪测量太阳圆盘面边缘上两组连线互相垂直点的速度差值，然后建立速度差值与太阳自转轴和太阳视方向的夹角的数学模型，可以解算出夹角θ。θ可以将探测器的位置确定于以θ为锥心角的圆锥面上，因此可把θ作为量测量来提供探测器的位置信息。

本文提出一种基于太阳自转轴观测角的新型天文导航方法。基于太阳探测器，通过建立速度差值与太阳自转轴观测角θ的数学模型，解算夹角θ并将其作为新方法的量测量建立量测模型。本文把太阳自转轴和太阳视方向的夹角θ统称为太阳自转轴观测角θ。仿真表明，新方法的导航精度较传统仅以太阳视方向r作为量测量的导航方法有所提升。同时，本文还对影响导航精度的测速敏感器精度、滤波周期和轨道倾角进行了详细分析。

1 太阳自转轴观测角θ的获取

利用新型太阳敏感器的4个光谱仪测量太阳圆盘边缘上两组连线互相垂直点的速度差值，利用中心轴线方向得到太阳视方向，根据太阳自转模型和投影原理，建立速度差值和太阳自转轴观测角θ的函数关系，从而解算出夹角θ，具体步骤如下。

1）测量新型太阳敏感器速度差值

新型太阳敏感器工作原理：太阳敏感器通过内置调节机构将4个光谱仪对准太阳圆盘边缘上两组互相垂直且连线穿越太阳圆心的点，4个光谱仪的中心轴线方向就是太阳视方向，两组点分别为A和A′，B和B′，根据多普勒频移原理，如图1所示，可测量分析得到A和A′、B和B′之间的速度差值dv1和dv2。

图1 新型太阳敏感器工作原理Fig.1 The working principle of Solar sensor

2）建立速度差值与θ的数学模型

太阳自转速率随纬度的变化而变化，其较差自转率[15]为

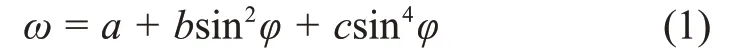
其中：ω是以°/日为单位的角速度；φ是太阳对应点纬度；a、b、c为常数，不同的测量结果会影响a、b、c这3个常数的值。

当前被接受的值：a=14.713°/日（±0.0491）、b=-2.396°/日(±0.188)、c=-1.787°/日(±0.253)。

作垂直于太阳视方向且经过太阳质心O的切面圆，即太阳圆盘面，在切面圆上任取一点M，沿子午线与赤道交于点N，设切面圆与太阳赤道的交点为起点S，顺时针为正，∠MOS=α，∠NOS=β，∠MON=φ，即M点的纬度为φ，建立空间直角坐标系O-xyz，如图2所示。

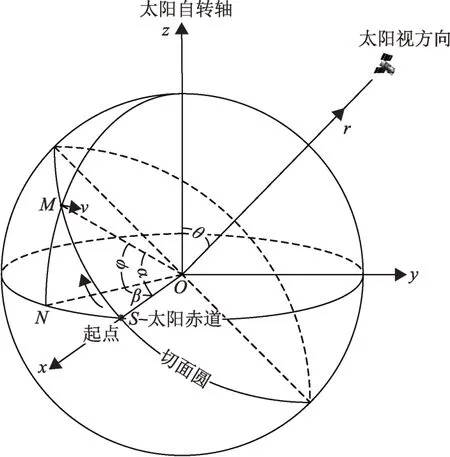
图2 空间直角坐标系Fig.2 The spatial rectangular coordinate system

由式（1）得切面圆上的点的自转线速率为

其中：太阳半径R=6.955×105km。

太阳视方向r=[0sinθcosθ]T，M点的速度v=[vsinβvcosβ0]T，则速度v在太阳视方向上的投影速度v1大小为

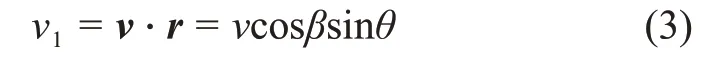
在球面直角△MSN中

由式（3）和式（4）得

则切面圆上相差180°的两点处的投影速度差dv为

在球面直角△MSN中

由式（2）、式（6）和式（7）得

3）解算太阳自转轴观测角θ

因为α∈(-π,π)，θ∈(0,π)，已知新型太阳敏感器测量数据为dv1、dv2，由式（8）可得方程组

将dv1、dv2代入式（9）便可解算出太阳自转轴观测角θ和π-θ，新型量测量θ的获取流程图如图3所示。

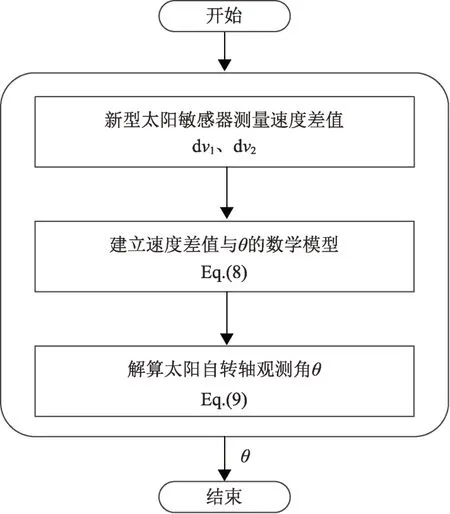
图3 量测量θ的获取流程图Fig.3 The flow chart of measurement acquisition

通过夹角θ可提供探测器相对太阳的位置信息，即探测器必位于以太阳为顶点，以θ为锥心角的圆锥面上，如图4所示。

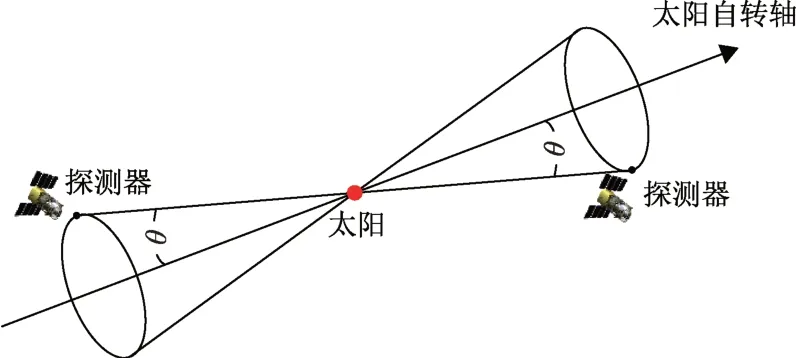
图4 探测器的位置信息Fig.4 The location of Solar explorer

2 以r或θ作为量测量的天文导航方法

2.1 量测模型

1）以r作为量测量的量测模型

太阳视方向是一种较易获取的传统量测量，以太阳视方向r作为量测量时的量测模型[18]为

其中：rps是探测器相对太阳的位置矢量；vr是量测噪声。

设Z1,k=r，量测噪声为V1,k=vr，则以太阳视方向为量测量的传统天文导航方法的量测方程为

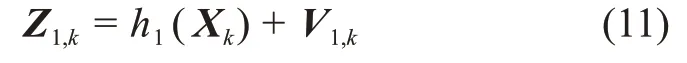
2）以θ作为量测量的量测模型

量测量θ可以提供探测器相对于太阳的位置信息，由此可以建立基于太阳自转轴观测角的新型天文导航方法的量测模型为

第三，党的十六大以来，以胡锦涛为总书记的党中央，在继承毛泽东思想、邓小平理论和“三个代表”重要思想的过程中，又进行了理论创新，提出了科学发展观和构建社会主义和谐社会的执政理念。与之相对应，也创新和发展了中国共产党的群众史观理论，提出了“以人为本”的群众利益观，中国共产党群众史观的践行进入到了一个新的发展阶段。

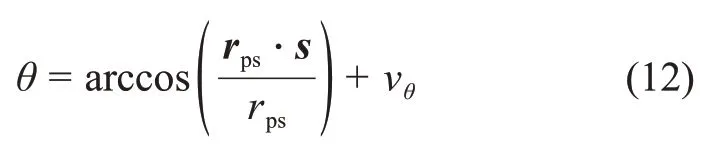
其中：s表示太阳质心坐标系下太阳自转轴的单位方向矢量；vθ是量测噪声大小。

设Z2,k=θ，量测噪声为V2,k=vθ，则以太阳自转轴观测角为量测量的新型天文导航方法的量测方程为

2.2 状态模型

太阳探测器的运动方程可以看作以太阳为中心天体的二体模型，在太阳质心坐标系下为

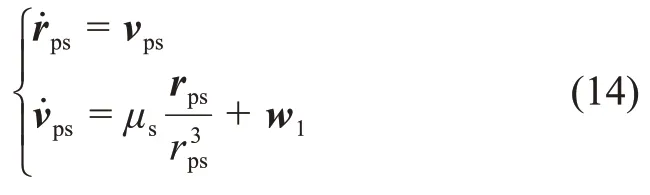
其中：vps是探测器相对太阳的速度矢量；μs是太阳的引力常数；w1是过程噪声。

3 仿真和分析

3.1 仿真条件

以太阳探测器为例进行仿真分析，图5为太阳探测器在太阳质心坐标系下的轨道图。仿真数据由STK（Systems Tool Kit）产生。其半长轴为1.07×107km，轨道倾角为60°，轨道偏心率为0°，升交点赤经为0°，近地点角距为0°。仿真时间为2个轨道周期，坐标系采用J2000.0 太阳质心坐标系。太阳敏感器精度为28″[17]，测速敏感器精度为1 m/s[18]，滤波周期为60 s。

图5 太阳探测器的轨道Fig.5 The orbit of Solar explorer

3.2 仿真结果

利用无迹卡尔曼滤波（Unscented Kalman Filter，UKF）方法对基于太阳自转轴观测角的新型天文导航方法进行了仿真分析，其中，量测量为太阳自转轴观测角θ。此外，本文还与仅使用太阳视方向r作为量测量的传统导航方法进行了比较。

3.2.1 两种量测量的导航结果比较

图6给出了以太阳自转轴观测角θ作为量测量和以太阳视方向r作为量测量的导航结果的对比图。表1给出了2 种方法在8 组不同的量测噪声下滤波收敛后的蒙特卡罗仿真平均结果，其中，以太阳自转轴观测角θ作为量测量的新方法采用均值为0，方差为1 的高斯白噪声，以太阳视方向r作为量测量的传统方法采用均值为0，方差为28 的高斯白噪声。仿真结果的统计时间段为仿真时间的2/3 时刻至结束。

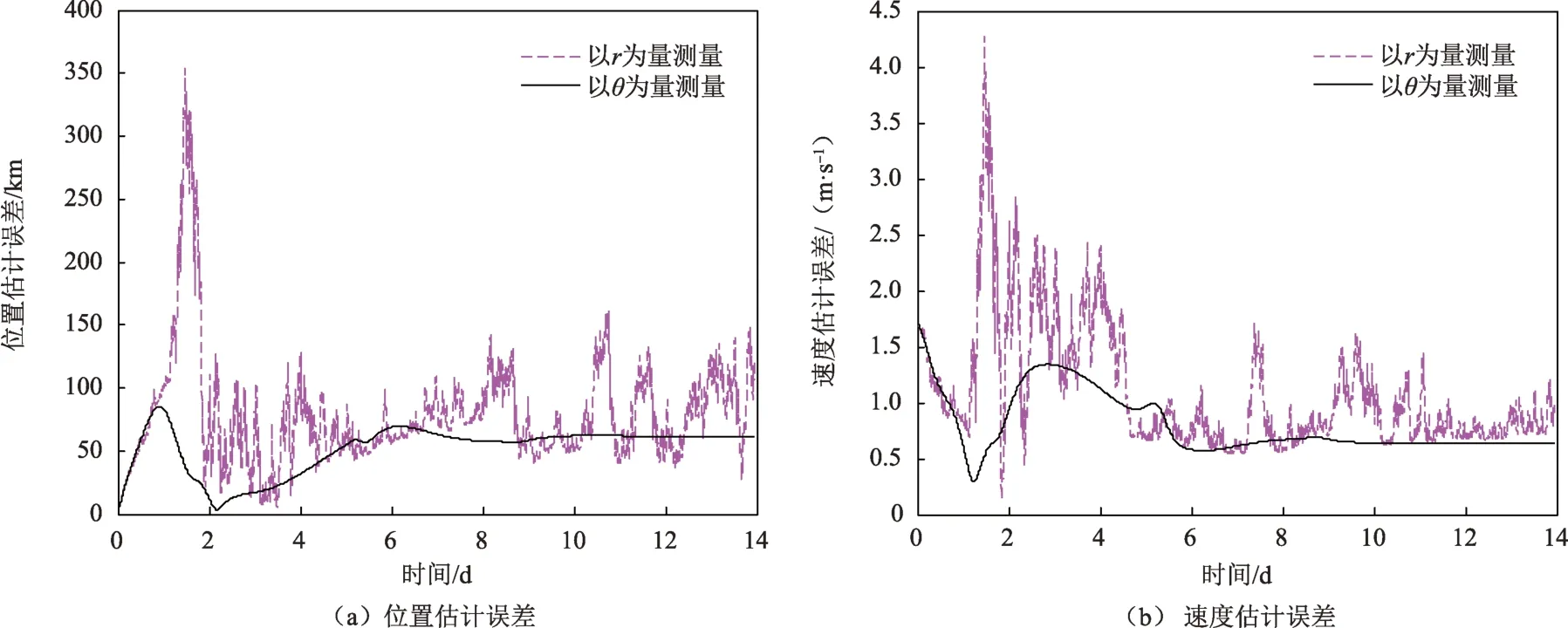
图6 两种量测量导航结果的对比图Fig.6 Comparison of two kinds of measurement navigation results

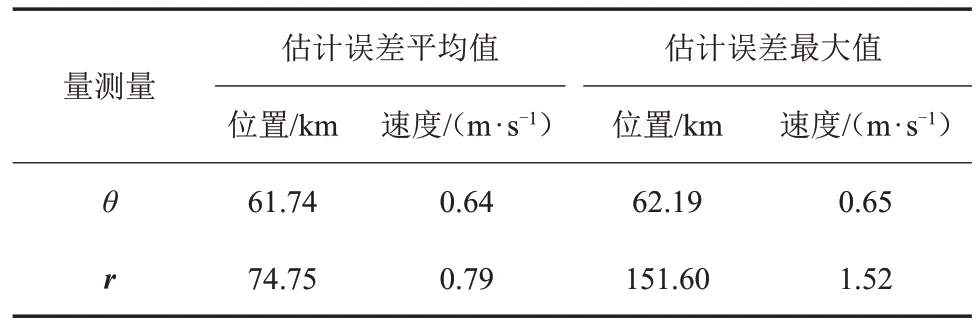
表1 两种量测量的导航结果Table1 Navigation results of two kinds of measurement

由图6可知：2 种方法均大约在仿真时间的1/3处开始收敛，以太阳视方向r作为量测量时曲线波动较大且收敛性较差，以太阳自转轴观测角θ作为量测量的新型导航方法曲线较为平缓且收敛性较好。由表1可知：所设的初始仿真条件下，相比较于以太阳视方向r作为量测量，以太阳自转轴观测角θ作为量测量的新型天文导航方法的导航精度提高了17.4%。

3.2.2 影响因素分析

本节对以太阳自转轴观测角θ作为量测量的新型天文导航方法的影响因素，包括测速敏感器精度、滤波周期和轨道倾角分别进行了分析。

1）测速敏感器精度对导航结果的影响

图7给出了只改变测速敏感器精度时的导航结果，仿真使用的轨道倾角为90°，其余仿真条件同3.1所述。表3统计了测速敏感器精度分别为0、1、10、100 m/s 时在8 组不同的量测噪声下滤波收敛后的蒙特卡罗仿真平均结果。由图7可知：测速敏感器精度对导航结果有影响，二者近似成线性关系。随着敏感器精度的提高，导航性能也在提升，但导航精度的提高是有限的。由表3可知：假定速度量测量获取时没有误差，位置速度估计误差也不为0，原因是仿真中状态模型即轨道动力学模型只考虑了太阳中心引力，将其他摄动项视为过程噪声，而由STK 生成的轨道模型采用高精度轨道预报模型（High Precision Orbit Propagator，HPOP），除太阳中心引力之外还考虑了其他的摄动，系统模型误差对导航结果的影响很大，在工程实现中要建立精确的系统模型。

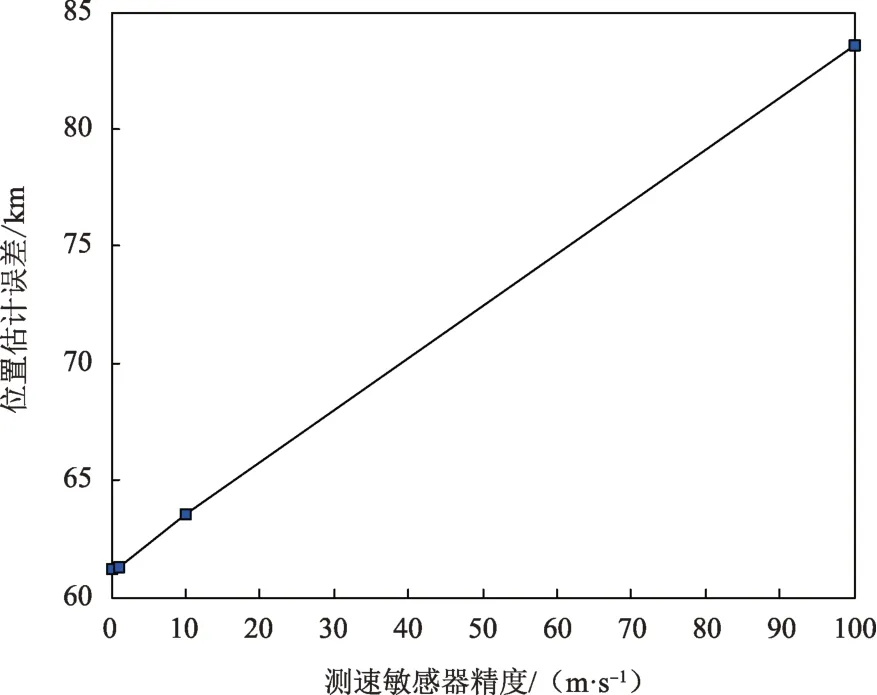
图7 测速敏感器精度对基于太阳自转轴观测角的新型天文导航方法的影响Fig.7 Impact of velocity sensor accuracy on the method using angle relative to solar rotation axis

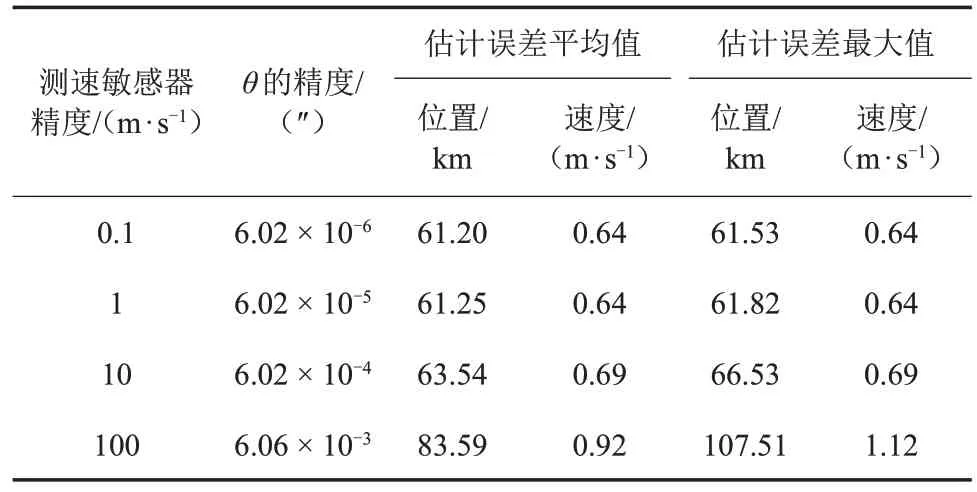
表3 测速敏感器精度对导航结果的影响Table 3 Estimation error of using different accuracy of velocity sensor

2）滤波周期对导航结果的影响

图8给出了只改变滤波周期时的导航结果。表4统计了滤波周期分别为60、600、1 200、1 800 s时在8组不同的量测噪声下滤波收敛后的蒙特卡罗仿真平均结果。由图8和表4可知，滤波周期对导航结果影响显著。滤波周期越长导航精度越差，且周期越长，位置误差增大速度越快。这是因为滤波周期越长，系统状态模型的线性化误差越大，导致系统导航精度降低。

3）轨道倾角对导航结果的影响

图9给出了轨道倾角分别为0°、30°、60°、90°时量测量θ的变化曲线。图10和表5给出了改变轨道倾角时在8组不同的量测噪声下滤波收敛后的蒙特卡罗仿真平均结果。由图9、图10和表5可知：轨道倾角对导航结果有影响。轨道倾角越大，位置估计误差越小。这是因为轨道倾角越大，量测量θ的变化范围越大，所提供的量测信息越多，导航结果越好。轨道倾角为0°时，由于量测量θ几乎没有变化，导航结果较差。

图8 滤波周期对基于太阳自转轴观测角的新型天文导航方法的影响Fig.8 Impact of filter period on the method using angle relative to solar rotation axis

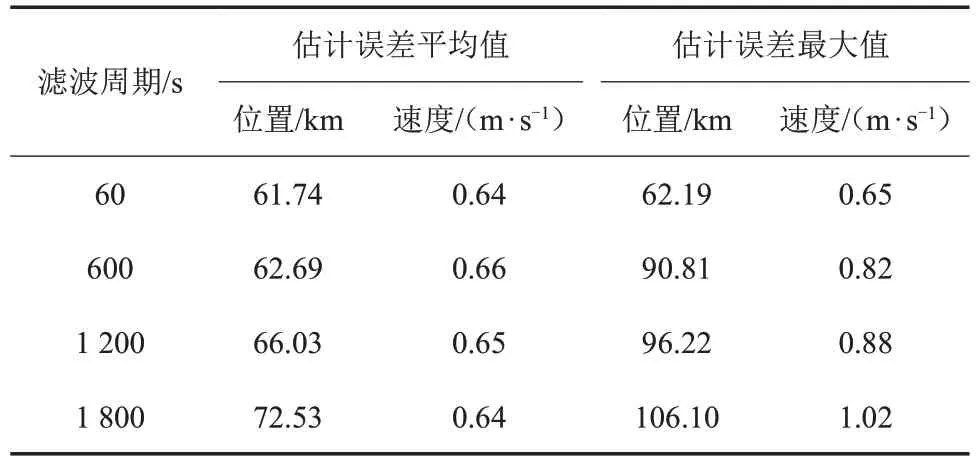
表4 滤波周期对导航结果的影响Table 4 Estimation error of using different filter period

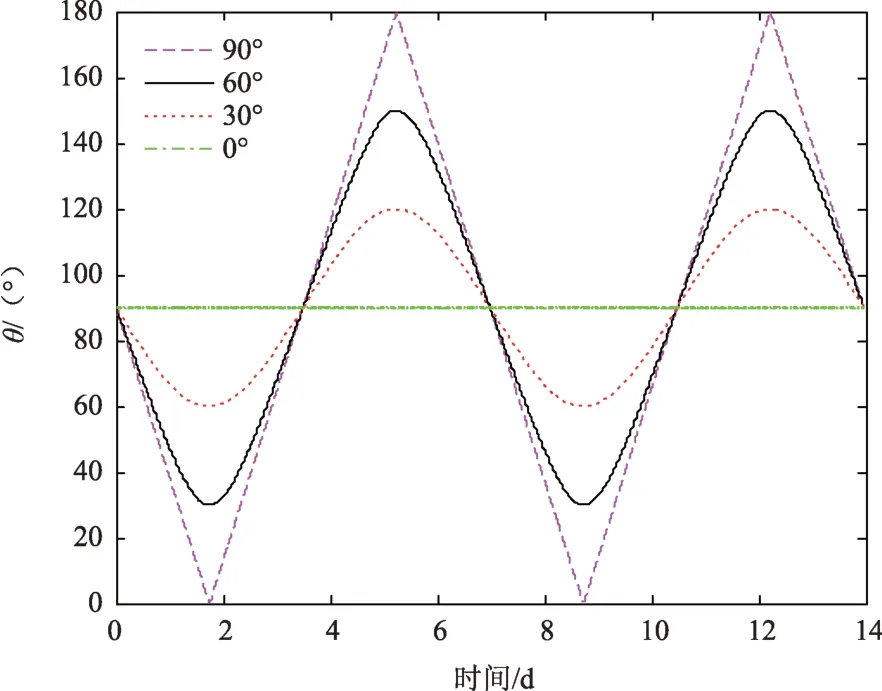
图9 不同轨道倾角时量测量θ的变化曲线Fig.9 Variation curve of θ in different orbit inclination

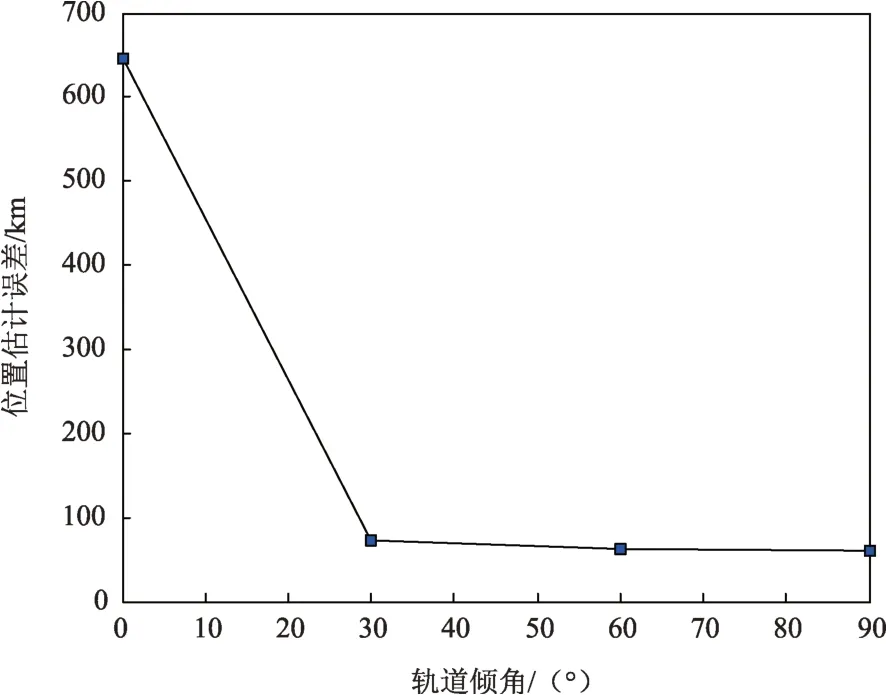
图10 轨道倾角对基于太阳自转轴观测角的新型天文导航方法的影响Fig.10 Impact of orbit inclination on the method using angle relative to Solar rotation axis

表5 轨道倾角对导航结果的影响Table 5 Estimation error of using different orbit inclination

4 结 论

本文主要介绍了基于太阳自转轴观测角的新型天文导航方法。首先介绍了新型量测量的获取方法，通过光谱仪测量太阳圆盘面边缘上两组连线互相垂直点的速度差值，建立速度差值与太阳自转轴观测角θ的数学模型，解算夹角θ并将其作为新方法的量测量来提供探测器的位置信息，然后建立了新方法的量测模型和状态模型。

利用太阳探测器对基于太阳自转轴观测角的新型天文导航方法进行了仿真校验，仿真结果表明相比较于传统仅以太阳视方向r作为量测量，以太阳自转轴观测角θ作为量测量的新型天文导航方法的导航精度提高了17.4%。为深空探测自主导航提供了新的理论与方法，下一步研究工作：太阳光谱的不稳定性对该方法性能造成的影响；光谱仪测量详细过程以及全链条的工程实现性和误差影响分析。