X射线脉冲星动态信号处理方法研究

张大鹏，李治泽，王奕迪，郑 伟

（1.国防科技大学空天科学学院，长沙 410073；2.中国西安卫星测控中心，西安 710043）

引 言

X射线脉冲星导航是一种新兴的航天器自主导航方法。相对于传统的天文导航方法，该导航方法可获得位置、姿态、参考时间等完整的导航信息[1]；相对于地基无线电导航，该方法可使航天器摆脱对地面测站的依赖，避免信号传播时延；相对于人造导航卫星，X射线脉冲星的运行特性不会受到人为干扰，其导航适用范围也不受近地空间限制[2]。

脉冲星导航的数据处理部分大致包括3个方面的内容：脉冲星信号周期搜索[3-5]、脉冲星信号降噪[6]、脉冲到达时间估计[7-9]。目前，大部分研究的方法均仅适用于已知探测器精确位置或假设探测器在惯性空间中静止的情况。

经过40 余年的发展，脉冲星导航技术已经实现了在轨空间验证，相信在不久的未来将实现工程应用。在实际导航中，航天器精确位置信息未知，根据航天器在轨动态接收的单光子信号解算脉冲星导航测量值是脉冲星导航中的重点，也是实现X射线脉冲星导航的基础[10]。

X射线脉冲星信号流量极弱，难以在短时间累积出脉冲轮廓，导致X 射线脉冲到达时间求解的特殊性[11]，即航天器必须持续观测X射线脉冲星一段时间（通常是千秒量级）累积足够多的光子，才能从接收到的光子到达时间（Time of Arrival，ToA）序列中提取出脉冲ToA[12]。

当航天器处于静止或匀速直线运动状态时，光子ToA序列的Doppler频率为常值，估计该常值Doppler频率的方法较为成熟。但是航天器在空间中相对惯性系做轨道运动，航天器所接收到的脉冲星信号频率因多普勒效应而连续变化[13]，这种动态的变化使得脉冲的信号处理难度较大。在脉冲星的观测时间内，航天器的位置信息通常通过轨道动力学模型外推得到[14-15]。轨道动力学模型的外推不可避免地会将轨道初始误差和随机误差引入脉冲到达时间的计算中，并最终影响X射线脉冲星导航的精度。因此，研究动态信号的处理方法是解决脉冲星导航实际应用问题必须突破的关键技术。

1 动态信号处理原理

1.1 导航基本原理

基于X射线脉冲星导航的航天器定位是通过比较航天器与SSB（Solar System Barycentre）处的脉冲星信号相位差来提取导航观测量的。这些观测量反映的是SSB 到航天器的矢量在脉冲星视线上的投影。通过处理一个或多个不同方位的脉冲星测量结果并结合轨道动力学进行滤波，便可以得到航天器位置速度的最佳估计值，该原理的如图1所示。

图1 X射线脉冲星导航原理Fig.1 Principle of X-ray pulsar-based navigation

1.2 动态信号处理原理及步骤

为了提出适用范围广的脉冲星动态信号处理方法，引入轨道动力学的辅助。预估轨道是航天器上的脉冲星导航系统结合轨道动力学等其他可获得的导航信息综合外推估算的航天器轨道值，含有一定的误差。动态信号处理的目的即通过比较P点（航天器所在位置）和SSB点的脉冲星相位轮廓相位的变化，估算航天器导航测量位置信息。航天器脉冲星导航观测值解算原理，如图2所示。

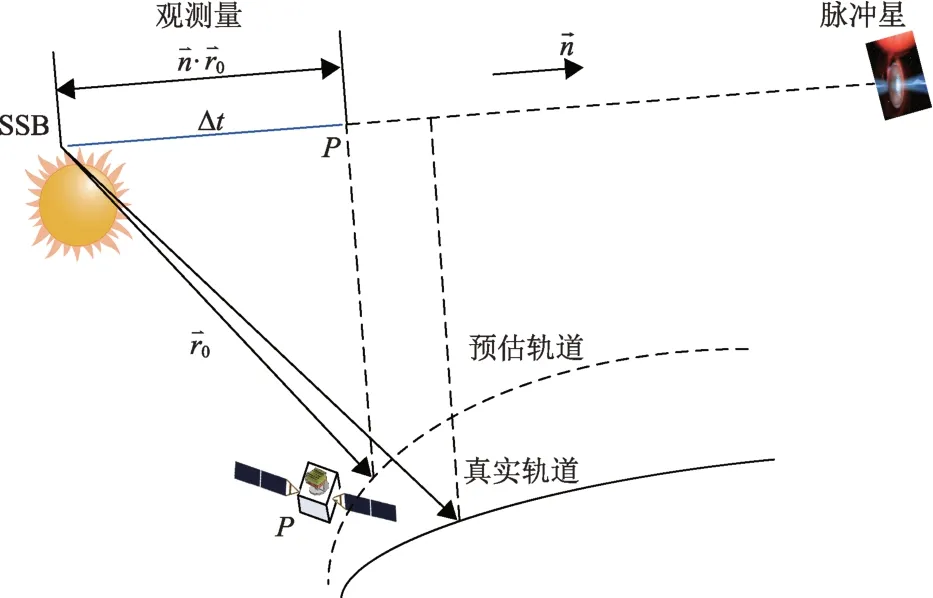
图2 脉冲星导航观测量提取原理Fig.2 Principle of extracting navigation observation of pulsar

动态信号处理主要步骤：①光子时间转换，根据预估轨道信息，将观测周期内的所有光子到达时间折算到P点；②航天器处信号轮廓折叠，估计相位误差吸收项系数，并折叠指定时刻P点信号轮廓；③SSB处信号预测，根据SSB点计时模型和对应脉冲星信号模板，推算指定时刻SSB 点的信号；④比较P点和SSB点信号轮廓，估计两者相位差，最终求得导航观测量。

2 动态信号处理过程

2.1 光子时间转换

X 射线探测器接收到的脉冲星信号是它在轨道不同位置处接收到的。为解算某一指定时刻航天器探测脉冲星信号轮廓，需要将航天器探测的所有光子到达时间都折算到这一时刻航天器所在位置处。这一步时间转换可消除光子到达时间中因航天器在轨道运动造成的时间偏移。消除轨道动态的光子到达时间为

其中：tSC是航天器接收到的光子到达时间；是脉冲星方向矢量；是航天器位置矢量（从SSB点指向航天器 X 射线探测装置中心）；是P点处航天位置矢量，c表示真空光速。

需要说明的是，在动态信号处理中，代入的是预估轨道信息。因此，预估轨道与真实轨道之间存在的误差会导致轨道动态不能被完全消除，产生的时延会导致相位传播误差，需要进一步估算。

2.2 航天器处信号轮廓折叠

折叠航天器P处的信号轮廓需要计算所有该点光子到达时间所在的相位。严格来说航天器处的时间相位模型是未知的，但在误差允许范围内，可以利用SSB处的时间相位模型外推获得。

根据脉冲星信号相位传播模型，SSB处的脉冲星信号相位可表达为

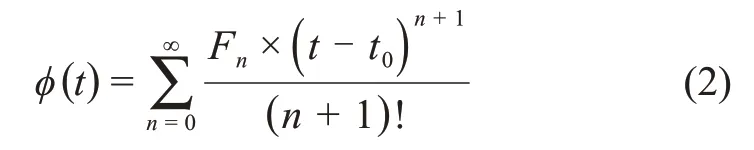
其中：t0是星历表历元，此时信号相位为零；Fn是脉冲星星历表计时参数，表示t0时刻脉冲星信号自转频率及其高阶导数。

若tSC0时刻航天器在P处，于是P处的时间相位模型可推算为

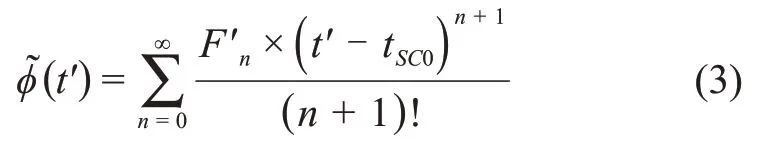
当需要折叠航天器处信号轮廓时，必须要先推算tSC0时刻航天器P处的脉冲星星历表。若仅考虑不大于2阶的脉冲星自转参数，星历表计时参数可外推计算如下

其中：ΔT=tSC0-t0-Δt。

虽然在实际场景中航天器与SSB之间的光行时差Δt不精确已知，但它可通过预估轨道信息进行粗略的估算。

此外，在地球低轨航天器导航应用模式下，由于导航脉冲星自转参数很稳定，在Δt时间内变化很小。在Δt不精确的情况下，外推星历参数通常仍然是可靠的。

以自转参数变化相对较大的年轻脉冲星Crab为例，说明在Δt不精确已知的情况下，外推航天器处星历表参数的可行性。

Crab自转频率一阶导数F1约等于-3.68×10-10Hz/s，自转频率二阶导数F2在10-19Hz/s2以下。当预估轨道误差分别为 1 0000、1 000、100 km 时（x，y，z三向，等权重），式（4）参数对光子相位计算的影响如图3所示。

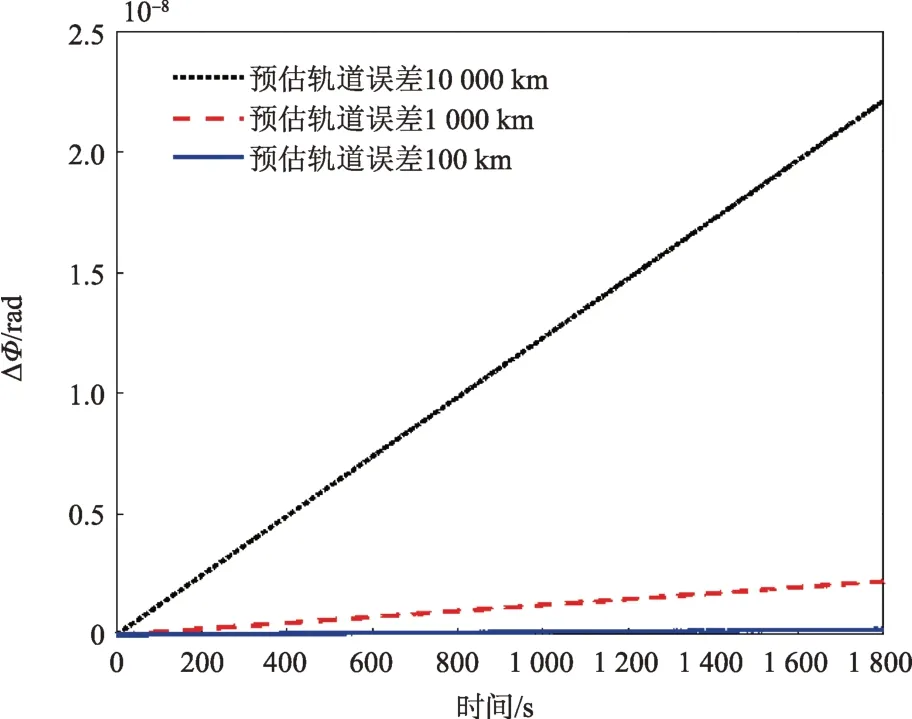
图3 预估轨道误差对光子相位计算的影响Fig.3 The effect of estimated orbital error on calculating the photon phase

因此，若预估轨道误差小于1 万km，在折叠轮廓Bin数小于107（即每个轮廓点的相位宽度10-7）的情况下，按照以上方法外推的计时参数都不会对折叠轮廓产生影响。对于Crab 脉冲星，此时折叠的脉冲星信号轮廓时间精度优于5 ns，这已经完全满足了实际导航任务的需要。

前文已经说明，在将光子到达时间折算到航天器处时，使用的是含有误差的预估轨道信息⇀pre。所以，式（1）处理得到的t′（这里记为tpre）并没有完全消除轨道动态，进而导致式（3）的外推相位存在误差。这部分误差需要利用参数估计方法来处理。若预估轨道误差导致的光子位置转换误差为te，则式（3）进一步改写为

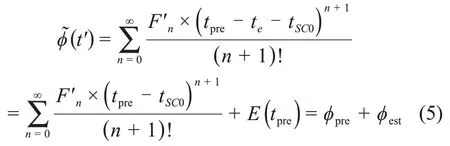
2.3 相位误差估计

tSC0时刻SSB处的信号相位可由公式（2）预测。而脉冲星信号零相位模板由脉冲星数据库获得，可以得到tSC0时刻SSB处的脉冲星信号轮廓。

经过以上步骤处理以后，动态信号处理问题被转化为相位误差的估计问题。只要能准确估计相位误差模型中的待估系数，就可以处理得到更准确的航天器处脉冲星信号轮廓。相位估计大致可分为基于历元折叠方法和极大似然直接估计2种。极大似然直接估计的方法适用于光子数量较少的情况，若光子量过大算法估计时间会较慢。本文处理的实测数据来自于Crab脉冲星观测，Crab脉冲星是空间的强X射线源，光子量较大。因此，本文采用基于历元折叠的相位估计方法。

1）参数搜索指标函数

由于预估轨道存在误差，导致光子到达P处的转换时间存在误差，进而导致光子相位计算不准确，这将影响脉冲星信号轮廓的峰高度。通过待估系数搜索，搜索使信号轮廓最突出的参数，充分吸收预估轨道导致的光子相位误差。因此，参数搜索的指标函数可以表示为

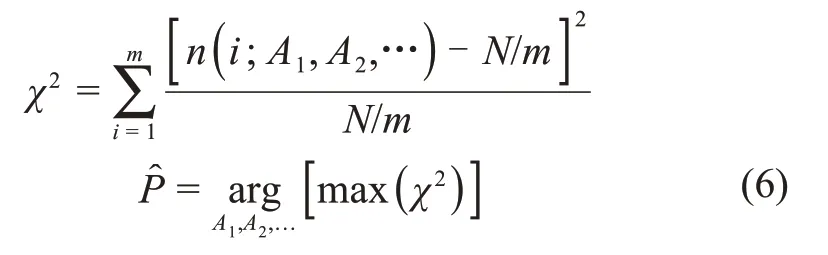
其中：m是折叠轮廓选择的Bin 数，总光子量N=是第i个Bin中的光子数目。在进行参数Ai估计过程中需要使用到全局优化算法，如全局搜索方法、遗传算法、退火算法等。

2）指标函数拟合

在实测数据处理中，计算的χ2存在一定毛刺影响参数估计精度。因此，在寻优之后还需要对获得的χ2值进行拟合处理，从而得到更接近真实的指标峰值点。本文采用傅里叶函数进行拟合为

其中：a0、ai、bi是拟合系数。

3）相位差估计

相位差估计是比较航天器处轮廓和SSB处轮廓的相位差，可利用互相关估计器。

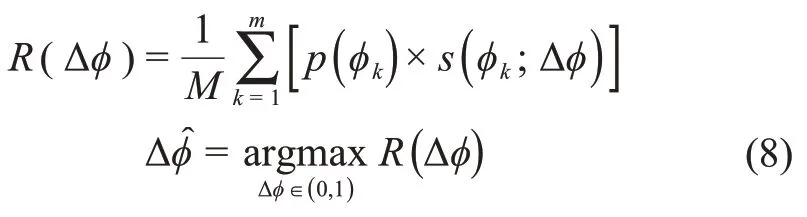
其中：p(φ)为脉冲轮廓；s(φ)为标准轮廓；R(Δφ)为相关函数；m为两组信号轮廓数据的Bin数。

最后导航观测量为

其中：Δφ是比较轮廓得到的相位差；N是整周期部分，可以用预估位置r估算。

3 卫星实测数据动态信号处理实验

3.1 HXMT卫星实测数据处理

硬X射线调制望远镜“慧眼”（Hard X-ray Modulation Telescope，HXMT）是中国科学院研制的X 射线辐射源天文观测卫星，它工作在大约550 km 高度的正圆轨道，轨道倾角约43°。

所用数据为 2017年9月1日—2017年9月5日时间范围内的Crab 脉冲星观测数据，观测探测器为He高能探测器。采用的预估轨道根数如表1所示，它是脉冲星导航实验24天以前所确定的轨道根数。

将全部的光子到达时间观测数据按1 800 s 的时间长度分成数据包，在去掉光子量不足的数据包后，共有143组。利用预估轨道信息将光子折叠到每包数据的首光子到达时刻的航天器位置处。为了减小计算量，时间相位模型仅考虑不大于一阶的自转参数，即

表1 预估轨道根数Table1 The estimated orbit element values of HXMT

对参数A1进行全局搜索，指标搜索（蓝实线）和指标函数拟合（红虚线）的结果如图4所示。实验表明，与直接采用搜索得到的参数相比指标函数拟合方法可使导航观测量解算精度提高近1 倍。

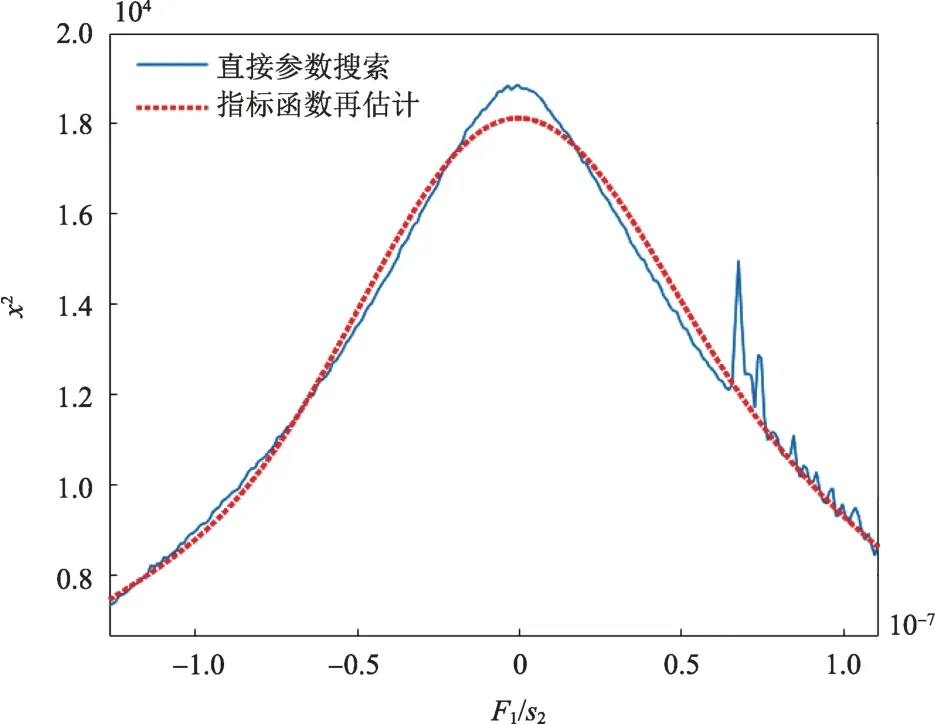
图4 参数搜索指标函数Fig.4 Indicator function of searching parameter

动态信号处理结果与卫星搭载的GPS 接收机定位数据进行比较。动态信号处理得到的观测量精度如图5所示。其中，误差标准差为41.1 μs，误差均值为-14.1 μs。

通过动态信号处理有效提高了导航观测量解算精度。与预估轨道外推位置所对应的观测量相比，导航观测量误差标准差减小了26%，误差均值减小了71%。

3.2 XPNAV-1卫星实测数据处理

XPNAV-1 卫星工作在轨道高度约500 km 的近圆轨道，轨道倾角约97°，属于太阳同步轨道卫星。

所用数据为 2017年9月10日-2017年9月12日时间范围内的Crab 脉冲星观测数据，观测探测器为掠入射探测器。采用的预估轨道根数如表2所示，它是脉冲星导航实验14天以前所确定的轨道根数。

图5 动态信号处理结果Fig.5 HXMT observation error of dynamic data processing

表2 预估轨道根数Table2 The estimated orbit element values of XPNAV-1

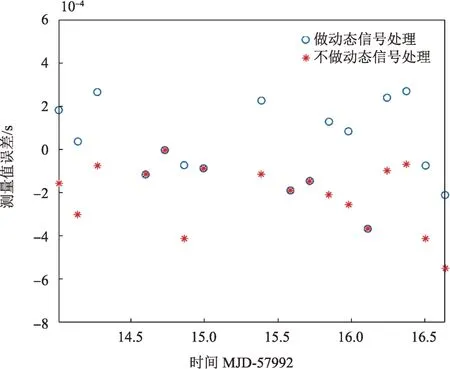
图6 动态信号处理结果Fig.6 XPNAV-1 observation error of dynamic data processing

与处理HXMT 卫星数据一样，时间相位模型仅考虑不大于一阶的自转参数。将全部观测数据按3 000 s 时间长度分成数据包，共有17 组。动态信号处理结果与卫星GPS 定位数据进行比较，数据处理结果情况如图6所示，导航观测量误差标准差为119.6 μs，均值为9.5 μs。而不做动态信号处理，按预估轨道进行外推，误差标准差为151.4 μs，均值为-209.9 μs。

从图6对比中可以看出，预估轨道外推位置所对应的观测量误差均值较大。通过动态信号处理有效校正了预估轨道误差所造成的光子相位计算偏差，大幅提高了测量值解算精度。

4 结 论

为提高脉冲星在轨数据处理精度、满足脉冲星导航工程应用需求，本文研究并提出了一种适用于低轨高动态情况的X射线脉冲星动态信号处理方法。该方法利用多项式吸收因预估轨道误差导致的光子到达时间相位误差，并针对实测数据信噪比偏低的问题采用了指标函数拟合处理，进一步提高了数据处理精度。实验验证结果表明，对于HXMT 卫星实测数据，利用轨道根数外推24 天的预估轨道信息，动态信号处理算法使导航观测量精度提高了71%。对于XPNAV-1卫星实测数据，利用轨道根数外推14天的预估轨道信息，本文采用的动态信号处理算法也大幅提高了导航观测量解算精度。