基于双目视觉的非合作目标自主姿态估计方法

胡启阳，王大轶

（1.北京控制工程研究所，北京 100190；2.北京空间飞行器总体设计部，北京 100094）

引 言

自主在轨服务是指通过空间智能服务航天器来实现为运行中的航天器在轨加注、在轨维护等空间任务。开展在轨服务可以延长卫星使用寿命，减少卫星运营成本，对于航天事业的可持续发展具有重要的实际意义[1-3]。利用相对导航实时获取目标相对于服务航天器的相对位姿信息，是开展在轨服务操作的必要前提。而在轨服务的对象如失效卫星等，一般属于“非合作目标”，具体表现：①未安装用于辅助测量的标识；②无法通过星间链路向外传输自身信息；③处于失控的自由运动状态。因此，和以往的交会对接任务相比，对象的上述非合作特性给面向在轨服务的相对导航任务带来了全新的挑战[4-5]。

目前，非合作目标相对导航主要依靠光学测量的手段，即通过服务航天器上安装的光学敏感器对目标进行观测来实现相对位姿的估计。国内外学者对相对导航算法进行了广泛的研究，取得了不错的成果。基于主动光学敏感器的导航研究方面，Li等[6]研究了卡尔曼滤波与迭代最近点相结合的估计方法。Mishra[7]针对各种导航滤波器结构及其可观性进行了分析。Mahboubeh等[8]研究了基于点云观测的多信息融合估计方法。

和激光雷达等主动测量方案相比，以单/双目视觉为代表的被动光学敏感器不仅测量分辨率较高，而且能够进一步获得目标表面的特征，同时具有重量轻、功耗低等优点，是近距离相对导航更为理想的观测手段。Segal等[9-10]建立了目标表面特征点的姿轨耦合运动模型，并通过双目相机观测特征点估计相对位姿和主轴惯量比。Qian等[11]结合双目视觉测量，利用最小二乘与凸优化方法估计位姿。文献[12]提出了基于对偶四元素的姿轨一体化估计方法。Hou等[13-14]研究了基于松耦合的相对导航方法，并对不同的滤波算法进行了比较。

目前针对空间非合作目标的相对导航方法均假定目标处于翻滚状态。事实上，当考虑空间干扰力矩的长时间作用，以及目标挠性结构及液体晃动的影响，航天器的运动存在着能量耗散。根据稳定性理论，随着时间的推移，目标会从最初的失控翻滚状态逐渐变为绕其自身最大惯性主轴方向自旋。因此，有必要针对处于自旋运动状态的非合作目标的姿态估计问题开展研究。

Markley变量是一组基于角动量的姿态表征方法，在描述自旋运动时变化相对缓慢并且精度较高，适用于自旋卫星的姿态估计问题[15-17]。然而，目前Markley变量均用于描述卫星自身的姿态，还未曾用于相对导航过程中对于目标的姿态观测问题。本文提出基于双目视觉的非合作目标姿态估计方法，利用Markley变量对目标进行描述，并通过双目相机观测目标表面特征点以实现目标自旋角速度与自旋轴方向的估计。

1 系统动力学及观测模型建立

1.1 建立坐标系

相对导航的测量和估计过程涉及到不同坐标系之间的相对运动，为便于后续描述，引入如下坐标系。

地球惯性坐标系{I}：原点为地心；x轴指向春分点；z轴指向地球北极；y轴的确定满足右手正交系。

双目相机坐标系{C}：原点为左相机的投影原点OC；x、y轴方向平行于成像平面并正交；z轴沿左相机的光轴垂直于成像平面。

目标航天器本体坐标系{T}：原点为目标航天器的质心OT；坐标轴方向平行于惯性主轴方向，其中，z轴为最大主轴方向。

1.2 基于Markley变量的动力学模型

Markley变量是一种基于角动量的航天器姿态运动表征方法，由LI、LB和ζ组成。LI和LB分别是目标航天器相对于其质心的角动量在惯性系以及本体系下的展开形式，并满足模长相等的约束|LB|=|LB|=L。二者的动力学方程分别为

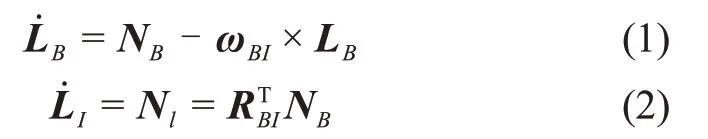
其中：NI和NB分别是合外力矩在惯性系与本体系下的分量；ωBI是航天器相对惯性系的角速度在本体系下的分量；RBI表示由惯性系到航天器本体系下的方向余弦矩阵。

当假定航天器为刚体时满足

其中：J是航天器的惯性张量。

定义如下矩阵

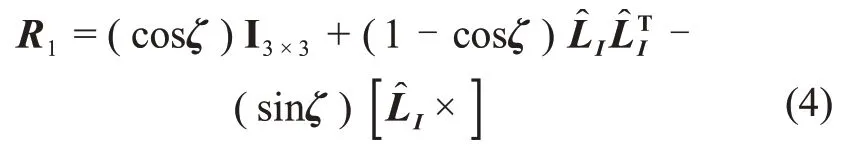
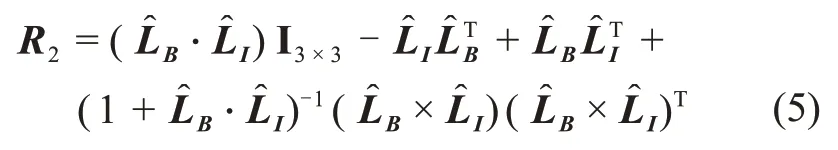
则方向余弦矩阵可按下式计算为

其中：ζ定义为旋转角。

其运动学方程满足

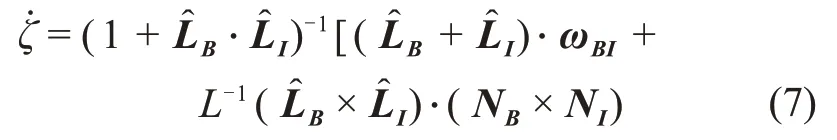
1.3 双目相机观测模型

本文利用服务航天器所携带的双目相机对目标进行连续观测，并通过图像处理技术识别和跟踪卫星表面的N个特征点，从而实现相关参数的估计。对于任意特征点Pi，i=1,…,N，其在相机左右相平面上的投影像素坐标分别为(uli,vli)和(uri,vri)。同时可以利用光流技术获得像素点在成相平面上的移动速度令特征点相对于相机坐标系的矢量为ρi=OCPi，根据双目相机的三角测量原理，可以恢复ρi及其导数在相机坐标系{C}下的展开形式，即[18]

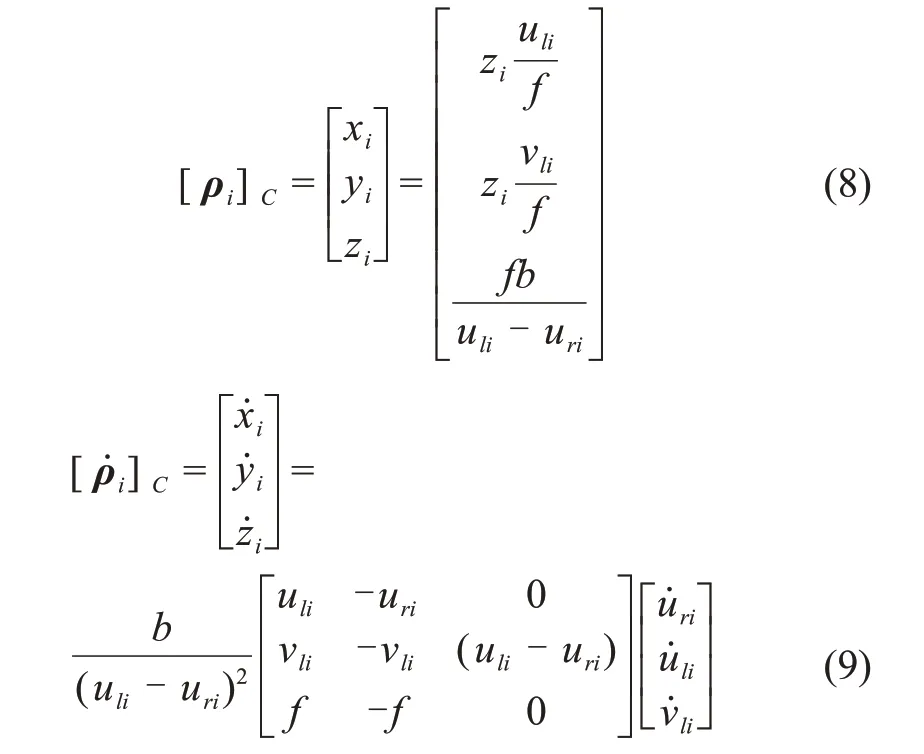
其中：f为相机焦距；b为基线距离。

由转移定理可知，ρi在惯性系下的位置与速度分别为

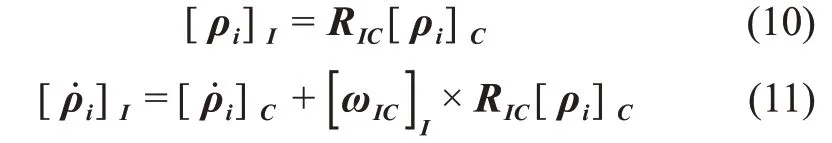
其中：RIC和ωIC分别是相机坐标系相对于惯性系的姿态和角速度，可由服务航天器的姿态确定系统结合双目相机在航天器上的安装方位通过计算获得。

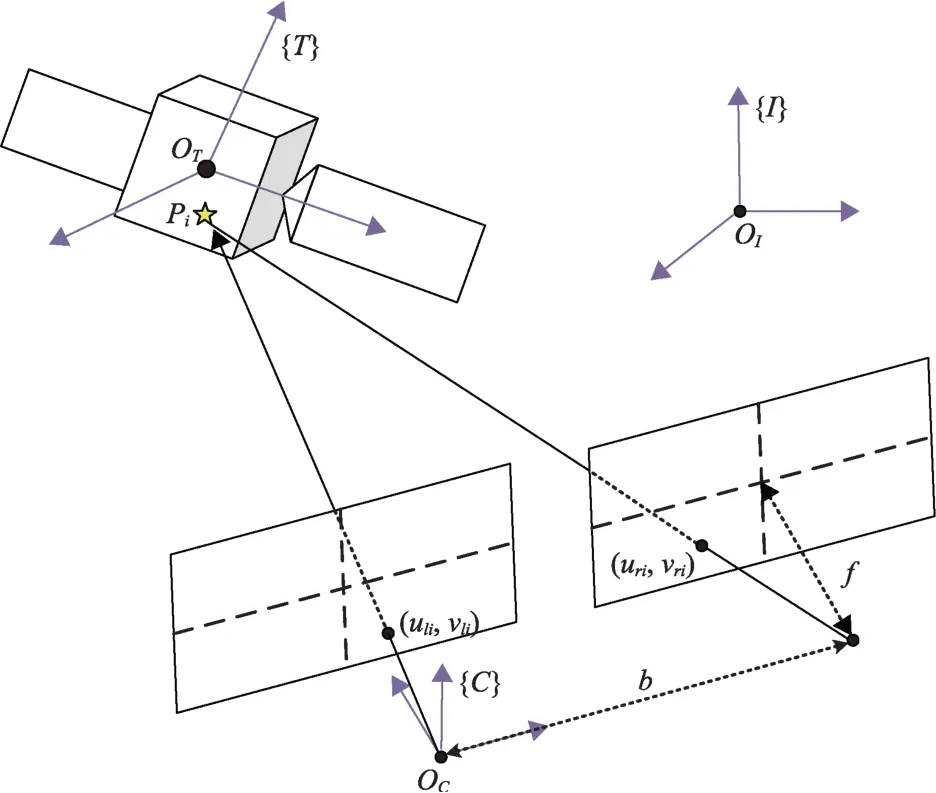
图1 双目视觉测量模型Fig.1 Measurement model of stereo vision

2 导航滤波器设计

2.1 状态方程

导航滤波器的状态为非合作目标的Markley变量

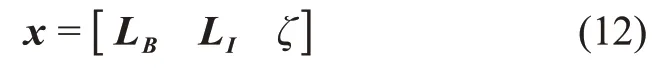
相应的动力学方程

并由式（1）、（2）、（7）组成。其中，ϖ为相应的过程噪声。

2.2 测量方程

导航滤波器的测量方程需建立观测量与状态的函数关系。令目标航天器的质心为OT，则特征点Pi的相对位置可分解如下形式为

其中：ρ0=OCOT表示目标质心与相机的相对位置；ri=OTPi表示特征点Pi相对目标质心的位置。

对式（14）在惯性系下求导，可得

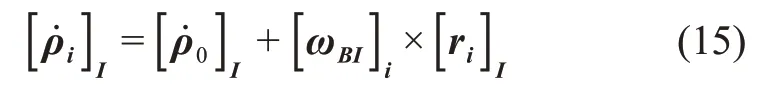
由于服务对象属于非合作目标，且一般并非为交会对接任务进行设计，其表面通常未安装用于辅助测量的标识。而所测量的特征点是由图像处理算法直接得到，具有一定的随机性，其与目标质心的相对位置关系通常未知。此时可引入另一特征点Pj，且其亦满足式。令二式相减，可得

式（16）的化简用到了恒等式ri-rj=ρi-ρj。可通过对特征点的位置与速度进行两两作差，建立特征点相对矢量的运动与目标旋转角速度的关系，从而抵消特征点本身与质心位置关系不确定性的影响，如图2所示。对于N个特征点的情况，可生成的相对矢量个数为组合数据此，滤波器的测量方程可写成如下形式

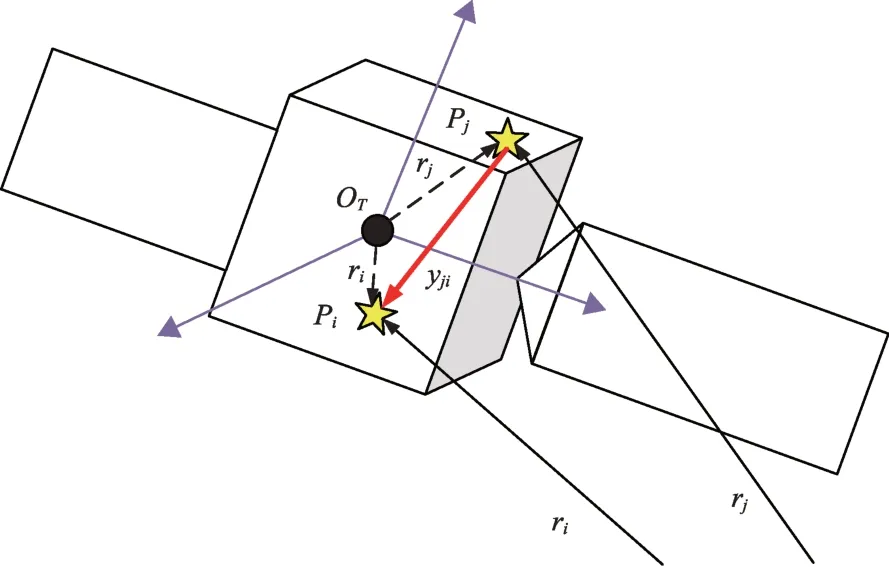
图2 特征点观测模型Fig.2 Measurement modeling of feature points

因此，滤波器总的测量矢量为

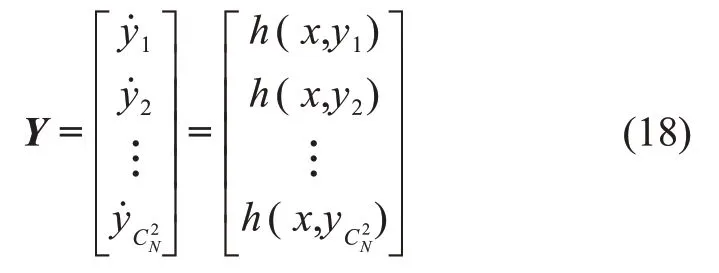
2.3 滤波算法

系统的状态方程与测量方程均为非线性方程，需采用适用于非线性系统的滤波算法。本文采用此处采用容积卡尔曼滤波方法（Cubature Kalman Filter，CKF）。CKF是一种基于三阶球面-径向规则的滤波方法，采用2n个容积点对随机变量的一、二阶矩进行近似（n为状态维数），与扩展卡尔曼滤波器（Extended Kalman Filter，EKF）相比，精度更高并且避免了求雅各比矩阵；与无损卡尔曼滤波（Unscented Kalman Filter，UKF）相比，避免了参数调节，并且理论上能够确保协方差矩阵的正定性[19-20]。和UKF不同，CKF算法舍掉了中心采样点，并按照下式进行容积点和权重的取值。

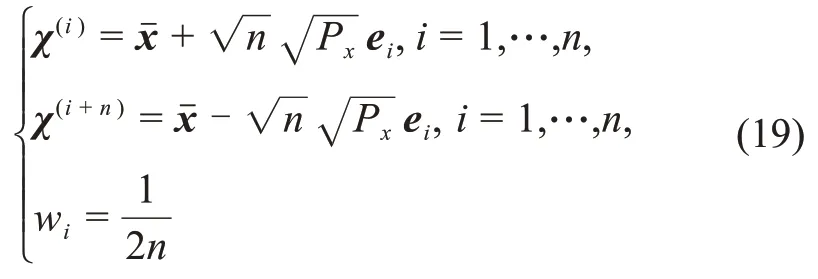
完整的CKF算法如下

1）初始化

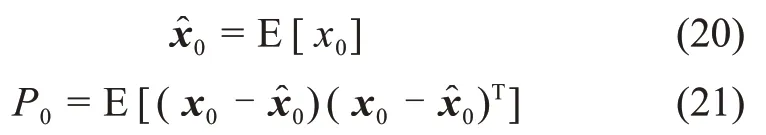
2）状态预测

Step1 容积点与权值计算

Step2 一步预测的矩近似

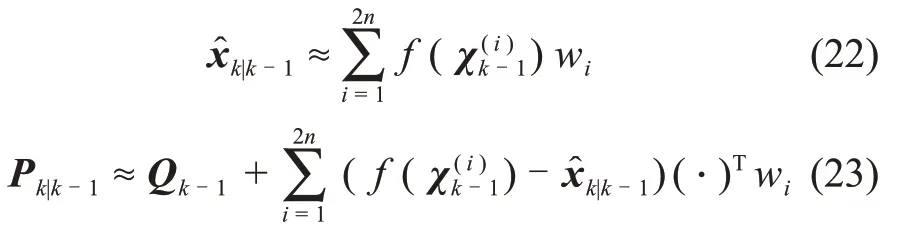
其中：Qk-1为过程噪声协方差矩阵。

3）测量更新

Step1 容积点与权值计算

Step2 测量更新的矩近似

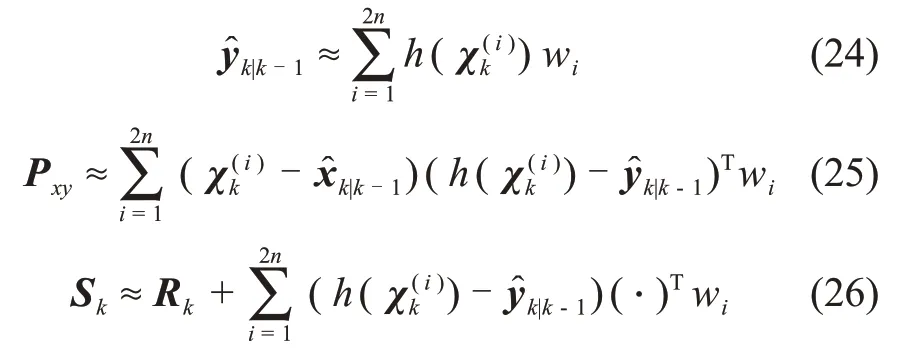
其中：Pk为测量噪声协方差矩阵。

Step3 后验均值与方差估计

3 仿真分析

本节利用计算机仿真对所提出的算法进行验证。目标的自旋轴方向估计误差自旋轴方向误差Δθ与角速度误差Δω分别定义为

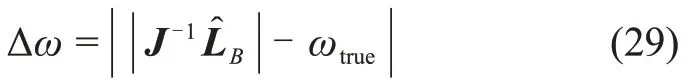
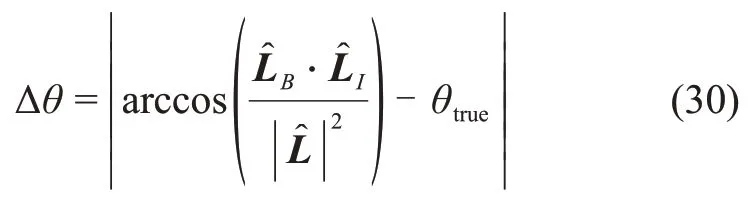
在实际的导航过程中特点需通过SIFT（Scale-Invariant Feature Transform）、SURF（Speeded-Up Robust Features）等图像处理算法进行提取和跟踪。本文旨在验证所提出的导航滤波算法，因此假定图像特征提取步骤已经完成。在仿真过程中将根据航天器表面特征点的运动规律直接生成相应的特征点轨迹数据。同时本文假定目标不受外力矩影响，可将NB和NI视为零均值的噪声。

仿真参数设定为：目标航天器的转动惯量分布为J=diag（[1 300，1 300，2 200]）kg·m2。过程噪声协方差矩阵为Q=10-8×I7×7。令自旋轴方向矢量为l=[0 0.707 1 0.707 1]T，此时LB和LI之间的夹角为θtrue=45°。数值积分采用Matlab内置的ode45函数，滤波周期0.1 s，仿真时间300 s。

为研究航天器运动，特征识别结果以及测量条件等因素对姿态估计精度的影响，分别设置了3组仿真，对应参数的设定和仿真结果如下。

1）不同的航天器自旋角速度

在目标本体系下3个主轴方向[-2,2]m 的范围内选取N=6个特征点，并令特征点相对位置与速度的测量噪声为R=10-4×I6×6。分别设置航天器的自旋角速度为ω为2、5、8、10°/s，对应的结果如图3～4所示。仿真结果表明：随着航天器自旋速度的增加，对于角速度估计的估计效果越好。这是因为当航天器自旋速度较慢时，特征点间的相对速度较小，在同样的测量条件下受测量噪声影响而产生的相对误差较大。从ω在2～5°/s这一角速度变化范围内，估计精度与收敛速度均存在明显的提升。而随着角速度的进一步增加，其对于估计精度的提升不明显。同时，角速度对于自旋轴方向的估计的影响不明显。

2）不同的特征点个数

令航天器的自旋角速度为ω=10°/s，测量噪声为R=10-4×I6×6。选取特征点个数分别为N为整数，取值范围为[1,6]，对应的结果如图5～6所示。仿真结果表明，一方面仅依靠观测两个特征点也能实现自旋角速度和自旋轴方向较高精度的估计；另一方面随着估计效果会随着特征点数量的增加而提升。当特征点数量从N=2增加到N=3时，角速度的收敛速度存在较大程度的提升。随着特征点个数的进一步增加，估计精度和收敛速度的提升不明显。此外，特征点个数的变化对于自旋轴方向的估计精度影响不大。

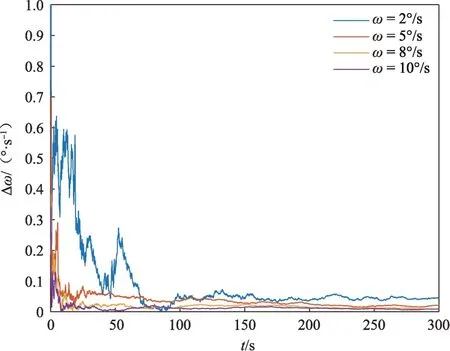
图3 自旋角速度误差（不同角速度）Fig.3 Estimation error of spinning angular velocity（different angular velocity）

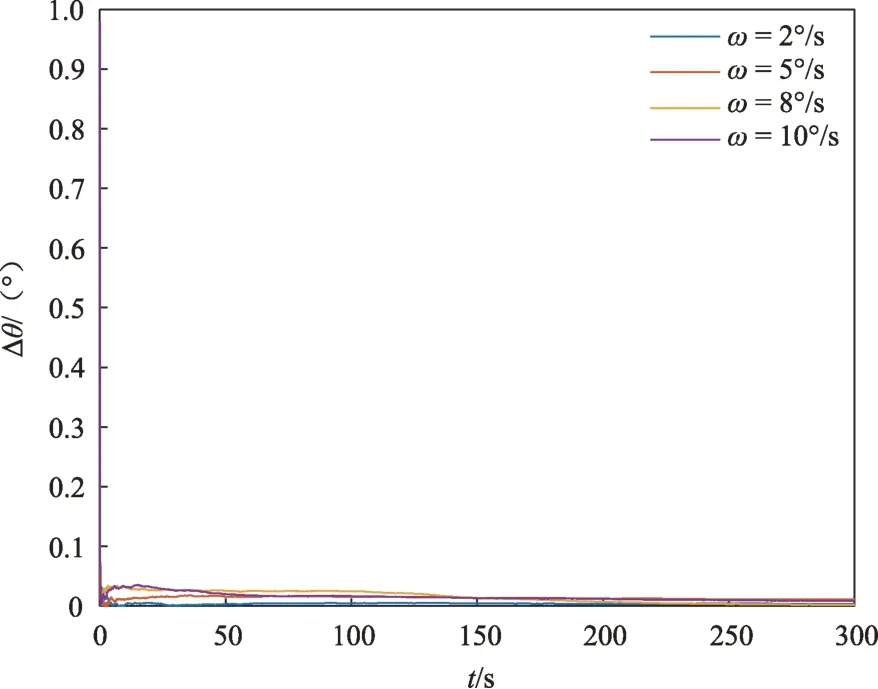
图4 自旋轴方向误差（不同角速度）Fig.4 Estimation error of direction of spinning axis（different angular velocity）

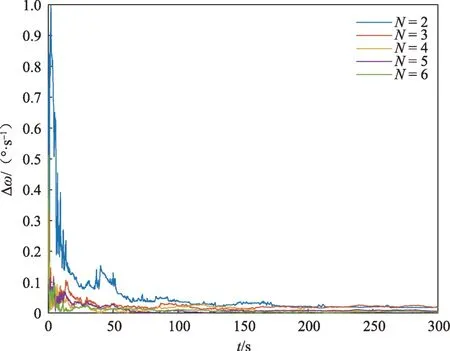
图5 自旋角速度误差（不同特征点数量）Fig.5 Estimation error of spinning angular velocity（different number of feature points）

3）不同的测量噪声统计特性

令航天器的自旋角速度为ω=10°/s，并选取特征点的个数为N=6。设测量噪声协方差阵为R=r×I6×6，并令参数r分别取10-3、5×10-4、10-4、5×10-5，对应的结果如图7～8所示。仿真结果表明，随着测量精度的提高，自旋角速度和自旋轴的估计精度均有提高。由于角速度的估计完全依赖于对目标表面特征点的观测。测量噪声的统计特性对于估计精度有直接影响。而当测量精度提高到一定程度之后，滤波算法的估计精度则开始受到过程噪声的制约。

通过上述仿真对比实验可以发现：目标更快的自旋速度、更多的目标表面特征点数量以及更高的测量精度均有助于提高自旋角速度的估计精度。而自旋轴指向的估计精度主要受测量精度的制约。Liu等[21]指出，近距离相对导航的姿态测量需满足姿态角精度1°，角速率精度0.2～0.1°/s。仿真结果表明，本文所提出的基于双目视觉的角速度与自旋轴估计方法能够满足上述精度要求。

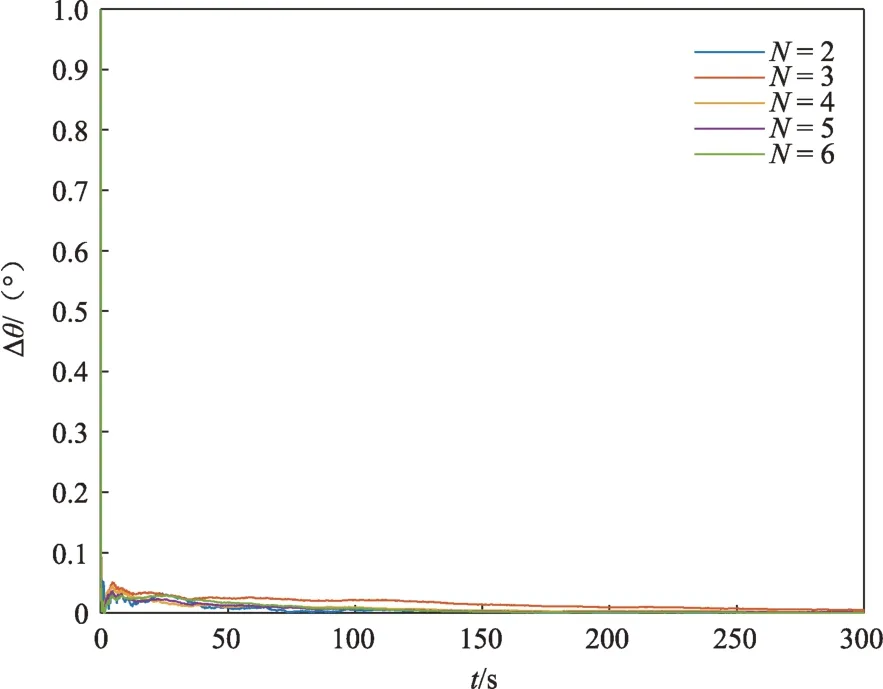
图6 自旋轴方向误差（不同特征点数量）Fig.6 Estimation error of direction of spinning axis（different number of feature points）

需要特别说明的是，由于最少N=2 个特征点即可实现姿态的有效估计，而检测与跟踪更多的特征点一方面对图像处理算法的要求较高，另一方面也会增加计算的负担。因此，在估计精度要求不高或相机测量跟踪精度较高的情况下，采用较少数量的特征点亦可满足导航要求。而对于光照条件恶劣或目标自旋速度较慢的情况，往往需要观测更多的特征点来保证算法的精度。在实际的在轨服务相对导航方案设计过程中，需结合服务对象的运动特性，算法精度的要求，光学测量的环境以及星载计算机的运算能力等方面因素来对特征点的使用进行取舍。

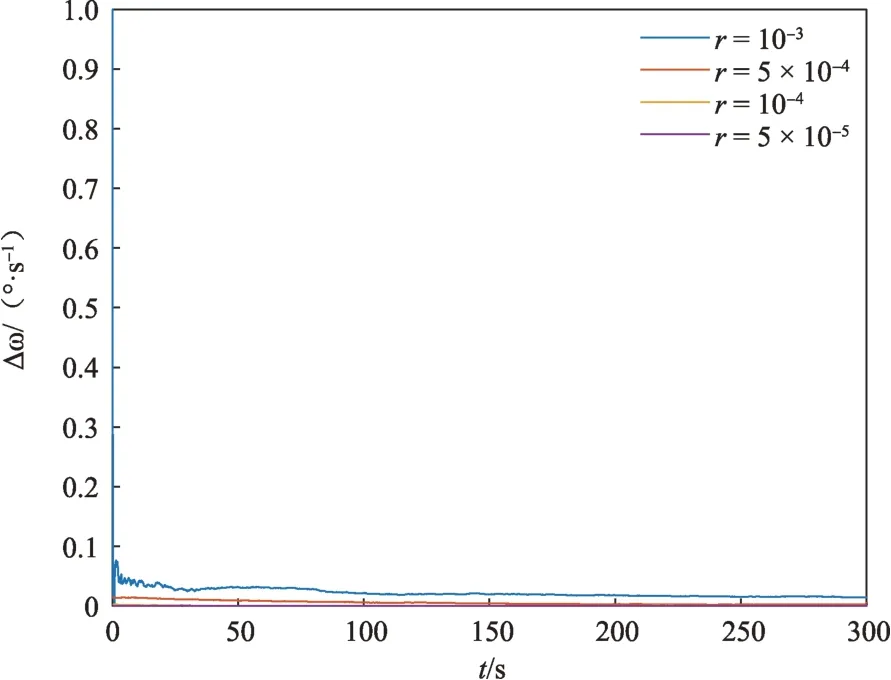
图7 自旋角速度误差（不同测量噪声级别）Fig.7 Estimation error of spinning angular velocity（different measurement noise level）

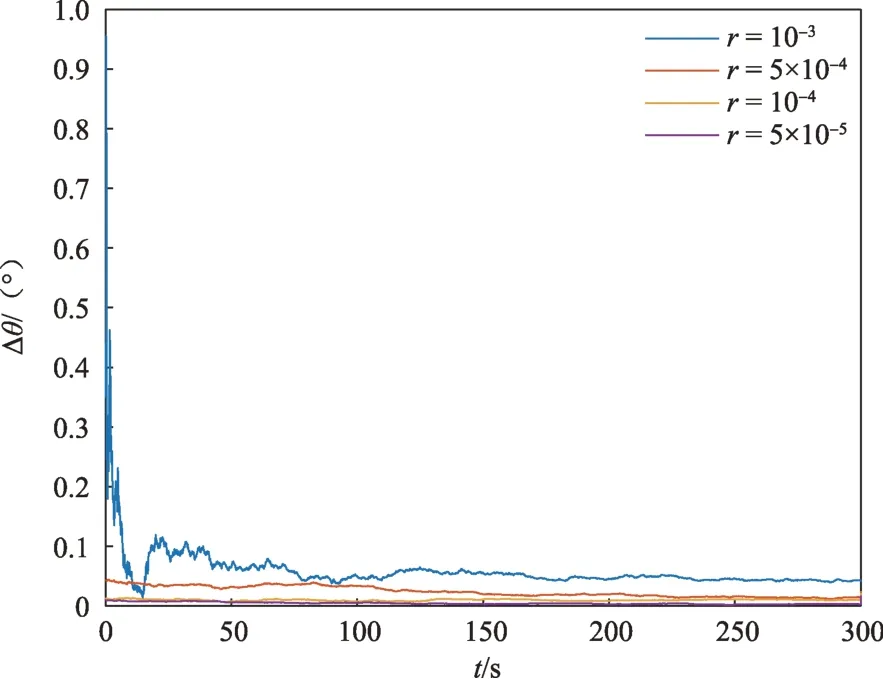
图8 自旋轴方向误差（不同测量噪声级别）Fig.8 Estimation error of direction of spinning axis（different measurement noise level）

4 结 论

针对空间在轨服务对于相对导航技术的需求，本文提出了一种基于Markley变量与双目视觉测量的空间非合作目标姿态估计方法。文章首先推导了基于Markley变量的卫星动力学方程和双目相机观测方程；其次研究了目标表面特征点的运动规律并设计了相应的导航滤波器；最后利用数值仿真分析了对姿态估计精度的影响。针对可能影响估计精度的因素分别进行了数值仿真与分析。仿真结果表明，本算法能够有效地估计目标的自旋角速度与自旋轴指向，其精度能够满足近距离相对导航的要求，因而对于面向在轨服务的相对导航技术研究具有一定参考价值。后续研究工作将通过搭建半物理仿真实验平台，利用双目相机获取目标的真实图像，结合图像特征提取匹配跟踪技术对所提出的算法进一步验证。