基于神经网络的卫星控制系统故障识别方法

孙博文，何章鸣,2，王炯琦

（1.国防科技大学文理学院，长沙 410073；2.中国空间技术研究院北京宇航系统工程研究所，北京 100094）

引 言

提高系统运行的安全性与可靠性，及时检测故障，并完成故障识别，成为当今时代研究的热点问题[1-4]。为了使设备实现预定的任务目标，同时满足系统运行的稳定性、鲁棒性等要求，通常对系统施加闭环控制。通过闭环控制调节，减少外界扰动对系统运行的影响，使得系统更具鲁棒性。因此，闭环控制系统已经被广泛应用于工业生产与控制领域，小到机械机床控制，大到航天器控制[5-6]。但是，引入闭环控制，使得系统故障诊断性能下降，原因主要有以下2 个方面[7]：①闭环控制通常会使得系统对于外部扰动更鲁棒，但当故障处于早期阶段或故障值较小时，所带来的影响可能是故障信号被控制量所掩盖，使得故障难以被检测，从而导致更高的漏报率；②控制系统的反馈调节可能使得故障在系统内部传播，导致同一故障模式下多处变量/信号发生异常（降低了故障幅值）或正常/故障以及不同故障模式下系统状态/变量异常特征相似（降低了故障特征差异），使得故障特征具有较强的耦合性，从而增加了故障识别难度。

针对闭环控制系统的故障识别，国内外专家学者也做了一些研究[8-13]，可以分为3 个方面：基于模型的方法、基于知识的方法和基于数据驱动的方法。

1）基于模型的方法

Macgregor 等[8]回顾分析了线性输入输出模型的闭环系统识别结果，利用渐进预测误差平方和的频域表达式对其进行解释，并且分析了噪声模型和数据滤波器对过程动态模型的可识别作用。Ghantasala 等[9]提出了一种基于控制约束和执行机构故障的非线性抛物型偏微分方程建模的故障检测与识别的设计与实现方法。在闭环控制系统的故障识别中，基于模型的方法具有一定的局限性，对于一个复杂的、无法用一个准确模型表示的系统，基于模型的故障识别方法往往达不到理想的效果。

2）基于知识的方法

Hamad等[10]研究了在闭环控制系统中基于汽车发动机的故障检测与识别方法，通过使用独立径向基函数神经网络模型来模拟发动机动力学，利用模型误差建立残差。针对预测电动液压缸驱动中的泄露流量大小以及泄露类型问题，Le 等[11]利用多层感知机神经网络进行动态特征提取，通过使用压力瞬态响应作为信息，同时考虑了单泄露和多泄露故障，还分别考虑了串行和并行2种网络模型的性能。

3）基于数据驱动的方法

在数据驱动方法中，可以通过子空间算法给出闭环数据的偏差估计。Wang 等[12]给出了一种新的子空间识别法，即通过主成分分析的子空间识别法，给出了闭环控制系统的确定性部分和随机部分的一致估计，然后引入列加权作为改进方法的效率/准确度。Wang 等[13]开发了一种用于多输入多输出线性动态闭环控制系统传感器诊断方案，以识别不同类型的传感器故障（偏置、漂移和精度降级），特别是对于初期的传感器故障。

闭环控制系统故障识别方法分类如图1所示。神经网络[14-17]具有自主学习的特点，可以通过反复训练得到各个模式数据的特征，有望得到较好故障识别率。正因如此，可应用基于神经网络的故障识别方法提高故障识别的性能。

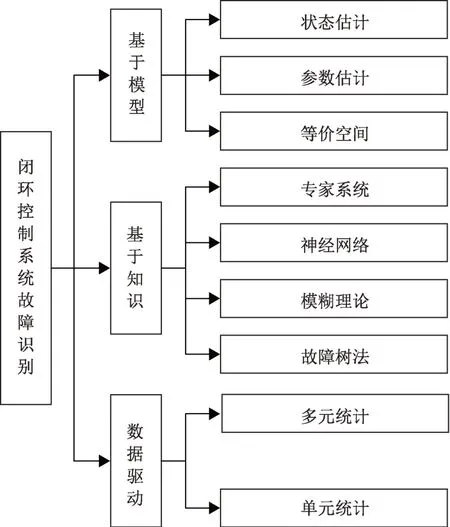
图1 闭环故障识别方法分类Fig.1 Classification of close-loop fault identification methods

本文提出一种基于神经网络的系统故障识别方法，对有标签的数据有着很好的识别效果。利用带标签的训练数据对每一类模式进行有监督学习，将测试数据输入到已经训练好的神经网络中进行分类，从而可以实现了闭环控制系统的故障识别。

1 SISO模型分析

考虑如下开环模型

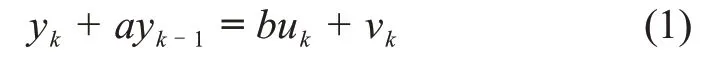
其中：yk和uk分别是模型的输入和输出变量；vk是白噪声。

采用如下辨识准则

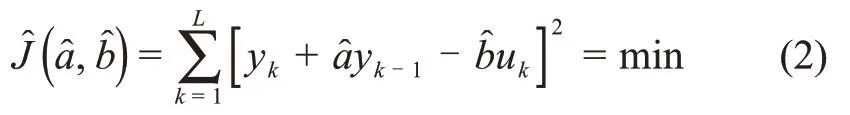
显然，参数[a,b]可以通过准则（2）计算出来。

考虑如下闭环模型

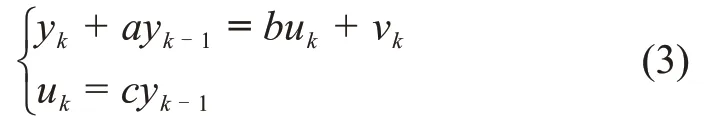
由于存在反馈作用，故

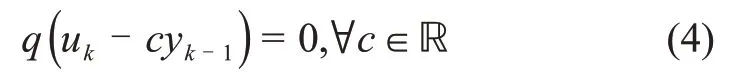
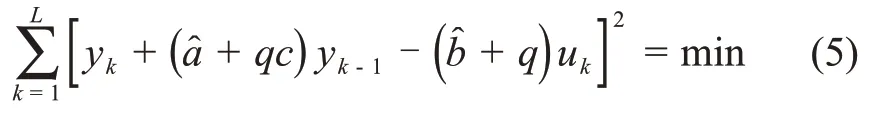
上述情况说明：对闭环系统式（3）的设计中，参数[a,b]是无法通过准则式（2）计算出来。

反馈控制破坏了开环控制系统下输入与输出之间的非线性相关性，导致开环系统原本可辨识的参数不再具有可辨识性。这会给故障诊断带来困难，下面将分类讨论。

1.1 误报率

假定真实参数[a,b]是已知的，系统没有发生故障。闭环导致准则式(2)计算出来的解一般与真实的参数[a,b]不同，使得参数残差rab不总是为零均值的。

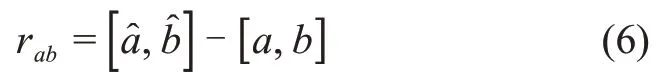
因此，在闭环系统中，基于参数辨识的方法容易出现误报。

1.2 漏报率

假定真实参数[a,b]是已知的，系统发生乘性故障，即参数由变成了由于系统存在反馈使得以下残差rk总是为零均值的。

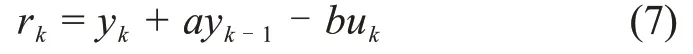
实际上，因quk=qcyk-1，故

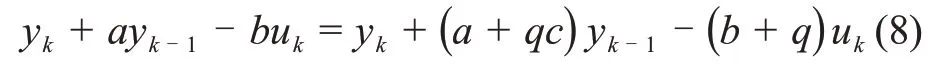
式（8）中左边为正常系统残差，右边为故障系统残差，两者相等，都为白噪声序列。

综上所述，闭环对故障诊断的影响分为2方面：①闭环可能改变了开环的可辨识性，导致误报率上升；②闭环于参数故障耦合，导致漏报率上升。

2 MIMO模型分析

考虑如下开环模型

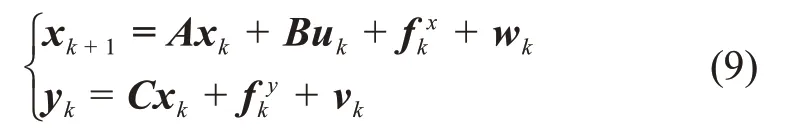
对应式（8）的闭环模型为

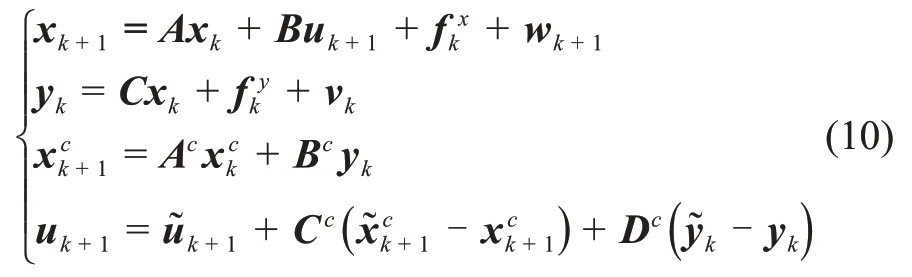
从模型式（10）中可以看出：闭环控制系统将测量值偏差-yk信息反馈给下一时刻的控制输入uk+1中，进而调节系统的运行状态。

2.1 闭环系统分析

假设系统上标中的为系统正常运转时相应变量的值。考虑k时刻发生传感器故障，即当时，系统输出变量为

根据式（2）和式（3）可知，系统输出变量影响系统控制变量，可得

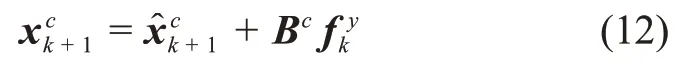
根据式（2）～（4）可知，系统输出变量和控制变量同时影响k+1时刻的系统输入变量，可得

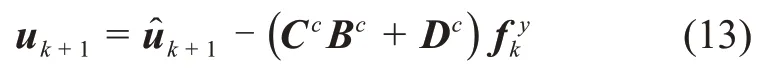
可以得到k+1时刻的系统状态变量

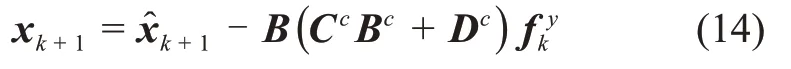
由式（14）可知，k时刻的传感器故障将会影响到k+1时刻的系统输出，其关系为

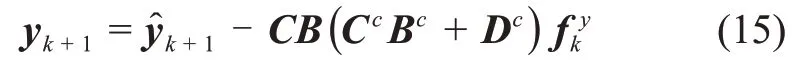
令

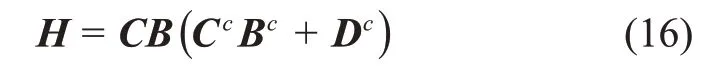
其中：QH为特征向量组成的矩阵；ΛH=其中λ2>…>λl>0，l=rank(H)。

2.2 闭环对传感器故障的影响

由传感器故障的传播过程可知，若系统在k时刻传感器发生故障，即故障值此故障对k+1时刻的系统输出的影响为若闭环控制系统选取适当，即当H的特征值λ1,λ2,…,λl均小于1时，在k+1时刻故障值将消减。

依此类推，当迭代至k+p时刻时，k时刻发生的传感器故障值将降为考虑

由于引入闭环控制率，闭环控制系统可以逐渐降低传感器故障对系统的影响。

若k+1时刻传感器仍发生故障，其故障值为此时在k时刻和k+1时刻同时影响下，k+1时刻在系统输出变量表现的故障值为在负反馈调节中，可以选取适当的系数矩阵使得故障对系统的影响降低，即从而降低了传感器故障对系统的影响。

3 基于神经网络的故障识别方法

3.1 神经网络原理

神经网络已经广泛地应用于各个领域，但是传统的单层神经网络本身存在着一定的局限：无法满足复杂系统的分类需要。文献[14]提到的神经网络可以解决了这一问题。神经网络是一种包含2层以上隐含层的多层神经网络，与传统的单层神经网络相比有着增强拟合的效果，可以对复杂数据进行分类识别的优势。正因如此，可以更好地训练出各个模式类数据的特征，增大不同模式的识别率。

设a=[a1,a2,…,an]T为输入层数据，b=[b1,b2,…,bl]T为神经网络的输出值，Wi,i=1,2,…,q为输入信号的权重，θi,i=1,2,…,q为偏置，φi,i=1,2,…,q为激活函数。在给定前一层激活的条件下，每个隐藏层计算条件独立单元的激活。若第j个隐含层的输入为vl-1（即为第j-1个隐含层的输出），那么第l个隐含层的输入可以由下式计算求得

其中：Wj和θj分别为第j层的权值矩阵和偏置向量；φj(·)为预先定义的非线性激活函数。

在训练过程中，为使训练可以采用梯度下降法对权值矩阵W和偏置θ进行更新，为

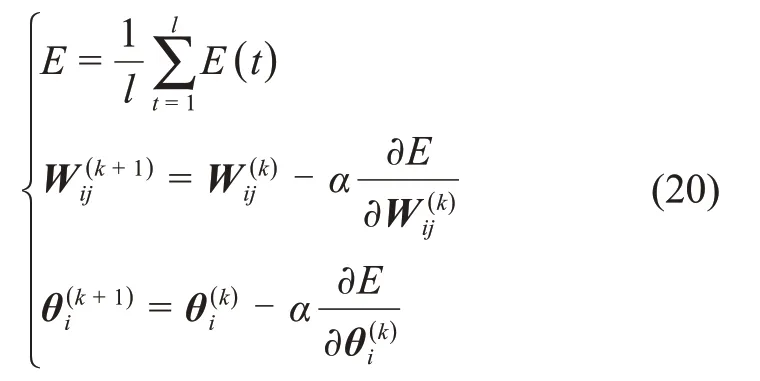
其中：α为学习效率；k表示学习次数；E为单个样本的输出数据训练误差E(t)的均值。

假设有m个训练样本，而训练误差由理论标签β与实际输出d的距离决定，习惯用其二范数定义，为

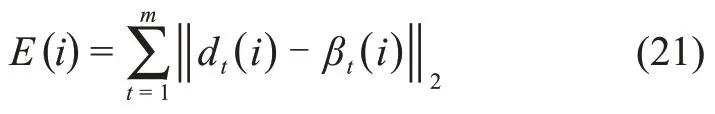
当误差满足条件或者达到预设训练次数时停止训练。

3.2 基于神经网络的故障识别方法

基于神经网络的故障识别方法如下：

Step 1.首先将已分类的训练数据进行预处理，设定合适的滑动窗口长度，然后按照设定好的滑动窗口将数据进行重新排列，完成数据的预处理；

Step 2.选择好合适的网络结构，预先设定网络的隐含层数，输入层、输出层以及各隐含层的节点数，建立学习神经网络结构；

Step 3.将训练数据带入该神经网络，选择合适的激活函数进行有监督的训练过程；

Step 4.将待测数据代入已训练好的神经网络中，记录输出结果从而进行待测数据的分类；

Step 5.计算神经网络总识别率以及各个模式数据的识别率，得到各识别率随窗口长度变化的关系。

4 仿真分析

4.1 算例1：SISO系统

开环SISO模型如下

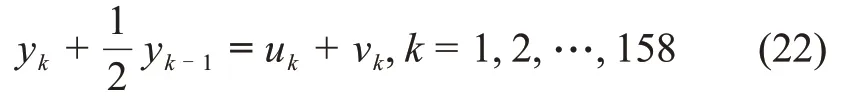
其中：输入数据为uk=sink；白噪声vk的标准差为0.001，也就是说真实参数为[a,b]=[-1/2,1]。

开环输入和输出数据如图2所示。设计矩阵的条件数很小为1.194 6，最小二乘法辨识的参数为辨识误差很小。

假定闭环控制律为

输出的初始值为y1=1，则闭环输入和输出数据如图3所示。设计矩阵的条件数很大，为2.176×1016，最小二乘法辨识的参数为[a,b]=[-1,0]，辨识误差非常大。这势必引起误报率提高。另外，从第100个样本开始，当确实发生参数故障，[a,b]=[-1/2,1]突变为[a,b]=[1/2,3]，但是检测残差在k=100前后却是白噪声，如图4所示，这势必引起漏报率上升。

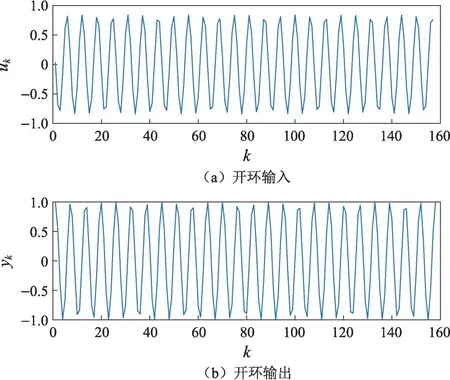
图2 SISO系统开环输入输出数据Fig.2 I/O data of the open-loop SISO system

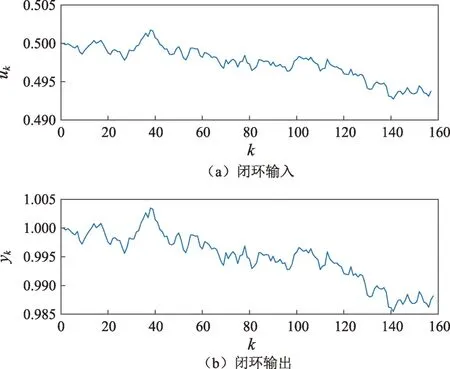
图3 SISO系统闭环输入输出数据Fig.3 I/O data of the close-loop SISO system

4.2 算例2：卫星姿态控制系统

表1为卫星姿态控制系统中的7个变量，分别为地球敏感器的横滚角与俯仰角、太阳敏感器的横滚角与俯仰角以及陀螺仪的横滚角、俯仰角与偏航角。本实验共收集3个模式下的数据，分别为正常数据，地球敏感器俯仰角故障数据和太阳敏感器俯仰角故障数据，其中正常数据样本容量为501，2类故障数据样本容量均为143。正常数据与故障数据如图5～7所示。

图4 SISO闭环检测残差Fig.4 Detection residual of the close-loop system

表1 SACS变量Table 1 The variables from SACS

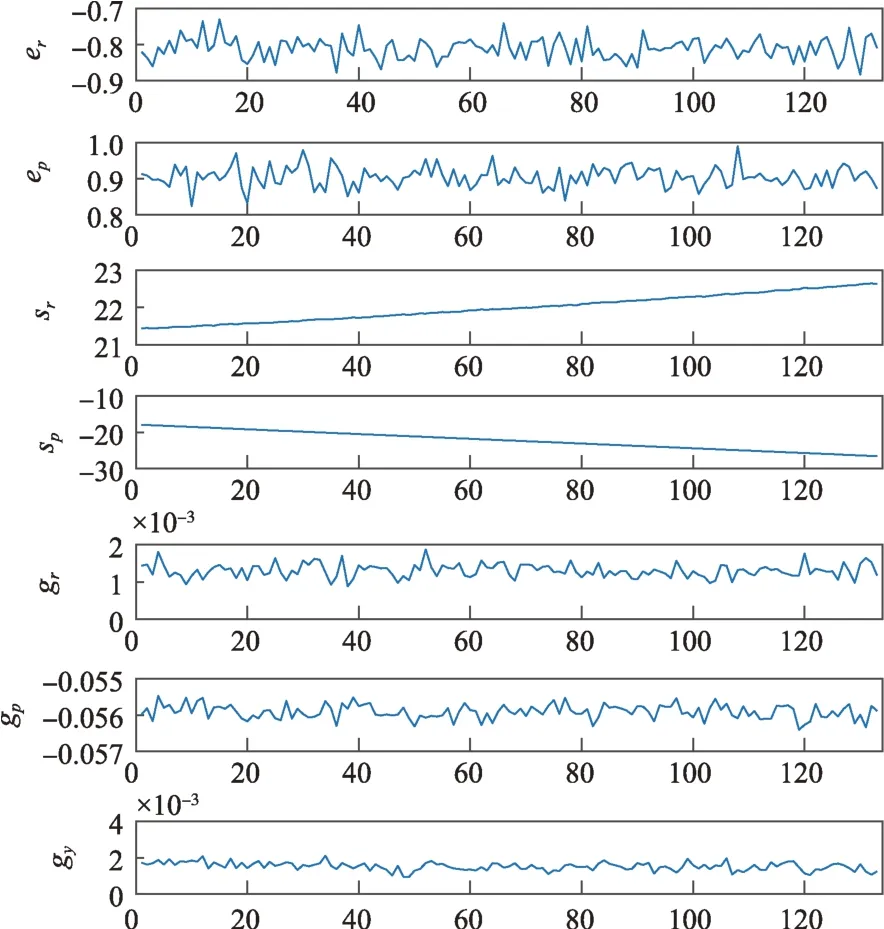
图5 正常数据Fig.5 The normal data

每类数据中选取50%训练神经网络，训练次数为2 000次，该网络共有3个隐含层，第1个隐含层设置10个节点，激活函数采用Sigmoid函数；第2个隐含层设置为5个节点，激活函数同样采用Sigmoid函数；第3个隐含层设置为3个节点，激活函数采用Softmax函数。窗口长度与各指标的关系如表2所示，随着窗口长度的增加，各种模式的识别率也随之增加，总识别率分别为96.601%、99.680%、99.739%，这说明引入滑动窗口来改进神经网络确实有效。

仿真对比了基于距离识别方法、角度识别方法和神经网络方法，他们的总识别率分别为99.739%、83.31%、76.79%。显然，相对于传统的基于距离或基于角度的识别方法，本文提出的方法有效提高了故障识别率。

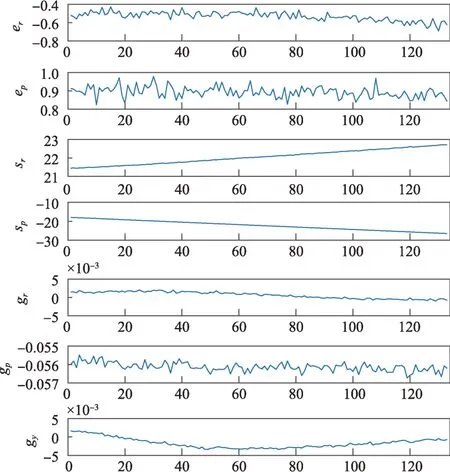
图6 第1类故障数据Fig.6 The 1st fault data

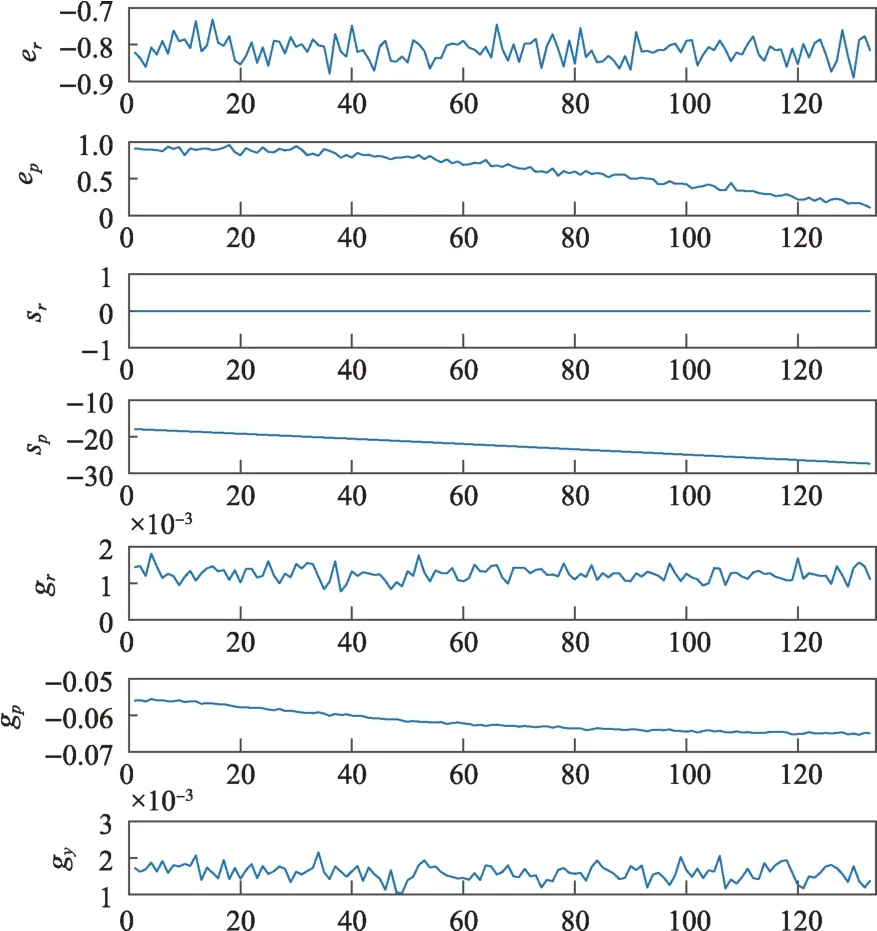
图7 第2类故障数据Fig.7 The 2nd fault data

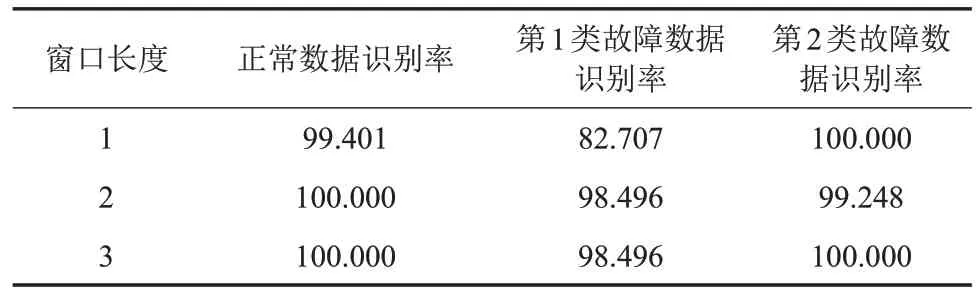
表2 窗口长度与各指标关系Table 2 The relationship between the moving window size and the identification performance %

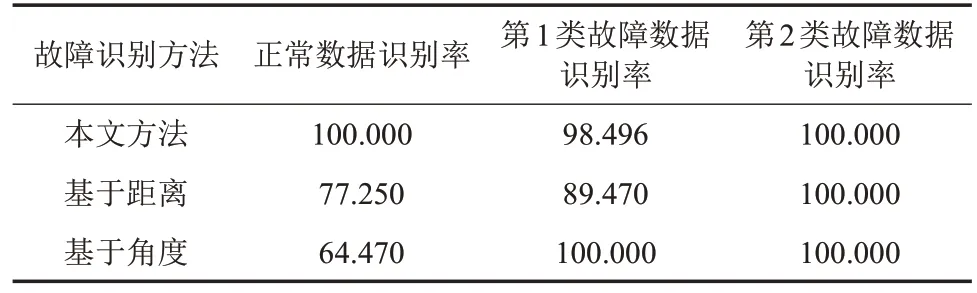
表3 不同方法的识别率Table 3 The comparative identification performance of all methods %

5 结 论

本文分析了闭环结构对SISO和MIMO系统可辨识性、误报率、漏报率、故障幅值的影响。从理论上分析了闭环控制系统的特点，不同故障的传播机理及其对系统输出变量的影响关系，揭示了闭环控制系统故障识别的困难所在，最后构造了基于神经网络的闭环故障算法，并通过纯数值仿真及卫星姿态控制系统仿真验证了理论分析结论和故障识别算法的有效性。