自识别自校准Kalman滤波方法

傅惠民，杨海峰，文歆磊

（北京航空航天大学小样本技术研究中心，北京 100191）

引 言

Kalman滤波（Kalman Filter，KF）自20世纪60年代被提出以来，在各工程领域得到了广泛应用[1]。在其基础上，扩展Kalman滤波（Extended Kalman Filter，EKF）[2-3]、无迹Kalman滤波（Unscented Kalman Filter，UKF）[4-7]、粒子滤波（Particle Filter，PF）[8]和秩滤波（Rank Filter，RF）[9-10]等方法也得到了长足发展。但是在工程实际中，受到环境因素的影响、模型和参数的选取不当等原因，状态方程往往受到未知输入的影响[11-13]，结果导致较大滤波误差。针对有未知输入的情况，傅惠民等分别针对线性系统和非线性系统提出了自校准Kalman滤波方法（Self-Calibration Kalman Filter，SCKF）[14]和自校准扩展Kalman滤波方法（Self-Calibration Extended Kalman Filter，SCEKF）[15]，能够对未知输入进行估计和修正，从而有效提高滤波精度。

在此基础上，本文进一步提出了一种自识别自校准Kalman滤波方法，它首先能够对状态方程中有无未知输入自动进行识别，当存在未知输入时再对该未知输入进行估计和补偿，从而提高滤波精度。在工程实际中无论有无未知输入，采用本文方法都优于传统Kalman滤波。

1 线性系统自识别自校准滤波方法

1.1 线性系统方程

工程上，状态方程中含有未知输入的线性离散系统一般可表示为

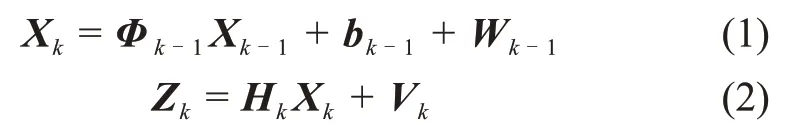
其中：Xk表示m维系统状态向量；Zk表示n维系统量测向量；bk表示状态方程中的未知输入；Φk和Hk分别为系统状态矩阵和量测矩阵；Wk和Vk分别为状态噪声向量和量测噪声向量，其方差矩阵分别为Qk和Rk，并且满足

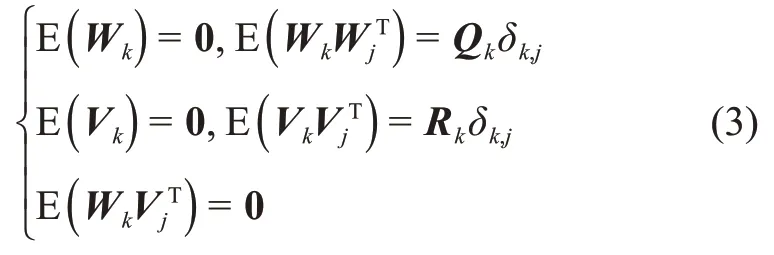
其中：E(·)为数学期望符号；δk,j为δ函数，当k=j时，δk,j=1，当k≠j时，δk,j=0。

1.2 线性系统未知输入自识别自校准

由于状态方程中含有未知输入，因此需要根据自校准原理对状态方程中的未知输入bk-1进行估计。

工程上，当相邻两次滤波的时间间隔足够小时，未知输入bk-1往往不会发生较大的变化。因此当k≥3时，状态方程中的未知输入bk-1可近似表示为

由式（1）和式（4）可得状态未知输入bk-1的初始估计值为

1.3 线性系统滤波步骤

首先进行滤波初始化

当k=1,2时，一步预测为

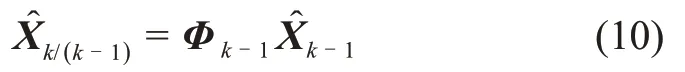
一步预测误差协方差矩阵为

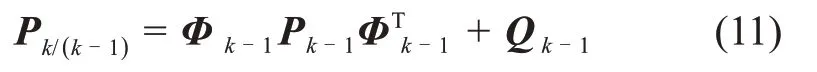
状态估计为

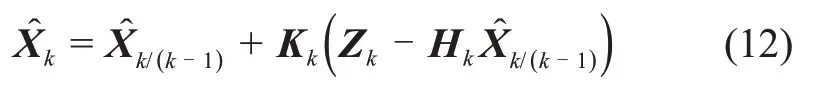
状态估计误差协方差矩阵为

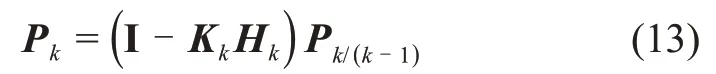
滤波增益矩阵Kk由下式给出

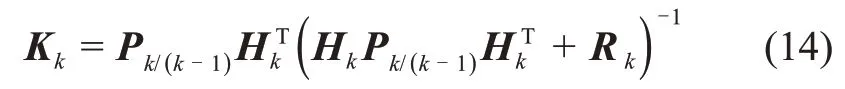
当k≥3时，首先通过自识别自校准得到未知输入估计bk-1，然后按下面步骤进行Kalman滤波，一步预测为

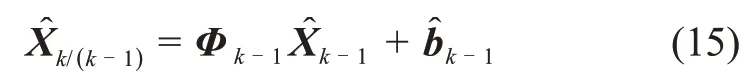
一步预测误差协方差矩阵为

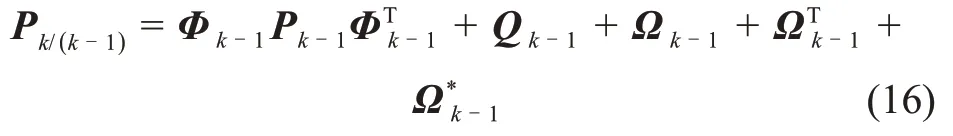
式中

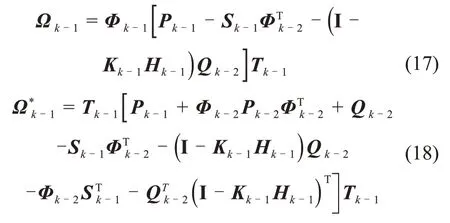
其中：I为单位矩阵；Tk-1为当bk-1,j≠0时第j行、第j列元素为1，当bk-1,j=0时第j行、第j列元素为0，其余非对角线上元素均为0的对角矩阵；Sk-1为

其中：状态估计、状态估计误差协方差矩阵Pk和滤波增益矩阵Kk分别由式（12）～（14）给出。

2 非线性系统自识别自校准滤波方法

2.1 非线性系统方程

工程上，状态方程中含有未知输入的非线性离散系统一般可表示为

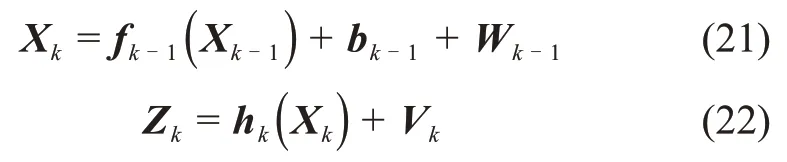
其中：fk(·)和hk(·)均为非线性向量函数；Xk，Zk，bk，Wk和Vk的意义与式（1）和式（2）相同。

2.2 非线性系统未知输入自识别自校准

同样，当k≥3时，由式（4）和式（21），可得状态未知输入bk-1的初始估计值为

旅游院校思政教育工作很重要，这项工作的有效开展能够全面提升旅游人才的思想政治水平，觉悟水平，道德素养水平，是优秀旅游人才培养的关键。在新时期，旅游院校思政教育工作要不断实现教育内容和方式的创新，增强教育的新引力和感染力，这样，教育的效果才能保障。而在旅游院校思政教育中，应用新主旋律电影方式开展教育活动，有助于教育效果的提升，相关教育者要重视新主旋律电影的创新应用。

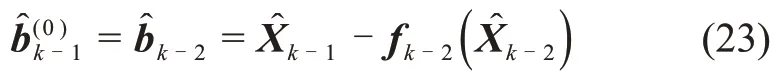
考虑到偶然误差的影响，bk-1的估计值仍由式（6）给出。

2.3 非线性系统滤波步骤

首先按照式（8）～（9）进行滤波初始化。由于状态估计误差的协方差信息无法直接通过非线性方程进行递归运算，需对式（21）～（22）的非线性系统方程进行线性化。

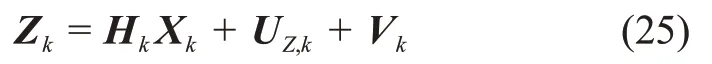
式中

当k=1,2时，一步预测为

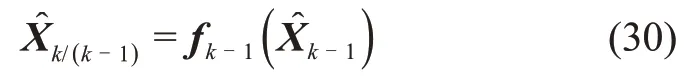
一步预测误差协方差矩阵Pk/(k-1)由式（11）计算。状态估计为

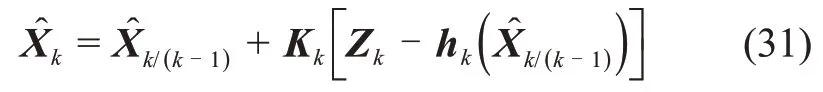
状态估计误差协方差矩阵Pk和滤波增益矩阵Kk分别由式（13）和式（14）给出。

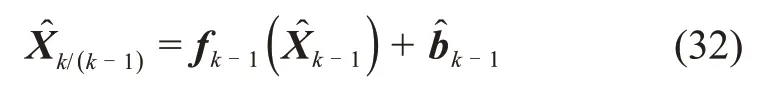
一步预测误差协方差矩阵Pk/(k-1)由式（16）给出，状态估计和状态估计误差协方差矩阵Pk则分别由式（31）和式（13）计算。

3 仿真算例

3.1 线性系统算例

考虑如下的线性系统

其中：Xk表示系统状态值（状态初值X0=1）；Zk为量测值；wk和vk分别是服从高斯分布的零均值状态偶然误差和量测偶然误差，且分别对应方差Qk=1、Rk=10、bk-1为状态方程中的未知输入，其取值为

分别采用线性Kalman滤波方法和本文方法（c=2）进行滤波，取滤波初始值=2，误差方差初始值P0=10。对系统进行500次蒙特卡洛仿真模拟，分别求得本文方法与线性Kalman滤波的均方根误差（Root Mean Square Error，RMSE）如图1所示，均方根误差的均值如表1所示。

从表1和图1可以看到，当系统状态方程受到未知输入影响时，本文方法可以发挥自识别自校准的优势，自动对其进行估计和补偿，其滤波精度比线性Kalman滤波提高了4倍多。而当没有未知输入时，又与线性Kalman滤波结果相同。

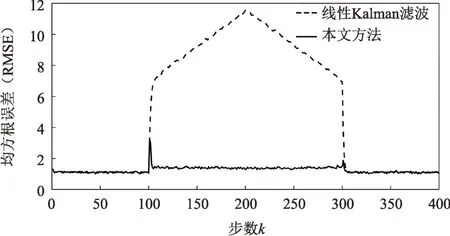
图1 本文方法与线性Kalman滤波均方根误差比较Fig.1 RMSEs comparison of proposed method and linear KF

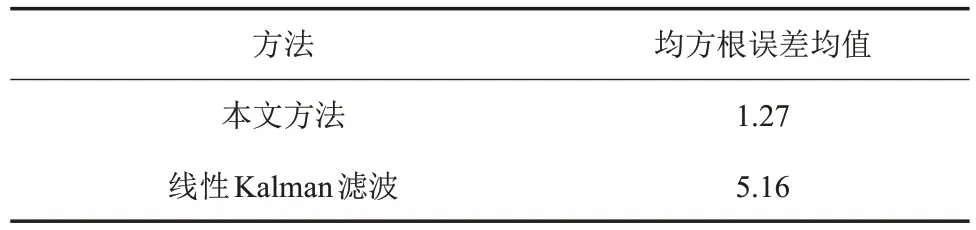
表1 本文方法与线性Kalman滤波均方根误差均值比较Table 1 RMSEs mean comparison of proposed method and linear KF

3.2 非线性系统算例

考虑如下的非线性系统

状态初值X0=100，wk和vk分别对应方差Qk=1和Rk=10，未知输入bk-1的取值为

分别采用扩展Kalman滤波方法和本文方法（c=3）进行滤波，取滤波初始值X0=101，误差方差初始值P0=100。对系统进行500次蒙特卡洛仿真模拟，分别求得本文方法与线性Kalman滤波的均方根误差如图2所示，均方根误差的均值如表2所示。由图2与表2可以得到与前一算例相同的结论。

图2 本文方法与扩展Kalman滤波均方根误差比较Fig.2 RMSEs comparison of proposed method and EKF

表2 本文方法与扩展Kalman滤波均方根误差均值比较Table 2 RMSE means comparison of proposed method and EKF

4 结 论

本文提出的自识别自校准Kalman滤波方法，能够自动识别、估计并补偿状态方程中的未知输入（系统误差），有效提高滤波精度。文中分别对线性系统和非线性系统的自识别自校准滤波方法进行了详细讨论，给出了相应的公式和滤波步骤。

大量实例计算和仿真模拟表明：当有未知输入时，本文方法可以得到比传统Kalman滤波高得多的滤波精度；而当没有未知输入时，又能自动退回传统Kalman滤波。无论有无未知输入，工程上采用本文方法都优于传统Kalman滤波。