基于状态转移图的启发式深空探测器任务规划方法

金 颢，徐 瑞，崔平远，朱圣英

（1.北京理工大学深空探测技术研究所，北京 100081；2.深空自主导航与控制工业和信息化部重点实验室，北京 100081）

引 言

深空探测器自主任务规划技术是解决远距离探测器自主运行问题的一项关键技术[1]。由于探测器系统功能复杂以及外界环境不确定等特性，经典的规划技术很难直接应用到深空探测器任务规划中。探测器在轨运行过程中，需要具备能够对一系列科学目标进行规划的能力，即根据空间环境的感知及探测器本身的能力和状态，运用自主规划技术在约束和资源模型的基础上进行推理，生成一组有序的活动序列。同时，当深空探测器面临执行长期任务的挑战时，复杂和动态的外部环境会成为实现任务目标的阻碍[2-3]。这些都需要可靠的自主规划方法，以避免在缺乏对环境充分认知的情况下做出导致任务失败的决策。

深空探测器自主任务规划技术的研究和发展主要具有如下几方面的意义：①系统的自主性可使深空探测器在整个任务过程中减少地面干预，从而降低航天任务费用以及对航天网络的需求；②系统自身具备自主能力，可以进一步应对空间任务中的不确定性，增加任务的可靠性；③系统通过自主规划技术能够对各种资源进行合理分配和利用，提高任务的科学回报。

可扩展的通用远程操作规划架构（Extensible Universal Remote Operations Planning Architecture，EUROPA）中，自主规划模型能够对明确的时间概念进行描述，算法使用基于约束的规划范式对问题进行求解[4]。但是，其核心的搜索算法采用深度优先的搜索方式，缺乏合适的搜索引导策略，会在一定程度上影响规划的效率。“罗塞塔”任务中，探测器首次实现了与彗星的交会并最终成功登陆彗星。在任务执行周期内，探测器使用科学规划（Master Science Plan，MSP）软件制定的观测方案，保证了在动态外部环境中科学任务目标的成功实现[5-6]。由于探测器长时间处于未知且动态变化的环境中，MSP更注重制定灵活的策略来保障探测器的安全性，从而在算法搜索技术方面并未有太过深入的研究。王丹等研究了载人航天器上自主任务规划飞行程序的设计[7]；王晓晖等对深空探测器的约束简化与动态不确定因素进行了研究[8]。但在实际飞行过程中，探测器复杂的系统功能及科学任务突发性对任务规划技术提出了更高的要求，使得寻求一种更有效的规划搜索算法成为深空探测器自主任务规划中亟待解决的问题之一。

本文针对探测器系统并行及约束耦合的特点，采用基于时间线的问题建模方法。考虑系统内部约束复杂及状态切换的特性，建立状态转移图描述各子系统状态转移路径方案，设计了状态转移代价函数。然后，在转移图的基础上提出了规划节点启发式评估策略，对问题搜索空间进行削减，实现减少无效迭代次数，提高规划效率的目标。最后通过仿真实验，验证了启发式搜索算法的有效性。

1 时间线规划知识表示

为了便于对任务规划方法进行描述，首先给出时间线模型中的几个基本的概念。

定义1.状态变量是建模时对于系统知识的抽象结果，可定义为一个四元组：SV=。

其中：N为该状态变量的名称；V是该状态变量的取值空间，即状态变量的值域，为一个非空集合；T为该状态变量各取值之间的转换规则或约束；D表示该状态变量各取值的持续时间。

定义2.状态是状态变量在某一个时间点或某一时间区间上的取值，可用一个四元组进行表示：s=。

其中：Ns为该状态的名称；ts、te、d分别为该状态的起始时间、结束时间和持续时间，并且均表示为区间的形式，即ts=[s,s′]，te=[e,e′]，d=[d,d′]，用于应对执行过程中所可能出现的不确定性问题。

定义3.状态时间线用于表示系统状态变量在规划周期内取值（即状态）随时间的变化情况。每一条状态时间线都是系统在规划周期内的连续状态序列，即STL={s0,s1,…,sn-1,sn}。

2 状态转移代价计算方法

根据时间线知识表示方法，利用状态转移图来描述每个状态变量自身状态变化的方式以及实现这种状态改变所需要满足的条件。每个状态变量都有对应的一个转移图，图中的点为状态，点之间的边表示转移规则且每条边上标有状态转移需要满足的约束集合。例如，图1表示了在火星车测试用例中设备时间线的状态转移图。

图1 火星车设备时间线状态转移图Fig.1 A state transition graph for an Instrument timeline

状态转移图中任意2个状态s1和s2之间可能存在多条转移路径，计算所有路径的代价，并选择其中最低的代价作为状态s1到s2的转移代价cost(s1,s2)。同一时间线上两个状态间的转移代价由两部分构成：一部分为实际的状态转移次数所带来的代价；另一部分为每次转移的约束条件所引发的代价计算。不失一般性，在本文中每次状态转移所需代价为1，而转移约束的代价计算则是一个迭代的过程。

假设状态转移图中两相邻状态s1到s2的一个转移约束为状态s3，其中s1和s2属于时间线TL1，s3属于时间线TL2，时间线TL2上存在初始状态s0。则实现转移约束s3的代价即为时间线TL2上状态s0到s3的转移代价。同理，状态s0到s3的转移代价计算同样涉及转移次数代价和转移约束代价。如此反复迭代计算，最终能够得到实现转移约束s3的代价。而状态s1到s2转移约束代价为实现其转移约束集合中所有转移约束的代价和。计算出状态转移图中每两个相邻状态之间的转移代价后，则任意两状态之间的转移代价可由转移路径上所有相邻状态的转移代价求和得到。

图2 状态转移代价计算Fig.2 The procedure of compute-cost algorithm

计算转移图中任意两状态之间转移代价的算法如图2所示。针对上述状态转移代价计算方法，本文设计了基于状态转移图的启发式任务规划算法，能够在合理描述实际物理系统的同时，较为高效地实现问题规划。

3 基于状态转移图的启发式规划算法

深空探测器具有多子系统并行、运行约束复杂等特点，状态空间搜索会导致搜索空间指数爆炸。本文采用规划空间搜索方法，针对转移图代价计算特点形成启发式评价策略。规划空间搜索是搜索缺陷、挑选缺陷和解决缺陷3部分反复迭代的过程。每迭代一步需要进行一次约束传播检测，验证规划操作的合理性，并在必要时可以进行回溯，直到搜索出规划问题的一个可行解。

状态转移图能够对每个状态变量内部的转移规则进行描述，从而状态转移代价计算较经典规划的启发式而言更适合于时间线描述框架。在规划过程中，规划器不断实例化目标状态g∈G到当前部分规划，并将g的约束作为子目标加入目标集合G{g}，直到目标集合为空时，算法就找到了该问题的一个规划解。目标g通常存在析取约束集，即当前部分规划存在多个可扩展候选节点，使用状态转移代价计算能够对搜索过程中规划节点的展开进行评价，删除不必要的目标约束集合，实现搜索空间剪枝，加快搜索效率的目的。

假设状态s属于目标g的一个候选约束集合，则实例化s到当前部分规划的代价计算存在2类情况。

1）将状态s与时间线TL上另一满足约束的状态s'相融合，即

2）在时间线TL上添加状态s

第1类情况通过状态融合实现目标约束，由于对当前部分规划不作任何改变，所以代价为0。第2类情况需要对当前时间线上的状态分布进行改变，所以需要计算新的转移代价进行评估。在搜索过程中，每次迭代都伴随着目标集合的更新，动态计算目标代价会带来大量的计算耗时。而问题的初始状态集合在规划迭代的过程中不发生任何变化。从而选用时间线TL上的初始状态s0进行第2类情况的代价计算，将初始状态到状态s的转移代价作为添加状态s的评价值。实例化状态s的代价计算为

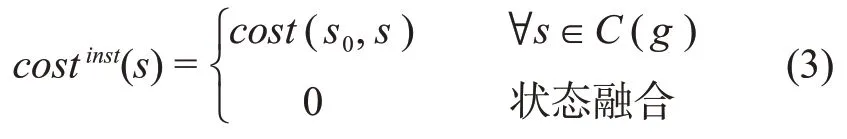
则实现目标g该候选约束集合的代价为

通过对目标g不同候选约束集合的代价进行计算，最终选择代价最低的约束集作为下一步要实现的子目标集加入到目标集合中，完成对规划节点的扩展。通过转移图，每条时间线能够找到多条由初始状态到目标状态的转移路径，而启发式对所有可能的转移路径进行评价并挑选出转移代价最低的路径作为下一次迭代的输入。

本文的规划算法采用规划空间搜索的形式，在其架构的基础上，根据状态转移图的定义和结构特点，同时考虑上述启发式搜索策略，设计了图3所示的基于状态转移图的启发式规划算法。该算法能够有效地减少由于节点扩展不合理引发的节点回溯，提高算法的效率。

图3 启发式规划算法Fig.3 Heuristic planning algorithm

4 仿真计算结果及分析

为了验证算法的有效性，建立了一个描述火星车领域的模型，并采用本文提出的算法进行了仿真验证。通过与EUROPA2算法仿真结果进行对比，验证了该算法能够有效提高规划搜索的效率。

本文在火星车领域中构建了10个测试用例。火星车上携带了采样设备对火星土壤进行采样，并置入自身的质谱仪中对土壤成分进行分析。同时火星车上还备有相机实现对火星表面地形数据收集。在该测试场景中，火星车模型总共需要对11个状态及资源时间线进行建模，包括：采样设备、电池电量、数据存储及相机等。并且需要对状态同步约束、变量约束及资源约束进行描述，例如通信时同样需要姿态系统保证一定的指向，状态消耗能源的总和不能超过能源最大值等。

考虑上述建模方法和约束形式，该模型包括9个设备或子系统（表1）。各并行子系统或设备间约束相互耦合，共包含32个状态模型和48个约束关系。

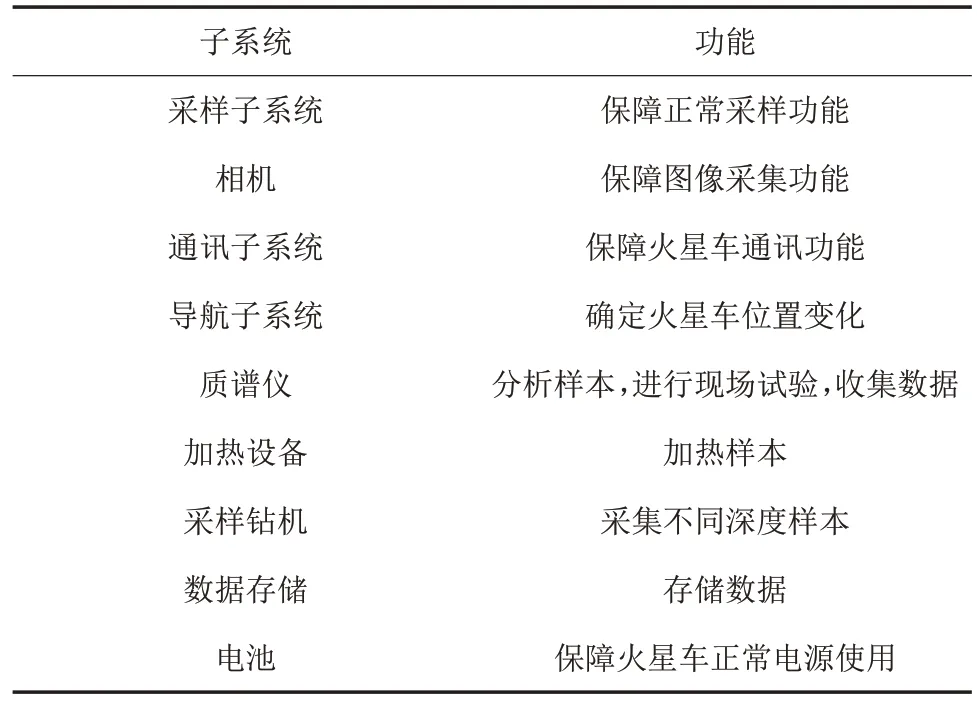
表1 火星车领域模型Table 1 Summary of subsystems in Mars Rover domain

本文选取深空探测器领域中10个不同的问题进行了仿真测试，结果如图4～6所示。由于测试问题按序号顺序所包含的目标的数量是逐渐增多的，故两种算法的计算处理时间是递增的。并且，为避免出现偶然性，本文的测试用例中对每个问题统计其10次计算的平均值。

通过仿真结果可以看出：状态转移启发式算法的处理时间要低于采用EUROPA2算法的处理时间，且曲线的走势表明，随着问题所含任务目标数量的增加，EUROPA2算法运行时间的增长速率要高于后者。对于复杂任务而言，更多的任务目标要求规划器能够在搜索中做出更明智的决策。EUROPA2在搜索中采用深度优先策略，虽然保证了算法的完全性，但是对无效节点过多的扩展大大降低了搜索的效率（如图6所示）。

本文的启发式算法通过计算状态转移代价，完成对部分无效搜索节点的剪枝，既能够保证规划的准确性，又减少了不必要的回溯步数。如图5所示，启发式算法所需的规划步数全部低于EUROPA2求解所用步数，进一步证明了本文设计的启发式能够有效地保证规划的效率，提高问题求解的速度。

图4 运行时间结果曲线Fig.4 Computational results of runtime curves

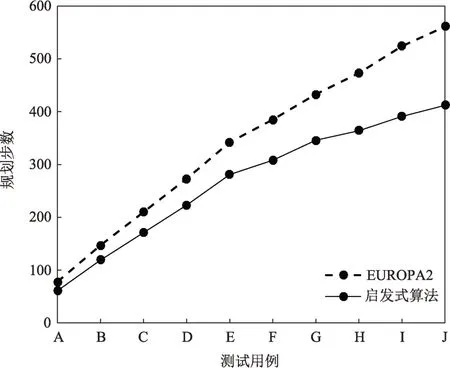
图5 规划步数结果曲线Fig.5 Computational results of planning steps

图6 扩展节点结果曲线图Fig.6 Experimental results on explored plans

5 结 论

本文针对深空探测器任务规划中多系统并行、功能复杂且约束耦合等特点，采用时间线知识表示框架对系统及任务进行建模。通过分析时间线的结构特点，引入状态转移图结构，并设计了状态转移代价计算方法。结合规划空间搜索策略，提出了基于状态转移图的启发式规划算法，实现了削减搜索空间、优化规划搜索的目的。最后选用EUROPA2算法进行对比实验，并针对火星车任务规划系统进行建模仿真，仿真结果验证了本文的启发式算法能够有效地对搜索空间进行剪枝，减少不必要的规划步数，提高了任务规划的效率。