月面上升的轨迹优化与参数分析

张 磊

（航天东方红卫星有限公司，北京 100094）

引 言

我国将在2020年左右实施月球采样返回任务，月面上升是任务的关键环节之一。月面上升是上升器从月面着陆器平台起飞，经过连续动力飞行进入预定轨道的过程，可大致分为点火起飞、垂直上升、快速姿态调整、制导入轨等阶段[1-2]。研究上升轨迹优化及总体参数对燃料消耗的影响对任务分析具有重要意义。

月面上升的轨迹优化是以上升过程中燃料消耗最少为性能指标的最优控制问题，可将其通过间接法转化为两点边值问题或通过直接法转化为非线性规划问题进行求解[3-5]。李鑫等[6]采用粒子群算法、马克茂等[7]采用初值预估和向前扫描法对上升器平面上升轨迹优化的两点边值问题进行求解，Hull等[8-9]基于简化的月面上升运动模型利用间接法推导了燃料次优制导律，通过在各个采样点上依次求解得到上升轨迹，适合在线计算。相比间接法，直接法对轨迹优化问题的转化使得求解过程在鲁棒性和通用性上更具优势。伪谱法是近些年发展起来的一种全局配点的直接法，其以全局插值多项式为基函数近似整个时间历程的状态变量和控制变量，能够以较少的配点获得较高的精度[10]，在最优控制问题上得到广泛应用[11-14]。

本文建立了上升器月面上升运动模型，采用基于重心Lagrange插值的Gauss伪谱法将月面上升轨迹优化转化为非线性规划问题，进而采用序列二次规划进行求解。基于上述优化过程，对影响燃料消耗的总体参数：初始推重比、目标轨道高度、目标轨道倾角等进行了研究。考虑上升器延后或提前起飞的情况，提出了上升偏航、升交点经度调整、倾角调整3种方案，并从燃料消耗的角度分析了它们的适用范围。

1 月面上升运动模型

定义起飞点惯性坐标系Sa，原点a位于起飞点，xa在当地水平面内指向飞行方向，其与北向夹角χa为起飞方位角（东偏为正），ya沿当地铅垂方向向上，xaya平面为名义上升平面，如图1所示。

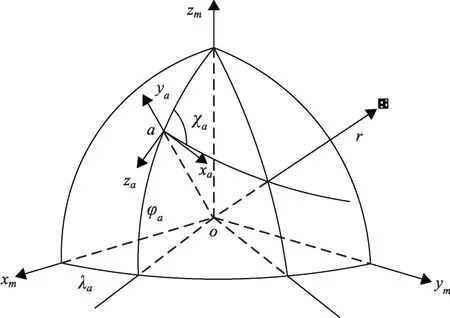
图1 起飞点惯性坐标系示意图Fig.1 Illustration of the launch inertial coordinate system

月面上升运动方程在月心赤道固连系Sm为

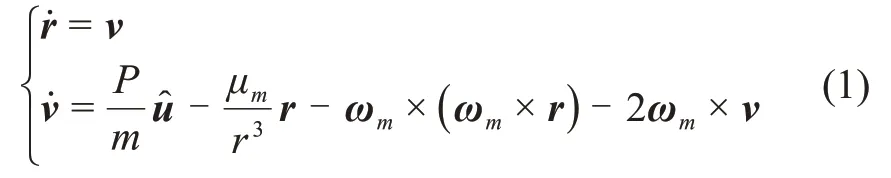
其中：r、v分别为上升器相对Sm系的位置矢量、速度矢量；μm、ωm分别为月球引力常数、自转角速度；m为上升器质量，m=m0-，m0为上升器初始质量；为发动机秒消耗量；P为发动机推力；为推力方向。

在Sm系中的坐标分量为

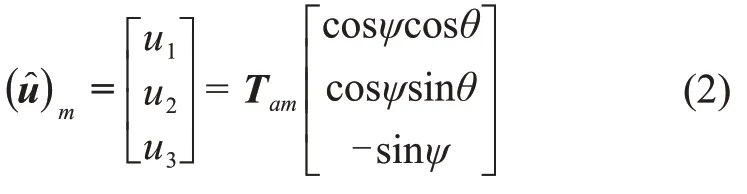
其中：θ、ψ分别为相对Sa系推力俯仰角（向上为正）、推力偏航角（向右为正）确定。

起飞点在惯性坐标系中的推力方位示意图如图2所示，Sm系到Sa系的坐标转换矩阵Tam为

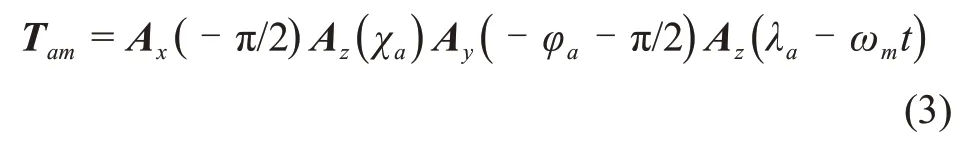
其中：Ax(·)、Ay(·)、Az(·)分别为绕x轴、y轴、z轴的单位旋转矩阵；λa、φa分别为起飞点经度、纬度；ωm为月球自转角速率；t为飞行时间。

图2 起飞点惯性坐标系中的推力方位示意图Fig.2 Thrust direction at the launch inertial coordinate system

在分析与入轨方位无关的参数（如高度、初始推重比等）时，由于月球自转速度较慢，简化考虑即可忽略月球自转，此时上升器在名义上升平面内运动，推力偏航角ψ为0。月面上升平面示意图如图3所示，平面月面上升平面运动模型为

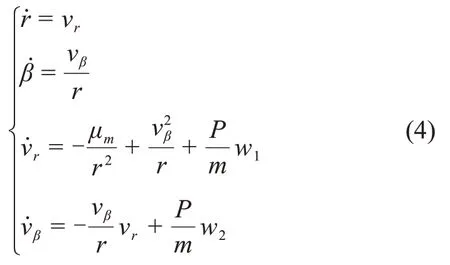
其中：r为上升器月心距；β为上升器与起飞点月心夹角；vr为上升器径向速度分量；vβ为上升器横向速度分量（沿当地水平）；w1=sinη，w2=cosη，η为相对当地水平的相对推力俯仰角（向上为正），η=θ+β。

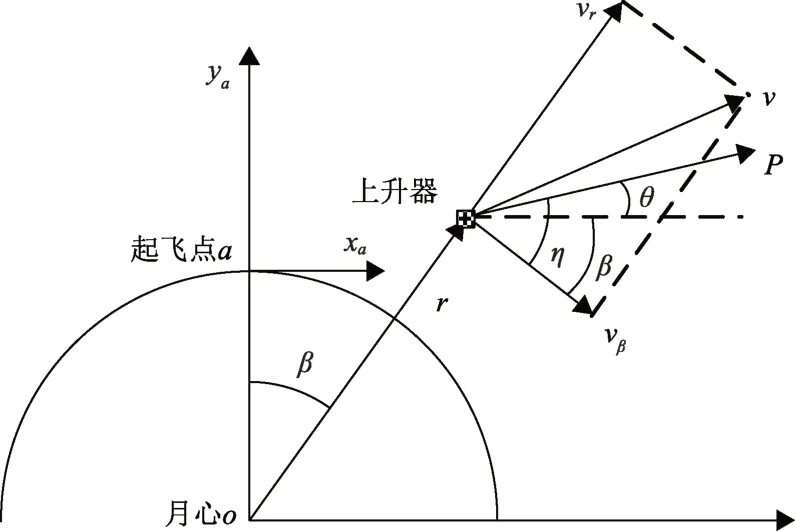
图3月面上升平面运动示意图Fig.3 Illustration of planar lunar ascent

在轨迹优化中，为克服由状态变量量级不同造成的有效数位丢失，保证状态方程积分精度，同时提高收敛效率，通常对状态方程进行无量纲化处理。

引入无量纲因子

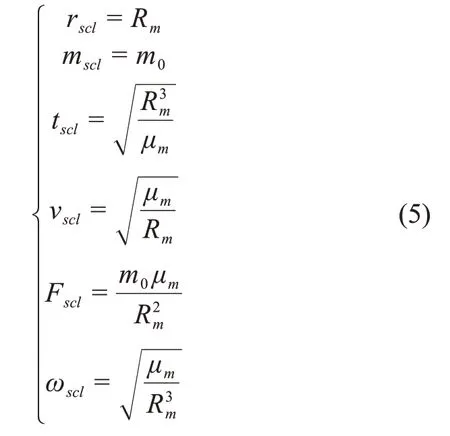
其中：Rm为月球半径；μm为月球引力常数。

则月面上升运动模型式（1）、式（4）的无量纲形式分别为

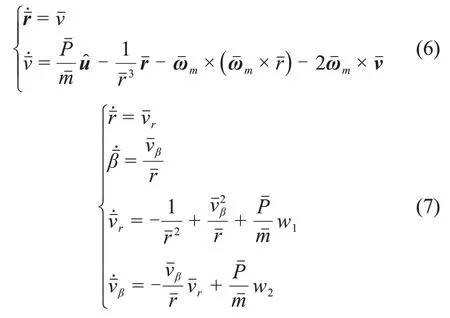
此外，还需补充推进方程式为

其中：为燃料秒耗量；Isp为发动机比冲（单位：s）；ge为地球表面重力加速度，上升器采用常值推力发动机，秒耗量为常值。

2 月面上升轨迹优化问题求解

2.1 问题描述

月面上升轨迹优化是终端时间tf未定的最优控制问题，将燃料消耗最少的性能指标等价为入轨质量最大，由于秒耗量为常值，性能指标也可取为tf最小。

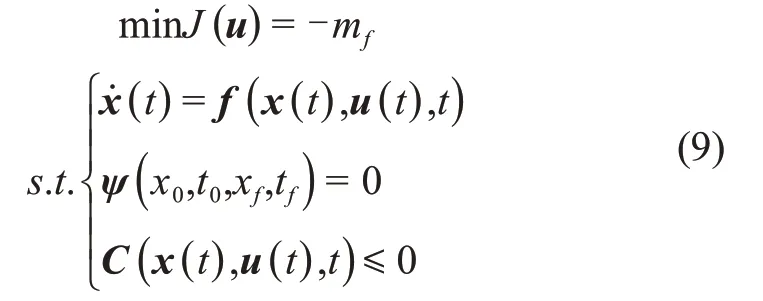
其中：x、u分别为状态变量（位置、速度、质量）、控制变量（推力俯仰角、推力偏航角）。

约束条件分别为状态方程、边界条件和路径约束。状态方程即运动方程及推进方程。边界约束由初始状态和入轨参数确定，初始状态r0由起飞点确定，v0=0，m0为给定值，入轨参数根据分析需要选择目标轨道近（远）地点高度、倾角、升交点赤经等，可根据轨道方程由终端状态计算得到。路径约束考虑对推力俯仰角及推力偏航角取值范围的约束。

2.2 Gauss伪谱法

伪谱法是一种全局配点法，利用全局插值多项式将连续最优控制问题转化为以配点处状态变量和控制变量为待求参数的非线性规划问题。

Gauss伪谱法采用N阶Legendre-Gauss点（N阶Legendre多项式的N个零点）以及τ0=-1作为配点，τj∈[-1,1)j=0,…,N。因此，首先通过式（10）将原问题的时间区间t∈[t0,tf)转换到Lagrange插值多项式的定义区间τ∈[-1,1)上。

根据配点处的状态变量、控制变量，以Lagrange插值多项式作为基函数，可构造状态变量、控制变量的全局插值多项式，随后通过微分求导将状态方程转化为在配点上的等式约束，但Gauss伪谱法的配点不含1，因此，在终端不能按上述方式将状态方程转化为等式约束，而利用Gauss求积公式得到终端状态的等式约束。边界条件、路径约束可直接根据配点及边界上的状态量、控制量转化为相应的等式或不等式约束。式（9）定义的月面上升轨迹优化问题是典型的终端型最优控制问题，性能指标直接根据终端状态确定。通过以上步骤，就可以得到以配点上状态变量X(τk)k=0,…,N、控制变量U(τk)k=1,…,N，终端状态变量X(1)以及终端时间tf为待求参数的非线性规划问题为

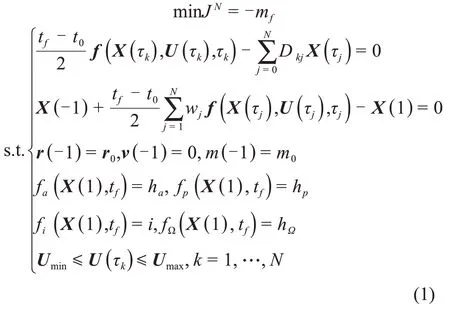
其中：fa、fp、fi、fΩ分别指根据终端状态计算入轨远月点高度、近月点高度、倾角、升交点赤经；wj为Legendre-Gauss点上的Gauss求积系数。

Dkj为微分矩阵的元素

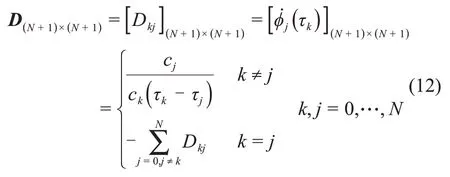
其中：φj(τ)为重心Lagrange插值多项式。

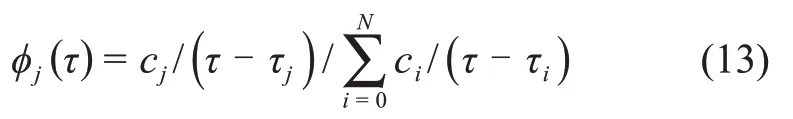
其中：cj为重心权。

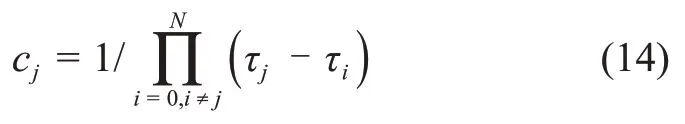
相比一般的Lagrange插值多项式，在配点数量较大时采用重心Lagrange插值多项式具有极好的数值稳定性[15]。

序列二次规划[16]是目前应用最为广泛、最有效的求解非线性规划问题的算法之一，Matlab中的fmincon函数使用的即是该算法。本文采用fmincon函数求解式（11）所示的非线性规划问题。

2.3 轨迹优化算例

上升器延后一圈起飞，降段入轨，目标轨道近月点高度15 km、远月点高度100 km、轨道倾角20°、升交点经度251.19°，月面起飞点位置15°N、25°E，起飞方位角103.51°，上升器初始质量800 kg，发动机推力5 500 N，比冲300 s。由仿真结果可知，上升器飞行时间192.75 s，消耗燃料360.63 kg。图4～5显示推力控制角与时间基本呈线性关系，而它们的初始值则表明上升器必须通过快速姿态调整从垂直起飞姿态（推力偏航角0°、推力俯仰角90°）建立制导入轨初始姿态。图6上升器飞行高度随时间变化的曲线，入轨高度15.06 km。

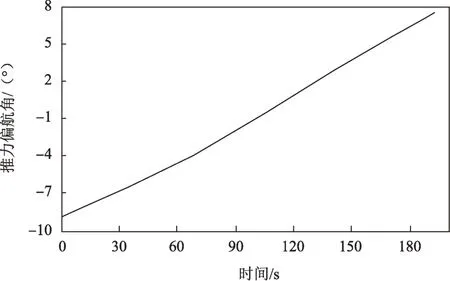
图4 推力偏航角随时间变化曲线Fig.4 Time history plot of thrust yaw angle

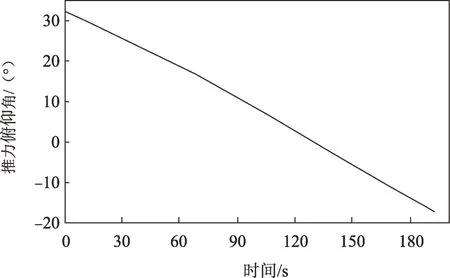
图5 推力俯仰角随时间变化曲线Fig.5 Time history plot of thrust pitch angle

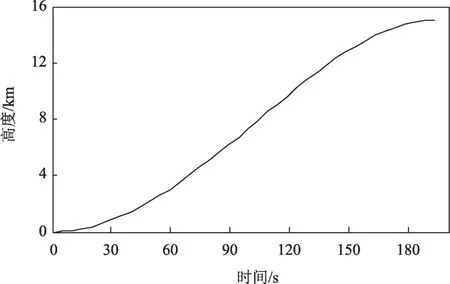
图6 飞行高度随时间变化曲线Fig.6 Time history plot of altitude

3 月面上升的参数分析

通过月面上升轨迹优化寻求最佳的推力控制过程以减少燃料消耗，一些总体参数及起飞时机对上升过程的燃料消耗也具有重要影响，通过比较这些参数在不同取值下的轨迹优化结果可以对其进行分析研究，这对于任务分析尤为重要。以等效速度增量Δv描述上升过程的燃料消耗Δm为

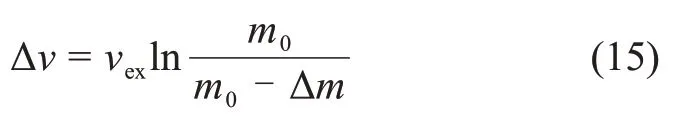
其中：vex为发动机排气速度，vex=Ispge；Δm为燃料消耗。

3.1 初始推重比的影响

初始推重比为

需要注意的是，这里的初始重量以地球表面重力加速度计算。采用月面上升平面运动模型式（8）研究初始推重比对燃料消耗的影响。上升器初始质量m0=800 kg，发动机比冲Isp=300 s，初始状态为上升器月面静止，目标轨道近月点高度15 km，远月点高度100 km，初始推重比对燃料消耗的影响如图7所示。

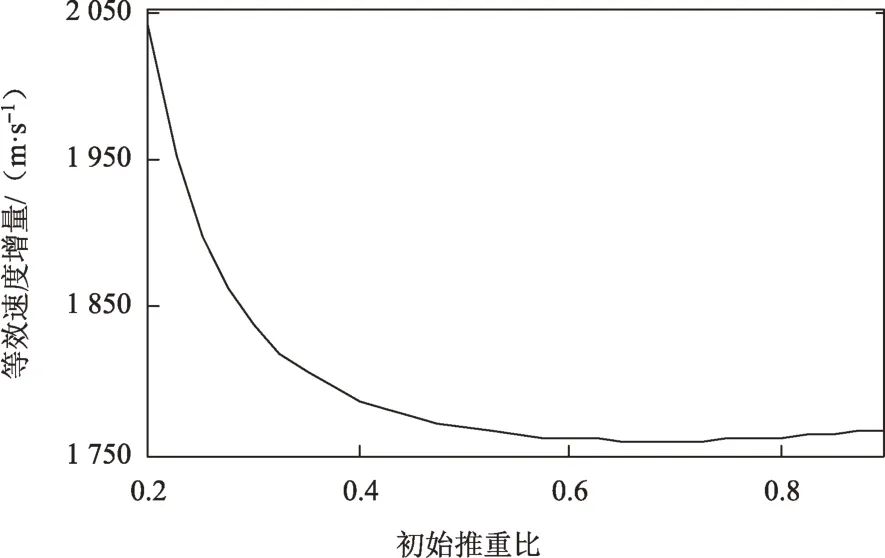
图7 初始推重比对燃料消耗的影响Fig.7 Fuel consumption vs.initial thrust/mass ratio

由图7可知，初始推重比存在一临界值使得燃料消耗最少，在当前设置的仿真条件下该值约为0.7，当初始推重比大于该值时，随初始推重比变大等效速度增量缓慢增加，当初始推重比小于该值时，随初始推重比减小等效速度增量呈指数上升。因此，在确定发动机推力及上升器总质量时应尽可能保证初始推重比在临界值附近。

3.2 目标轨道高度的影响

采用月面上升平面运动模型（8）研究目标轨道近月点高度及远月点高度对燃料消耗的影响。初始推重比为0.7，仿真结果如图7～8所示。

由图8和图9可知：近月点高度对等效速度增量的影响远大于远月点高度的影响，近月点高度从15 km 增加到75 km，等效速度增量从每10 km 增加10 m/s 到每10 km 增加40 m/s，而远月点高度每提高20 km等效速度增量仅增加约5 m/s。因此，在确定近月点高度时需考虑其对燃料消耗的影响，而远月点高度的确定应从调相轨道约束等方面进行分析，不必考虑燃料消耗。

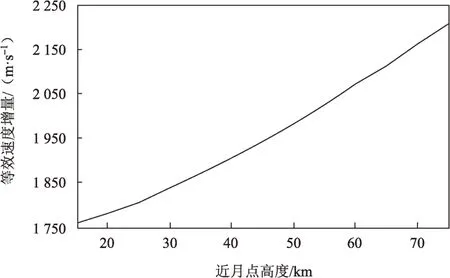
图8 近月点高度对燃料消耗的影响Fig.8 Fuel consumption vs.perilune altitude

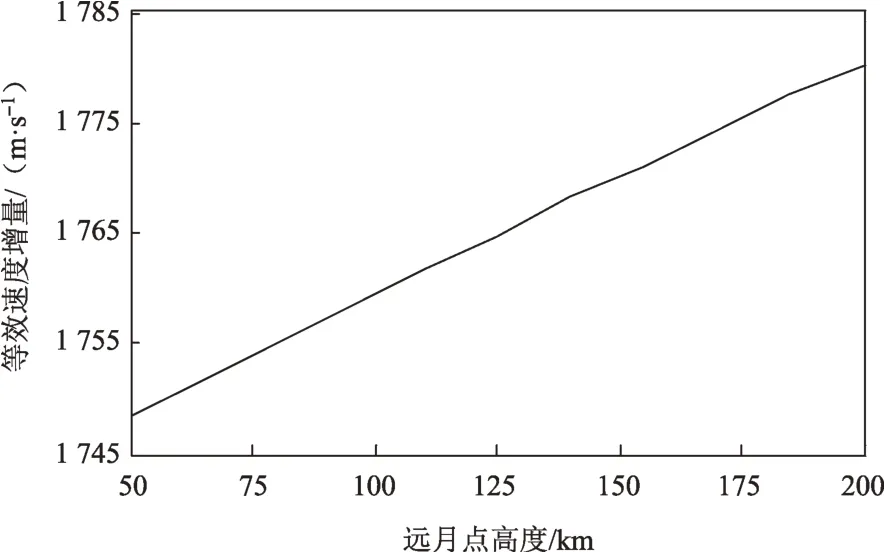
图9 远月点高度对燃料消耗的影响Fig.9 Fuel consumption vs.apolune altitude

3.3 目标轨道倾角的影响

采用月面上升运动模型（5）研究目标轨道倾角对燃料消耗的影响。上升器降段入轨，上升过程无推力偏航，月面起飞点位置15°N、25°E，目标轨道近月点高度、远月点高度分别为15 km、100 km，目标轨道倾角对燃料消耗的影响仿真结果如图10所示。

图10 目标轨道倾角对燃料消耗的影响Fig.10 Fuel consumption vs.orbit inclination

如图10知：由于月球自转的影响，等效速度增量随轨道倾角增大而增加，即东向起飞比西向起飞节省燃料，但月球自转角速率非常缓慢，使得等效速度增量增加幅度很小，160°倾角仅比20°倾角增加约9 m/s，多消耗燃料小于1.5 kg，远小于地球上的量级。

3.4 起飞时机的影响

着陆点随月球自转进入轨道器停泊轨道面时，上升器可采用共面上升方式，不进行偏航机动，记此时的停泊轨道为0圈轨道。当需要上升器延后或提前起飞时，为使其进入与轨道器共面的轨道，可采用以下3种方案。

1）上升偏航，上升器在飞行过程中进行偏航机动，直接进入与轨道器共面的初始轨道，其相比共面上升增加的速度增量Δvy可根据轨迹优化结果计算。

2）升交点调整，如图11所示，上升器以共面上升方式飞行，使上升器初始轨道与轨道器停泊轨道的倾角相同而升交点不同，轨道器在圆形停泊轨道上通过调整升交点经度使二者共面，所需速度增量ΔvΩ为

其中：vpo为停泊轨道速度；υ为两轨道面夹角。

其中：ipo为停泊轨道倾角，n为延后或提前起飞的圈数，延后起飞为正，提前起飞为负；ΔΩm为停泊轨道每圈升交点经度的变化。

其中：Tpo为停泊轨道周期；ωm为月球自转角速率。

图11 轨道调整方案示意图Fig.11 Illustration of orbit maneuver

3）倾角调整，上升器以共面上升方式飞行，使上升器初始轨道与轨道器停泊轨道的升交点相同而倾角不同，轨道器在圆形停泊轨道上通过调整倾角使二者共面，如图11所示，所需速度增量Δvi由式（20）计算

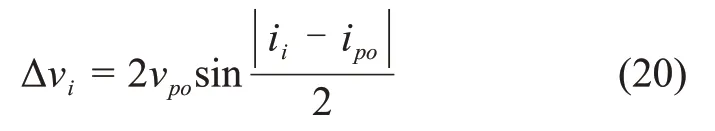
其中：ii为上升器轨道倾角。

将停泊轨道升交点经度作为终端约束通过轨迹优化可确定ii的数值，也可由式（21）进行粗略计算。

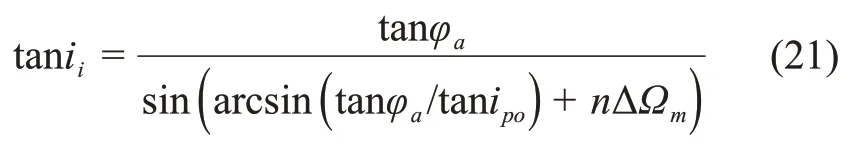
其中：φa为起飞点纬度。

轨道器停泊轨道高度100 km、倾角20°，上升器目标轨道近月点高度15 km、远月点高度100 km。根据轨迹优化结果可知，共面上升起飞方位角103.51°，0圈轨道升交点经度252.36°，上升过程等效速度增量1 755.06 m/s。则上述3种方案相对共面上升增加的额外速度增量Δvy、ΔvΩ、Δvi如图12所示，当延后或提前起飞时间小于2圈时，上升偏航方案的燃料消耗小于其它两种方案，当延后超过2圈时，可采用升交点调整或倾角调整方案，当提前超过2圈时，宜采用倾角调整方案。

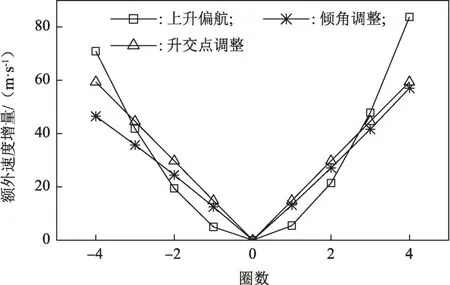
图12 起飞时机对燃料消耗的影响Fig.12 Fuel consumption vs.ascent window

4 结 论

针对燃耗最优的月面上升轨迹优化问题，采用基于重心Lagrange插值的Gauss伪谱法及序列二次规划进行求解。通过参数分析的研究指出，上升器初始推重比、目标轨道近月点高度对燃耗影响较大，而目标轨道远月点高度、倾角的影响则小得多。针对非共面上升，提出上升器上升偏航、轨道器倾角调整和升交点调整3种方案，当目标轨道相对共面上升轨道偏差较小时，宜通过上升偏航进入目标轨道，对偏差较大的情况，宜按照后2种方案通过调整目标轨道尽量满足共面上升条件。