以一个平面几何定理为例谈数学问题的提出

摘要：以基于切线长定理编制的一些问题为例，谈数学问题提出的一些基本策略和方法：稍微增加图形的复杂性，逆向思考条件和结论，将两个或多个结果结合起来，推广先前的结果，利用先前结论的对称性命题。

关键词：切线长定理数学问题提出问题

许多数学家和数学教育家都认为“提出数学问题”是一种重要的数学活动，学生应该尽早获得“提出数学问题”的经验。Kilpatrick（1987）曾撰文给出过一些数学问题的提出策略，如联结（Association）、类比、一般化、反驳、换位思维法和观念组合法等。运用这些策略可以帮助学生提出更多的数学问题。Brown等人（1983）曾在其专著《提出问题的艺术》中给出过一个提出问题的很有用的方法——对原问题的条件和限定进行思考而自由改变，即所谓的“否定假设法”（“whatifnot”策略：如果它不是这样的，那又可能是什么呢？）。这是产生新问题的非常有效的方法。Lavy等人（2003）曾基于一个复杂的立体几何问题，要求被试运用“否定假设法”来提出问题。结果显示：学生能够提出大量的数学问题，包括数值改变问题、变量改变问题以及把问题转化為证明问题等。

笔者（2015）曾在J.N.Contreras（2003）的基础上给出过一个提出数学问题的模型，见图1。这个模型无疑对一线教师指导学生提出数学问题具有一定的参考价值。此后，笔者（2015）从课堂教学中的一道错题出发论述了数学问题的提出，（2016）又以一道简单的平面几何问题为例论述了数学教学中培养学生提出问题能力的一点体会。

本文将以一个典型的平面几何定理为例，谈谈数学问题提出的一些基本策略和方法。这个定理是：如图2，从⊙O外一点P引⊙O的两条切线PA、PB，则PA=PB。这个定理的证明很简单：一种方法是证明△PAO≌△PBO;另一种方法是由弦切角定理得∠PAB=∠PBA=m12AB，则△APB是等腰三角形，故PA=PB。

我们当然可以编制各种各样的测试学生理解这个定理的数值练习（甚至一些是很好的练习）。但是，我们更喜欢几何问题而不是算术问题。换句话说，我们希望学生使用相关定理证明相关结果。为此，我们可以采用如下策略和方法提出问题。

一、稍微增加图形的复杂性

我们可以在⊙O上引入另一条切线CD（如图3）。这样，就得到两个不同难度层级的问题（即问题1和问题2）。

问题1如图3，PA、PB、CD是⊙O的三条切线，切点分别为A、B、Q，证明：PA+PB=PD+DC+CP。

问题2如图3，PA、PB是⊙O的两条切线，Q为劣弧AB上的一点，若CD是以点Q为切点的⊙O的切线，试证明：△PCD的周长是恒定的。

我们还可以在⊙O上添加另一条位置不同的切线QR（如图4）。这样，立刻又得到一个新问题（即问题3）。

问题3如图4，A、B和C分别是⊙O三条切线PQ、PR和QR上的切点，求证：PA+QC+RB=AQ+CR+BP。

二、逆向思考条件和结论

之前，我们是知道直线和圆相切，确定线段的相等关系。现在，我们可以反过来：知道线段的相等关系，确定直线和圆相切。这样，又可以得到一个新问题（即问题4）。

问题4在任意△PQR的边上构造点X、Y和Z，使得PX=PZ，QX=QY和RY=RZ。

解决办法是作出△PQR的内切圆。

三、将两个或多个结果结合起来

结合图3和图4，我们又可以获得问题5。

问题5如图5，已知△PQR和六边形DEFGHI都外切于⊙O，求证：△PQR的周长等于△PDI、△QFE和△RHG的周长之和。

问题5的证明是三次直接应用问题1的结论，然后相加。

四、推广先前的结果

例如，我们可以将问题3推广到一个圆内切于四边形的情况：如图6，四边形PQRS外切于⊙O，求证：PW+QX+RY+SZ=WQ+XR+YS+ZP。还可以进一步推广到一个圆内切于n边形的情况，得到类似的结论。

当然，推广问题有时会遇到一些麻烦。比如，将问题4推广到四边形的情况：在四边形PQRS的边上找出点W、X、Y和Z，使得PZ=PW，QW=QX，RX=RY和SY=SZ。但是，图7显示了这个问题并不总是能够解决。

五、再次逆向思考条件和结论

例如，我们将问题6的条件和结果互换，又可以得到一个新问题（即问题7）。

问题7求证：如果一个凸四边形两组对边的长度之和相等，那么这个凸四边形一定有一个内切圆。

这个结论很有意思，和“两组对角的大小之和相等的四边形一定有外接圆（即对角互补的四边形是圆内接四边形）”有一种“对称”的美。

六、再次将两个或多个结果结合起来

结合图4和图8、图9，我们可以联想到：四边形可以被对角线分割成两个三角形，如果两个圆分别内切于这两个三角形呢？于是，我们可以从特殊到一般提出两个新的问题（即问题8和问题9）。

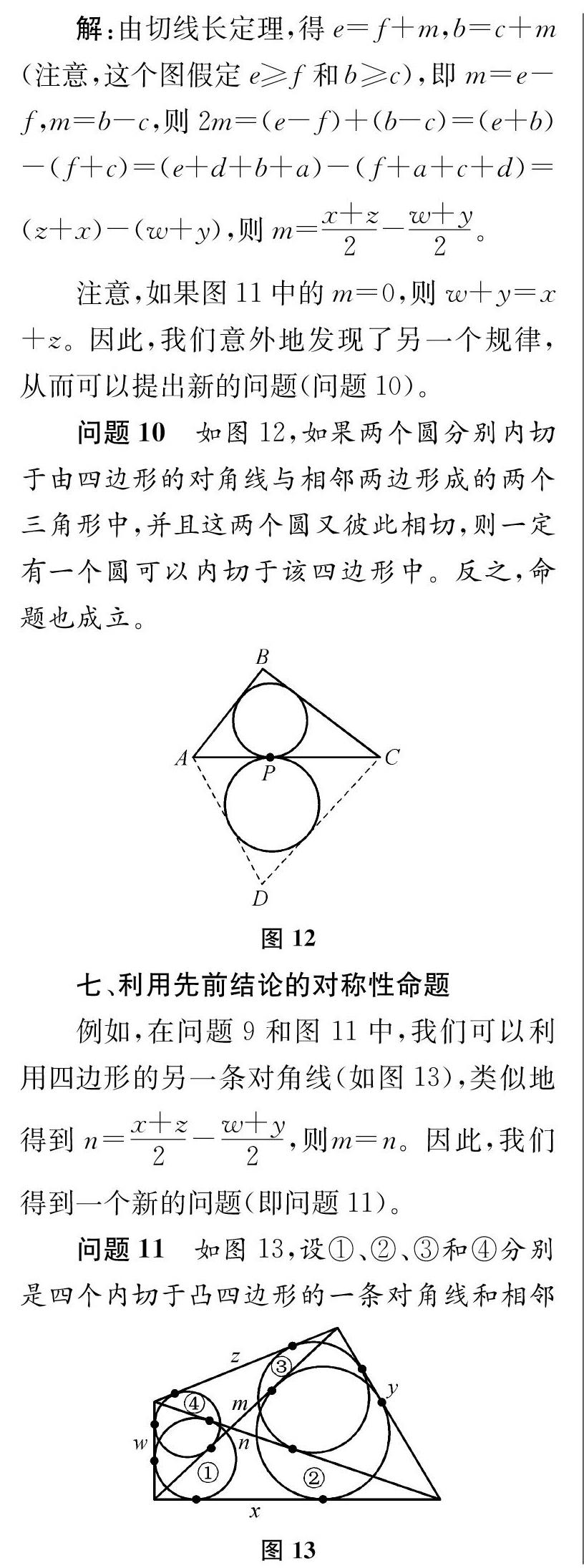
七、利用先前结论的对称性命题

两边构成的三角形的相互有重叠的圆。设m和n分别为这四个圆与对角线相切的切点之间对角线上的线段长，求证：m=n。

如上，所提出的问题越来越复杂。因此，提问者可能希望通过其他角度提出新的问题。例如，还可以从如下方向考虑能否提出新的问题：（1）非凸四边形;（2）凸的或非凸的五边形、六边形等;（3）球和多面体;（4）三角形的内角平分线;（5）圆的割线定理。

在提出这些问题时，细心的读者可能会注意到：我们使用了一些相同的技术，如特殊化、一般化、相关的问题、逆命题、对称、先前的结果、意外的结果等。可见，提出数学问题还是有一些规律和基本的策略、方法可以遵循的。

参考文献：

[1] Kilpatrick，J.Problem formulating：Where do good problems come from？[C]//A.H.Schoenfeld （Ed.）.Cognitive science and mathematics education.Hillsdale，NJ：Lawrence Erlbaum，1987.

[2] Brown，S.I.，Marion，I.W.The art of problem posing[M].Hilldate，NJ： Lawrence Erlbaum Assoc，1983.

[3] Lavy，I.，Bershadsky，I.Problem Posing via “whatifnot” strategy in solid geometrya case study[J].Journal of Mathematics Behavior，2003（22）.

[4] 徐彦辉.数学解题后的“回顾与反思”与数学问题的提出[J].数学教育学报，2015（1）.

[5] 徐彦辉.从课堂教学中的一道错题出发谈数学问题的提出[J].数学传播，2015（3）.

[6] 徐彦辉.培养学生提出问题能力的实践体会——以《证明一》复习课教学为例[J].教育研究与评论（中学教育教学），2016（11）.