纵向延展：往学科纵深处探秘——《三角形的内角和》一课的延展式学习

宗理

摘要：《三角形的内角和》一课的纵向延展，基于学生有了演绎推理的萌芽，旨在让学生充分地经历演绎推理的过程，培养初步的演绎推理能力。教学时，要遵循学生的认知规律，准确定位;要提供支架、搭建平台，助力学生在数学纵深处的探秘，促进学生数学活动经验的提升。

关键词：延展式数学学习纵向延展三角形的内角和

一、课前慎思

苏教版小学数学四年级下册《三角形的内角和》一课，主要通过量和算、撕和拼、折和拼等具体操作，归纳出三角形的内角和是180°。课堂上，量和算的学生，得到了178°、181°、175°等度数;而撕和拼、折和拼的学生，有的拼出来的不像个平角，有的缝隙总对不上。虽然有教师的解释“量、拼会存在一定的误差”，总不免让之前说好的“验证三角形的内角和为180°”显得有点儿牵强、不可信。

这不，课后，几个学生不服气地围着我说：“老师，我有不同的方法证明三角形的内角和是180°……”“我也有方法，而且没有误差……”他们更多使用的是演绎推理证明的方法。

虽然，小学阶段，基于学生思维的基本特点——从以形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式，学生主要接触的是归纳推理，但是，既然他们有了演绎推理思维的萌芽，我们的教学为何要停止在归纳推理上？而且，有研究表明，10-11岁是儿童演绎推理快速发展的时期。于是，我决定第二天再上一节《三角形的内角和》的延展课，让学生充分地经历演绎推理的过程，培养初步的演绎推理能力。课前，布置学生想一想：还有没有其他的方法来证明三角形的内角和是180°？可以画画、写写、剪剪、拼拼。

二、教学过程

（一）回顾实验归纳

师 昨天的数学课上，我们通过哪些方法得到了三角形的内角和是180°的？

生通过测量三个角的度数，相加得到三角形的内角和是180°。

生还通过撕和拼的方法得到一个平角，通过折和拼的方法也得到了一个平角，得出三角形的内角和是180°。

师是的，昨天我们是通过实验的方法，得出了三角形的内角和是180°。可是下课的时候，有好几个小朋友围着我，跟我说他们还有其他的方法也能证明三角形的内角和是180°。你们找到了不同的方法来证明三角形的内角和是180°了吗？

（学生先小组内交流，再全班交流。）

[教学意图：回顾上一节课学习的三角形内角和的证明方法，帮助学生快速回忆操作、实验的过程，概括出这些都是归纳验证的方法。]

（二）演绎推理，步步推进

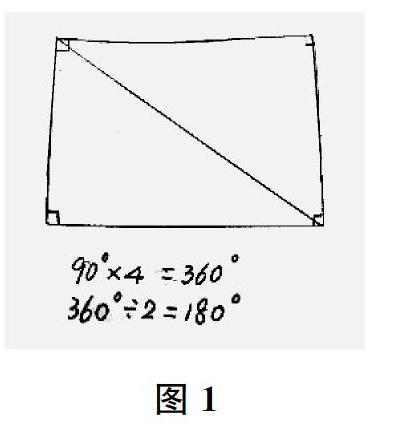
生（出示图1）我画了一个长方形，长方形的四个角都是直角，所以长方形的内角和是360°。然后画一条对角线，把长方形分成两个完全一样的三角形，那么一个三角形的内角和就是180°。

师（出示一个长方形纸片）你怎么确定对角线把长方形分成了两个完全一样的三角形？

生（取过老师手中的长方形纸片现场操作）我们沿着对角线把长方形剪开，然后把这两个三角形重叠在一起，发现完全一样。

（学生鼓掌。）

生这种方法只能说明直角三角形的内角和是180°，因为长方形沿对角线分成的两个三角形一定是直角三角形。还有锐角三角形和钝角三角形的内角和怎么办？

师那你有办法吗？

生我有办法。其实我们不一定要画长方形，画一个任意的四边形就可以了。（出示图2）我们总能用对角线把四边形分成两个三角形，你看这里就出现了钝角三角形和锐角三角形。四边形的内角和是360°，除以2是180°，三角形的内角和就是180°。

生我有疑问。你怎么知道你分成的两个三角形的内角和是一样的？只有一样才能用360°÷2呢。万一内角和一个大、一个小呢？

生我也有疑问。你怎么知道你画的四边形的内角和是360°的？

（被问的学生一时答不出话来。）

师虽然他的推理遭到了同学们的质疑，但也让我们明白了第一位同学为什么要在长方形里研究。

生因为长方形的四个角都是直角，内角和一定是360°;而且长方形的对角线一定是把長方形分成两个完全一样的直角三角形，那我们就确定了直角三角形的内角和一定是180°。

师你说得有理有据，一下子就让好多同学明白了一开始想到在长方形里研究原来还有这么多原因。其实，第二位同学的发言还提醒我们不能只考虑直角三角形的内角和，还要进一步研究锐角三角形和钝角三角形的。

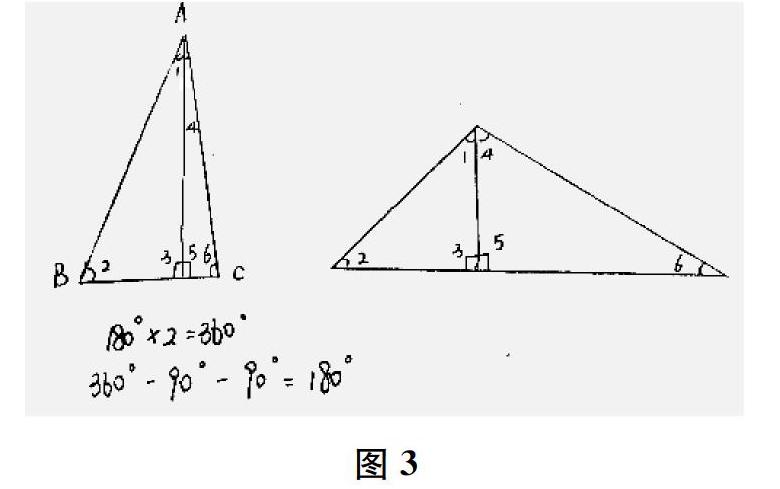
生我先画一个锐角三角形ABC，（出示图3）过A点作BC的高，这样就把锐角三角形分成了两个直角三角形。两个直角三角形的内角和是180°×2=360°，再减去∠3和∠5，所以锐角三角形的内角和=360°-90°-90°=180°。

师为什么要减去∠3和∠5？能说得再明白些吗？

生左边直角三角形的内角和是∠1+∠2+∠3=180°，右边直角三角形的内角和是∠4+∠5+∠6=180°，但是三角形ABC的内角和是∠1+∠4+∠2+∠6，∠3、∠5不是三角形ABC的内角，所以要减去两个直角，也就是两个90°。

师∠3是左边三角形的一个内角，∠5是右边三角形的一个内角，但它们不是三角形ABC的内角——内角不但要在图形的内部，而且还是由这个图形的边组成的。

生钝角三角形也是这样，先画一条高……

师刚才我们研究了锐角三角形和钝角三角形，它们的内角和都是 180°。还需不需要研究其他的锐角三角形和钝角三角形的内角和了？

生没有必要了，因为每个三角形都可以画高，都能把三角形分成两个直角三角形，都能得出内角和是180°。

师刚才的过程太巧妙了！我们先利用长方形证明了直角三角形的内角和是180°，然后把锐角三角形和钝角三角形都转化成直角三角形，从而证明了锐角三角形和钝角三角形的内角和也都是180°，最终得出了所有三角形的内角和是180°。

[教学意图：学生的演绎推理从长方形中的三角形开始，从直角三角形内角和的证明到锐角三角形和钝角三角形内角和的证明，虽然整个演绎推理的过程不是来自一名学生，是全体学生共享、交流的产物，但学生经历了一个完整而又严密的推理过程，在这个过程中，有肯定，有质疑，有反思，有共鸣，有思维上的满足感，散发着数学理性思考的气息。]

（三）不同的推理，拓展思维

生我有个不同的方法。（出示图4）过三角形ABC的顶点A作BC的平行线，则有∠B=∠1，∠C=∠2，这样三角形的三个内角都聚到上面去了，变成了一个平角，所以三角形的内角和就是180°。

生你这个方法和昨天的撕下三个角再拼成一个平角的方法差不多。

生昨天撕和拼的方法会有误差，我们看着像一个平角，实际上是不是平角不能确定。我这里过A点画的是一条直线，那么一定是一个平角。

生你怎么知道∠B=∠1，∠C=∠2的呢？

生我在课外学习知道了内错角，∠B和∠1是内错角，∠C和∠2也是内错角，平行线间的内错角是相等的。

（学生鼓掌。）

师太厉害！用到了初中的内错角知识来证明三角形的内角和是180°。还需要再画一个钝角三角形来说明一下吗？

生没有必要。任何一个三角形，我们总是可以过它的一个顶点画平行线的。

生我也有一个方法来证明三角形的内角和是180°，但是需要大家进行想象。（出示图5）先画个三角形ABC，然后我们把A点往下压，下面的两个角变小了，上面的顶角变大了。继续往下压，下面的两个角就越来越小，越接近0;上面的顶角越来越大，越接近平角，所以三角形的内角和是180°。

师这位同学带着我们通过想象，不停地把顶点A往下压，从而发现三角形的内角和是180°。太了不起了！其实，这里运用了一种极限思想——无限逼近的方法。

[教学意图：展示不同学生的推理方法，一方面，让学生大开眼界：别的同学的方法和自己的完全不同，原来还可以这样推理证明，课外学到的知识也可以帮助我们学习，极限思想的运用，等等;另一方面，也打开了学生思维的大门。]

（四）对比思维方式，感受不同

师今天同学们证明三角形内角和的方法，和昨天的方法有什么不同？

生昨天我们是量（撕、拼）一个个具体的三角形内角的度数，然后计算得出的，今天我们没有研究具体哪一个三角形。

生昨天，我们是做的实验，得出三角形的内角和是180°。今天我们没有做实验，就是在想办法证明。

生昨天，我们量的或者撕和拼的，都会有误差，有的没有到180°，有的比180°又多了些，今天不存在误差。

师是呀，昨天和今天虽然都是在研究三角形的内角和，但我们用了两种不同的思维方式。昨天，我们是通过具体的三角形的例子，实验、归纳得出了三角形的内角和是180°。今天，我们是用知道的一些知识，通过推理得出了三角形的内角和是180°。

师回想一下，上个单元学习的运算律，加法和乘法的那些规律我们是怎么得出的？

生我们在很多很多的算式例子中归纳得出来的。

师是的。比如乘法分配律（a+b）c=ac+bc，我们在大量的算式中找相同之处，同时又找不到反例，最后归纳出了乘法分配律。归纳法可以给我们带来新的发现。其实，乘法分配律也可以用今天的思维方式去证明它，去证明（a+b）c是不是一定等于ac+bc。

（学生跃跃欲试，但是摸不着头绪。）

师可以从乘法和加法之间的关系去证明，a+b乘以c表示什么意思呢？

生c个a+b相加。

师把它写下来：a+b+a+b+…+a+b。

（有几个学生恍然大悟，拿起了笔。）

[教学意图：对比两节课三角形内角和的学习过程，感受不同的思维方式：实验归纳法和演绎推理法，从探索走向论证。同时，给学生提供上个单元才学过的乘法分配律来“操练”推理论证的方法。演绎推理不止于三角形的内角和，也不止于下课的铃声，学生的思维已然打开……]

三、课后反思

（一）纵向延展，要遵循学生的认知规律，准确定位

观察、操作、实验是小学生喜欢的学习方式，所以，“三角形的内角和”这一学习内容向来颇受学生喜欢，学生在量、撕、拼等热闹而忙碌的学习活动中可以轻而易举地得出“三角形内角和是180°”的结论。那么，学生除了得到这个结论外，还会有哪些收获呢？可能是对这个结论的怀疑。课堂上，有不少“聪明”的学生在量角度计算的时候，第三个角的度数不是量出来的，而是算出来的，就为了去凑180°。他们知道大部分测量都会存在误差，但为了得到结果的正确，而去弄虚作假，丢失了实事求是的科学态度。

疑虑，最好是让学生自己去消除。消除疑虑，一般就要进行数学证明。运用数学公理、定理的严谨的数学证明，显然超越了四年级学生的认知发展水平。那就换个思维方式，用推理的方法去证实三角形的内角和为180°，培养和发展初步的论证意识和推理能力，获得证实结论的满足感。从而也满足学生的好奇心：什么是证明？怎样证明？至于实事求是的态度，理性思考的精神，敢于质疑的勇气，科学探究的方法等，则是更为上位的教学目标。

（二）纵向延展，要搭建平台，提供支架

小学生天性好奇、多问。学习了三角形的内角和，他们就想到：四边形的内角和是多少度？其他多边形的内角和是多少度？三角形有内角，那会不会有外角呢？如果有外角，外角和会是多少呢？三角形的内角和真是180°吗？三角形的内角和一定是180°吗？……延展式数学学习，就需要为学生在数学纵深处的探秘搭建平台，提供支架。

于是，全班交流时，让想到用长方形来证明的学生先发言，是教师有意而为之：其一，选择这个方法的学生相对较多，易于接受、理解。其二，长方形是学生最熟悉的知识支架，易于表达。其三，用长方形证明直角三角形的内角和后，易于层层推进，经历严密的演绎推理过程。课堂上提供的长方形纸片是教师精心准备的;长方形的对角线把长方形分成两个完全一样的三角形，学生完全是凭着直观和经验得出的，并把它作为已知事实直接运用来论证;通过剪、重叠这一操作过程，能让学生明白，已知的事实也是需要论证的，由此进一步感受推理的严谨性。学生用任意四边形证明方法的意外插入，教师及时抓住这一生成，让學生反思从长方形入手的原因：原来，我们的每一步都是有理由的，我们的直觉也是有理论支撑的。

（三）纵向延展，可促进数学活动经验的提升

数学活动经验是数学素养的重要标志之一。数学活动经验，除了通过观察、动手操作、实验等这些“看得见”的活动积累的经验之外，也包括数学思维上“看不见”的活动所积累的意会、感悟等经验。

比如，对于用任意四边形证明的学生来说，兴致勃勃的讲解、展示遭到了同学们的质疑，相信数学论证的严谨给他烙下了深刻的印象;对于全班学生来说，到了五年级，研究圆的面积推导时，一定会想起在四年级时就曾有同学运用过极限思想;到了初中，再次学习三角形内角和的证明时，小学一位同学的内错角证明方法可能会在脑海中若隐若现。