非等长Arnold变换与Gray码相融合的图像加密算法

张 帅，杨雪霞

(1.太原广播电视大学 教学研究中心,山西 太原 030024；2.太原科技大学 应用科学学院,山西 太原 030024)

0 引言

图像的加密算法常采用两种方式，一种是对通过位置变换达到降低像素间关联性的目的，常见算法有Arnold变换、Hilbert曲线变换、幻方变换等[1,2].第二种是通过像素值的改变达到图像加密的目的，常见的算法有Gray码置乱、混沌加密等[3].Arnold变换是最常用的图像置乱算法之一，在图像加密预处理中被广泛应用，但仅能对方阵图像进行置乱缺少了应用的普遍性.

文献[4]给出了非等长Arnold变换的公式，证明了当图像长宽比为整数或者互质时周期性的存在.文献[5]在非等长Arnold变换公式的基础上给出了当图像宽与长的比为奇数时也满足周期性.文献[6]根据非等长Arnold变换公式，给出了其逆变换公式，避免了在图像解密过程中要先求解周期的问题，并且通过构造系数矩阵将该公式推广到任意尺寸的变换.文献[7]对图像进行分块处理，分别对方阵和非方阵的图像进行等长与非等长Arnold置乱加密处理.文献[8]对传统的方阵图像进行Arnold变换并结合了Gray变换，对图像进行了双重加密.文献[9]对方阵图像利用Kent混沌映射对图像进行置乱并结合广义的Gray码变换对图像的信息进行了加密处理.

本文提出了一种利用非等长Arnold置乱与Gray码相结合的算法，首先对任意尺寸的载体图像进行非等长Arnold变换，然后对图像的灰度值进行置乱广义Gray码变换，通过双重变换达到了对图像加密的目的.实验结果表明该算法在图像加密过程中表现出更好的安全性.

1 理论知识

1.1 非等长Arnold变换

非等长Arnold变换是针对任意尺寸载体图像进行的研究，具体公式如下：

(1)

为了保证公式(1)能够应用于图像置乱，基本思路是要保证原始载体图像中的两点不能对应于置乱后的同一点.文献[4-6]分别从载体图像的长、宽与系数矩阵两个角度对非等长Arnold变换公式的周期性进行了研究，为了保证变换公式具有普遍性，即能够应用于任意尺寸的载体图像，我们对系数矩阵进行了约束，要求a=1,b>0,c=KN(gcd(M,N))-1,d=1+bc.其中b，k为整数.根据系数矩阵的约束条件，公式1等价为：

(2)

为了避免在图像还原过程中，还需要计算置乱图像的周期性，我们根据公式2给出了逆变换公式，具体形式如下：

(3)

1.2 Gray码变换

定义1任意自然数u，二进制码可以表示为(un-1un-2…u1u0)2，令

gn-1=un-1,gi=ui⊕ui+1.

(4)

其中，i=1,2，…，n-2， 通过计算得，g(u)=(gn-1gn-2…g1g0)2则称g(u)为u的二进制Gray码变换.对公式进行分析，变换过程中最高位进行了直接赋值，因此当图像的灰度值通过Gray码变换以后，灰度值发生了一定的变化，但是由于最高位二进制码保持运算不变，因此灰度值变化幅度并不大，于是我们对公式进行改进提出了广义置乱Gray的表达式.具体定义如下：

定义2任意自然数u，二进制码可以表示为(un-1un-2…u1u0)2，令

(5)

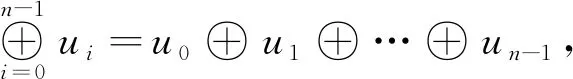
由定义2可知，置乱广义Gray码存在可逆变换，具体表达形式如下：

(6)

其中，i=1,2，…，n-2.自然码、Gray码与置乱广义Gray码变换如表1所示.

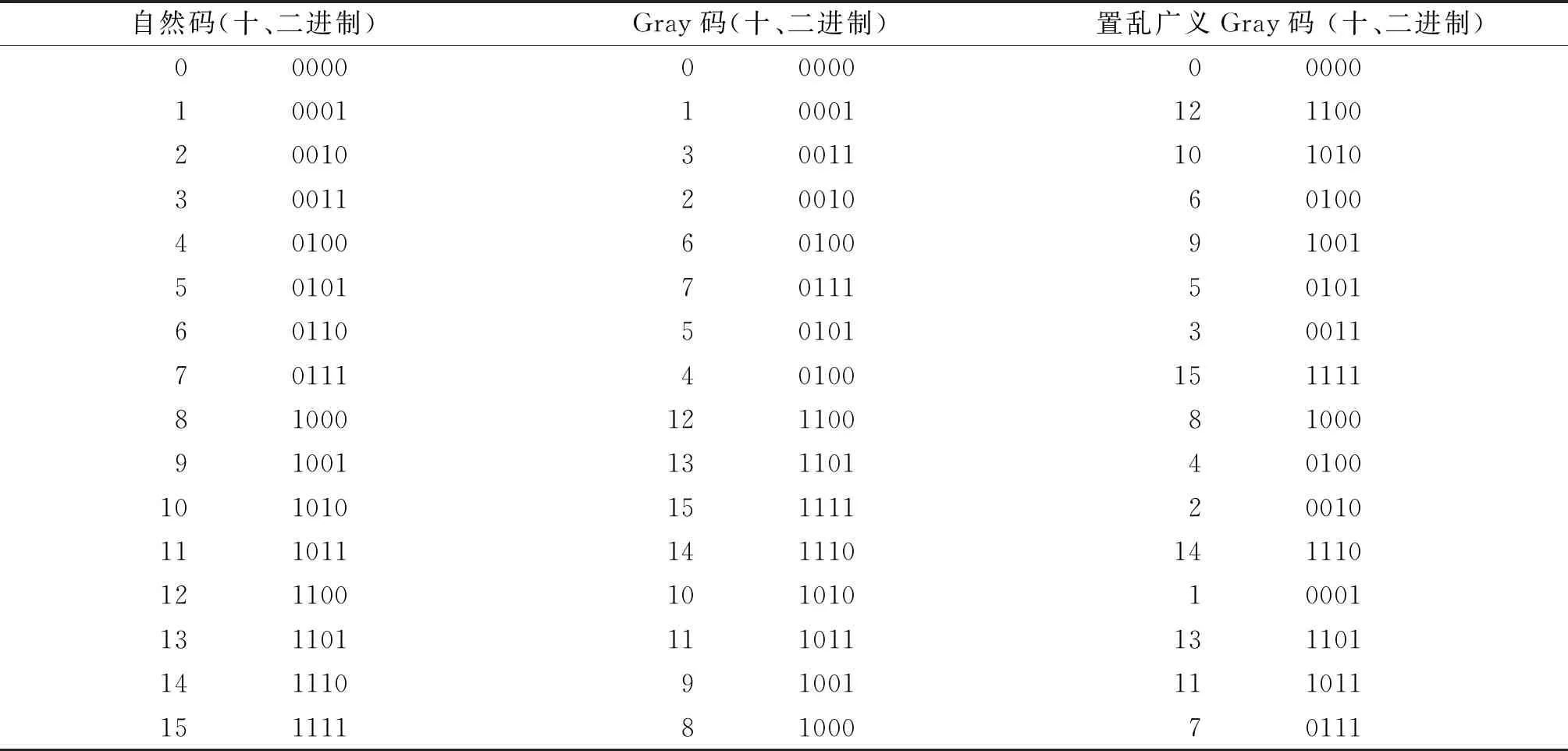
表1 Gray码和置乱广义Gray变换对照表

在表1我们分别给出了十进制和二进制的表示形式，通过分析可知，经过Gray码变换以后，数值仍然基本符合从小到大变换的规律，并且数值变化幅度不大，而经过置乱广义Gray码变换后，数值变换较大，分布离散，更能符合灰度值置乱的要求.

2 算法设计及仿真实验

2.1 算法原理

本算法结合了非等长Arnold变换与置乱广义Gray码的特点，首先对非等长载体图像进行位置变换，然后再利用Gray码变换改变其灰度值，最后根据相应的逆变换公式对图像进行还原.本算法加密与解密的原理如图1所示.

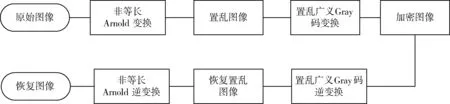
图1 加密与解密流程图

2.2 仿真实验

本文选择大小为248×504的非方阵图像进行研究，根据系数矩阵约束条件，我们取b=5，k=1，结合载体图像的具体尺寸，经计算得c=63，d=316.置乱效果如2所示.

图2 非等长Arnold置乱图像

如图2所示，经过非等长Arnold变换迭代1次与10次，置乱图像与原始图像对比，图像被完全打乱，纹理逐渐变细腻，曾现出杂乱无章的效果.我们从像素相关性的角度作进一步分析，分别在原始图像和迭代10次的置乱图像中选取5 000对像素点，具体结果如图3所示.

由图3(a)可知，原始图像相邻像素点关系表现出良好的线性相关性，经过水平置乱以后，图像像素点的分布表现为离散与随机性，置乱效果显著.虽然图像达到了很好的置乱效果，但由于非等长Arnold 变换仅改变了像素位置，像素的灰度值并没有发生变换，解密仍然可以从其灰度值直方图分布以及置乱的周期性角度进行研究，因此本文在非等长Arnold置乱的基础上结合Gray码变换，改变像素的灰度值，进一步提高图像的加密水平，具体结果如图4所示.

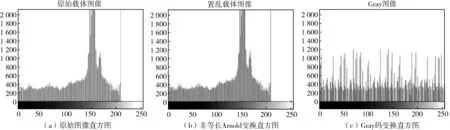
图4 原始图像与置乱图像直方图的相关性

由图4可知，原始图像经过非等长Arnold置乱以后，其灰度值直方图并没有发生变换，经过置乱广义Gray码变换以后，不仅灰度值发生了变换，而且分布更加均匀，因此经过非等长Arnold变换并结合置乱广义Gray码变换以后，不仅打破了像素点之间的关联性而且改变了灰度值的统计特性，使得加密算法有更好的安全性.

最后我们选取5 000对像素点，对经过非等长Arnold变换与置乱广义Gray码双重加密以后图像通过相关系数进行分析，具体公式如下：

(7)

(8)

其中，cov(x,y)表示协方差，rx,y表示相关系数.相关性我们分别从水平、垂直和对角线三个方向进行，并与参考文献进行对比分析.

表2 加密相关性系数对比

对表2分析可知，与原始图像相比加密后图像的相关性趋于0，即像素间几乎不存在相关性，与文献[7,11]仅使用Arnold算法的方法做对比，其相关性更低，因此结合Gray码变换以后本算法达到了更好的加密效果.

3 结论

本文提出了一种非等长Arnold变换与置乱广义Gray码变换相结合的算法，该算法的特点是不仅实现了任意尺寸载体图像的灰度值位置变换，而且结合Gray码变换后实现了灰度值的变化，达到了对图像双重加密的效果，实验结果表明，该算法比传统的仅适用Arnold置乱算法具有更好的加密效果，因此在图像加密预处理过程中具备更好的安全性.